Вывод формулы для напряжений при растяжении

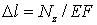
Рассмотрим стержень, нагруженный в точке сечения с координатами xF, yF силой F, параллельной продольной оси z.

Это случай внецентренного сжатия.

В сечениях стержня возникают следующие внутренние силовые факторы:

; ; .

Суммарное нормальное напряжение от действия этих факторов возникает в точке сечения с координатами x, y:

С целью нахождения опасных точек сечения определим положение нейтральной линии, для этого приравняем напряжение, возникающее в точках нейтральной линии, к нулю:

откуда уравнение нейтральной линии имеет следующий вид:

где , — радиусы инерции сечения.

Определим длины отрезков, отсекаемых нейтральной линией на осях координат:

Þ,

Þ.

Условия прочности при внецентренном растяжении-сжатии:

, .

Аналогично данному виду деформации ведется расчет на прочность элементов конструкции, работающих при совместном действии изгиба и растяжения-сжатия.

Вывод формулы Эйлера для определения критической силы.

Для нахождения критических напряжений надо вычислить критическую силу , т. е. наименьшую осевую сжимающую силу, способную удержать в равновесии слегка искривленный сжатый стержень.

Эту задачу впервые решил академик Петербургской Академии наук Л. Эйлер в 1744 году.

Заметим, что самая постановка задачи иная, чем во всех ранее рассмотренных отделах курса. Если раньше мы определяли деформацию стержня при заданных внешних нагрузках, то здесь ставится обратная задача: задавшись искривлением оси сжатого стержня, следует определить, при каком значении осевой сжимающей силы Р такое искривление возможно.

Рассмотрим прямой стержень постоянного сечения, шарнирно опертый по концам; одна из опор допускает возможность продольного перемещения соответствующего конца стержня (рис.3). Собственным весом стержня пренебрегаем.

Рис.3. Расчетная схема в «задаче Эйлера»

Нагрузим стержень центрально приложенными продольными сжимающими силами и дадим ему весьма небольшое искривление в плоскости наименьшей жесткости; стержень удерживается в искривленном состоянии, что возможно, так как .

Деформация изгиба стержня предположена весьма малой, поэтому для решения поставленной задачи можно воспользоваться приближенным дифференциальным уравнением изогнутой оси стержня. Выбрав начало координат в точкеА и направление координатных осей, как показано на рис.3, имеем:

(1)

Возьмем сечение на расстоянии х от начала координат; ордината изогнутой оси в этом сечении будет у, а изгибающий момент равен

По исходной схеме изгибающий момент получается отрицательным, ординаты же при выбранном направлении оси у оказываются положительными. (Если бы стержень искривился выпуклостью книзу, то момент был бы положительным, а у — отрицательным и .)

Приведенное только что дифференциальное уравнение принимает вид:

деля обе части уравнения на EJ и обозначая дробь через приводим его к виду:

Общий интеграл этого уравнения имеет вид:

Это решение заключает в себе три неизвестных: постоянные интегрирования а и b и значение , так как величина критической силы нам неизвестна.

Краевые условия на концах стержня дают два уравнения:

в точке А при х = 0 прогиб у = 0,

В х = 1 у = 0.

Из первого условия следует (так как и coskx =1)

0 = b.

Таким образом, изогнутая ось является синусоидой с уравнением

(2)

Применяя второе условие, подставляем в это уравнение

у = 0 и х = l

получаем:

Отсюда следует, что или а или klравны нулю.

Еслиа равно нулю, то из уравнения (2) следует, что прогиб в любом сечении стержня равен нулю, т. е. стержень остался прямым. Это противоречит исходным предпосылкам нашего вывода. Следовательно, sinkl = 0, и величина может иметь следующий бесконечный ряд значений:

где — любое целое число.

Отсюда , а так как то

Иначе говоря, нагрузка, способная удержать слегка искривленный стержень в равновесии, теоретически может иметь целый ряд значений. Но так как отыскивается, и интересно с практической точки зрения, наименьшее значение осевой сжимающей силы, при которой становится возможным продольный изгиб, то следует принять .

Первый корень =0 требует, чтобы было равно нулю, что не отвечает исходным данным задачи; поэтому этот корень должен быть отброшен и наименьшим корнем принимается значение . Тогда получаем выражение для критической силы:

Источник

Вывод формул для определения напряжений и перемещений при растяжении (сжатии) прямого стержня

Напомним, что под растяжением (сжатием) понимают такой вид деформации стержня, при котором в его поперечном сечении возникает лишь один внутренний силовой фактор — продольная сила Nz. Поскольку продольная сила численно равна сумме проекций, приложенных к одной из отсеченных частей внешних сил на ось стержня (для прямолинейного стержня она совпадает в каждом сечении с осью Oz), то растяжение (сжатие) имеет место, если все внешние силы, действующие по одну сторону от данного поперечного сечения, сводятся к равнодействующей, направленной вдоль оси стержня (рис. 1). Одна и та же продольная сила Nz при действии на различные части стержня (левую или правую) имеет противоположные направления. Знак Nz зависит от характера вызываемой ею деформации. Продольная сила считается положительной, если вызывает растяжение элемента (рис. 2, а), и она отрицательна, если вызывает сжатие.

Поскольку поперечные сечения стержня, оставаясь плоскими и перпендикулярными к оси стержня, в процессе деформирования лишь поступательно перемещаются вдоль оси стержня (что приводит к одинаковому удлинению всех продольных волокон), то приходим к уравнению =const, из которого ввиду однозначности связи и (для линейно-упругого материала это—закон Гука: .) вытекает, что

Решая совместно уравнения получим, что или

Таким образом, при растяжении (сжатии) призматического стержня нормальные напряжения равномерно распределены по поперечному сечению, а касательные напряжения в сечениях отсутствуют, что является следствием гипотезы плоских сечений. Указанное, несмотря на, казалось бы, очевидность и простоту, является фундаментальным результатом, справедливым, строго говоря, лишь для призматического стержня. Однако в инженерной практике его используют и для приближенной оценки нормальных напряжений в стержнях переменного сечения. При этом, чтобы погрешность формулы была невелика, необходимо, чтобы площадь поперечного сечения стержня изменялась достаточно плавно вдоль его оси.

Условие прочности при растяжении (сжатии) призматического стержня для стержня из пластического материала (т. е. материала, одинаково работающего на растяжение и сжатие) будет иметь вид:

(1)

где —допускаемое напряжение. Напряжение в условии (1) подставляется по модулю, так как знак в этом случае роли не играет. Для стержней из хрупких материалов, неодинаково сопротивляющихся растяжению и сжатию, знак напряжения имеет принципиальное значение, и условие прочности приходится формулировать отдельно для растяжения и сжатия

где и —напряжения растяжения и сжатия, а и — ответствующие им допускаемые напряжения.

Определим упругие деформации стержня предполагая, что изменение его длины при растяжении , называемое абсолютной продольной деформацией или удлинением, мало по сравнению с его первоначальной длиной . Тогда относительная продольная деформация будет равна

Учитывая, что согласно закону Гука для одноосного растяжения (сжатия)

где Е—;модуль продольной упругости материала стержня, а нормальные напряжения определяются по формуле — (в нашем случае Nz=P), для абсолютной деформации получаем

(2)

Произведение EF принято называть жесткостью поперечного сечения стержня при растяжении (сжатии), так как удлинение обратно пропорционально EF.

Рис.6. Модели продольной и поперечной деформаций

Как показывают эксперименты, при растяжении стержня размеры его поперечного сечения уменьшаются (рис. 6), а при сжатии — увеличиваются. Это явление получило название эффекта Пуассона.

По аналогии с продольной деформацией изменение размеров поперечного сечения (на рис. 6 ) будем называть абсолютной поперечной деформацией, а — относительной поперечной деформацией. Относительные продольная и поперечная деформации, имеющие противоположные знаки, связаны между собой коэффициентом , являющимся константой материала и называемым коэффициентом поперечной деформации или коэффициентом Пуассона:

Как известно, для изотропного материала .

Формула (2) для удлинения стержня применима только в случае, когда по длине стержня ни жесткость поперечного сечения, ни продольная сила не изменяются (EF=const, Nz =const). Удлинение стержня со ступенчатым изменением EF и Nz (рис. 7) может быть определено как сумма удлинений ступеней, у которых EF и Nz постоянны:

(индекс k у модуля продольной упругости означает, что участки стержня могут быть изготовлены из различных материалов). В случае, когда Nz и EF меняются по длине стержня l непрерывно и их можно считать постоянными лишь в пределах ступеней длиной dz, обобщая формулу эту, получаем

Источник

При растяжении и сжатии в сечении действует только нормальное напряжение. Напряжения в поперечных сечениях могут рассматриваться как силы, приходящиеся на единицу площади. Таким образом, направление и знак напряжения в сечении совпадают с направлением и знаком силы в сечении (рис.32.).

Исходя из гипотезы плоских сечений, можно предположить, что напряжение при растяжении и сжатии в пределах каждого сечения не меняются. По этому напряжение можно рассчитать по формуле:

где Nz — продольная сила; А — площадь поперечного сечения.

Величина напряжения прямо пропорциональна продольной силе и обратно пропорциональна площади поперечного сечения.

Нормальные напряжения действуют при растяжении от сечения (рис. 33а), а при сжатии к сечению (рис. 336).

Размерность (единица измерения) напряжений — (Па), однако это слишком малая единица, и практически напряжения рассчитывают в
При определении напряжений брус разбивают На участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений. Рассчитывают напряжения по сечениям, и расчёт оформляют в виде эпюры нормальных напряжений.

Строится и оформляется такая же эпюра, как и эпюра продольных сил.

Пусть в результате деформации первоначальная длина стержня l станет равной. l1. Изменение длины

называется абсолютным удлинением стержня.

Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением ( – эпсилон) или продольной деформацией. Продольная деформация – это безразмерная величина. Формула безразмерной деформации:

При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.

Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:

Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона иликоэффициентом поперечной деформации, вычисляется по формуле:

Для различных материалов коэффициент Пуассона изменяется в пределах . Например, для пробки , для каучука , для стали , для золота .

5. Определение перемещений в стержне при растяжении-сжатии.

При растяжении — сжатии относительная продольная деформация в каждой

точке поперечного сечения стержня одна и та же и определяется как

где и — продольное перемещение поперечного сечения. Из

данного равенства du = zdx. Интегрируя его

(10)

где м0 — перемещение начального поперечного сечения стержня; и — перемещение рассматриваемого поперечного сечения, положение которого определяется координатой х ; л:0- координата начального поперечного сечения.

По закону Гука при растяжении-сжатии где Е — модуль упругости

1-го рода материала стержня. Обозначим — изменение длины

стержня для рассматриваемого поперечного сечения. Тогда (10) примет вид

Если свойства материала по длине стержня не изменяются и Е const, то

. (12)

Функция нормальных напряжений а, как правило, имеет разрывы при переходе с одного участка на другой (рис.7,6) и непрерывна в пределах каждого участка. Поэтому, если рассматриваемое сечение (рис. 7,в) находится в пределах первого участка 0<х<а (0<Jtj < я), то изменение длины стержня

в данном поперечном сечении равно (учитываем, что а, = const)

Если рассматриваемое сечение (рис. 7,г) находится в пределах 2-го участка , то изменение длины стержня в данном поперечном сечении равно (учитываем, что ст2 ~ const)

(14)

6. Диаграмма растяжения и механические характеристики материала.

Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.

Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).

Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.

Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.

На рис. 1 показана диаграмма для малоуглеродистой стали. Она построена в системе координат F-Δl, где:

F — продольная растягивающая сила, [Н];

Δl — абсолютное удлинение рабочей части образца, [мм]

Рис. 1 Диаграмма растяжения стального образца

Как видно из рисунка, диаграмма имеет четыре характерных участка:

I — участок пропорциональности;

II — участок текучести;

III — участок самоупрочнения;

IV — участок разрушения.

Рассмотрим подробнее процесс построения диаграммы.

В самом начале испытания на растяжение, растягивающая сила F, а следовательно, и деформация Δl стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О).

На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня Δl растут пропорционально увеличивающейся нагрузке F.

После прохождения точки А диаграмма резко меняет свое направление и на участке II начинающемся в точке B линия какое-то время идет практически параллельно оси Δl, то есть деформации стержня увеличиваются при практически одном и том же значении нагрузки.

В этот момент в металле образца начинают происходить необратимые изменения. Перестраивается кристаллическая решетка металла. При этом наблюдается эффект его самоупрочнения.

После повышения прочности материала образца, диаграмма снова «идет вверх» (участок III) и в точке D растягивающее усилие достигает максимального значения. В этот момент в рабочей части испытуемого образца появляется локальное утоньшение (рис. 2), так называемая «шейка», вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).

Рис. 2 Стальной образец с «шейкой»

Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения образца, растягиваещее усилие необходимое для его растяжения уменьшается, и кривая диаграммы «идет вниз».

В точке E происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована «шейка»

Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:

W=0,8Fmax⋅Δlmax

По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.

Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.

8. Понятия о допускаемых напряжениях и деформациях при растяжении и сжатии. Условия прочности и жёсткости. Три вида расчетов на прочность и жесткость.

Допускаемые напряжения – это наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы.

Как показывают механические испытания (испытания на растяжение и сжатие), разрушение хрупких материалов начинается, когда напряжения в сечении элемента конструкции превысят величину временного сопротивления (предела прочности) σв. Поэтому для хрупких материалов, деформация которых, как правило, незначительна, за опасное (предельное) напряжение следует принимать именно предел прочности σв:

σо = σв.

Для пластичных материалов за опасное (предельное) напряжение следует принимать предел текучести σт (или условный предел текучести σ0,2, если площадка текучести отсутствует), так как за пределом текучести в пластичных материалах возникают значительные пластические деформации, приводящие при сбросе нагрузки до нуля к появлению остаточных напряжений, следовательно:

σо = σт .

Естественно, что эти опасные напряжения не могут быть использованы в качестве допускаемых. Их следует уменьшить настолько, чтобы в эксплуатационных условиях действующие напряжения гарантированно были меньше опасных, а деформации были упругими. Таким образом, допускаемое напряжение может быть определено по формуле σо

где σо – опасное напряжение; n – коэффициент запаса прочности.

Рассмотрим условия прочности и жесткости для случаев простого растяжения (сжатия). Опасность наступления разрушения характеризуется величинами наибольших нормальных и касательных напряжений, возникающих при нагружении в опасных (т. е. наиболее напряженных) точках сечения. Очевидно, что реальные материалы не могут выдерживать сколь угодно большие напряжения. Поэтому величины наибольших напряжений из условия надежности работы детали необходимо ограничивать некоторыми допустимыми значениями, такими, чтобы деталь испытывала только упругие деформации. Их называют допускаемыми напряжениями. При растяжении и сжатии допускаемые напряжения обозначают [σ+], [σ–] соответственно (принято также обозначение σadm).

Если из расчета известны максимальные и минимальные (по алгебраической величине) напряжения, возникающие в опасном сечении детали, то условия прочности могут быть записаны следующим образом:

Если материал одинаково сопротивляется растяжению и сжатию, что характерно для пластичных материалов (более строго–для материалов в пластичном состоянии), а значит [σ+]=[σ–]=[σ], то

иусловие прочности при растяжении (сжатии) запишем в виде:

В некоторых случаях для обеспечения нормальной работы машин и сооружений размеры их деталей нужно выбирать так, чтобы обеспечивалось условие жесткости, то есть ограничить предельные деформации (перемещения) элементов конструкции.

Условие жесткости, ограничивающее изменение длины элемента, имеет следующий общий вид:

где∆l – изменение размеров детали; [∆l] – допускаемая величина этого изменения.

Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин ∆l по участкам

условие жесткости при растяжении (сжатии) запишем следующим образом:

Используя условие прочности, можно решать три типа задач:

1) проектировочный расчет – по известным нагрузкам для известного материала найти надежные с точки зрения прочности размеры поперечного сечения стержня (спроектировать прочную деталь);

2) проверочный расчет – по заданным размерам и материалу детали проверить, может ли она выдержать приложенную нагрузку;

3) расчет по несущей способности (грузоподъемности) – по известным размерам детали, материалу и схеме нагружения определить допустимую величину нагрузки на деталь.

9. Напряжения и деформации при сдвиге. Условие прочности.

Сдвиг (срез) – вид деформации, при котором одна часть стержня смещается относительно другой (скользит). Сдвиг, как вид нагружения, встречается редко и имеет место в заклепочных и сварных соединениях. Деформация сдвига происходит в случае, если к стержню приложены две равные по модулю противоположно направленные силы P , перпендикулярные к его продольной оси. Расстояние между этими силами должно быть малым, чтобы можно было пренебречь моментом, создаваемым силами.

Рис. 16. Расчетная схема при сдвиге

Используя метод сечений (разрезая стержень между силами P), можно установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная сила Q.

Такой вид нагружения, при котором в поперечных сечениях стержня действует только поперечная сила, называют чистым сдвигом.

Мера скольжения одного поперечного сечения относительно другого – касательные напряжения τ.

Принято, что касательные напряжения распределены по всей площади поперечного сечения равномерно. Если в поперечном сечении стержня площадью A возникает внутренняя поперечная сила Q = P, то касательные напряжения в любой точке этого сечения будут равны: T = Q/A = P/A.

Рис. 17. Чистый сдвиг

При чистом сдвиге возникает плоское напряженное состояние, тогда напряжения, действующие на площадке составляющей угол α с вертикальной исходной площадкой равны:

Касательные напряжения τ, приведенные на рис. 17, по абсолютной величине больше касательных напряжений по любым другим площадкам. Таким образом, они являются экстремальными, а площадки, по которым они действуют – площадками сдвига. Так как по этим площадкам не действуют нормальные напряжения, то их называют площадками чистого сдвига и они образуют с главными площадками углы, равные 45°.

При чистом сдвиге нормальные напряжения на любых двух взаимно перпендикулярных площадках равны друг другу по модулю и противоположны по направлению.

Касательные напряжения τ измеряются в таких же единицах, что и нормальные напряжения: мегапаскалях, килоньютонах на квадратные сантиметры, килограммах силы на квадратный сантиметр (МПа, кН/см2, кгс/см2) и т.п.

В результате сдвига одно поперечное сечение стержня смещается относительно другого на величину δ, называемую абсолютным сдвигом.

Рис. 18. Углы сдвига

10. Напряженное состояние и закон гука при сдвиге

Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения , где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: s1= — s3 = t; s2= 0. Главные площадки составляют с площадками чистого сдвига угол 45о.

При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. d — абсолютный сдвиг,

g » — относительный сдвиг или угол сдвига.

Закон Гука при сдвиге: g = t/G или t = G×g .

G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, m— коэффициент Пуассона).

Потенциальная энергия при сдвиге: .

Удельная потенциальная энергия деформации при сдвиге: ,

где V=а×F — объем элемента. Учитывая закон Гука, .

Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.

11. Определение напряжений при кручении круглых валов. Условие прочности.

Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряженийи записывается в виде

где — берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:

— из второй теории прочности

— из теории Мора

Из теорий прочности для пластичных материалов при чистом сдвиге получим:

— по третьей теории прочности

— по четвертой теории прочности

Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором , то при повороте граней элемента на 450 в новых площадках обнаруживаются только нормальные напряжения, равные по величине (рис.5.8).

Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис.5.9,а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 450, т.е. по направлению действия максимальных растягивающих напряжений (рис.5.9,б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис.5.9,в).

Рис.5.8 Рис.5.9

Таким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равным — для хрупких материалов и — для пластичных материалов.

12. Определение угла закручивания круглых валов. Условие жесткости.

При определении величины крутящего момента используется метод сечений. Суть его заключается в следующем: рассекаем вал сечением и отбрасываем одну из частей вала, расположенную либо справа, либо слева от сечения.

Обычно отбрасывают ту часть, к которой приложено больше скручивающих пар. Действие отброшенной части на рассматриваемую заменяют внутренним силовым фактором – крутящим моментом T. Затем из условий равновесия остановленной части вала определяют крутящий момент:

T = Мк= Σ Мi . (5.1)

Таким образом, крутящий момент в каком-либо сечении вала является уравновешивающей парой сил всех внешних скручивающих пар, приложенных либо слева, либо справа от рассматриваемого сечения.

Рис. 5.1

Угол сдвига

Максимальное касательное напряжение

Деформации вала

Угол закручивания:

— относительный

— абсолютный

Условие жесткости вала

Расчет вала при кручении сводится к одновременному удовлетворению двух условий:

— условия жесткости:

13. Полярный момент инерции и полярный момент сопротивления для круглого сечения вала.

Геометрические характеристики круглых сплошных сечений вала:

Поля́рный моме́нт ине́рции — интегральная сумма произведений площадей элементарных площадок dA на квадрат расстояния их от полюса — ρ2 (в полярной системе координат), взятая по всей площади сечения. То есть:

— полярный момент инерции

— полярный момент сопротивления

Эта величина используется для прогнозирования способности объекта оказывать сопротивление кручению. Она имеет размерность единиц длины в четвёртой степени (м4, см4) и может быть лишь положительной.

Сама формула выглядит следующим образом:

Для круглого сплошного сечения:

где D — диаметр круга.

Дата добавления: 2016-11-12; просмотров: 8375 | Нарушение авторских прав | Изречения для студентов