Задачи на силу растяжения

Пример решения задачи на растяжение и сжатие
.
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) с размерами см; см, см и площадью поперечного сечения нижнего участка см2, а верхнего – см2 нагружен внешними осевыми силами кН и кН. Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Расчетная схема для задачи на растяжение и сжатие
рис 3.2
Решение пример задачи на растяжение и сжатие
Определяем значение опорной реакции , возникающей в заделке
Учитывая, что , направим опорную реакцию вниз. Тогда из уравнения равновесия находим:
кН.
Строим эпюру продольных сил
Разбиваем длину стержня на три участка. Границами участков являются сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений. Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Cечение 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. 3.2, б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила растягивает рассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила уравновесит внешнюю силу . Поэтому очевидно, что
кН.
Сечение 2 – 2. Внешняя сила растягивает рассматриваемую нами нижнюю часть стержня, а сила ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила , противодействующая сжатию, то есть направленная к сечению. Она равна:
кН.
Сечение 3 – 3. Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила должна уравновесить внешнюю (реактивную) сжимающую силу . Поэтому она направлена к сечению и равна:
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила также противодействует сжатию. Она равна:
кН.
При построении эпюры продольных сил будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию. Оно вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому кН.
Для построения эпюры продольных сил проводим тонкой линией ось, параллельную оси стержня z (рис. 3.2, д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. 3.2, д, никак не сказывается на характере эпюры .
Строим эпюру нормальных напряжений
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
,
где и – продольная сила и площадь k–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
кН/см2,
во втором –
кН/см2,
в третьем –
кН/см2.
Строим по вычисленным значениям эпюру (рис. 3.2, е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
Оцениваем прочность стержня
Сопоставляем наибольшее (по модулю) нормальное напряжение , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением . Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: . Тогда
кН/см2.
Условие прочности имеет вид . В нашем случае
кН/см2 > кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
см2.
Принимаем на втором участке см2.
Вычисляем удлинение всего стержня
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
,
где E – модуль Юнга, а – длина соответствующего участка стержня.
Тогда
см.
Таким образом, длина стержня уменьшается на мм.
Задача по сопромату на растяжение и сжатие для самостоятельного решения
Условие задачи на растяжение и сжатие
Стальной стержень (модуль Юнга кН/см2) находится под действием внешних осевых сил и (рис. 3.1). Построить эпюры продольных сил и нормальных напряжений . Оценить прочность стержня, если предельное напряжение (предел текучести) кН/см2, а допускаемый коэффициент запаса . Найти удлинение стержня .
Схемы для задачи на растяжение и сжатие
Исходные данные к задаче на растяжение и сжатие
Номер схемы | F, см2 | a, м | b, м | c, м | P, кН |
1 | 2,0 | 1,2 | 1,4 | 1,6 | 11 |
2 | 2,2 | 1,4 | 1,6 | 1,4 | 12 |
3 | 2,4 | 1,8 | 1,6 | 1,2 | 13 |
4 | 2,6 | 1,6 | 2,0 | 1,0 | 14 |
5 | 2,8 | 2,0 | 1,8 | 1,2 | 15 |
6 | 3,0 | 2,2 | 1,6 | 1,4 | 16 |
7 | 3,2 | 2,4 | 1,4 | 1,6 | 17 |
8 | 3,4 | 2,6 | 1,2 | 1,8 | 18 |
9 | 3,6 | 2,8 | 1,0 | 1,4 | 19 |
3,8 | 2,4 | 1,6 | 1,2 | 20 |
Источник
Рассмотрим примеры,
связанные с деформациями растяжения
(сжатия), в которых определяются величины,
связанные с нагружением, деформированием
и построением эпюр, характеризующих
процесс.
Пример 1.
ℓ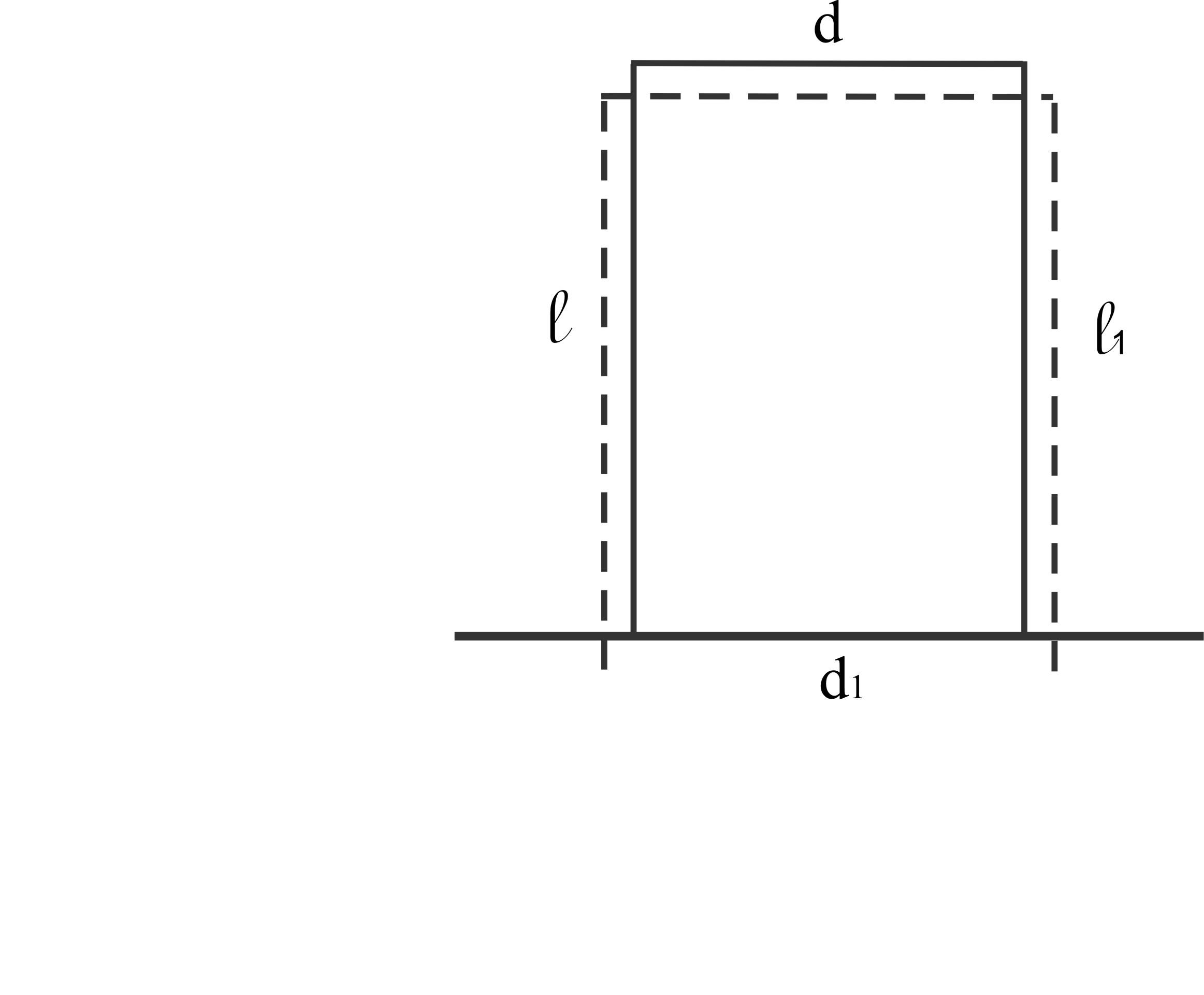
=
100 мм; ℓ1 =
99,9 мм
d
= 40 мм; d1
= 40,01 мм
Найти коэффициент
Пуассона.
Решение:
│ε│
=
![]() ,
,
│ε’│ =
![]()
μ
(ν) =
![]()
=
![]()
= 0,25.
Пример 2.
Подкос ВС квадратного
сечения — дуб
[σ]
= 12 МПа, а = 1м, F
= 10 кН
Определить размер
подкоса.
Решение:
R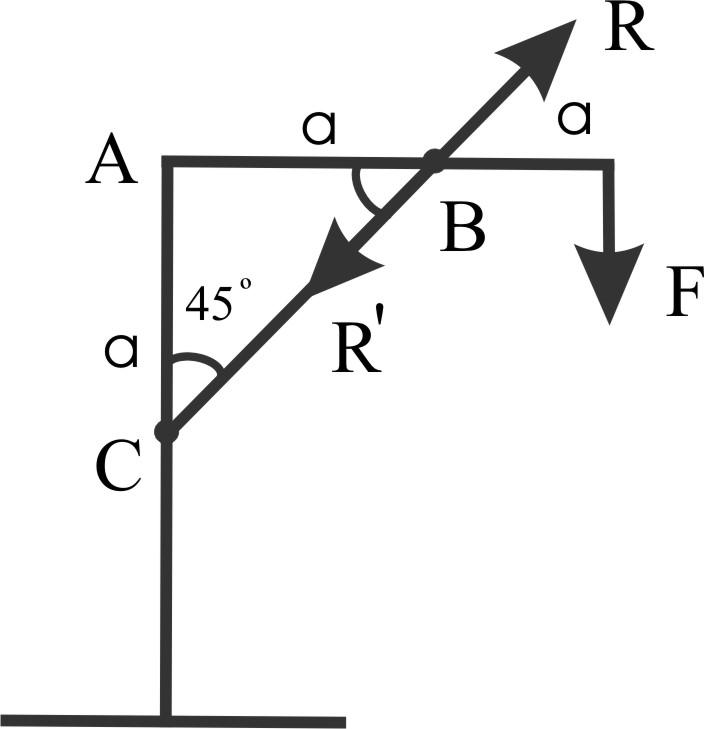
вдоль стержня, подкос испытывает сжатие.
Условие равновесия
определим:
сумма моментов
относительно А
Σ
MA
= с
= — F 2a + R sin45ºa,
откуда
R
=
![]()
=
![]()
= 28,4 кН
Для сжатия расчетное
соотношение:
A
=
![]()
=
![]()
= 2,3710-3
м2
т.к.
квадрат, то B
=
![]()
в
=
![]() ×10-3
×10-3
м = 48,6 мм.
Пример 3.
Стальная
полоса 30×10 мм, ℓ = 250 мм растянута силой
P
= 60 кН;
Е
= 2×105
МПа.
Вычислить:
σ
(нормальное напряжение); ∆ℓ (абсолютное
удлинение);
ε (относительное
удлинение).
Решение:
σ
=
![]()
=
![]()
= 2![]() 108
108
Па = 200 МПа
По закону Гука
ε
=
![]()
=
![]()
![]()
![]()
=
![]()
=
![]()
= 10-3
εℓ
= ∆ℓ =
![]()
=
![]()
![]() ℓ
ℓ
= 10-3×250
мм = 0,25 мм.
Пример 4.
Цилиндрический
стальной стержень ℓ = 40 см и D
= 2 см в средней части ослаблен прорезью
ℓ1
= 20 см и шириной h
= 1 см, растянут силой P
= 15 кН, E
= 2×105
МПа.
Вычислить:
Δℓ
полное; σ
ослабл и σ
неосл.
Решение:
Изобразим условие:
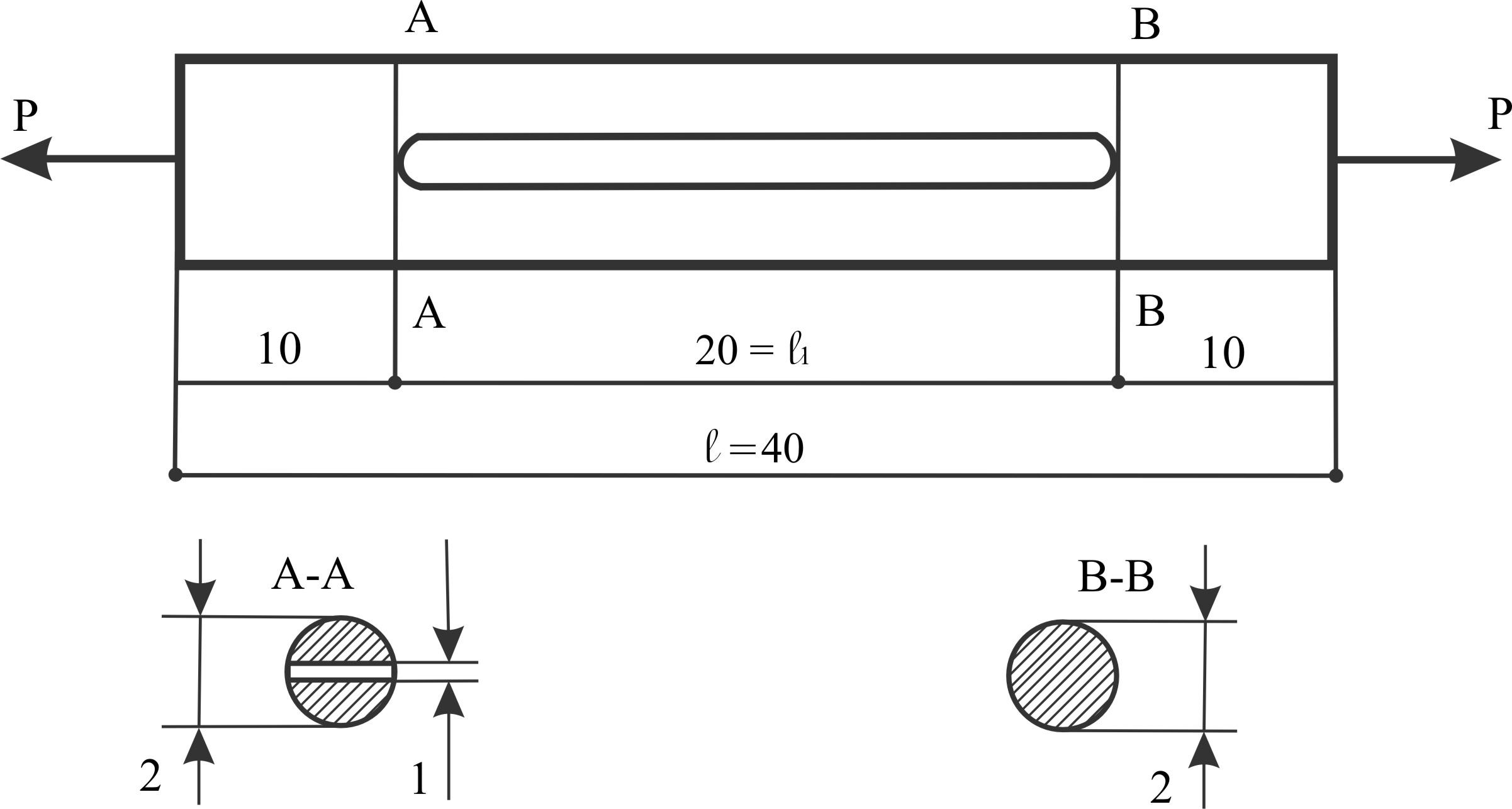
В неослабленных
местах (без прорези)
σ1
=
![]()
=
![]()
=
![]()
Па = 4,77×107
Па = 47,7 МПа.
∆ℓ1
=
![]()
![]() (ℓ
(ℓ
— ℓ1)
=
![]()
= 4,77![]() 10-5
10-5
м = 0,0477 мм.
В
ослабленной части (с прорезью) F2
=
![]()
— Dh.
σ2
=
![]()
=
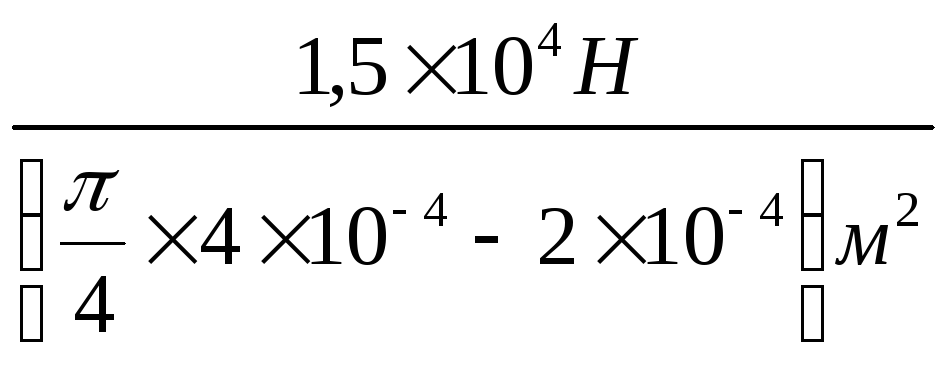
= 1,31![]() 108
108
Па = 131 МПа.
∆ℓ2
=
![]()
![]() ℓ1
ℓ1
=
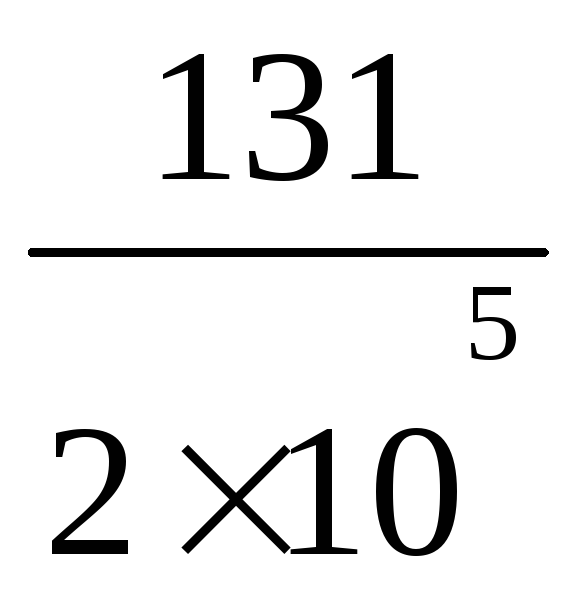
![]() 2
2![]() 10-1
10-1
= 131![]() 10-6м
10-6м
= 0,131 мм.
∆ℓ =
∆ℓ1
+ ∆ℓ2
= 0,1787 мм = 0,18 мм.
Пример
5.
Мачтовый
кран АВ (труба) 20![]() 18
18
мм;
С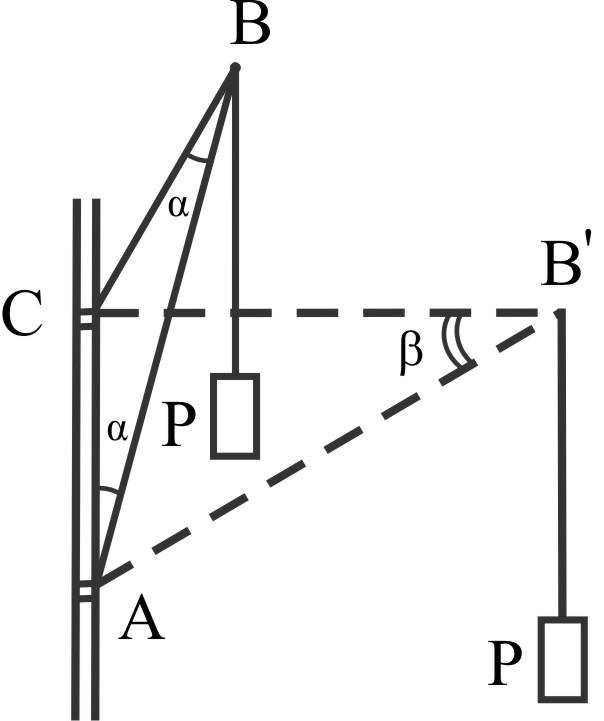 В
В
(трос) FCB
= 0,1 см2
P
= 2кН; α = 15º; β = 30º
∆ABC
→ ∆AB’C
Вычислить
σAB
и σBC.
Найти
— как изменятся напряжения при переводе
крана из ABC
в AB’C
Решение:
Для
разложения P
= (NAB;
NBC)
используем теорему синусов
I.
![]()
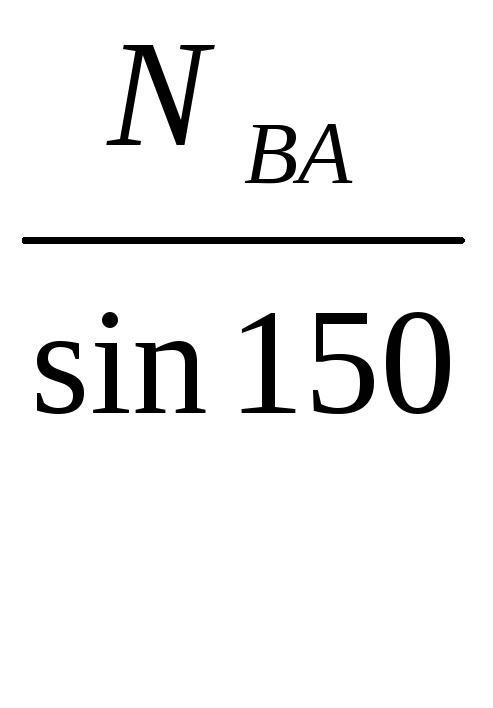
=
![]()
=
![]()
; NBC
= P;
NBA
=
![]()
= —
![]()
= — 1,93 P.
σBA
=
![]()
= —
![]()
= -6,47![]() 107
107
Па = — 64,7 МПа.
σBC
=
![]()
=
![]()
= 200 МПа.
II.
после перевода в новое положение
![]()
![]()
=
![]()
=
![]() ,
,
что дает
NB’A
= 2P,
σB’A
=
![]()
= 67,2 МПа.
NB’C
=
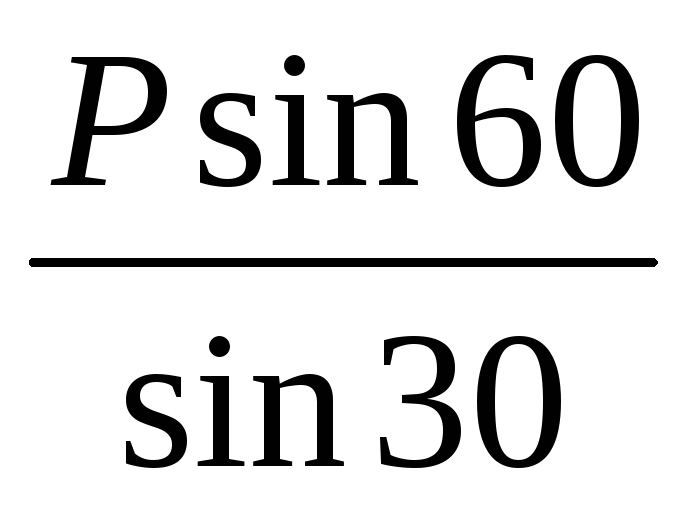
= 2P![]() 0,866;
0,866;
σB’C
= 346,4 МПа.
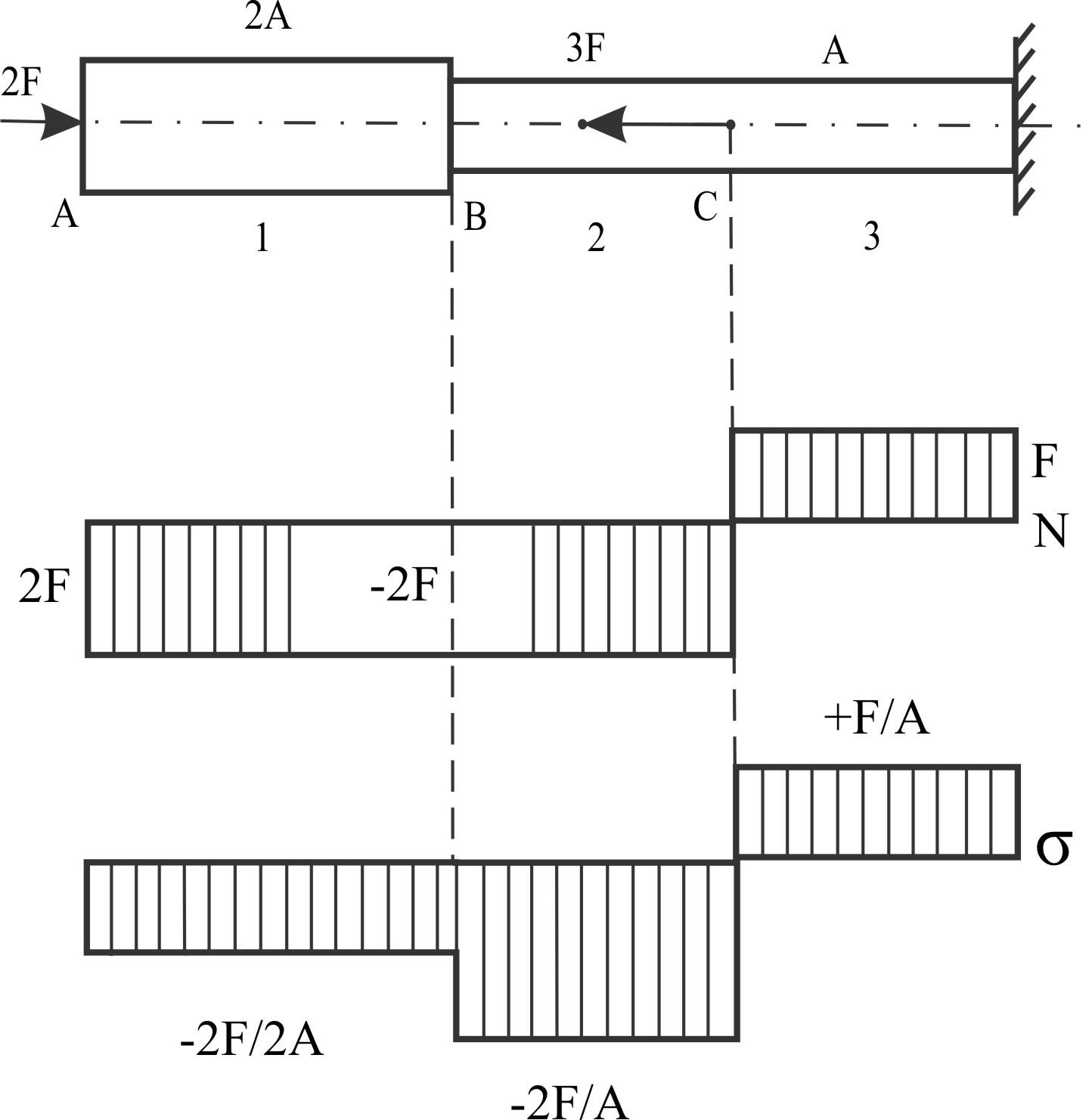
Пример 6.
Ступенчатый брус.
Указаны силы и
сечения на рисунке.
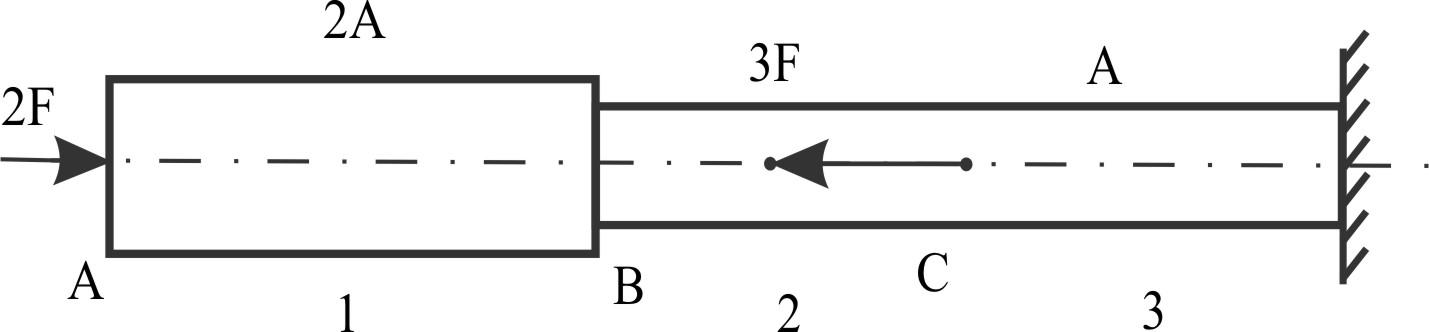
Построить эпюры
сил и напряжений.
Решение:
Строим
от свободного конца: в «C»;
скачок N,
σ
меняется в «B»
за счет изменения сечения; в «C»
за счет скачка силы.
Пример 7.
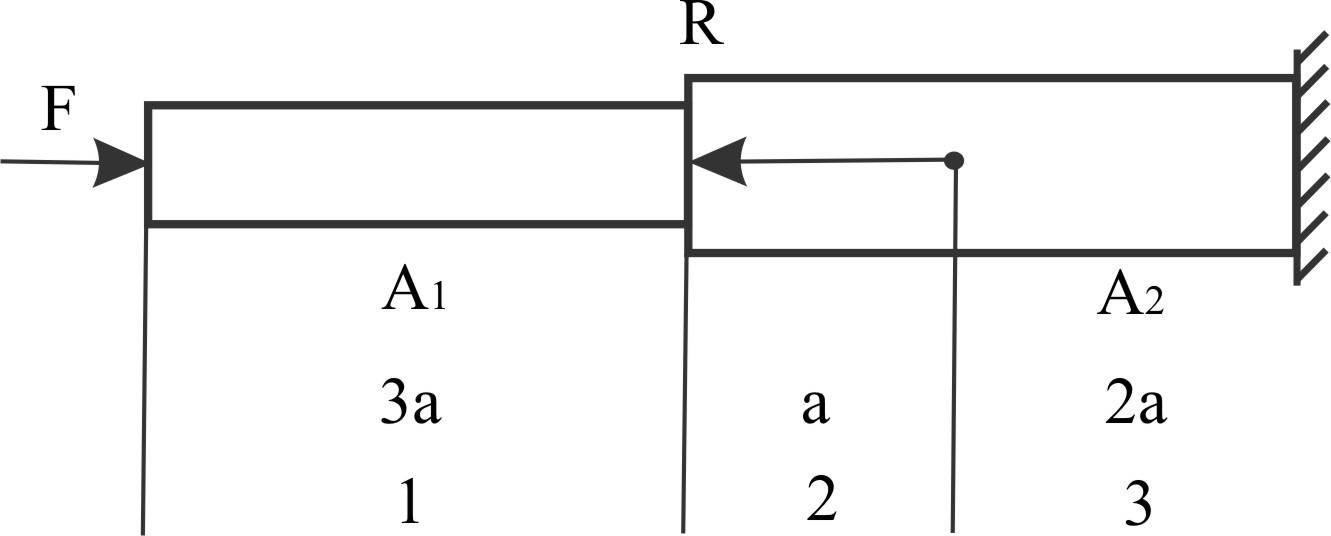
F
= 40 кН, R
= 60 кН
A1
= 800 мм2,
A2
= 1600 мм2
a
= 0,2 м, E
= 2×1011
Па
Определить изменения
длин участков и перемещение свободного
конца.
Решение:
∆ℓ1 | N1 | ∆ℓ1 |
∆ℓ2 | N2 | ∆ℓ2 |
∆ℓ3 | N3 | ∆ℓ3 |
λ
= ∆ℓ1
+ ∆ℓ2
+ ∆ℓ3
= — 0,15 мм.
Весь брус укоротится,
укорочение определится перемещением
свободного конца.
Пример 8.
E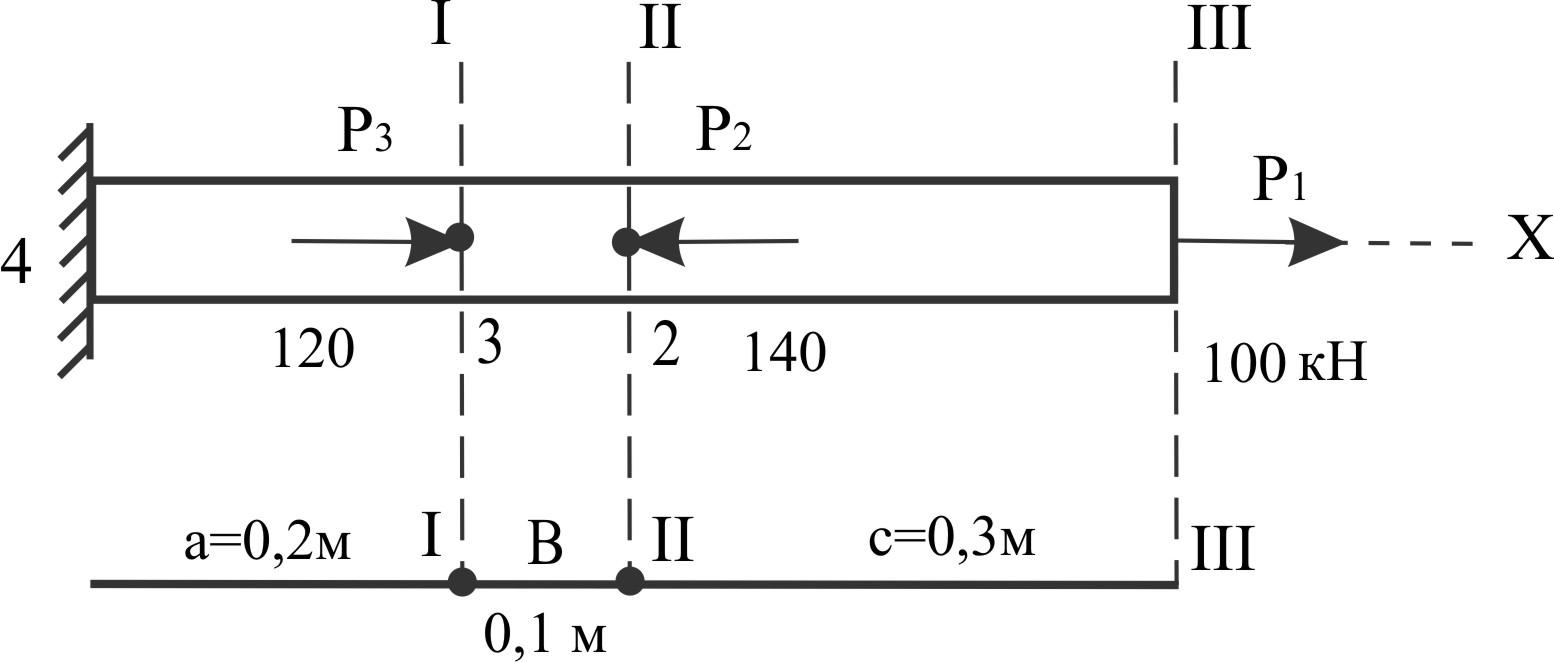
= 2×105
МПа
Ø = 3 см
P1
= 100 кН
P2
= 140 кН
P3
= 120 кН
Вычислить
продольные силы N
и σ
на участках 1-2, 2-3, 3-4; перемещения ω
сечений I-I,
II-II
и III-III;
построить эпюры N,
σ,
ω.
Решение:
Продольные силы
на участках (начиная от свободного
конца) на отдельных участках = Σ всех
сил по одну сторону от сечения.
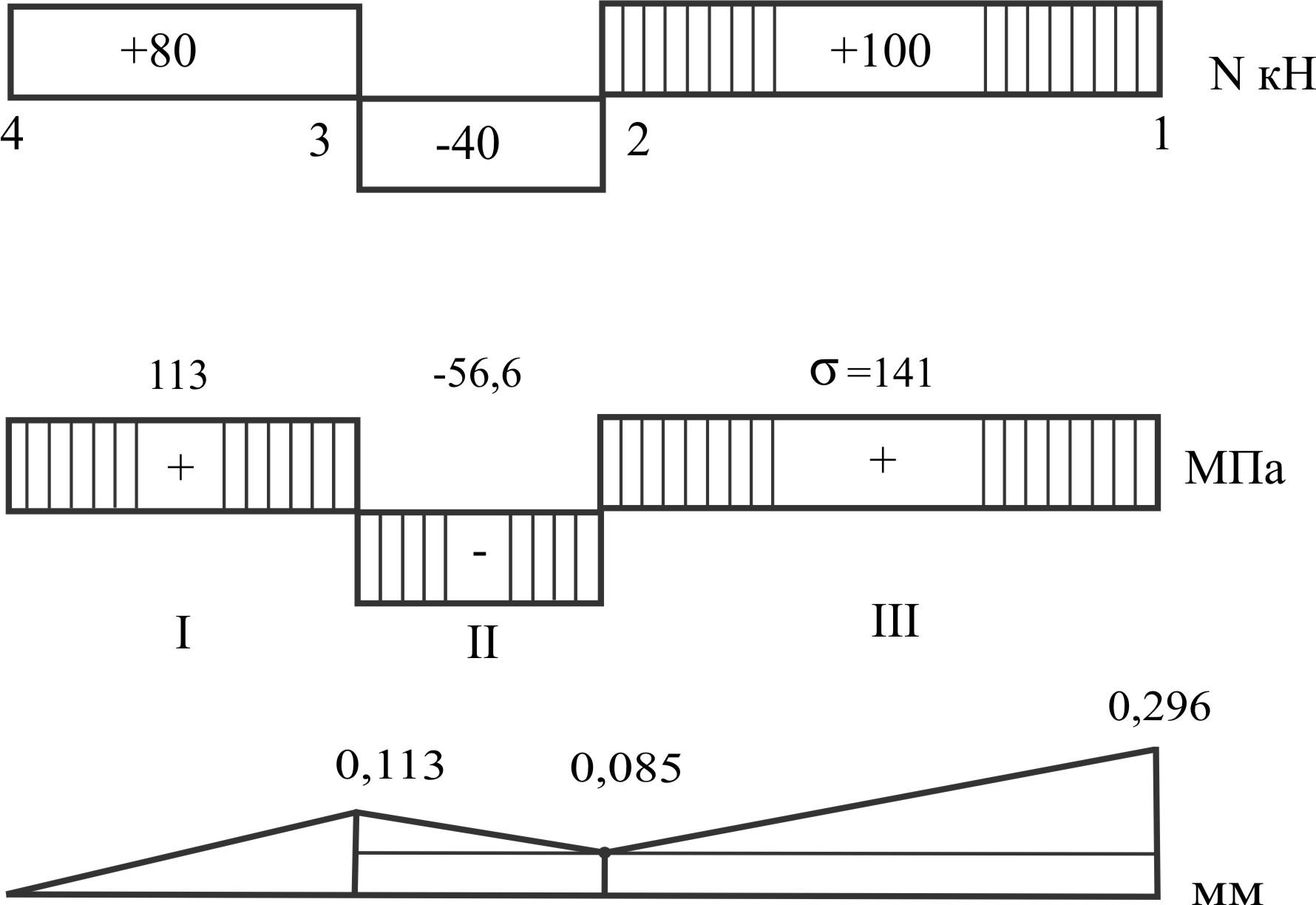
σ
=
![]() .
.
F
=
![]() D2.
D2.
∆ℓi
= ωi
=
![]() ℓi.
ℓi.
ω
= Σ
ωi.
∆ℓ1
= ω1
= 0,113,
∆ℓ2
= — 0,028, ω2
= 0,085,
∆ℓ3
= 0,211, ω3
= 0,296.
Пример 9.
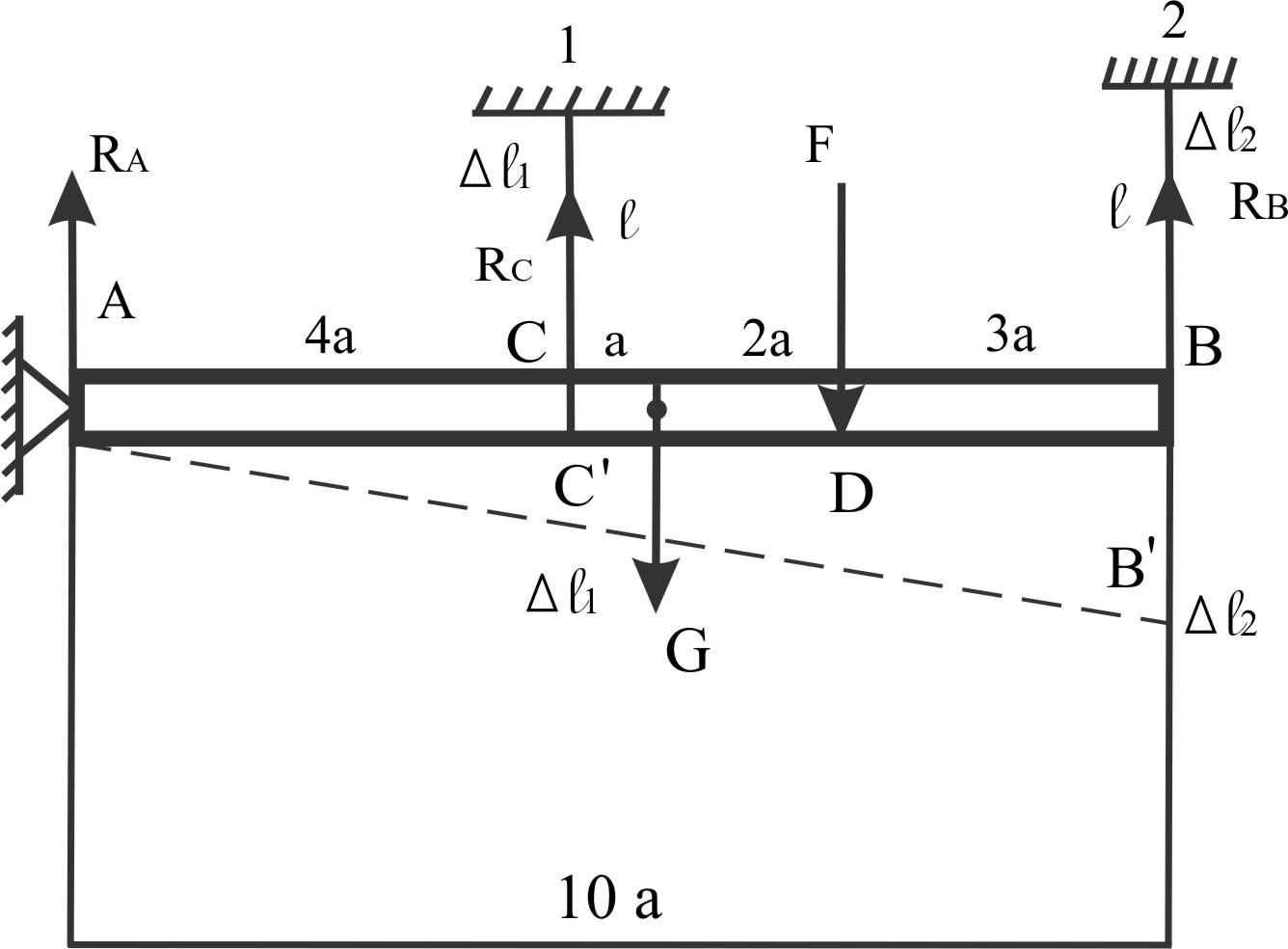
Абсолютно жесткая
балка
В «С» и «В»
подвес на стержнях
ℓ =
2 м; в «D»
— F
= 20 кН;
сечение
А1
= 3 см2;
А2
= 6 см2
E
= 2×105
МПа
Gбалки
= 40 кН
Определить
σ1
и σ2
(напряжения в стержнях подвеса).
Решение:
Введя
реакции RA;
RC
и RB
имеем 3 неизвестных, уравнений равновесия
2 (для сил и моментов), значит задача
статически неопределима, следовательно
необходимо использовать геометрическое
уравнение для перемещений
∆ ACC’
~ ∆ ABB’, ε1
= ε2.
![]()
,
∆ℓ2
= 2,5 ∆ℓ1.
∑MA
= 0; RC
4а
— G 5a — F 7a + RB·10a
= 0,
4
RC
+ 10 RB
= 5 G + 7 F
![]()
/
![]() ;
;
2,5
=
![]() ;
;
RB
= 5 RC;
54
RC
= 340;
RC
= 6,3 кН
RB
= 31,5 кН
σ1
=
![]()
= 21 МПа.
σ2
=
![]()
= 52 МПа.
Пример 10.
Ступенчатый брус
а = 0,2 м; в = 0,4 м; с =
0,8 м;
Fa
= 15 см2;
Fв
= 10 см2;
FC
= 5 см2
нагружен
силами Pa
= — 120 кН; Pв
= 60 кН; PС
= — 20 кН
E
= 2×105
МПа

Построить
эпюры N,
σ,
ε, ω сечений.
Решение:
Продольные силы
строим от свободного конца; на участках
алгебраически суммируем силы по одну
сторону сечения. Перемещение определяют
от защемленного.
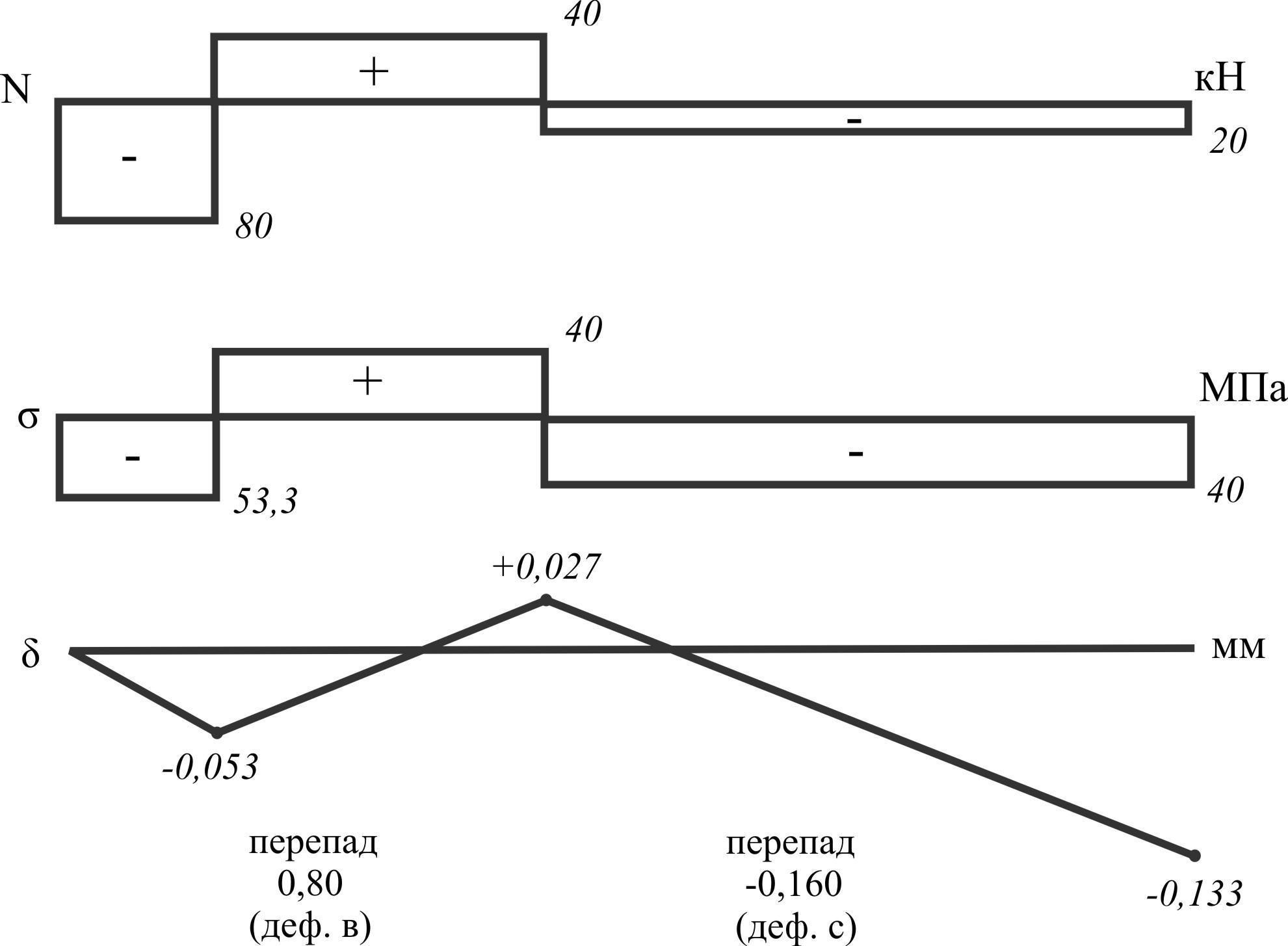
Перемещение сечений
= алгебраической сумме деформации
участков.
σ
=
![]() ,
,
ε
=
![]() ,
,
ω
= εℓ = ∑ εiℓi.
δ1
= ε1ℓ1
= ∆ℓ1.
δ2
= δ1
+ ∆ℓ2
= ε1ℓ1
+ ε2ℓ2
= 0,080 — 0,053 = 0,027.
δ3
= δ2
+ ε3ℓ3
= 0,027 —
160×10-3
= -0,133.
Пример
11.
Дан брус (размеры
и приложенные силы) — см. рис. ниже.
Построить
эпюры N,
σ,
ω.
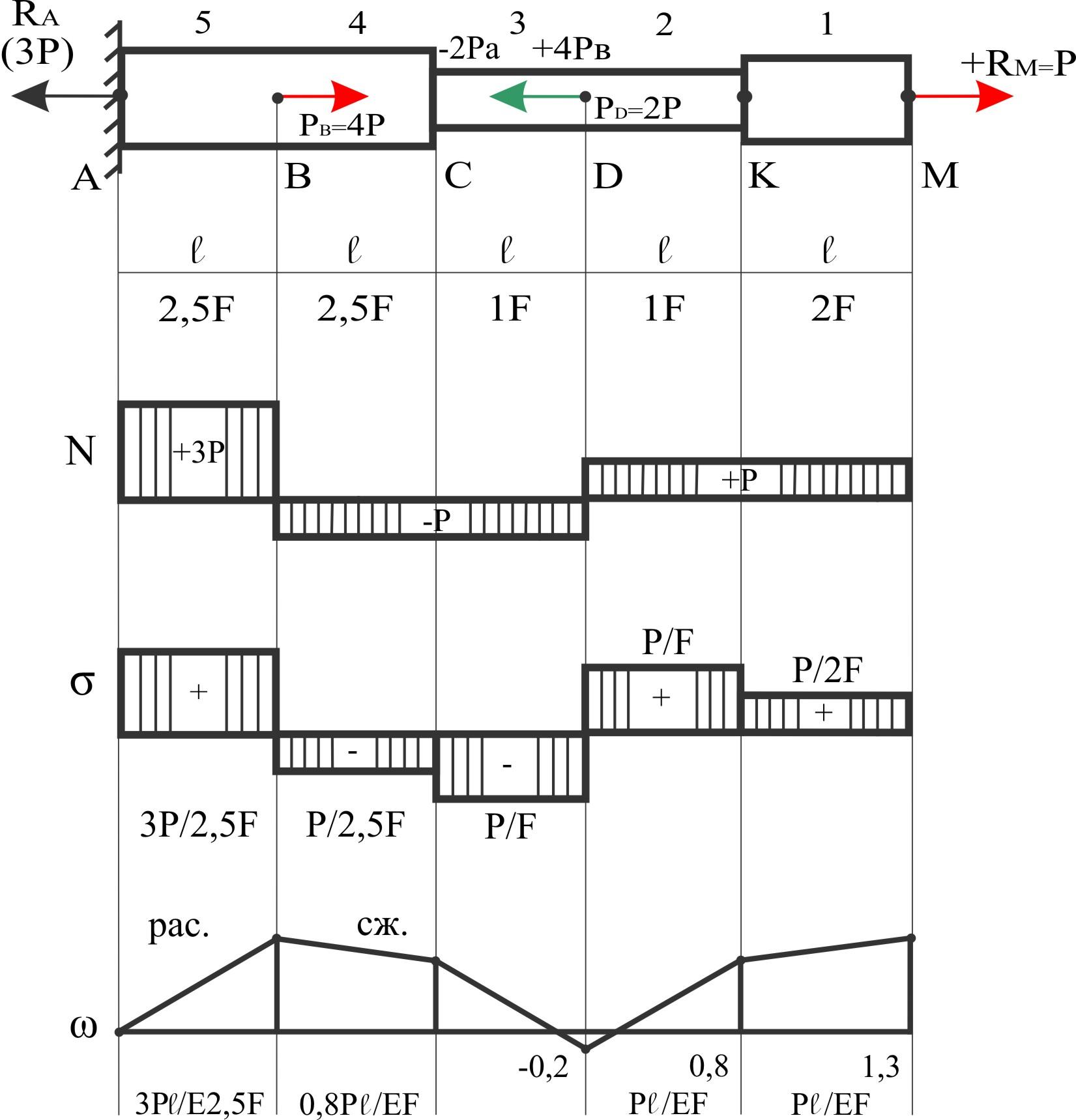
Решение:
Построение
N
и σ
от свободного конца, перемещений ω от
заделки
σ
=
![]() .
.
Скачки
в сечениях, где приложены силы (+ при
совпадении направления сил и оси Z).
(5)
ωB
= ∆ℓ1
=
![]()
=
![]() .
.
(4)
ωC
= ωB
+ ∆ℓ2
= 1,2
![]()
+
![]()
= (1,2 — 0,4)![]()
= 0,8
![]() .
.
(3)
ωD
= ωC
+ ∆ℓ3
= 0,8![]()
+
![]()
= (0,8 — c)![]()
= -0,2
![]() .
.
(2)
ωK
= ωD
+ ∆ℓ2
= -0,2![]()
+
![]()
= 0,8![]() .
.
(1)
ωM
= ωK
+ ∆ℓ1
= 0,8![]()
+
![]()
= 1,3![]() .
.
П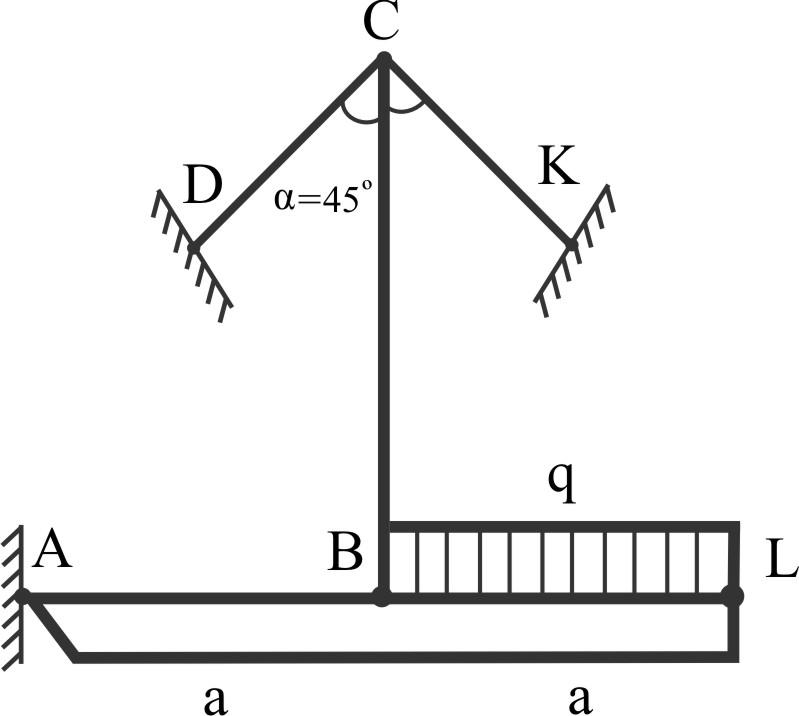 ример
ример
12.
a
= 1,2 м
q
= 50 кН/м
α = 45º
[σ]
= 150 МПа
Определить
диаметры BC,
CD
и CK,
обеспечивающие прочность конструкции.
Решение:
Изобразим силы в
стержнях. Применим метод сечений.

I
Уравнение равновесия AL:
∑MA
= 0
R1a
— qa·1,5a = 0; R1
= N1
= 1,5 qa;
→ →
R1
= — N1.
II
Уравнение равновесия узла C:
∑X
= 0; N2
sin 45 — N3
sin 45 = 0; N2
= N3.
∑Y
= 0; 2 N2
cos
45 — N1
= 0; N2
= N3
=
![]() .
.
На основании
требований прочности:
A1
= F1
=
![]()
=
![]()
=
![]()
=
![]()
= 0,6·10-3
м2,
d1
=
![]()
= 27,5 мм
≈ 28.
A2
= F2
= A3
= F3
=
![]()
=
![]()
= 0,424·10-3
м2,
d2
= d3
=
![]()
= 23,2 мм ≈ 23.
При
d2
= d3
= 23, σ2
= σ3
= 157 МПа > σ на 4,66%,
d2
= d3
= 24, σ2
= σ3
= 141 МПа < σ на 6%.
Окончательно
берем d2
= d3
= 24, т.к. по ГОСТ
![]()
≤ 3% (превышение расчета над допустимыми
≤ 3%).
Пример
13.
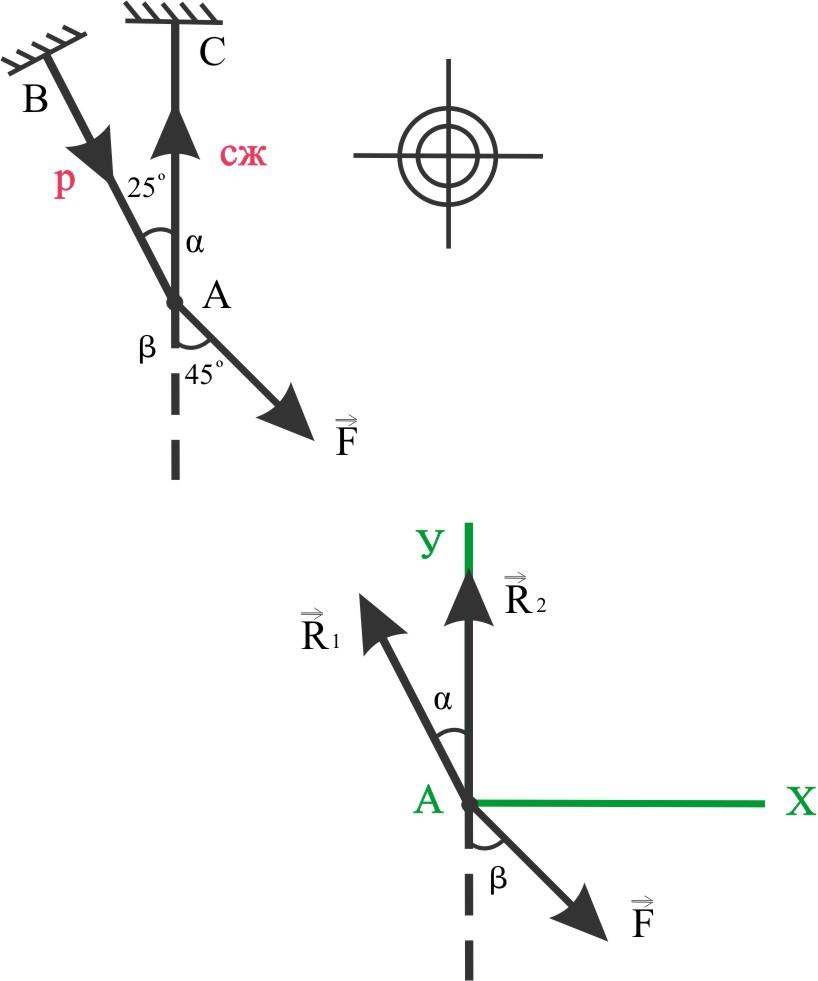
Труба дюралюминий
30×24
[σ] = 75 МПа
→
Определить
допускаемую F
— силу в точке A.
Решение:
Изобразим силы,
после чего:
I
Вырежем А.
II
Составим уравнение равновесия
∑X
= F sin β — R1
sin α = 0,
R1
= 1,67 F; R1
= N1.
∑Y
= R1
cos α + R2
— F cos β = 0,
R2
= F cos β — R1
cos α = -0,806 F.
N1
> N2,
N1
= 1,67 F = A [σ],
F
=
![]()
= 11,4 кН.
|σAC
| =
![]()
=
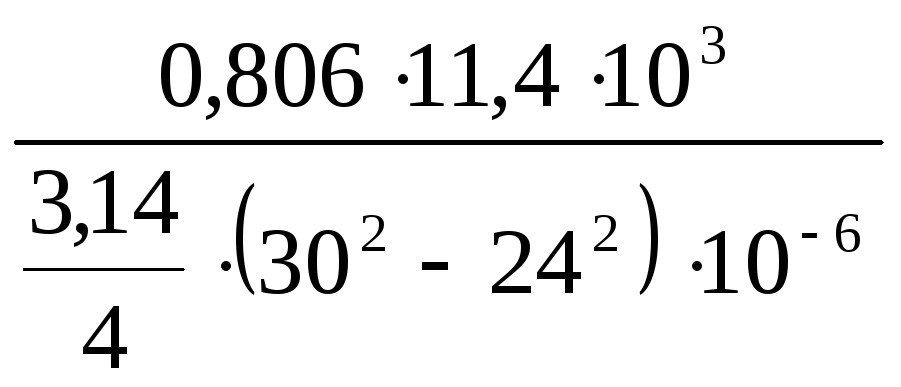
= 36,1 МПа
< [σ].
Нерациональность
конструкции σAC
< σAB
на 53%. AC
желательно меньшего сечения.
Пример
14.
Стержни из
одинакового материала
Балка жесткая и
невесомая
Сечения одинаковые
у стержней.
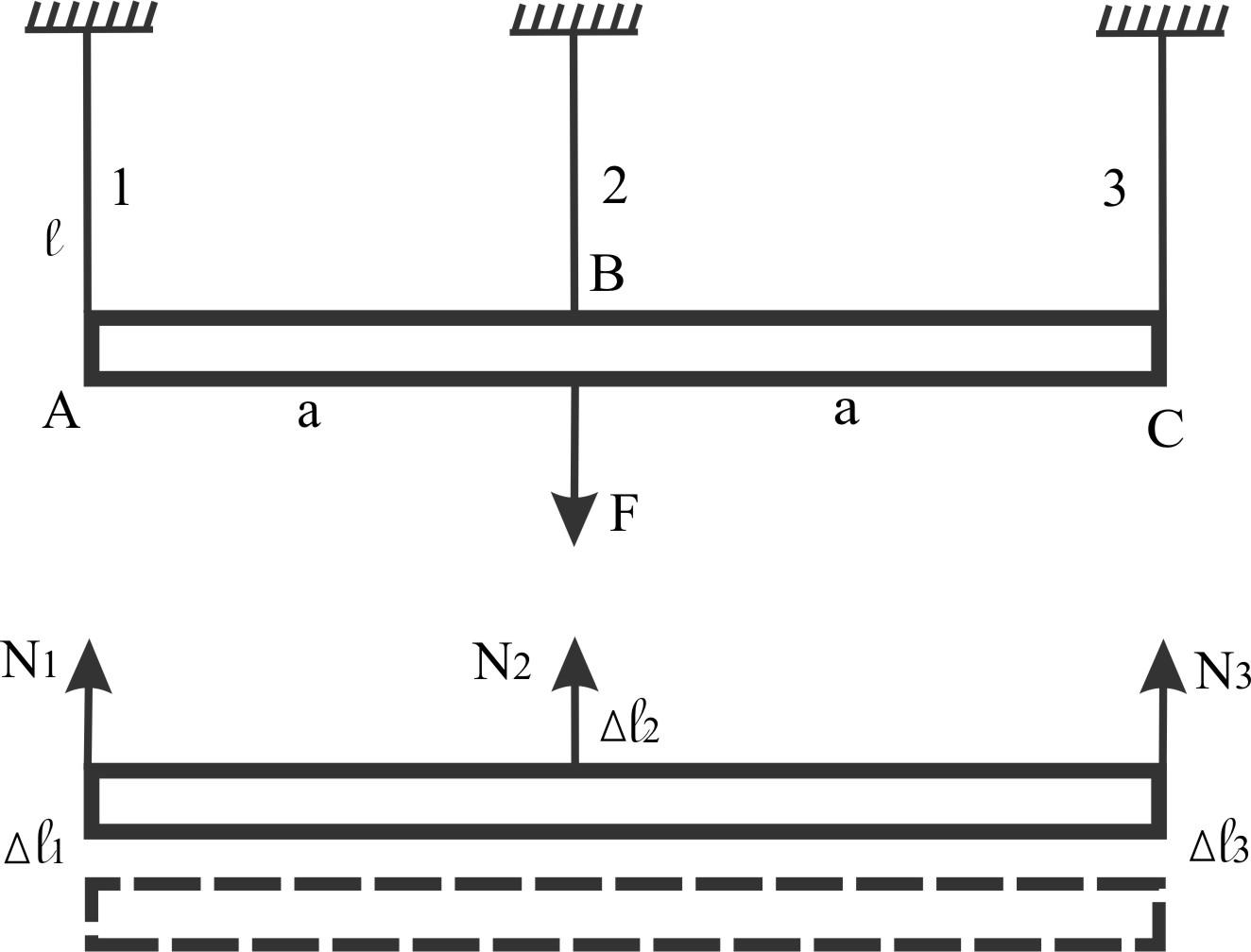
Определить силы
в стержнях, на которых подвешена балка.
Решение:
Неизвестных
сил 3: N1,
N2,
N3.
Уравнений
равновесия 2: ∑Y
= 0; ∑МВ
= 0.
Система статически
неопределима
1
раз «3 — 2»
.
Симметрия
системы ∆ℓ1
= ∆ℓ2
= ∆ℓ3
N1a
— N3a
= 0; N1
= N3.
Требуется учесть
геометрическую сторону
![]()
=
![]()
=
![]() ;
;
N1
= N2
= N3
=
![]()
— полученный результат
симметрия
+ одинаковость жесткостей EA
= const.
Может оказаться:
Неодинаковость
сечений.Неодинаковость
длин.Неодинаковость
материала.Комбинации
различий.
(достигается разное
распределение нагрузок).
Пример.
A1
= A3
= 2А; A2
= А; ∆ℓ1
= ∆ℓ2
= ∆ℓ3,
![]()
=
N2
=
![]()
подставим в уравнение равновесия
N1
= N3
= 0,4 F;
N2
= 0,2 F.
В более жестких
системах большие силы.
Пример
15.
Дана конструкция:
защемлен с 2 концов
А
= 3 см2
F
= 60 кН
Cm
4 (σТ
= 260 МПа)
[пТ]
= 1,6

Построить
эпюры: N,
σ, перемещение α поперечных сечений.
Решение:
В
заделках A
и B
возникают реакции.
Уравнение
равновесия ∑ Z
= 0; — RA
+ F1
+ F2
— RB
= 0.
Неизвестных 2, а
уравнение 1, следовательно система 1 раз
статически неопределенная.
II
геометрическое уравнение — уравнение
перемещений, но для его составления
заменим одну заделку ее реакцией RB
= Х (B
— свободно), следовательно статически
определенный брус с 1 неизвестным RA,
у которого λВ
= 0 = λВF1
+ λВF2
+ λВX.
По закону Гука
перемещение сечений определяется суммой
деформаций участков между приложенными
силами:
λВF1
= ∆AC
=
![]()
— удлинение.
λВF2
= ∆AD
+ ∆ED
=
![]()
+
![]()
— удлинение.
λВX
= —![]()
— укорочение.
Из
λВ
следует
![]() ,
,
X
=
![]()
— теперь задача статически определимая,
брус нагружен силами
![]() .
.
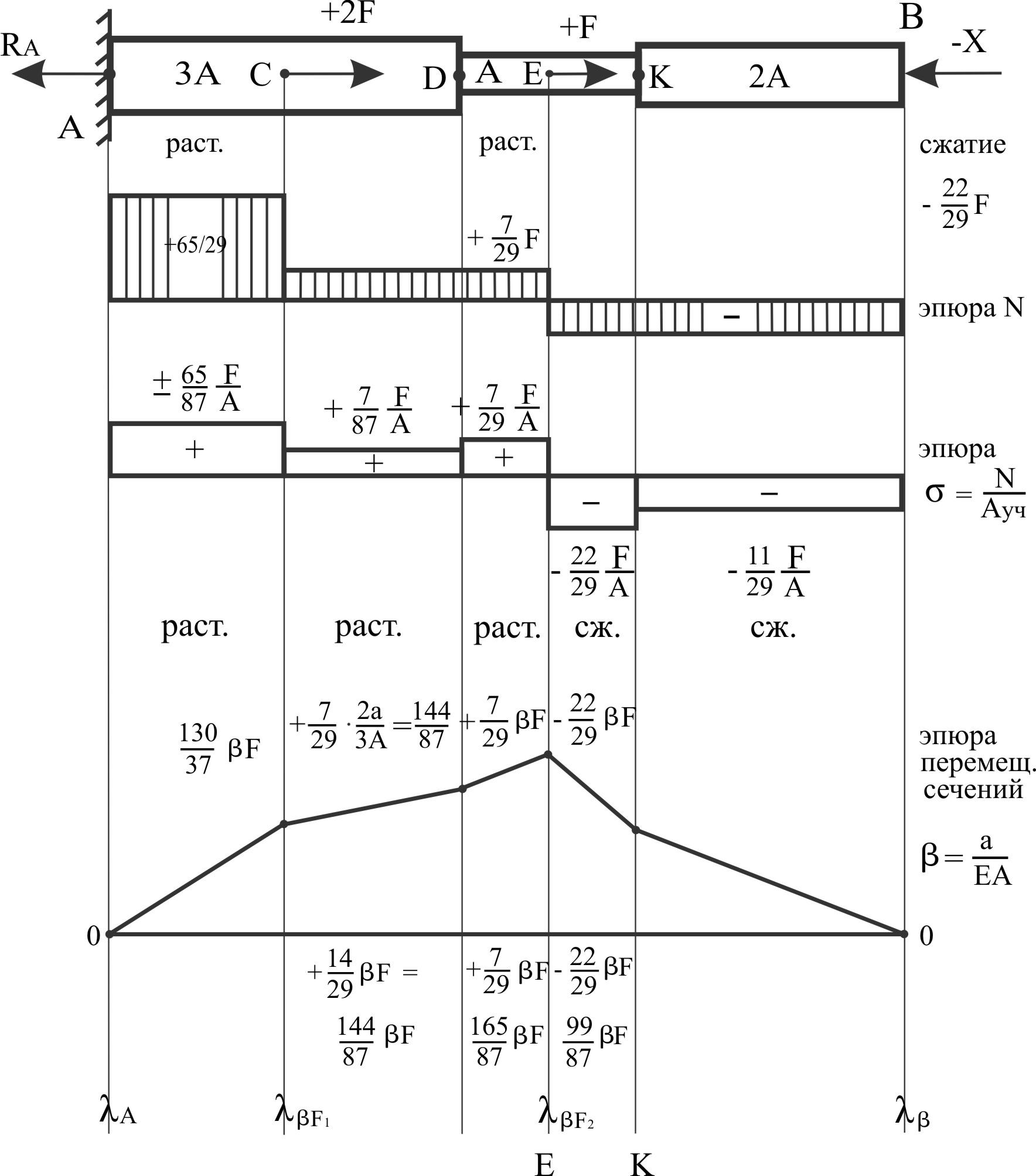
σ
наибольшая в E
· K
— опасная зона EK
проверка прочности
пт
=
![]()
=
![]()
=
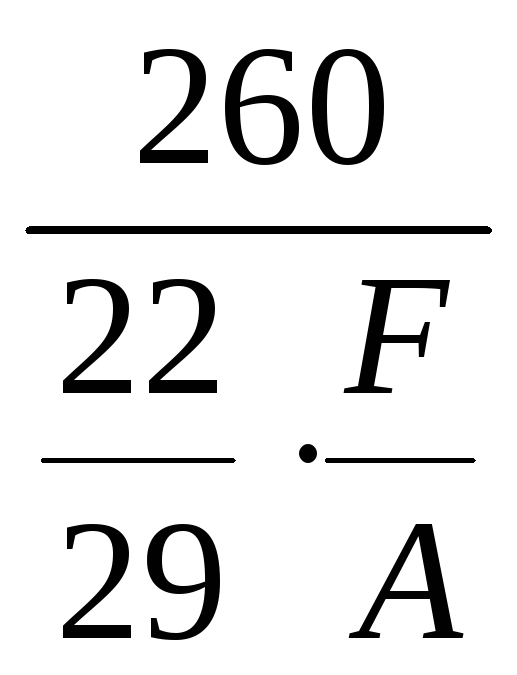
=
![]()
= 1,72.
пт
> [п] обеспечена.
Пример
16.
Дана балка
переменного сечения, защемленная в
точке А, второй конец В свободен. Имеется
зазор δ на свободном конце.
Из примера № 15
создадим справа зазор.
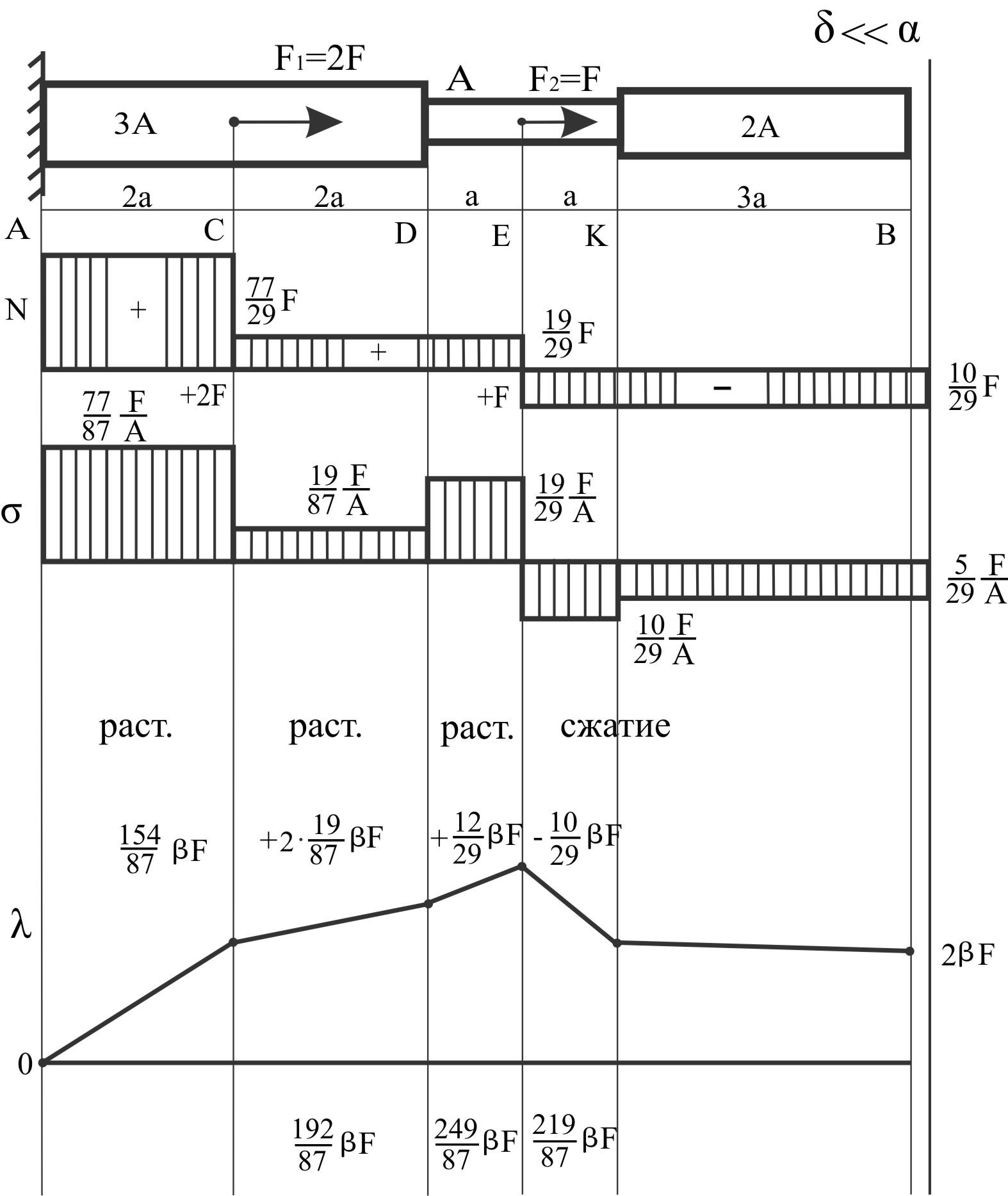
А
= 3 см2
F
= 60 кН
β
=
![]()
σ
=
![]()
соответствует
начальному
зазору
Суммарное
перемещение правого торца λВ
= δ.
Для
определенности предположим δ =
![]()
= 2 βF.
При
свободном B
(без защемления): λВ
= λВF1
+ λВF2
=![]() +
+![]() +
+![]() =
=![]() βF
βF
> δ, т.е. возникает в B
реакциях и задача статически неопределима,
следовательно кроме уравнения равновесия
нужно уравнение перемещений.
Для
случая X
=
![]()
F
λВ
= λВF1
+ λВF2
+ λВX
= δ,
λВF1
+ λВF2
=
![]()
βF
+
![]()
=
![]()
βF
—
![]()
βX.
Эпюры
сил N
строим от «свободного» конца B,
эпюры напряжений по эпюрам N,
следовательно σ =
![]() .
.
Эпюру λ, используя
закон Гука, для деформаций участков.
Пример 17.
Определить
диаметр поперечного сечения стержня,
в котором τmax
≤ 80 МПа. Продольная сила N
= F
= 90 кН.
Решение:
τ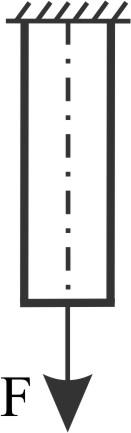 αmax
αmax
=
![]()
при α = 45°, откуда σz
= 2 ταmax = 2·80 МПа.
Но
σz=
![]() ,
,
т.е. А ≥
![]() .
.
Для
круга А =
![]()
≥
![]() .
.
Что
позволяет найти d≥![]() =
=![]() =26,8·10-3м=
=26,8·10-3м=
26,8мм.
Пример 18.
В
наклонном сечении сжатого стержня σα
= -60 МПа, τα
= 24 МПа.
Определить
σmax
и τmax.
Решение.
Д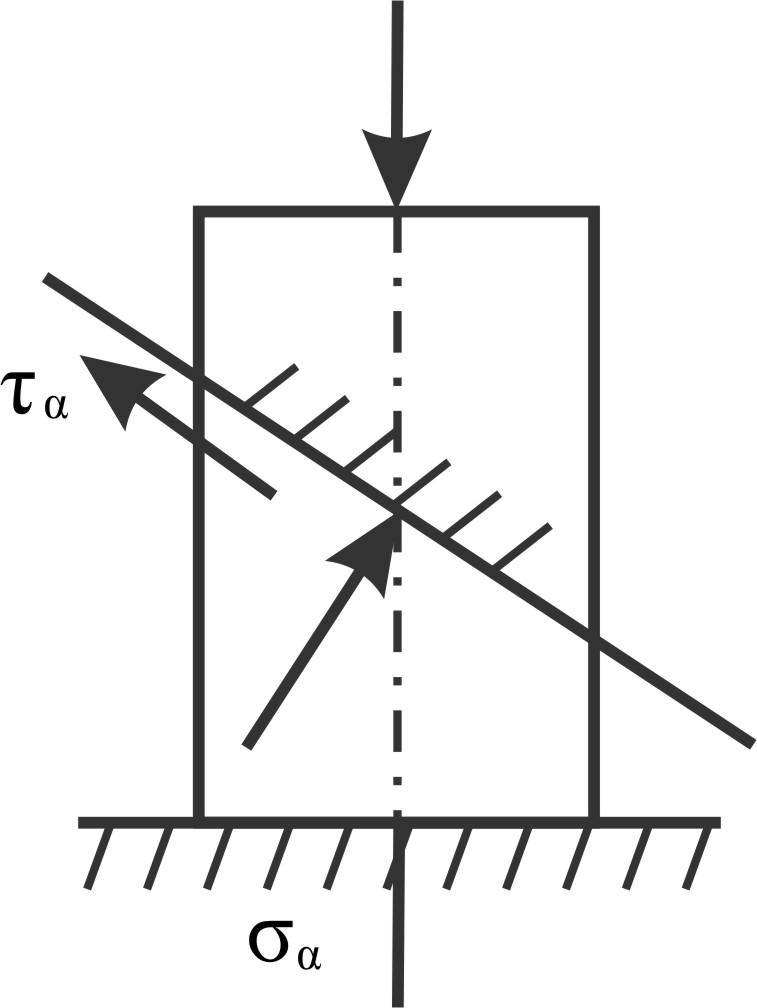 ля
ля
наклонного сечения σα
= σz
cos2α
и τα
=![]()
sin
2 α.
Из этих формул
определим положение сечения
![]()
=
![]()
= tg
α,
т.е. tg
α
=
![]()
= -0,4.
Но
cos2α
=
![]()
=
![]()
= 0,862,
после
чего σz
=
![]()
= —
![]()
= — 69,6 МПа.
|
τmax
| =
![]()
=
![]()
МПа = 34,8 МПа.
Пример 19.
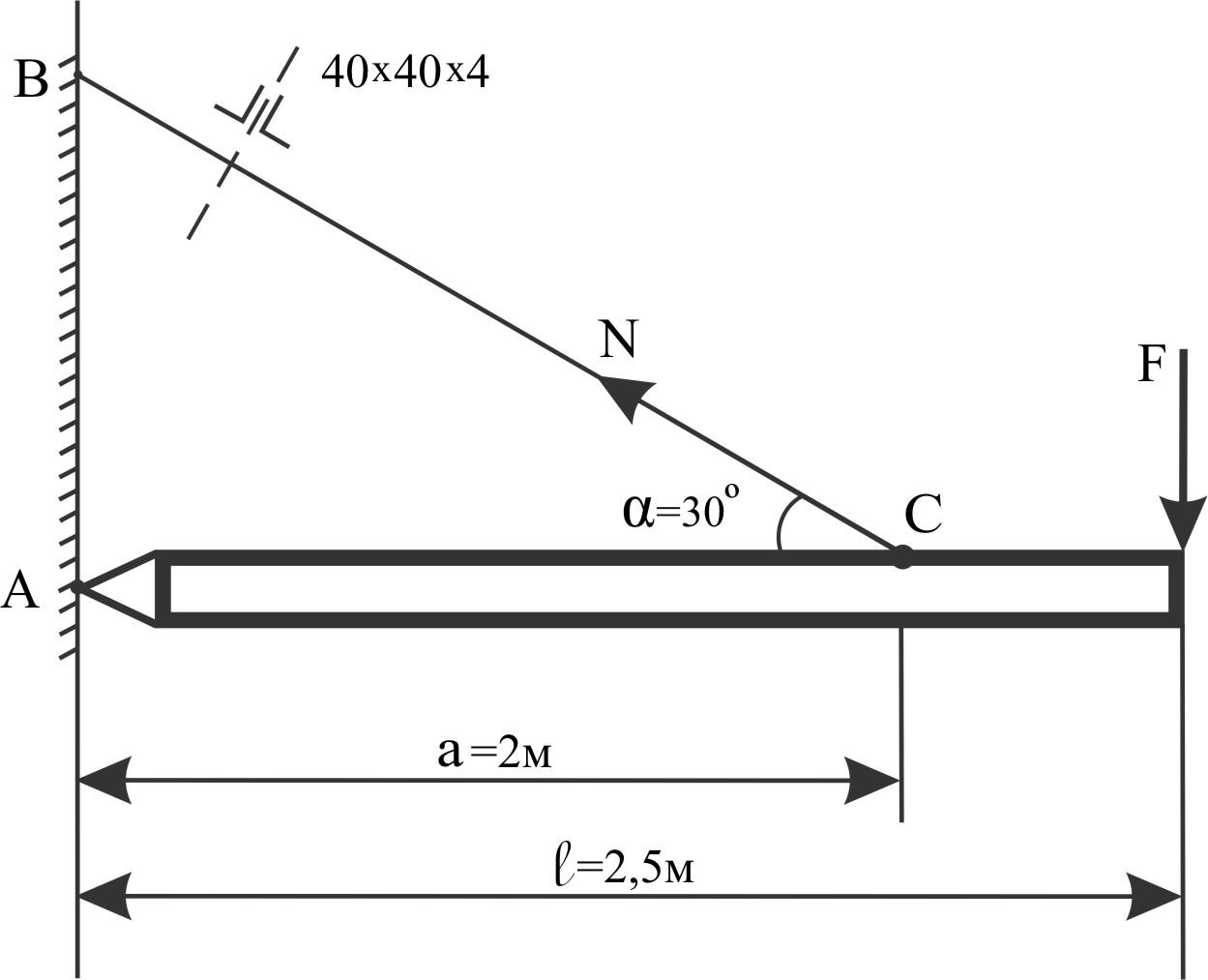
Конструкция
изображена на рисунке:
тяга
BC
сварена из 2 уголков из ст 3, для которой
[σ] = 160 МПа, F
= 40 кН.
Проверить расчетом
прочность тяги.
 Решение:
Решение:
Продольную
силу N
определим из условия равновесия:
∑M
= 0; Fℓ
— N
sin
α
= 0, откуда
N
=
![]()
=
![]()
= 100 кН.
После
чего σ =
![]() ,
,
A
= 2A1
(сварено 2).
A1
берем из справочника (для уголка 40×40×4
по ГОСТ 8509-86 A1
= 3,08 см2).
Считаем
σ =
![]()
Па = 162·106
Па.
Допускается
кратковременная перегрузка до 5%.
У
нас
![]()
= 1,25%, т.е. прочность удовлетворительна.
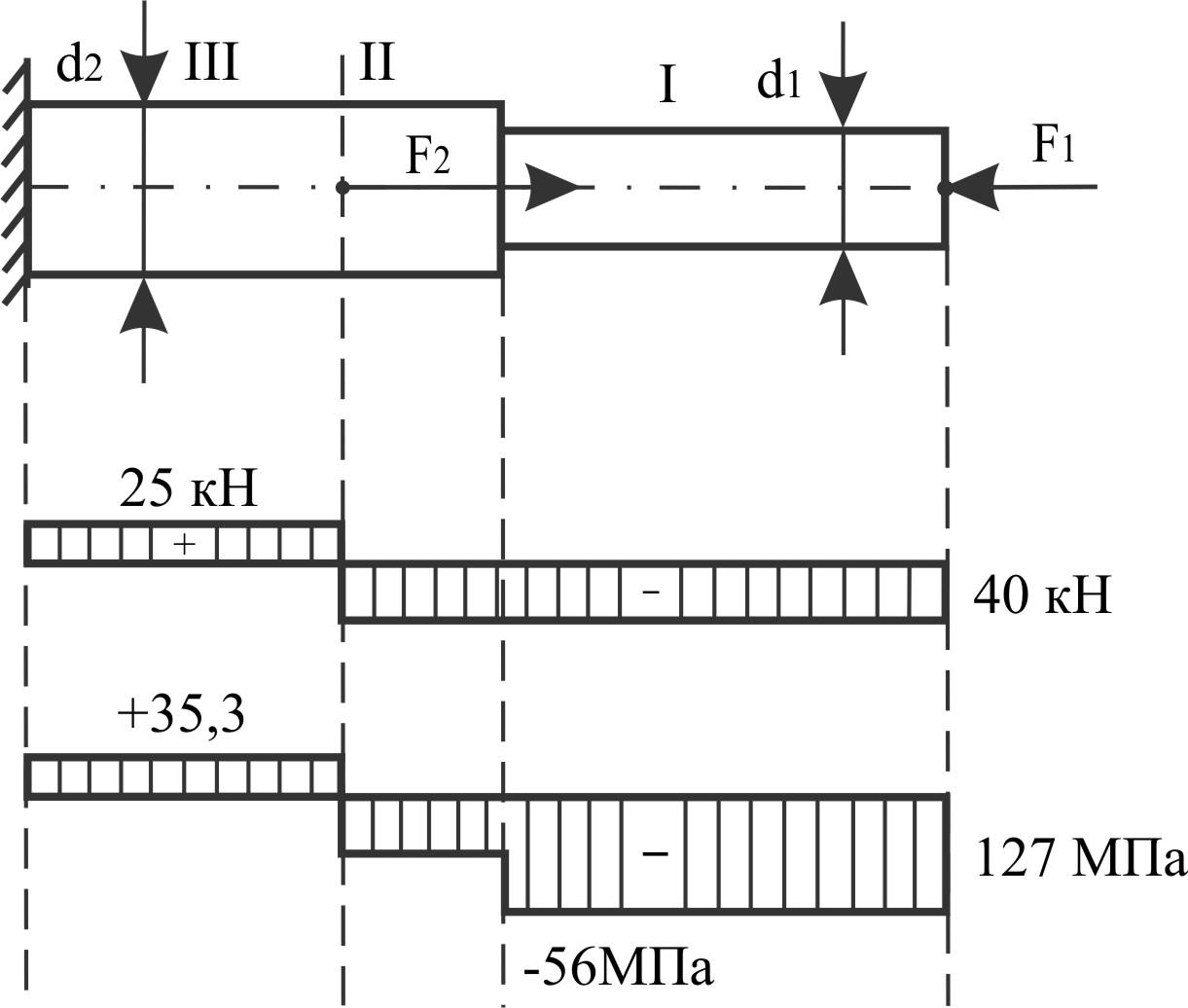
Пример 20.
Ступенчатый
чугунный брус d1
= 20 мм; d2
= 30 мм должен иметь коэффициент запаса
прочности [п] = 4. Материал имеет σпч.раст.
= 150 МПа, σпч.сжат.
= 580 МПа. Приложенные нагрузки F1
= 40 кН, F2
= 65 кН.
Проверить на
прочность.
Решение:
Строим
эпюры N
и σ =
![]() .
.
Наибольшее
напряжение на I
(сжатие). Для него п =
![]() =
=![]() =4,57.
=4,57.
Участок
III
— растяжение п =
![]()
=
![]()
= 4,25.
Оба
пI
и пIII
больше требуемого, т.е. прочность
обеспечена.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
19.11.2019175.62 Кб0Рабочая_Программа_ИСЭ_Кир01.doc
- #
- #
- #
- #
Источник
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
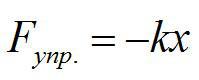
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
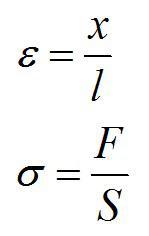
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
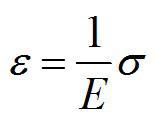
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
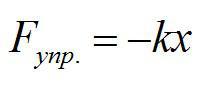
По третьему закону Ньютона:
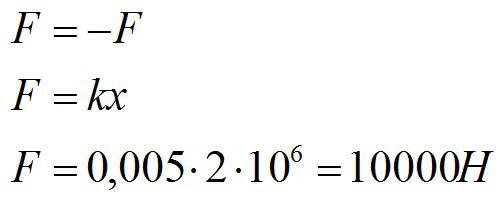
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
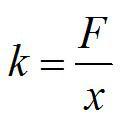
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
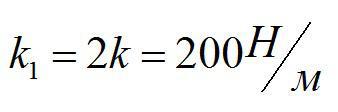
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
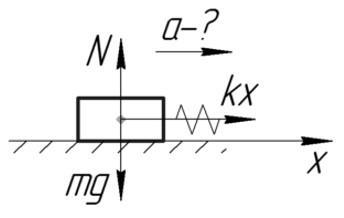
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
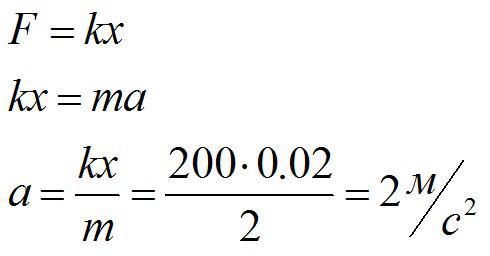
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
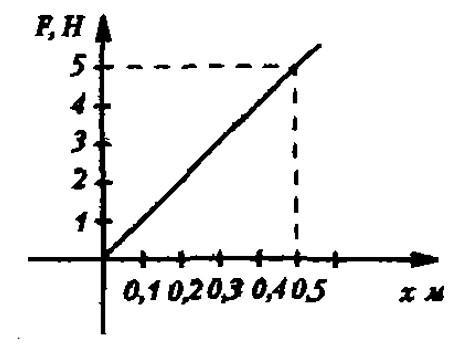
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Ус
