Условие прочности при косом изгибе с растяжением
Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения.
Косой изгиб.
Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса.
В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.
Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Условие прочности при косом изгибе:
где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси.
Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности:
где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей.
Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям.
Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей:
Изгиб с растяжением (сжатием).
При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M.
Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса:
К расчёту на прочность бруса при изгибе с растяжением:
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид:
Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле:
где А — площадь поперечного сечения.
Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле:
Условие прочночти имеет вид:
Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям.
Внецентренное растяжение или сжатие.
При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.
К расчёту на прочность бруса при внецентренном растяжении
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Приведём силу F к центру тяжести:
где уF , xF — координаты точки приложения силы F.
В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле:
Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:
Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.
Кручение с изгибом.
Сочетание деформаций изгиба и кручения характерно для работы валов машин.
Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения:
Эпюры напряжений в сечении бруса при кручении с изгибом
Нормальное напряжение достигает максимума на поверхности:
Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала:
Из третьей и четвёртой теории прочности:
При кручении с изгибом условие прочности имеет вид:
Источник
Косым изгибом называется разновидность сложного сопротивления, при которой плоскость действия результирующего изгибающего момента не совпадает ни с одной из плоскостей симметрии поперечного сечения.
Вся нагрузка расположена частично в одной плоскости, частично в другой.
| При косом изгибе действующие внешние силы (моменты) представляют их проекциями на главные оси поперечного сечения (рис. 7.1, б), тем самым сводят задачу к случаю поперечного изгиба в двух главных плоскостях. Из рис. 7.1, а, б видно, что: |
| Изгибающие моменты в расчетном сечении: |
| При выбранном направлении главных центральных осей инерции положительным октантом будет первый октант (на рис. 7.1, а, б заштрихован). |
| Нулевая линия – это геометрическое место точек поперечного сечения стержня, в которыхнормальные напряжения равны нулю. Из определения нейтральной линии легко находится положение нейтральной линии, приравнивая правую часть выражения к нулю: , . Обозначив через угол наклона нулевой линии к оси x и , придем к уравнению нулевой линии: . Из анализа уравнения, нулевая линия при косом изгибе не проходит перпендикулярно к силовой линии (рис. 9.2). Угол между нейтральной и силовой линиями будет прямым, только если главные центральные моменты инерции равны ( ), но это не прямой изгиб! Косой изгиб невозможен для балок с сечениями, у которых все центральные оси являются главными (например, квадрат, круг). |
| Правило знаков. Изгибающие моменты в расчетном поперечном сечении считаются положительными, если они вызывают в первом (заштрихованном) октанте напряжения растяжения. |
| Нормальные напряжения в точках поперечного сечения с текущими координатами х, у определяются алгебраической суммой напряжений, вызываемых изгибающими моментами Мx и Мy: |
| где Jx и Jy — моменты инерции поперечного сечения относительно главных, центральных осей инерции сечения X, Y, т. е. изменяются по линейному закону. Уравнение нейтральной (нулевой) линии в сечении найдем, приравняв |
| Ответы совпали. |
| При х = 0 значение у = 0, т. е. прямая с угловым коэффициентом k проходит через центр тяжести поперечного сечения. |
| При косом изгибе нейтральная линия представляет собой прямую, которая не перпендикулярна к плоскости изгибающего момента , или, что одно и то же, к силовой линии. |
| Силовая линия наклонена к оси X под углом а, следовательно, ее угловой коэффициент равен: |
| Угловой коэффициент нейтральной линии: |
| Так как в общем случае Jx не равно Jy, то и k1 не равно — 1/k, следовательно, нулевая длина не перпендикулярна силовой линии, а повернута в сторону главной оси минимального момента инерции. |
| Нейтральная линия разделяет поперечное сечение на две зоны: |
| в которой действуют только напряжения растяжения; в которой действуют только напряжения сжатия. Первый (заштрихованный) квадрант (рис 7.1, а) находится всегда в зоне действия напряжений растяжения. Максимальные по величине нормальные напряжения находятся в точках поперечного сечения максимально удаленных от нейтральной оси. |
| Максимальные по величине напряжения растяжения возникают в точке А с координатами Xa, Yл, а максимальные напряжения сжатия возникают в точке В с координатами XВ, YВ (рис. 7.1, в): |
| Получим эпюру нормальных напряжений в расчетном сечении (7.1, в). |
| Условие прочности. Если материал стержня одинаково работает на растяжение и на сжатие, то условие прочности записывается в виде: |
| Если материал стержня работает на растяжение и на сжатие не одинаково, то расчет проводится раздельно, т. е. проверяются условия прочности: |
| Для поперечных сечений, имеющих две оси симметрии: |
| где Wx, Wy — момент сопротивления поперечного сечения относительно главных, центральных осей инерции X, Y. |
| Прогибы при косом изгибе. Прогиб конца консоли от действия Рx направлен по оси X и равен: |
| Прогиб от действия Рy направлен по оси Y и равен: |
| Модуль полного прогиба конца консоли |
| Угол наклона вектора f к оси X |
| т. е. угловой коэффициент |
| перемножив k на k2 получим: |
| что свидетельствует о том, что нулевая линия и направление полного прогиба взаимно |
Условия прочности
— для сечения произвольной формы
— для сечений типа прямоугольник, двутавр, швеллер
Источник
Лекция 14. СЛОЖНОЕ СОПРОТИВЛЕНИЕ
Понятие о сложном сопротивлении, его виды. Изгиб с растяжением. Косой изгиб.
Cложное сопротивление – такие виды нагружения бруса, при которых
в поперечных сечениях возникают одновременно не менее двух внутренних
силовых факторов.
Случаи сложного сопротивления условно разделяют на два вида.
Первый вид составляют случаи сложного сопротивления, при которых
в опасных точках бруса напряженное состояние является одноосным. В эту
группу объединяют: изгиб с растяжением, косой изгиб, внецентренное
растяжение-сжатие и др.
Рис. 41. Изгиб с растяжением
Условие прочности при изгибе с растяжением, пренебрегая действием поперечных сил, имеет вид:
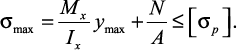(32)
Ко второй группе относятся такие случаи сложного сопротивления,
когда напряженное состояние является плоским. Например, изгиб
с кручением, растяжение(сжатие) с кручением и т.д. Для случая
нагружения, относящегося к первой группе, в отличие от второй группы,
нет необходимости в применении гипотез прочности.
Косой изгиб проявляется, если прикладываем к балке вертикальную
нагрузку, и она при этом изгибается не только в вертикальной плоскости,
но и вбок. Косой изгиб – это изгиб, при котором изогнутая ось стержня не
лежит в силовой плоскости. Косой изгиб невозможен для балок
с сечениями, у которых все центральные оси являются главными (например,
квадрат, круг).
Рассмотрим консольную балку прямоугольного сечения длиной l,
нагруженную вертикальной силой P. Главная центральная ось балки (ось
симметрии) y составляет некоторый малый угол α с направлением действия
нагрузки.
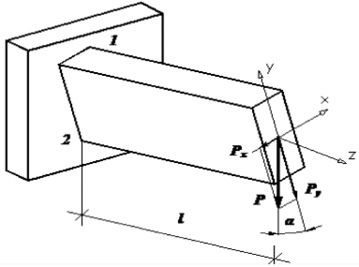
Рис. 42. Косой изгиб
Разложим силу P на составляющие: Py = cos α, Px = sin α .
Используя принцип независимости действия сил Py, рассмотрим отдельно
действие каждой составляющей. Нагрузки Py и Px вызывают в поперечном
сечении, расположенном на некотором расстоянии z от правого конца балки,
изгибающие моменты:
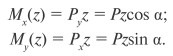
Оба изгибающих момента будут наибольшими в жесткой заделке:
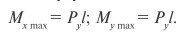
Формула суммарных нормальных напряжений при косом изгибе
в произвольном поперечном сечении балки для некоторой точки
с координатами x и y:
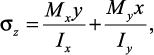(33)
где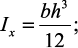 
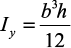
– главные моменты инерции; h – высота, а b – ширина прямоугольного
поперечного сечения балки. Величины изгибающих моментов и координат
данной точки подставляются в формулу нормальных напряжений при косом
изгибе, знак каждого из слагаемых определяется по физическому смыслу.
Наибольшие нормальные напряжения при косом изгибе возникнут
в поперечном сечении, расположенном в жесткой заделке, в наиболее
удаленных от соответствующих нейтральных осей точках 1 и 2: y = h/2,
x = b/2. В точке 1 напряжения будут растягивающими:
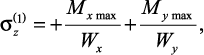
а в точке 2 – такими же по величине, но сжимающими.
В формулах максимальных нормальных напряжений при косом изгибе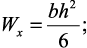 
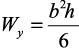– осевые моменты сопротивления балки относительно главных центральных осей инерции.
Нейтральная линия – это геометрическое место точек поперечного сечения стержня, в которых нормальные напряжения равны нулю.
Из определения нейтральной линии легко находится положение нейтральной линии, приравнивая правую часть выражения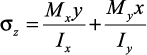 
к нулю:
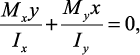
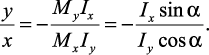
При косом изгибе условие прочности имеет вид:
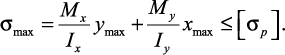(34)
Косой изгиб опасен тем, что при производственном браке (перекосе) могут существенно увеличиться нормальные напряжения в балке.
Источник
Косым изгибом называется такой изгиб, при котором плоскость действия суммарного изгибающего момента в сечении балки не совпадает с главными плоскостями инерции Оху или Oxz. Различают два вида косого изгиба: плоский и пространственный. При плоском косом изгибе (рис. 12.4, а) нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции. Эта плоскость называется силовой плоскостью, а линия ее пересечения с плоскостью поперечного сечения балки — силовой линией. При пространственном косом изгибе (рис. 12.4, б) нагрузки действуют в различных плоскостях.
Рис. 12.4
Обозначим через а^угол между силовой линией и главной осью Оу. Будем считать этот угол положительным при повороте силовой линии от оси Оу против хода часовой стрелки. Как при плоском, так и при пространственном косом изгибе суммарный изгибающий момент М, действующий в сечении балки (рис. 12.5, в), можно разложить на два изгибающих момента М и М,, действующих в главных плоскостях инерции:
Поделив первое из этих равенств на второе, выразим угол ар через отношение изгибающих моментов:
Из этого равенства видно, что если изгибающие моменты М и М имеют одинаковые знаки, то угол ар положителен. В этом случае силовая линия проходит через первую и третью четверти плоскости Oyz (рис. 12.5, б).
При плоском косом изгибе внутренние усилия М , Mz, Q , ()_ не являются независимыми, поскольку они определяются одними и теми же нагрузками, действующими в силовой плоскости. При этом угол (ХрОдин и тот же во всех сечениях. При пространственном изгибе внутренние усилия имеют различные законы изменения по длине балки, так как вычисляются от нагрузок, действующих в разных плоскостях. При этом величина угла ар также изменяется по длине балки.
Если в (12.1) положить N = 0, то получим формулу для нормальных напряжений при косом изгибе:
Здесь J и У. — главные моменты инерции сечения; у и z — координаты точек сечения.
Рис. 12.5
Из (12.4) видно, что при косом изгибе напряжения а изменяются по координатам у и z по линейному закону.
Положив в (12.4) о = 0, получим уравнение нулевой линии:
гдеу0 и — координаты точек нулевой линии (рис. 12.5, б). Выражение (12.5) является уравнением прямой, проходящей через начало координат.
Если обозначить через ос0 угол между нулевой линией и главной осью Oz, то из уравнения (12.5) найдем
Учитывая (12.3), получим соотношение, связывающее между собой углы а0 и а^,:
Знак минус в этой формуле указывает на то, что нулевая линия по отношению к силовой линии проходит через две другие четверти осей координат. Отсюда следует, что угол а0 откладывается от оси Oz в ту же сторону, что и угол ар от оси Оу (рис. 12.5, б).
На основании гипотезы плоских сечений при деформациях балки ее поперечные сечения поворачиваются вокруг нулевых линий. При этом наибольшие деформации удлинения и укорочения, а следовательно, и напряжения возникают в точках сечения, наиболее удаленных от нулевой линии. Таким образом, для вычисления наибольших напряжений в сечении необходимо подставить в формулу (12.4) координаты точек, наиболее удаленных от нулевой линии. Для сечений типа прямоугольника и двутавра, имеющих две оси симметрии, наибольшие по абсолютной величине напряжения удобно вычислять по формуле
где W , Wz — моменты сопротивления сечения.
На рис. 12.5, 6 показан характер эпюры нормальных напряжений для прямоугольного сечения. В этом случае наибольшие рас- тягивающие а» и сжимающие ст напряжения возникают в противоположных угловых точках сечения.
Условие прочности при косом изгибе для балок с отмеченным выше типом поперечного сечения имеет вид
а в случае произвольного сечения
В этих формулах М , Л/ — изгибающие моменты в опасном сечении балки; у, z— координаты точки, наиболее удаленной от нулевой линии. При использовании условия (12.9) величины М, Mz, у, z необходимо брать с учетом их знаков.
Важно заметить, что при пространственном изгибе положение опасного сечения не всегда является очевидным, так как изгибающие моменты М и Л/, возникают от действия различных нагрузок и не зависят друг от друга. В этих случаях необходимо проверять прочность в нескольких сечениях балки, например в сечениях, где М и М имеют наибольшие значения.
У z
Для определения прогибов балки при косом изгибе необходимо действующие на балку нагрузки разложить на составляющие, параллельные главным осям Оу, Oz, и определить по отдельности прогибы v и w по направлениям этих осей (рис. 12.6). Полный прогиб/в произвольном сечении балки и его направление определяются по формулам
Рис. 12.6
где оу— угол между направлением суммарного прогиба и осью Оу.
Аналогично могут быть найдены углы поворота сечений балки.
Рассмотрим примеры расчета балок при плоском и пространственном косом изгибе.
Пример 12.1. Деревянная консольная балка прямоугольного сечения (рис. 12.7) нагружена на свободном конце силой Р, направленной под углом ар = 30° к оси Оу. Нормативное значение нагрузки Рн = 3 кН, коэффициент надежности по нагрузке у^= 1,2. Расчетное сопротивление дерева (сосна) R = 13 МПа, модуль упругости Е = 104 МПа, коэффициент условий работы ус = 1. Размеры балки приведены на рис. 12.7, а, б.
Рис. 12.7
Построим эпюру нормальных напряжений для сечения в заделке, проверим прочность балки и определим прогиб на свободном конце.
Согласно СНиП при расчете на прочность необходимо брать расчетные нагрузки, а при определении перемещений — их нормативные значения.
Определим величину расчетной нагрузки и изгибающие моменты в заделке:
Главные моменты инерции и моменты сопротивления сечения равны
По формуле (12.6) находим положение нулевой линии:
По формуле (12.8) проверяем прочность балки:
Условие прочности выполняется. Эпюра нормальных напряжений для сечения балки в заделке приведена на рис. 12.7, б.
Для определения прогиба свободного конца балки разложим заданную нормативную нагрузку Рн на составляющие Р = Рнcos ар и Pz = 7^ sin ар. Используя формулу для прогиба консольной балки, нагруженной сосредоточенной силой на конце (см. табл. 9.2), найдем составляющие v и w полного прогиба / (рис. 12.7, в):
Подставив числовые значения величин, входящих в эти формулы, найдем v = 0,667 см, w = 1,540 см. По формулам (12.10) определим полный прогиб / = 1,678 см и его направление:
Из сравнения этого равенства с (12.6) следует, что | оу | = | сх01, то есть при плоском косом изгибе полный прогиб / направлен перпендикулярно к нулевой линии и изогнутая ось балки не расположена в силовой плоскости.
Пример 12.2. Стальная двутавровая балка сечением ~Llla (рис. 12.8) нагружена в главных плоскостях инерции Оху и Oxz сосред оточенным моментом М= 60 кНм и силой Р = 10 кН (заданы расчетные значения нагрузок). Расчетное сопротивление стали R = 210 МПа, коэффициент условий работы ус = 1.
Построим эпюру нормальных напряжений для опасного сечения и проверим прочность балки.
Рис. 12.8
Моменты инерции и моменты сопротивления сечения 127 а равны: Jz = 5500 см4; Jy = 337 см4; Wz = 407 см3; Wy = 50 см3.
На рис. 12.8, 6 построены эпюры изгибающих моментов Mz и Му. Наибольшие величины моменты Л/ и М имеют соответственно в сечениях CuD балки. Поэтому необходимо проверить прочность балки по формуле (12.8) в обоих сечениях.
В сечении С М = 45 кНм, Му = 2,5 кНм,
В сечении D Мг~ 15кНм, Му = 7,5 кНм,
Условие прочности в обоих сечениях выполняется. Более опасным является сечение D. Для построения эпюры напряжений в этом сечении определим по формулам (12.3) и (12.6) положения силовой и нулевой линий:
Так как > 0, то согласно введенному правилу знаков для угла ар силовая линия проходит через первую и третью четверти осей координат, а нулевая линия — через вторую и четвертую четверти. Эпюра нормальных напряжений для сечения D балки показана на рис. 12.8, в.
Источник