Уравнение совместности перемещений при растяжении
Конструкции, усилия в элементах которых не могут быть найдены из одних лишь уравнений равновесия, называются статически неопределимыми, а задачи определения усилий в таких системах называются статически неопределимыми задачами.
Степенью статической неопределимости называется разность между числом искомых неизвестных усилий и числом всех независимых уравнений равновесия, которые для этой системы можно составить.
Рис. 2.28
Рис. 2.29
Например, трехстержневая система (рис. 2.28) один раз статически неопределима, так как для вычисления усилий в трех ее стержнях можно составить всего лишь два независимых уравнения равновесия узла А:
Двухстержневая ферма (рис. 2.29) является, очевидно, статически определимой, так как усилия в ее стержнях полностью определяются из одних лишь уравнений равновесия
Заметим, что при записи уравнений равновесия мы не учитываем изменение углов между направлением сил вызванные деформацией фермы. Объясняется это тем, что при малых деформациях (а именно такие деформации, как правило, и рассматриваются в сопротивлении материалов) углы между стержнями фермы изменяются весьма незначительно и тем более незначительно изменяются тригонометрические функции этих углов. В этом проявляется принцип, называемый в сопротивлении материалов принципом сохранения начальных размеров. Согласно этому принципу в случае малых деформаций при составлении уравнений равновесия конструкцию можно рассматривать как жесткую, имеющую первоначальные размеры и форму. Этот принцип, естественно, не справедлив при больших деформациях.
Неопределенность рассматриваемых задач объясняется наличием в статически неопределимых системах избыточных или, иначе, лишних связей, не являющихся безусловно необходимыми для восприятия нагрузки. Так, в трехстержневой ферме можно удалить один из стержней, но она будет способна воспринимать нагрузку, оставаясь геометрически неизменяемой. Однако удалить одновременно два стержня нельзя, так как ферма станет геометрически изменяемой, подвижной системой. Следовательно, эта ферма имеет одну
избыточную связь. Отмеченное свойство является общим для любых статически неопределимых систем — степень статической неопределимости всегда равна числу лишних связей.
Статически неопределимые задачи не имеют решения, если считать материал абсолютно твердым, и имеют вполне определенное решение, если учитывать упругие свойства материала. Записывая условия неразрывности деформированной системы, всегда можно составить необходимое число дополнительных уравнений, разрешающих статическую неопределимость задачи. Эти дополнительные уравнения должны описать единственно возможные соотношения между перемещениями точек деформированной системы при заданных нагрузках. Поэтому они называются уравнениями совместимости перемещений, или уравнениями совместимости деформаций.
Для составления уравнений совместимости перемещений полезно изобразить систему после деформации, а затем по чертежу установить соотношения между перемещениями одних ее сечений или узлов относительно других. Для наглядности эти перемещения, как и удлинения стержней, изображаются на чертеже в весьма увеличенном виде. В действительности удлинения стержней, изменение углов между ними и перемещения узлов системы обычно весьма малы. Например, удлинение стального стержня длиной 100 см и площадью сечения при растяжении силой в 104 Н будет составлять всего
т. е. удлинение в 2000 раз меньше длины этого стержня. Поэтому изображать эти удлинения приходится в утрированно увеличенном виде.
Представив вид системы после деформации, нетрудно составить уравнения совместности перемещений. Запишем, например, уравнение совместности деформаций для рассмотренной выше трехстержневой системы. Удлинение среднего стержня согласно рис. 2.28 равно перемещению узла А. Удлинение крайнего стержня можно найти графически, проведя дугу радиуса с центром в точке В. Вследствие малости деформаций дугу этой окружности можно заменить перпендикуляром, опущенным из точки А на новое положение стержня. Рассматривая прямоугольный треугольник (на рис. 2.28 заштрихован), находим связь между удлинениями стержней 1 и
Изменением угла а пренебрегаем, так как оно незначительно. Переходя по закону Гука от удлинений стержней к искомым усилиям в них, получаем
Решая совместно уравнения равновесия и уравнение совместности перемещений, находим усилия в стержнях фермы.
Рис. 2.30
Рис. 2.31
При составлении уравнений совместности перемещений и записи уравнений равновесия необходимо обращать внимание на соответствие направлений искомых усилий представленному на чертеже характеру деформации (растяжение или сжатие) каждого стержня системы.
Отличительной особенностью любых статически неопределимых систем является зависимость распределения усилий по элементам системы от соотношения жесткостей этих элементов. Например, при сжатии медного цилиндра и стальной трубы между плитами пресса (рис. 2.30) доля сжимающего усилия Р, приходящаяся на цилиндр и трубу, зависит от соотношения их жесткостей
Для доказательства определим сжимающие усилия в трубе и цилиндре Рассекая цилиндр и трубу плоскостью, нормальной их оси, и рассматривая равновесие отсеченной части (см. рис. 2.30), получаем
Уравнением совместимости деформаций является равенство укорочений трубы и цилиндра
Решая систему уравнений равновесия и совместности деформаций, находим нормальные силы в сечениях трубы и цилиндра
Из этих формул видно, что с увеличением жесткости трубы при одновременном уменьшении жесткости цилиндра нормальные силы в ее сечениях возрастают, а в сечениях цилиндра уменьшаются, и, наоборот, при увеличении жесткости цилиндра возрастает доля воспринимаемой им нагрузки.
Таким образом, изменяя соотношение жесткостей элементов статически неопределимой системы, конструктор может по своему усмотрению уменьшать нагрузку на одни элементы за счет увеличения ее на других элементах.
Пример. Найти усилия в стержнях симметричной фермы, нагруженной силой Р (рис. 2.31), если материал и площади сечений всех стержней одинаковы. Определить необходимую площадь сечения стержней и перемещение узла А при и коэффициенте запаса прочности по пределу текучести Стержни выполнены из конструкционной малоуглеродистой стали 3.
Решение. При нагружении фермы стержни растягиваются, узел А смещается вниз и давит на стержень 3, вызывая растяжение стержней 4 и 5 и перемещение узла В. Очевидно, перемещение 6 узла А больше, чем смещение узла В, и их разность равна абсолютной величине сжатия стержня 3:
Это и есть уравнение совместности деформаций для данной фермы. Выражая перемещения узлов через удлинения стержней (см. заштрихованные треугольники на рис. 2.31), получаем
Переходя далее по закону Гука от удлинений к искомым усилиям в стержнях и учитывая, что записываем уравнение совместности так:
Направляя усилия в стержнях соответственно характеру деформации каждого стержня (см. рис. 2.31), составляем уравнения равновесия узлов А и В:
Решая систему уравнений равновесия и совместности деформаций, находим искомые усилия в стержнях:
усилия оказались с положительными знаками. Это означает, что стержни 1, 2, 4 и 5 действительно растянуты, а стержень 3 сжат. В соответствии с принятым правилом знаков для нормальных сил усилию в третьем стержне Должен быть приписан минус. Подставляя численное значение нагрузки Р, имеем
Необходимую площадь сечения стержней найдем по величине наибольшего усилия . Согласно условию прочности,
Предел текучести стали Следовательно, искомая площадь Принимаем
Перемещение узла А при см:
Пример. Определить усилия в стержнях и перемещение точки приложения силы Р (рис. 2.32). Диск рассматривать как абсолютно жесткий.
Решение. Данная система один раз статически неопределима, так как для определения усилий и в стержнях имеем одно только уравнение равновесия в которое не входили бы не интересующие нас по условию задачи опорные реакции
Рис. 2.32
Представим характер деформации системы. При приложении силы Р диск повернется вокруг неподвижной точки С, а шарниры А и В переместятся по дугам и окружностей с радиусами Вследствие малости деформаций эти дуги можно заменить их хордами и (см. рис. 2.32).
При вращении диска перемещение его точек пропорционально их расстояниям от центра вращения. Поэтому
где
Следовательно,
Это соотношение является уравнением совместности перемещений для данной системы.
Найдем связь между удлинениями стержней и перемещениями Для этого опустим из точек А и В перпендикуляры на исходные положения стержней. Из прямоугольных треугольников (см. рис. 2.32) получаем
Здесь
Подставив эти соотношения в уравнение совместности перемещений, выразим его через искомые усилия
Направляя усилия в стержнях в соответствии с характером их деформации, составляем уравнение равновесия диска:
Решая совместно уравнение совместности перемещений и уравнение равновесия, находим
Усилия надо приписать знак минус, так как решение подтверждает, что стержень 2 сжат. Окончательно
Рис. 2.33
Точка приложения силы Р смещается в направлении нормали к линии а величина смещения в два раза меньше
Пример, Построить эпюры а и 5 для стального бруса, нагруженного равномерно распределенной нагрузкой интен сивности и сосредоточенной силой (рис. 2.33). Определить запас прочности бруса, если см и а предел текучести материала
Решение. Данный брус представляет собой один раз статически неопределимую систему, так как для определения его двух опорных реакций и (показаны на рис. 2.33 пунктиром) можно записать всего одно независимое уравнение равновесия:
К составлению уравнения совместности перемещений можно подойти различными путями. Поступим так: отбросим одну из опор, например правую, и заменим ее действие неизвестной пока силой
Полученная система (см. рис. 2.33) . будет эквивалентна данной, если перемещение сечения В относительно А в этой системе, как и в данной, будет равно нулю: Из этогоусловия определяется искомая опорная реакция -Перемещение равно сумме удлинений всех трех участков бруса. Следовательно,
Определяя далее методом сечений нормальные силы в текущих сечениях каждого участка и вычисляя удлинения этих участков по формулам (2.13) и (2.14), получаем
и
Отсюда
Изложенный здесь прием раскрытия статической неопределимости называется методом сил. Итак, нормальные силы в сечениях бруса
а нормальные напряжения в тех же текучих сечениях
Перемещения сечений бруса будем отсчитывать от правого неподвижною сечения. Тогда
При отсчете от левого неподвижного сечения эпюра будет такой, как показано на рис. 2.33. Из эпюры о видно, что наибольшего значения напряжения достигают в конечном сечении первого участка и в сечениях третьего участка, но они различны по знаку. Сталь 45 одинаково работает на растяжение и сжатие. Поэтому все эти сечения равноопасны (для хрупкого материала опасными были бы сечения третьего участка, где действуют растягивающие напряжения). Подсчитывая максимальное напряжение и зная предельное напряжение для материала находим запас прочности бруса
Усилия в элементах статически неопределимых систем могут возникать не только от внешних сил, но и от температурного воздействия, а при сборке — и от неточности изготовления деталей конструкций. При совместном воздействии указанных факторов удобно воспользоваться принципом независимости действия сил и находить усилия в элементах конструкции суммированием усилий от каждого воздействия в отдельности.
Источник
3.1. Внутренние усилия и напряжения при растяжении (сжатии)
Растяжение (сжатие) – простой вид сопротивления, при котором стержень нагружен силами, параллельными продольной оси стержня и приложенными в центр тяжести его сечения. 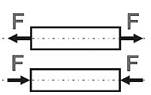
Рассмотрим стержень упруго растянутый центрально приложенными сосредоточенными силами F.

Прежде чем перейти к исследованию внутренних усилий и напряжений, возникающих в растянутом стержне, рассмотрим некоторые гипотезы, связанные с характером деформирования такого стержня и имеющие в сопротивлении материалов исключительно важное значение.
Принцип Сен-Венана: в сечениях, достаточно удаленных от мест приложения сил, распределение напряжений и деформаций мало зависит от способа приложения нагрузок.
Принцип Сен-Венана дает возможность вести расчет без учета местных (локальных) деформаций, возникающих вблизи от точек приложения внешних сил (см. рисунок) и отличающихся от деформаций основного объема материала, что в большинстве случаев упрощает решение задачи.
Гипотеза плоских сечений (гипотеза Я. Бернулли): поперечные сечения стержня плоские и перпендикулярные его оси до деформации остаются плоскими и перпендикулярными оси и после деформации (см. рисунок).
Используя метод мысленных сечений, определим внутренние усилия в растянутом стержне:
а) стержень, нагруженный растягивающими
силами F и находящийся в равновесии, рассекаем произвольным сечением;
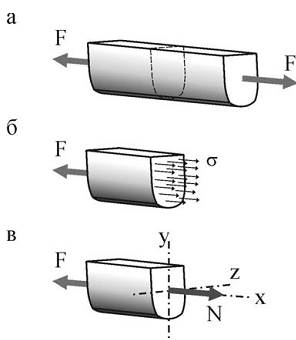
б) отбрасываем одну из частей стержня, а ее действие на другую часть компенсируем внутренними усилиями, интенсивностью σ;
в) осевое внутреннее усилие N, возникающее в сечении стержня, определим, составляя уравнения равновесия для отсеченной части:
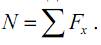
Проецируя внешнюю силу F, действующую на отсеченную часть стержня, на другие оси (y и z), а также составляя уравнения моментов относительно координатных осей, легко убедится, что осевое усилие N является единственным внутренним усилием, возникающим в сечении стержня (остальные тождественно равны нулю).
Таким образом, при растяжении (сжатии) из шести внутренних усилий в сечении стержня возникает только одно – осевое усилие N.
Нормальные напряжения σx, возникающие в сечении стержня, связаны с осевым усилием N следующим образом:
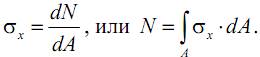
Учитывая, что в соответствии с гипотезой Бернулли напряжения равномерно распределены по поперечному сечению (т. е. σx=const), можно записать:
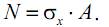
Таким образом, нормальные напряжения при растяжении (сжатии) определяются как
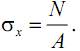
3.2. Перемещения и деформации при растяжении (сжатии)
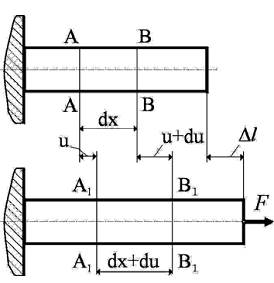
Рассмотрим стержень, находящийся под действием растягивающей нагрузки. Выделим (до деформации) два произвольных сечения стержня А–А и B–B, отстоящие друг от друга на расстоянии dx. От приложенной нагрузки сечение А–А переместиться в положение А1–А1 на расстояние u, а сечение B–B – в положение B1–B1 на расстояние u+du (du – бесконечно малая величина). Следовательно, абсолютное удлинение отрезка dx равно разности его размеров до и после деформации 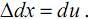
Относительная продольная деформация точек сечения A–A стержня при растяжении
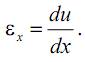
Для линейно-упругого материала относительная деформация при растяжении связана с нормальными напряжениями по закону Гука:
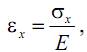
или, учитывая, что 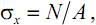
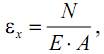
здесь Е – модуль нормальной упругости (модуль Юнга), постоянный коэффициент, который является конста нтой материала (например, для стали Е=2·1011Па, для меди Е=1·1011Па, для титана Е=1,2·1011Па).
Исходя из этих формул, можно записать выражение для перемещенийточек растягиваемого стержня в рассматриваемом сечении
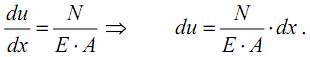
Тогда, полное удлинение стержня при растяжении ∆l, равное перемещению точек правого крайнего сечения, относительно левого крайнего:
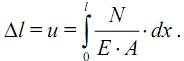
При постоянстве величин N, А, E вдоль оси стержня, абсолютное удлинение можно найти так:
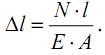
При растяжении стержень деформируется не только в продольном направлении, но и в поперечном.
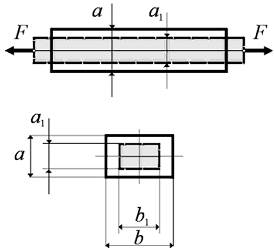
Абсолютная поперечная деформация стержня определяется как разность его поперечных размеров до и после деформации:

Относительная поперечная деформациястержня определяется отношением абсолютной поперечной деформации к соответствующему первоначальному размеру.
Относительная поперечная деформация при растяжении (сжатии) для изотропных материалов во всех направлениях одинакова:
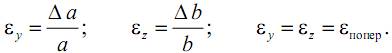
Между поперечной и продольной относительной деформациями при растяжении (сжатии) в пределах применимости закона Гука существует постоянное соотношение, которое называется коэффициентом поперечных деформаций (коэффициентом Пуассона µ).
Коэффициент Пуассона равен абсолютной величине отношения поперечной деформации к продольной
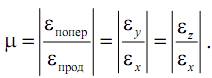
Коэффициент Пуассона – безразмерная величина.
Так как продольная и поперечная деформация для большинства конструкционных материалов имеют противоположные знаки, можем записать
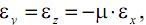
или, учитывая, что, согласно закону Гука,
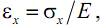
запишем
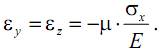
Коэффициент Пуассона µ наряду с модулем Юнга E характеризуют упругие свойства материала. Для изотропных материалов коэффициент Пуассона лежит в пределах от 0 до 0,5 (пробка µ≈0; сталь µ≈0,3; каучук µ≈0,5).
3.3. Расчеты на прочность и жесткость при растяжении (сжатии)
Одна из основных задач сопротивления материалов – обеспечить надежные размеры деталей, подверженных тому или иному силовому, температурному или другому воздействию. Указанные размеры можно определить из расчета на прочность или жесткость. Рассмотрим условия прочности и жесткости для случаев простого растяжения (сжатия). Опасность наступления разрушения характеризуется величинами наибольших нормальных и касательных напряжений, возникающих при нагружении в опасных (т. е. наиболее напряженных) точках сечения. Очевидно, что реальные материалы не могут выдерживать сколь угодно большие напряжения. Поэтому величины наибольших напряжений из условия надежности работы детали необходимо ограничивать некоторыми допустимыми значениями, такими, чтобы деталь испытывала только упругие деформации. Их называют допускаемыми напряжениями . При растяжении и сжатии допускаемые напряжения обозначают [σ+], [σ–] соответственно (принято также обозначение σadm).
Если из расчета известны максимальные и минимальные (по алгебраической величине) напряжения, возникающие в опасном сечении детали, то условия прочности могут быть записаны следующим образом:
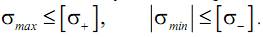
Если материал одинаково сопротивляется растяжению и сжатию, что характерно для пластичных материалов (более строго–для материалов в пластичном состоянии), а значит [σ+]=[σ–]=[σ], то
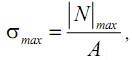
и условие прочности при растяжении (сжатии) запишем в виде:
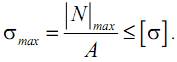
В некоторых случаях для обеспечения нормальной работы машин и сооружений размеры их деталей нужно выбирать так, чтобы обеспечивалось условие жесткости , то есть ограничить предельные деформации (перемещения) элементов конструкции.
Условие жесткости, ограничивающее изменение длины элемента, имеет следующий общий вид:
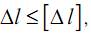
где ∆l – изменение размеров детали; [∆l] – допускаемая величина этого изменения.
Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин ∆l по участкам
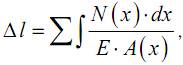
условие жесткости при растяжении (сжатии) запишем следующим образом:
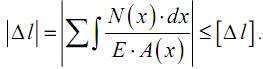
3.4. Допускаемые напряжения. Коэффициент запаса прочности. Виды расчетов
Итак, размеры деталей необходимо подбирать таким образом, чтобы под действием приложенных нагрузок элемент конструкции не разрушался и не получал деформаций, превышающих допустимые. Отметим при этом, что в большинстве машиностроительных деталей не допускается возникновение остаточных деформаций под действием эксплуатационных нагрузок.
Как показывают механические испытания (испытания на растяжение и сжатие), раз рушен и е хрупких материалов начинается, когда напряжения в сечении элемента конструкции превысят величину временного сопротивления (предела прочности) σв. Поэтому для хрупких материалов, деформация которых, как правило, незначительна, за опасное (предельное) напряжение следует принимать именно предел прочности σв:
σ =σ .
Для пластичных материалов за опасное (предельное) напряжение следует принимать предел текучести σт (или условный предел текучести σ0,2, если площадка текучести отсутствует), так как за пределом текучести в пластичных материалах возникают значительные пластические деформации, приводящие при сбросе нагрузки до нуля к появлению остаточных напряжений, следовательно:
σ =σ .
Естественно, что эти опасные напряжения не могут быть использованы в качестве допускаемых. Их следует уменьшить настолько, чтобы в эксплуатационных условиях действующие напряжения гарантированно были меньше опасных, а деформации были упругими. Таким образом, допускаемое напряжение может быть определено по формуле
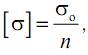
где σо – опасное напряжение; n – коэффициент запаса прочности.
Допускаемые напряжения – это наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы.
Выбор коэффициента запаса прочности зависит от состояния материала
(хрупкое или пластичное), характера приложения нагрузки (статическая, динамическая или повторно-переменная) и некоторых общих факторов, основными из которых являются:
1) различие механических характеристик материала в лабораторных образцах и реальной детали;
2) неточность задания величины внешних нагрузок;
3) неточность расчетных схем и приближенность методов расчета;
4) учет конкретных условий работы рассчитываемой конструкции;
5) долговечность и значимость проектируемого сооружения или машины.
Для конструкционных сталей значение коэффициента запаса прочности принимается n=1,4…1,6; для хрупких материалов n=2,5…3; для древесины n=3,5…6. Тогда величина допускаемых напряжений для среднеуглеродистых сталей [σ]=140…180 МПа; для высоколегированных [σ]=200…400 МПа.
Используя условие прочности, можно решать три типа задач:
1) проектировочный расчет – по известным нагрузкам для известного материала найти надежные с точки зрения прочности размеры поперечного сечения стержня (спроектировать прочную деталь);
2) проверочный расчет – по заданным размерам и материалу детали проверить, может ли она выдержать приложенную нагрузку;
3) расчет по несущей способности (грузоподъемности) – по известным размерам детали, материалу и схеме нагружения определить допустимую величину нагрузки на деталь.
3.5. Понятие о концентрации напряжений
Равномерное распределение напряжений по сечению растянутого стержня сохраняется только в случае, если сечения стержня остаются постоянными по его длине. Резкие изменения площади поперечного сечения вследствие наличия поперечных отверстий, выточек, канавок, надрезов приводят к неравномерному распределению напряжений (вызывают концентрацию напряжений ) и называются концентраторами напряжений.
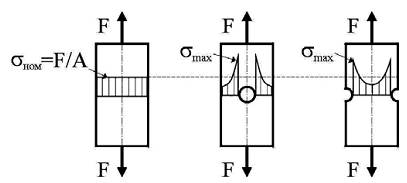
При исследовании явления концентрации напряжений вводят понятия номинального напряжения, наибольшего местного напряжения и коэффициента концентрации напряжений.
Номинальное напряжение – напряжение, вычисленное на основе предположения об отсутствии концентрации напряжений.
При растяжении номинальное напряжение вычисляется как
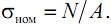
Наибольшее местное напряжение – максимальное напряжение, действующее в месте концентрации напряжений.
Местные напряжения, действующие в области концентратора напряжений, могут быть найдены теоретически – методами теории упругости, либо экспериментально – непосредственным измерением при помощи специальных приборов и методик.
Коэффициент концентрации напряжений – отношение максимального местного напряжения к номинальному напряжению
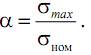
Коэффициент концентрации зависит от вида концентратора, размеров и формы образца, а также свойств материала.
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ПРИ РАСТЯЖЕНИИ И СЖАТИИ
4.1. Основные сведения о статически неопределимых системах
В инженерной практике часто встречаются системы, в которых число наложенных связей больше числа уравнений равновесия. В этих системах, используя только уравнения равновесия, невозможно определить ни усилия в связях (реакции опор), ни внутренние усилия, возникающие в элементах конструкций. Такие системы называют статически не определимыми.
Статически неопределимые системы – это упругие стержневые системы (конструкции), в которых количество неизвестных внутренних усилий и реакций опор больше числа уравнений статики, возможных для этой системы.
Кроме уравнений статики для расчета таких систем (конструкций) приходится привлекать дополнительные условия, описывающие деформацию элементов данной системы. Их условно называют уравнениями перемещений или уравнениями совместности деформаций (а сам метод решения иногда называют методом сравнения деформаций).
Степень статической неопределимости системы – это разность между числом неизвестных и числом независимых уравнений равновесия, которые можно составить для данной системы.
Количество дополнительных уравнений перемещений, необходимых для раскрытия статической неопределимости, должно быть равно степени статической неопределимости системы.
4.2. Порядок решения статически неопределимых задач
Статически неопределимые конструкции будем рассчитывать, решая совместно уравнения, полученные в результате рассмотрения статической, геометрической и физической сторон задач. При этом будем придерживаться следующего порядка:
1. Статическая сторона задачи. Составляем уравнения равновесия отсеченных элементов конструкции, содержащие неизвестные усилия. Определяем степень статической неопределимости.
2. Геометрическая сторона задачи. Рассматривая систему в деформированном состоянии, устанавливаем связи между деформациями и перемещениями отдельных элементов конструкции и записываем уравнения совместности деформаций (уравнения перемещений).
3. Физическая сторона задачи. На основании закона Гука выражаем перемещения или деформации элементов конструкции через действующие в них неизвестные (пока) усилия.
4. Математическая сторона задачи (синтез). Решая совместно статические, геометрические и физические уравнения, находим неизвестные усилия.
Рассмотрим примеры расчета некоторых простейших статически неопределимых конструкций.
4.3. Примеры решения статически неопределимых задач
Источник
