Сопромат эпюр перемещений растяжение
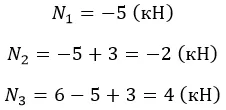
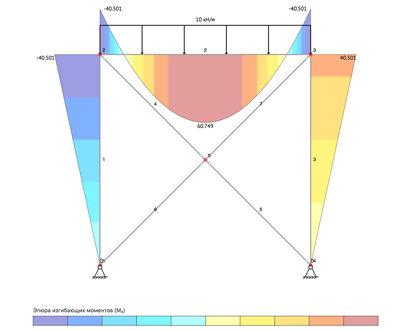
Расчет рамы/фермы
Расчет
статически-неопределимых систем
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
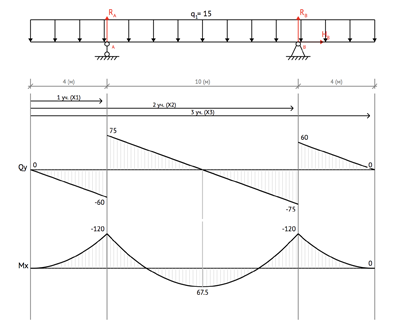
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
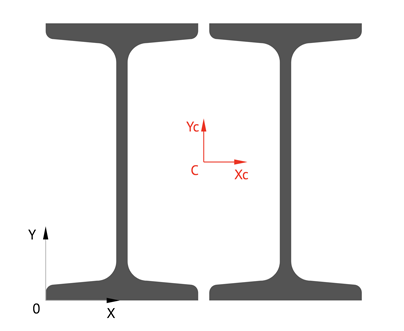
Расчет
геометрических характеристик поперечного сечения
Определение
центра тяжести, моментов инерции, моментов сопротивления
Формирование
подробного отчета
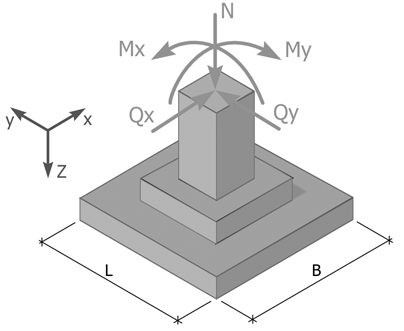
Расчет
столбчатого фундамента
Расчет
ленточного фундамента
Формирование
подробного отчета
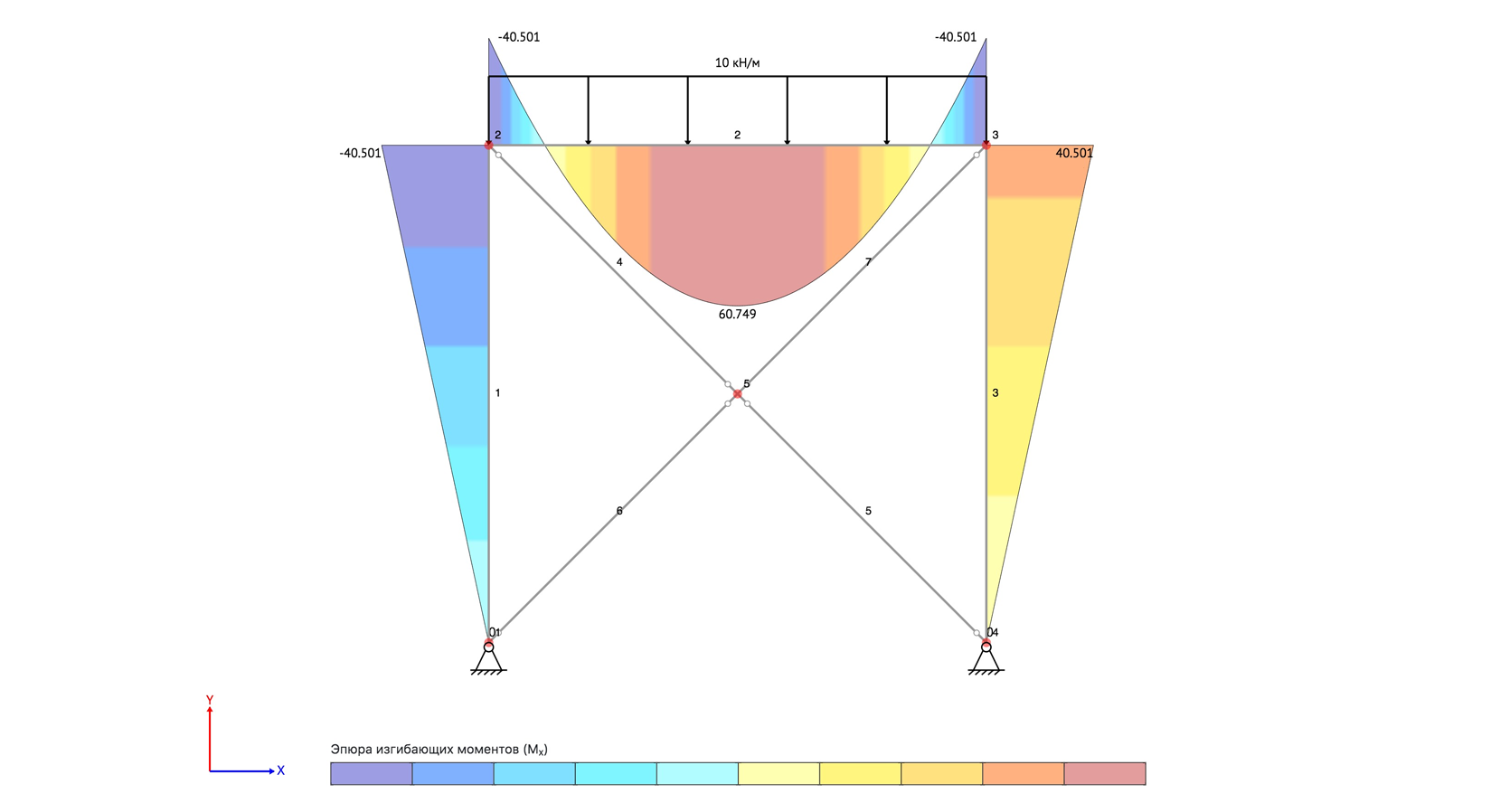
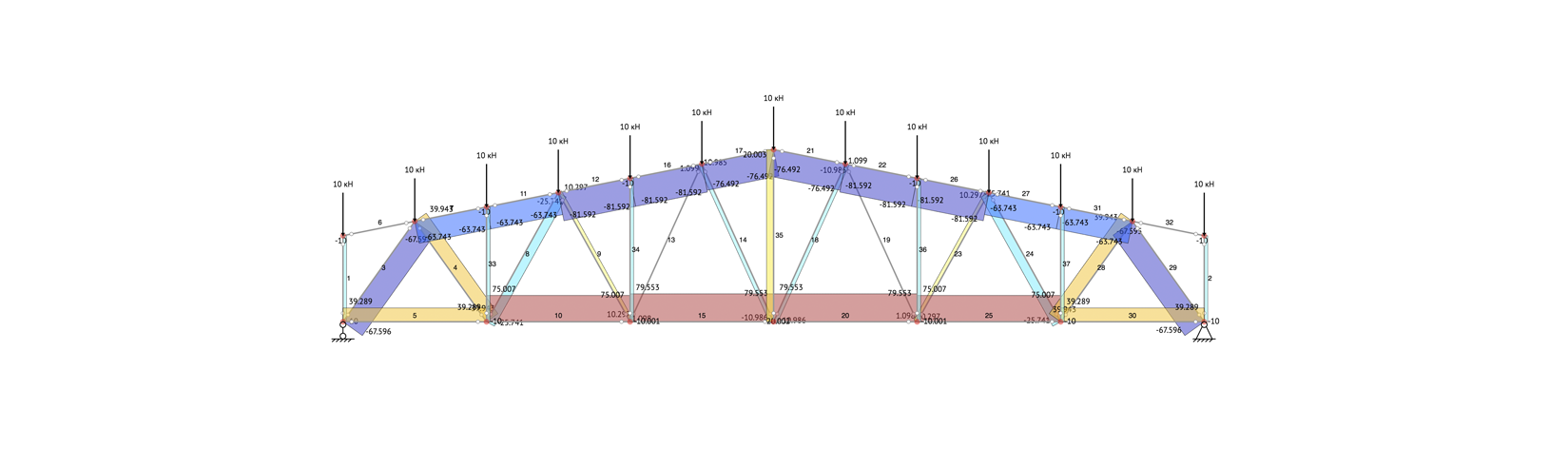
Расчет
статически-неопределимых систем
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
Источник
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
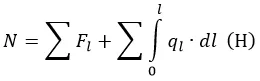
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
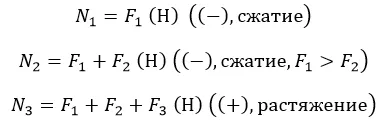
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
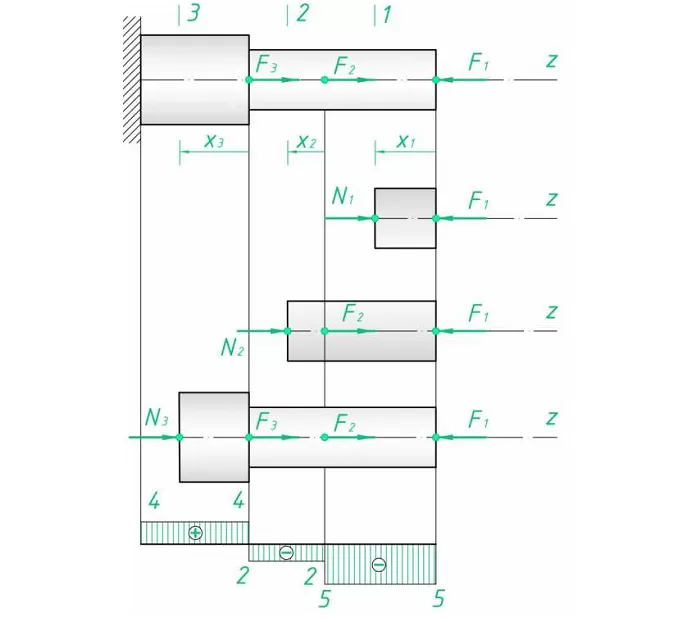
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
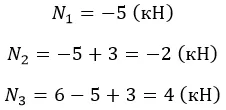
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
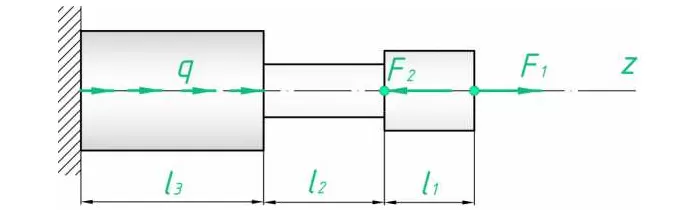
Рис. 2
Дано:
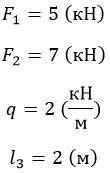
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
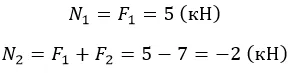
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
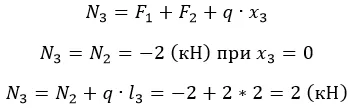
По полученным данным строим эпюру (рис. 3).
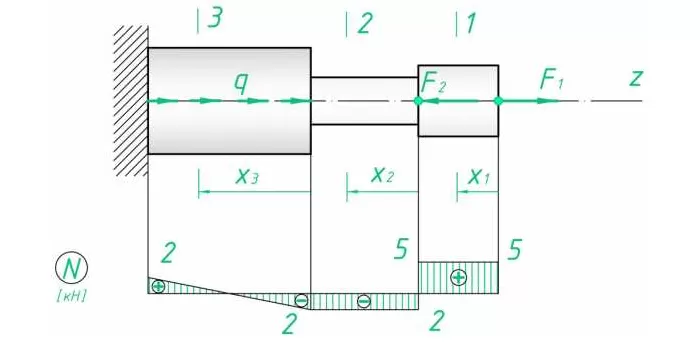
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
1. На рисунке проводиться ось ОХ, совпадающая с продольной осью стержня.
2. Под рисунком стержня проводятся две базовые нулевые линии, параллельно продольной оси стержня. Одна для эпюры продольной силы Nz
Вторая базовая нулевая линия для эпюры нормальных напряжений (Мпа).
3. Стержень разбивается на участки. Для границ участков проводятся вертикальные линии в точках приложения нагрузки и изменения площади поперечного сечения вниз до пересечения с базовыми нулевыми линиями. Нумерация участков начинается со свободной стороны стержня для задачи статически определимой. Если задача статически неопределимая, то нумерация выполняется слева направо.
4. Для определения значения продольной силы используется метод сечений. В середине участка проводится сечение. Указывается направление продольной силы. Положительным считается направление продольной силы, направленной от сечения (растягивает). Значение продольной силы Nz определяется из условия равновесия отсечённой части (сумма проекций на ось ох всех действующих сил равна нулю 0).
5. Вычисляем значение нормальных напряжений.
6. Положительные значения продольной силы и нормального напряжения откладываем вверх от базовой нулевой линии, отрицательные вниз.
7. Проверяем правильность решения задачи по эпюре продольной силы. В точках, где приложена сосредоточенная сила, на эпюре должен быть скачок равный значению продольной силы.
8. Условие прочности проверяем по эпюре нормальных напряжений. Максимальные напряжения, возникающие в конструкции, не должны превышать допускаемых.
Пример №1: Построить эпюры продольной силы N и нормального напряжения σ, проверить на прочность стальной стержень, закрепленный с одной стороны (статически определимая задача). Р1 = 10кН Р2 = 15кН
Р3 =15кН
=100 Мпа; А1 = F; А2 = 2F; F = 100 мм2
Решение:
Параллельно продольной оси стержня проводим две базовые нулевые линии для продольной силы и нормального напряжения.
Разбиваем стержень на участки, начиная со свободной стороны. Проводим вниз вертикальные линии в точках приложения сил и изменения площади поперечного сечения до пересечения с нулевыми линиями. Нумерация участков начинается со свободной стороны стержня.
1 участок:
— на первом участке проводим сечение, перпендикулярное продольной оси, мысленно отбрасываем большую часть и рассматриваем меньшую часть стержня. Заменяем действие отброшенной части на оставленную продольной силой N1. Положительным считается действие от сечения (растягивает).
Рассматриваем равновесие оставленной части, проецируя действующие силы на ось ОХ:
Определяем продольную силу на первом участке:
-N1+ Р1=0 следовательно N1 = Р1=10 кН
Определяем нормальное напряжение на первом участке
2 участок:
-N2+ Р1 — Р2=0 следовательно N2 = Р1-Р2 =10-15= -5 кН
3 участок:
-N3+ Р1 — Р2=0 следовательно N3 = Р1-Р2 =10-15= -5 кН
4 участок:
-N4+ Р1 — Р2+Р3=0 следовательно N4 = Р1-Р2+Р3=10-15+15= 10 кН
Рис. 10.
Метод сечений для определения продольной силы.
Для построения эпюр продольной силы и нормального напряжения задаёмся произвольным масштабом (например: одна клеточка -5 кН и -25 мегапаскалей). Строим эпюры продольной силы и нормального напряжения, откладывая положительные значения вверх от базовой нулевой линии, отрицательные вниз.
Проверяем правильность решения задачи по эпюре продольной силы, в точке приложения сосредоточенной силы на эпюре должен быть скачок, равный действующей силе.
По эпюре нормального напряжения проверяем условие прочности максимальные напряжения должны быть меньше или равны допустимым, значит прочность обеспечена.
Рис.11.
Эпюры продольной силы N и нормального напряжения σ.
СПИСОК ЛИТЕРАТУРЫ
1. Рубашкин А.Г. Лабораторные работы по сопротивлению материалов.- М.: Высшая школа, 1961.-159с.
2. Афанасьев A.M., Марьин В.А. Лабораторный практикум по сопротивлению материалов.- М.: Наука, 1975.-284с.
3. Феодосьев В.И. Сопротивление материалов.- М.: Наука, 1979.-559с.
4. Писаренко Г.С. Сопротивление материалов.- Киев.: Высшая школа, 1973.-667с.
Источник
+- мdA
площадь сечения стержняZB м м м м м м м м м м м м м м м м м м м м м м м м м м м м мL=2(м)N[кН]
Продольная сила N,кН0σ [МПа]
Напряжения ,МПа0δ [мм]
Перемещения характерных сечений ,мм0
Модуль упругости E=
ГПа (сталь)
Выбрать из таблицы
Длина стержня l=
м.
Площадь A= = 0.0004 м2
Выбрать тип сечения исходя из условий задачи
Круг
Квадрат
Прямоугольник
Шестигранник
Кольцевое сечение (труба)
Площадь сечения в см2:
A = π · d2/4
= 3.14·(d·0.1)2/4 =
[см2]
Масса 1 м профиля, [кг]:
m = ρ·A·L =
7850· A ·1/10000 = [кг]
ДСТУ 4738:2007/ГОСТ 2590-2006 Прокат сортовой стальной горячекатаный круглый.
(При вычислении массы 1 м проката плотность стали принята равной 7850 кг/м3)
Выбрать диаметр из сортамента:
| Диаметр d, мм | |||||||||||||||||||
| 5 | 5.5 | 6 | 6.3 | 6.5 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |
| 42 | 43 | 44 | 45 | 46 | 47 | 48 | 50 | 52 | 53 | 54 | 55 | 56 | 58 | 60 | 62 | 63 | 65 | 67 | 68 |
| 70 | 72 | 73 | 75 | 78 | 80 | 82 | 85 | 87 | 90 | 92 | 95 | 97 | 100 | 105 | 110 | 115 | 120 | 125 | 130 |
| 135 | 140 | 145 | 150 | 155 | 160 | 165 | 170 | 175 | 180 | 185 | 190 | 195 | 200 | 210 | 220 | 230 | 240 | 250 | 260 |
| 270 | |||||||||||||||||||
ДСТУ ГОСТ 1535:2007/ГОСТ 1535-2006 Прутки медные
(При вычислении массы 1 м проката плотность меди принята равной 8900 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 24 | 25 | 27 | 28 | 30 | 32 | 33 | 35 | 36 | 38 | 40 | 41 | 45 | 46 | 50 | ||
| Номинальный диаметр d, мм | |||||||||||||||||||
| 20 | 22 | 25 | 28 | 30 | 32 | 35 | 38 | 40 | 42 | 45 | 48 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 |
| 90 | 95 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | |||||||||
ДСТУ ГОСТ 2060:2007/ГОСТ 2060-2006 Прутки латунные
(При вычислении массы 1 м проката плотность латуни принята равной 8500 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 30 | 32 | 35 | 36 | 38 | 40 | 41 |
| 42 | 45 | 46 | 48 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | 110 | 120 | 130 | 140 | 150 |
| 160 | 170 | 180 | |||||||||||||||||
ГОСТ 21488-97 Прутки прессованные из алюминия и алюминиевых сплавов
(При вычислении массы 1 м проката плотность алюминия принята равной 2700 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 8 | 10 | 12 | 14 | 16 | 18 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 90 |
| 100 | 110 | 120 | 130 | 140 | 150 | 160 | 180 | 200 | 250 | 300 | 350 | 400 | |||||||
ГОСТ 26492-85 Прутки катаные из титана и титановых сплавов
(При вычислении массы 1 м проката плотность титана принята равной 4500 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 10 | 12 | 14 | 16 | 18 | 20 | 22 | 25 | 28 | 30 | 32 | 35 | 38 | 40 | 42 | 45 | 48 | 50 | 52 | 55 |
| 60 | 65 | 70 | 75 | 80 | 85 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | |||||||
ТУ 48-19-39-85 Прутки вольфрамовые
(При вычислении массы 1 м проката плотность титана принята равной 19300 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 10.5 | 11 | 11.5 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | |||||||||||||||
ТУ 48-19-247-87 Прутки молибденовые диаметром от 16 до 125 мм
(При вычислении массы 1 м проката плотность молибдена принята равной 10188 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 16 | 17 | 18 | 19 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 |
| 52 | 54 | 56 | 58 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | 105 | 110 | 115 | 120 | 125 | ||
ГОСТ 13083-2016 Прутки из никеля и кремнистого никеля
(При вычислении массы 1 м проката плотность никеля принята равной 8900 кг/м3)
Выбрать диаметр из сортамента:
| Номинальный диаметр d, мм | |||||||||||||||||||
| 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | |||||
| Номинальный диаметр d, мм | |||||||||||||||||||
| 42 | 45 | 48 | 50 | 55 | 60 | 70 | 80 | 90 | |||||||||||
a
Площадь сечения в см2:
A = a2 = (a·0.1)2 =
[см2]
Масса 1 м профиля, [кг]:
m = ρ·A·L =
7850· A ·1/10000 = [кг]
(При вычислении массы 1 м проката плотность стали принята равной 7850 кг/м3)
ДСТУ 4746:2007/ГОСТ 2591-2006 Прокат сортовой стальной горячекатаный квадратный.
Выбрать размер из сортамента:
DAs
D=s/2 + (2A)/(πs)
Толщина стенки трубы s=
мм
Нормальные линейные размеры (диаметры, длины, высоты и др.) должны выбираться в соответствии с таблицей
(размеры в мм)
Выбрать размер из таблицы:
| Ra5 | |||||||||||||||||||
| 0,1 | 0,4 | 0,63 | 1,0 | 1,6 | 2,5 | 4,0 | 6,3 | 10,0 | 16,0 | 25 | 40 | 63 | 100 | 160 | 250 | 400 | 630 | 1000 | 1600 |
| Ra10 | |||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,4 | 0,5 | 0,63 | 0,8 | 1,0 | 1,2 | 1,6 | 2,0 | 2,5 | 3,2 | 4,0 | 5,0 | 6,3 | 8,0 | 10 | 12 | 16 | 20 | 25 | 32 | 40 | 50 | 63 | 80 | 100 | 125 | 160 | 200 |
| 250 | 320 | 400 | 500 | 630 | 800 | 1000 | 1250 | 1600 | 2000 | ||||||||||||||||||||
| Ra20 | |||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,4 | 0,5 | 0,63 | 0,71 | 0,8 | 0,9 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,5 | 2,8 | 3,2 | 3,6 | 4,0 | 4,5 | 5,0 | 5,6 | 6,3 | 7,1 | 8,0 | 9,0 | 10 | 11 | 12 |
| 14 | 16 | 20 | 22 | 25 | 28 | 32 | 36 | 40 | 45 | 50 | 56 | 63 | 71 | 80 | 90 | 100 | 110 | 125 | 140 | 160 | 180 | 200 | 220 | 250 | 280 | 320 | 360 | 400 | 450 |
| 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | |||||||||||||||||
| Ra40 | |||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,63 | 0,71 | 0,8 | 0,9 | 1,0 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | 2,1 | 2,2 | 2,4 | 2,5 | 2,6 | 2,8 | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 |
| 4,0 | 4,2 | 4,5 | 4,8 | 5,0 | 5,3 | 5,6 | 6,0 | 6,3 | 6,7 | 7,1 | 7,5 | 8,0 | 8,5 | 9,0 | 9,5 | 10,0 | 10,5 | 11,0 | 11,5 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 24 | 25 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 45 | 48 | 50 | 53 | 56 | 60 | 63 | 67 | 71 | 75 | 80 | 85 | 90 | 95 | 100 | 105 | 110 | 120 |
| 125 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 | 220 | 240 | 250 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 | 420 | 450 | 480 | 500 | 530 | 560 | 600 | 630 | 670 |
| 710 | 750 | 800 | 850 | 900 | 950 | 1000 | 1060 | 1120 | 1180 | 1250 | 1320 | 1400 | 1500 | 1600 | 1700 | 1800 | 2000 | ||||||||||||
| Дополнительные размеры | |||||||||||||||||||||||||||||
| 2,3 | 2,7 | 2,9 | 3,1 | 3,3 | 3,5 | 3,7 | 3,9 | 4,1 | 4,4 | 4,6 | 4,9 | 5,2 | 5,5 | 5,8 | 6,2 | 6,5 | 7,0 | 7,3 | 7,8 | 8,2 | 8,8 | 9,2 | 9,8 | 10,2 | 10,8 | 11,2 | 11,8 | 12,5 | |
| 13,5 | 14,5 | 15,5 | 16,5 | 17,5 | 18,5 | 19,5 | 20,5 | 21,5 | 23 | 27 | 29 | 31 | 33 | 35 | 37 | 39 | 41 | 52 | 55 | 58 | 65 | 70 | 73 | 78 | 82 | 88 | 92 | 98 | |
| 102 | 108 | 112 | 115 | 118 | 135 | 145 | 155 | 165 | 175 | 185 | 195 | 205 | 215 | 230 | 270 | 290 | 310 | 315 | 330 | 350 | 370 | 390 | 410 | 440 | 460 | ||||
