Разрушающее напряжение для материала изготовления при растяжении на изгибе

ЛЕКЦИЯ
4,5

Основными
механическими характеристиками
материалов являются:

—
разрушающее напряжение при сжатии σс;

—
разрушающее напряжение при растяжении
σр:

—
разрушающее напряжение при статическом
изгибе σи;

—
ударная вязкость а.

Все эти механические характеристики в
основном определяют конструкционную
прочность деталей машин и приборов по
отношению к действию механических
нагрузок в процессе эксплуатации.

Разрушающее
напряжение при сжатии σс
,(при испытании материалов эту
характеристику называют пределом
прочности при сжатии) определяют на
специальных образцах, имеющих форму
цилиндра или куба.

σс
= Pc/So
МПа,

где
РС-
разрушающее усилие при сжатии стандартного
образца.

Разрушающее
напряжение при растяжении
σр
(при испытании материалов эту характеристику
называют пределом прочности или временным
сопротивлением материала при растяжении.

σр=
Pp/Fo
МПа,

где
Рр
— разрушающее усилие при разрыве
стандартного образца.

Данную характеристику
определяют на специальных разрывных

машинахна стандартных
образцах такой формы, при которой
обеспечивается равномерное распределение
растягивающего усилия по площади сечения
образца в его средней части.

Разрушающее
напряжение при статическом изгибе σи(прииспытании

материалов эту
характеристику называют пределом
прочности при статическом изгибе).

σи
=1,5PиL/
bh
; σи=Wmax/
W,

где
Wmax
-максимальный изгибающий момент (Wmax
= Pmax
L/4).

W=b2h/
6 (для прямоугольного сечения).

W
= 3,14d3/32
(для образца круглого сечения).

Разрушающее напряжение для материала изготовления при растяжении на изгибе

Ударная
вязкость
«а» определяется как отношение работы
А, затраченной маятником испытательной
машины (копра) на разрушение специального
образца, к площади его поперечного
сечения Fo.

а=A/Fo
(Дж/м2)

Чем меньше ударная
вязкость, тем более хрупок материал.
Ударная вязкость определяется в
результате динамических испытаний
материалов при однократном нагружении.

Разрушающие
напряжения при сжатии растяжении и
статическом изгибе определяются в
результате испытаний материалов при
статическом однократном нагружении.

Наряду с рассмотренными
характеристиками и видами испытаний
материалов существуют и другие
характеристики и соответствующие им
специальные виды испытаний: циклические
испытания, специальные испытания на
жаростойкость, коррозионостойкость,
износостойкость, вибростойкость и др.,
которые позволяют определить функциональные
и

эксплуатационные
характеристики рассматриваемых
материалов. Более подробно закономерности,
определяющие строение и свойства
материалов в зависимости от их состава
и условий обработки рассматриваются в
спецдисциплине «Материаловедение».

ЭЛЕКТРИЧЕСКИЕ
ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ.

Основным свойством вещества по отношению
к электрическому полю является
электропроводностьт.е. способность
проводить электрический ток под
воздействием постоянного (не изменяющегося
во времени) электрического напряжения.
Любой электротехнический материал-
проводник, полупроводник и даже диэлектрик
— проводит электрический ток.

Если
вещество находится в электрическом
поле с напряженностью Е, то имеющиеся
в веществе свободные заряженные частицы
— носители
зарядов —
под действием силы F=qЕ,
где q-заряд
частицы, приобретают ускорение в
направлении вектора Е (для носителей,
имеющих положительный заряд «+q»)
или в противоположном направлении (для
носителей с отрицательным зарядом
«-q»). Возникающее таким образом
упорядоченное в пространстве (в отличие
от хаотического теплового) движение
электрических зарядов и есть электрический
ток в веществе.

Для
оценки степени электропроводности того
или иного материала необходимо
определить его удельное
электрическое
сопротивление
ρ

ρ=R
S/L;

где
R
-общее электрическое сопротивление
образца, Ом;

L
-длина пути тока в образце материала,
м;

S
-площадь сечения образца материала,
через которую протекают токи
проводимости, м2.

Величина,
обратная сопротивлению, называется
электрической
проводимостью.

γ= 1/ρ.

Проводимость
измеряется в сименсах, в честь немецкого
физика Сименса.

Удельная проводимость
и удельное сопротивление определяют
плотность тока в веществе при заданной
напряженности электрического поля,
т.е. количественно характеризуют явление
электропроводности.

Значения их у
различных электротехнического материалов
резко отличаются. У веществ в сверхпроводящем
состоянии удельное сопротивление
равно нулю, а у разреженных газов, при
отсутствии в них электрического разряда
стремится к бесконечности.

Удельное
сопротивление металлических проводников
очень мало (10-8…10-б
Ом м),
что указывает на большую электрическую
проводимость проводниковых материалов.
Удельное сопротивление полупроводниковых
материалов(полупроводников) больше,
чем проводников (10-4…108
Ом м),а
диэлектриков еще больше (108…1018
Ом м).

Большое удельное
сопротивление диэлектриков указывает
на их весьма малую проводимость.

Однако,
при классификации веществ по электрическим
свойствам (проводники, полупроводники,
диэлектрики), кроме значения ρ необходимо
учитывать и физическую природу
электропроводности, в частности, вид
свободных носителей заряда и характер
зависимости ρ от температуры. Необходимо
также иметь ввиду, что в зависимости от
структуры и внешних условий порядок
значений ρ вещества может различаться
весьма существенно. Так, углерод в
аллотропической модификации графита
— проводник, а в модификации алмаза —
диэлектрик; твердые и жидкие металлы
— проводники, но пары металлов —
диэлектрики; типичные (для нормальных
условий) полупроводники германий Ge
и кремний Si
при воздействии очень высоких

гидростатических
давлений становятся проводниками, а —
при воздействии

очень
низких температур — диэлектриками.

Зависимость
удельного электрического сопротивления
проводников, полупроводников и
диэлектриков от температуры может быть
представлена графически (рис.1).

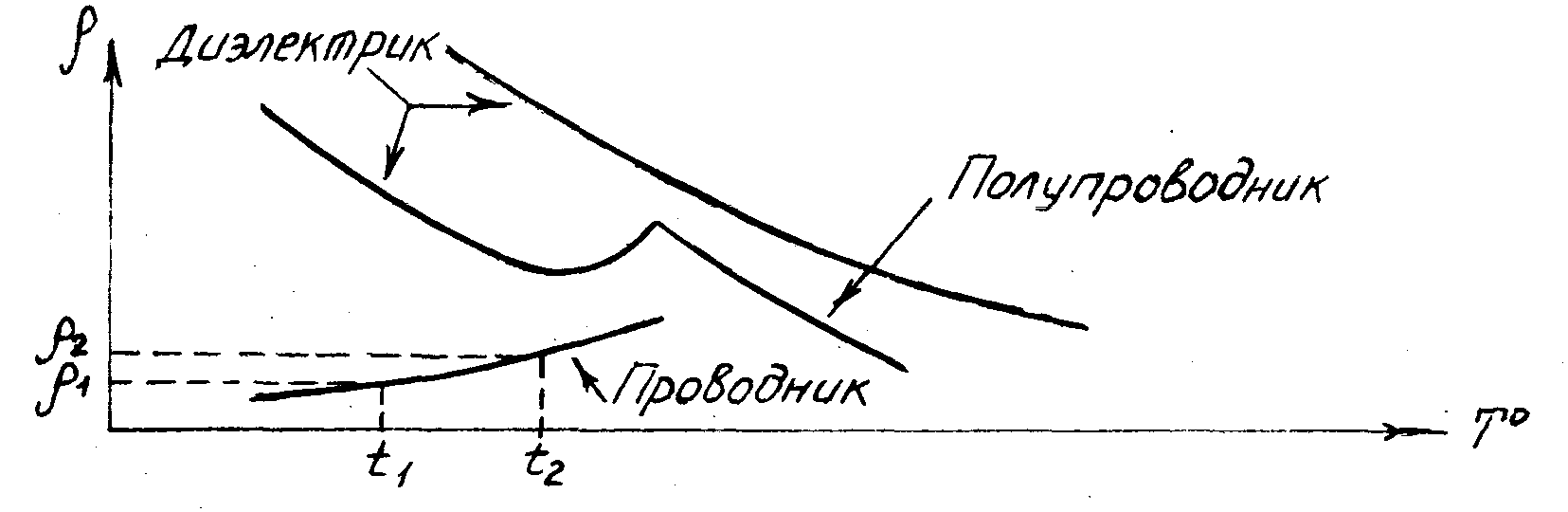
Разрушающее напряжение для материала изготовления при растяжении на изгибе

Рис. 1. Зависимость
ρ от температуры.

Температурный
коэффициент удельного сопротивления
ТКρ.

Эта
характеристика позволяет оценить
изменение удельного электрического
сопротивления материала при изменении
температуры. При линейном изменении
удельного сопротивления (в узком
диапазоне температур)

TKρ(α)=(p2-p1)/
[p1(t2-t1)];

здесь:
ρ1
и ρ2-удельные
электрические сопротивления материала
при начальной t1
и температуре t2.
Kaк
видно из рисунка 1,ТКρ
проводников больше нуля, что указывает
на рост электрического сопротивления
проводников с повышением температуры.
У полупроводников и диэлектриков
ТКρ
меньше нуля, что указывает на уменьшение
сопротивления этих материалов с
повышением температуры.

Диэлектрическая
проницаемость
εr.

Эта
характеристика позволяет определить
способность диэлектрика при нанесении
на него электродов и подаче напряжения
образовывать электрическую
емкость.

Электрическая
ёмкость “C”
плоского конденсатора с двумя
металлическими электродами
прямопропоциональна диэлектрической
проницаемости, т.е.

C=εo
*εr*
S/h,

где:
— h
-толщина диэлектрика, м;

—
S
-площадь одного металлического электрода,
м2;

—
εo-электрическая
постоянная (εo=8,85416*
10-12Ф/м);

—
εr-диэлектрическая
проницаемость.

Диэлектрическая
проницаемость электроизоляционных
материалов зависит от интенсивности
процессов поляризации,
протекающих в диэлектриках под действием
приложенного напряжения.

Различают четыре
основных вида поляризации диэлектриков:
электронную, дипольную, ионную и
спонтанную. Более подробно эти виды
будут рассмотрены при рассмотрении
свойств диэлектриков.

Диэлектрическая
проницаемость зависит от температуры.
График зависимости εr=f
(Т) проставлен на рис.2.

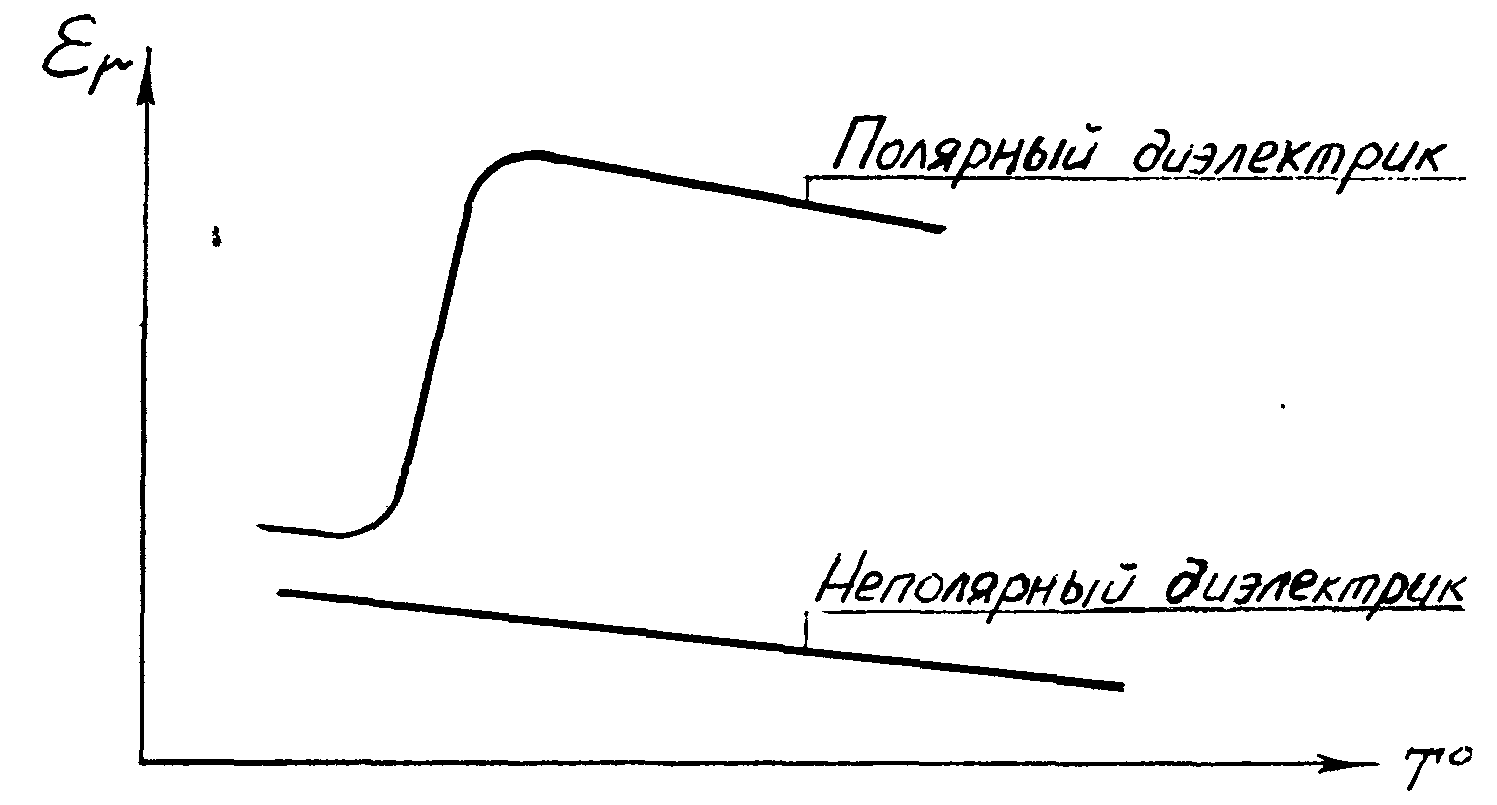Разрушающее напряжение для материала изготовления при растяжении на изгибе Рис.2.
Зависимость εr от Т .

Поскольку
в неполярных диэлектриках происходит
только электронная
поляризация,
их диэлектрическая проницаемость
невелика (1-2,2).В полярных диэлектриках
интенсивность поляризации больше, чем
в нейтральных, так как в них осуществляется
два вида поляризации: дипольная и
электронная, поэтому величина ε
составляет порядка 3-8.

Следует отметить,
что диэлектрическая проницаемость
электроизоляционных материалов
изменяется не только от температуры,
но и

от частоты
приложенного напряжения, давления,
влажности и др. факторов.

Тангенс
угла диэлектрических потерь tgδ.

При воздействии
электрического поля на любое вещество
в последнем наблюдается рассеяние
некоторого количества электрической
энергии, превращающейся в тепловую.
Обычно говорят о «потерях», имея
в виду среднюю за некоторый промежуток
времени рассеиваемую электрическую
мощность.

Если
к обрезку металлического проводника
подключить постоянное напряжение
или переменное, действующее значение
которого равно постоянному, то потери
энергии в том и другом случае будут
одинаковы, т.е. Р ==Р
~
.

Если
же такой опыт провести с диэлектриком,
то потери энергии в нем при переменном
напряжении будут во много раз больше
потерь энергии при постоянном напряжении,
т. e.P~»P=.
Потери энергии в диэлектрике называются
диэлектрическими
потерями
(активная мощность). В диэлектрике,
помещенном в переменное синусоидальное
электрическое поле с напряженностью Е
и угловой частотой ω возникают
электрические токи двух видов: ток
смещения Iсм
и ток проводимости Iпр.
Плотность тока смещения

Iсм=j*ω*ε0*ε*E.

плотность тока
проводимости

Iпр=γаЕ.

где
γа-
удельная активная проводимость
диэлектрика на угловой частоте ω.

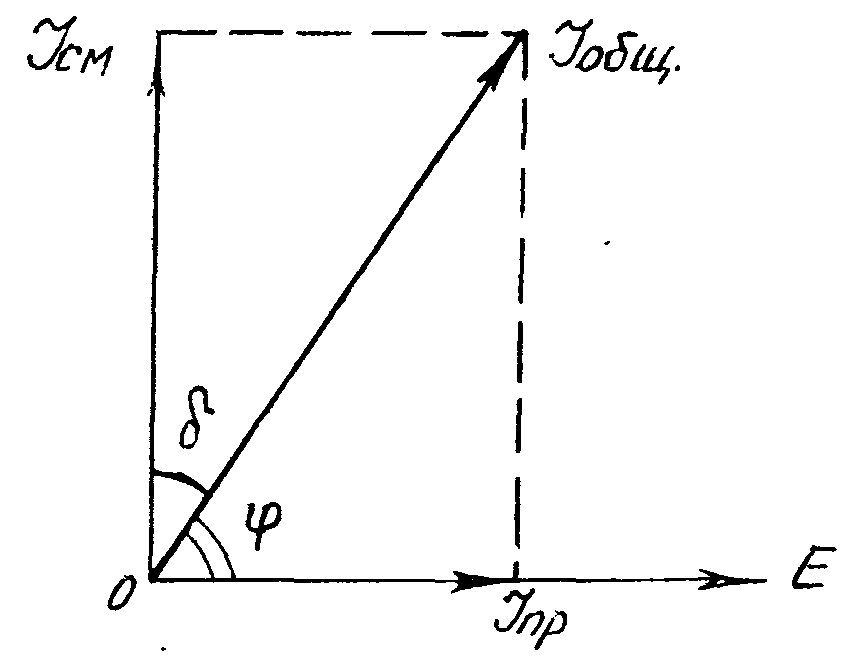
Плотность общего тока равна векторной
сумме плотностей токов смещения и
проводимости (рис.3).

Разрушающее напряжение для материала изготовления при растяжении на изгибе

Рис.3. Векторная диаграмма токов в
диэлектрике

на комплексной
плоскости.

Если
бы диэлектрик был идеальным, т.е. без
потерь (γа
= 0), то был бы чисто реактивным и его
плотность

I
= Icм=
j*ωε0εЕ

была бы направлена по мнимой оси под
углом 90° к вектору Е. Однако, у реальных
диэлектриков с удельной активной
проводимостью на частоте ω отличной
от нуля, суммарный ток сдвинут на угол
δ = 90°-φ относительно тока идеального
диэлектрика (φ-угол сдвига фаз между
током и напряжением).

Чем
больше удельная активная проводимость
диэлектрика, тем больше угол δ,
характеризующий степень отличия
реального диэлектрика от идеального.
Угол δ между векторами плотностей
переменного тока диэлектрика и тока
смещения на комплексной плоскости
называют углом диэлектрических
потерь.
Тангенс этого угла

tgδ
= Inp/Icм
= γa/ωεoε
является одним из важнейших параметров
не только диэлектриков, но, также
конденсаторов, изоляторов и других
электроизоляционных элементов.

Мощность, рассеиваемая
в единице объема вещества, так называемые
удельные диэлектрические потери
определятся как:

P=γa•E2=
ω*ε0*ε*Е2
tgδ (Вт/м3).

Чем
выше tgδ
,тем больше нагрев диэлектрика в
электрическом поле заданной частоты и
напряженности.

Введение
безразмерного параметра tgδ
удобно потому, что он не зависит от формы
и размеров участка изоляции, а определяется
лишь свойствами диэлектрического
материала. Полные диэлектрические
потери в диэлектрике с емкостью С
(активная мощность, теряемая в диэлектрике)
при приложении напряжения U
с угловой частотой ω= 2πf,
где f-частота,
Гц, определится по формуле:

Pa=U2*πf*C*tgδ,

таким
образом, tgδ
определяет потери в диэлектриках.

Наряду
с потерями tgδ характеризует добротность
конденсаторов и, следовательно,
максимальную добротность контура с
данным конденсатором (Q=l/tgδ).

Высокие диэлектрические
потери приводят к разогреву и тепловому
пробою диэлектриков в сильном электрическом
поле, снижению добротности и избирательности
колебательных контуров. В связи с этим
стремятся снизить tgδ диэлектрических
материалов, что возможно, если известны
природа диэлектрических потерь.

Следует различать
механизм диэлектрических потерь на
электропроводность от релаксационных
потерь резонансных и ионизационных.
Тот или иной механизм потери мощности
в диэлектрике зависит как от состава
диэлектрика, так и от параметров внешнего
электрического поля, на него
воздействующего.

В условиях размещения
диэлектрика в электрическом поле не
очень высокой напряженности физические
явления, происходящие в нем при этом,
практически оставляют диэлектрик
непроводящей средой.

Однако силы
электрического поля при соответствующем
увеличении напряженности могут
привести к нарушению такого состояния.
В результате диэлектрик из непроводящего
состояния перейдет в состояние
высокой проводимости в узком канале,
направленном от электрода к электроду.
Явление образования в диэлектрике
проводящего канала под действием
электрического поля называют пробоем.

Минимальное
приложенное к образцу диэлектрика
напряжение, приводящее к его пробою,
называют пробивным напряжением Uпр.
Напряженность однородного поля (поля,
в котором напряженность во всех точках
одинакова) при котором происходит
пробой-разрушение диэлектрика с
образованием в нем сквозного канала с
очень большой проводимостью — называют
электрической прочностью диэлектрика,
которую рассчитывают по формуле:

Enp=
Unp/h
(В/м),

где
Unp-пробивное
напряжение;

h-
толщина диэлектрика в месте пробоя. В
виду того, что диэлектрики пробиваются
при очень больших напряжениях (тысячи
вольт), значение электрической прочности
выражают в мегавольтах на метр толщины
материала в месте пробоя (МВ/м).

Вольт-амперная
характеристика образца диэлектрика
или электрической изоляции линейна при
обычных напряжениях и отклоняется
от линейной с приближением к пробивному
напряжению, а в момент пробоя ток
через диэлектрик резко возрастает, так
что dI/dU→∞(рис.
4).

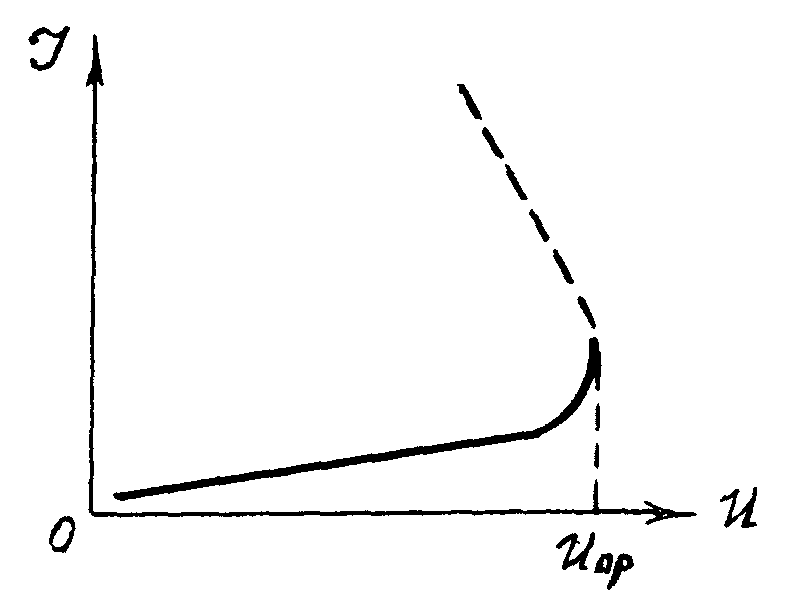Разрушающее напряжение для материала изготовления при растяжении на изгибе Рис.
4. ВАХ образца диэлектрика.

В месте пробоя
возникает искра или электрическая дуга.
Вследствие образования плазменного
сильно проводящего канала между
электродами образец оказывается
короткозамкнутым, и напряжение на
нем падает несмотря на рост тока.

Номинальное
напряжение электрической изоляции
должно быть меньше пробивного напряжения.
Величину, равную отношению пробивного
напряжения к номинальному напряжению,
называют коэффициентом
запаса электрической прочности.

Значение
Unp
диэлектрика непосредственно связано
со временем приложения напряжения.
Так при кратковременных импульсах
пробой происходит при больших
напряжениях, чем в случае постоянного
или длительного приложения переменного
напряжения. Продолжительное воздействие
электрического поля высокой напряженности
приводит к необратимым процессам в
диэлектрике, в результате которых его
пробивное напряжение снижается т.е.
происходит его электрическое старение.
Вследствие такого старения срок службы
изоляции ограничен.

Источник

Полистирол

Разрушающее напряжение при изгибе - таблицы электронного справочника по химии, содержащие Разрушающее напряжение при изгибе

Полистирол

Сырье и марки Производители

производителей полистирола

Полистирольные изделия и продукция Оборудование для получения и переработки полистирола Книги и журналы о полистиролах Фотографии Процесс производства полистирола Исторические факты Перспективы и прогнозы развития

Краткие характеристики и свойства:

Полистирол получают полимеризацией стирола в массе (ПСМ), в эмульсии (ПСЭ) и реже-в суспензии (С). Средняя молекулярная масса (ММ) =80-100тысяч в зависимости от способа получения. Формула полистирола: [CH2-CH-]n | C6H5 Полистирол и материалы на его основе относятся к конструкционным полимерным материалам.

Они характеризуются достаточно высокой прочностью, жесткостью, высокой размерной стабильностью, отличными декоративными свойствами. Полистирол — аморфный полимер, характеризующийся высокой прозрачностью (светопропускание до 90%).

Полистирол (ПС, бакелит, вестирон, стирон, фостарен, эдистер и др.).

Плотность 1,04-1,05 г/см3, tразм 82-95 С. Полистирол растворяется в стироле и ароматических углеводородах, кетонах. Полистирол не растворяется в воде, спиртах, слабых растворах кислот, щелочей. Модуль при изгибе 2700-3200 МПа. Теплопроводность 0,08-0,12 Вт/(м*К). Ударная вязкость по Шарпи с надрезом 1,5-2 кДж/м2.

Полистирол склонен к растрескиванию. Температура самовоспламенения 440 С. КПВ пылевоздушной смеси 25-27,5 г/м3.Полистирол хрупок, стоек к щелочам и ряду кислот, к маслам, легко окрашивается красителями, не теряя прозрачности, имеет высокие диэлектрические свойства.

Полистирол не токсичен, допущен к контакту с пищевыми продуктами и к использованию в медико — биологической технике.

УПС (ударопрочный полистирол) получают привитой сополимеризацией стинола с полибутадиеновыми или бутадиенстирольными каучуками. Ударопрочный полистирол (УП, каринекс, люстерекс, стернит, стирон, хостирен идр.)Структурно УПС представляет собой трехфазную систему, состоящую из ПС (полистирола), гель Фракии привитого сополимера и каучука с привитым стиролом в виде частиц размером до 15 мкм, равномерно распределенным по объему УПС. Несмотря на низкую молекулярную массу матричного полистирола (70-100 тыс.), присутствие каучука существенно замедляет рост микротрещин, что и повышает прочность материала (табл. 1).
В марке УПС указывается метод синтеза (М, С), цифровое обозначение ударной вязкости (две первые цифры) и десятикратное значение содержания остаточного мономера. Кроме того, в марку могут включать букву, обозначающую предпочтительный способ переработки. Например, УПМ-0703 Э — ударопрочный полистирол, полученный полимеризацией в массе; его ударная вязкость 7 кДж/м2 , остаточное содержание мономера 0,3%, переработка — экструзией.

Таблица 1.

Основные свойства полистирольных пластиков

Свойства полистирола	ПС	УПС	АБС	МСН
Плотность, кг/м3	1050	1060	1040	1040
Температура плавления, 0С	190-230	190-230	210-240	205-220
Разрушающее напряжение, МПа, при:
Растяжении	35-40	27-56	36-60	90-100
Изгибе	55-70	55-60	50-87	—
Сжатии	80-100	—	46-80	—
Относительное удлинение при разрыве, %	1,0-1,5	1,0-2,0	1,0-3,0	—
Ударная вязкость, кДж/м2	12-20	40-50	80-100	11-18
Твердость по Бринеллю, МПа	150	110	100	170
Теплостойкость по Мартенсу, 0С	60-70	65	86-98	70-72
Диэлектическая проницаемость при 106 Гц	2,5	2,7	2,4-5,0	2,9
Тангенс угла диэлектрических потерб при 106 Гц, х104	2-4	4-8	300	1,8
Удельное объемное электрическое сопротивление, Ом∙м	1015	5∙1013	5∙1013	4∙1014
Электрическая мощность, МВ/м	25-40	—	12-15	24

АБС — пластик является продуктом привитой сополимеризации трех мономеров — акрилонитрила, бутадиена и стирола, причем статический сополимер стирола и акрилонитрила образует жесткую матрицу, в которой распределены частицы каучука размером до 1 мкм.

Повышение ударной прочности сопровождается сохранением на высоком уровне основных физико-механических и теплофизических свойств (табл. 1). АБС непрозрачен. Выпускается стабилизированным в виде порошка и гранул. Применяется для изготовления изделий технического назначения.

В марке АБС первые две цифры означают величину ударной вязкости по Изоду, следующие две — ПТР (показатель текучести расплава), буква в конце марки указывает на метод переработки или на особые свойства. Например, АБС-0809Т характеризуется ударной вязкость — 8 кДж/м2 , ПТР — 9г/10 мин, повышенной теплостойкостью (Т).

В промышленности используются сополимеры стинола с акрилонитрилом (САН), стинола с метилиетакрилатом (МС) и стинола с метиметакрилатом и акрилонитрилом (МСН).
Полистирол перерабатывается всеми известными способами.

Механические свойства полистирола

Полистирол	Разрушающее напряжение , МПа при:	Е, ГПа
растяжении	изгибе	сжатии
ПС	95	60	70	1,2

Механическая стойкость полистиролов к кислотам и растворителям:

Полистирол	Н2SO4 20-60%	HNO3 50%	HCl до 37%	Ацетон	Этанол	Бензол	Фенол
ПС	3	2	3	1; 2	3	1-3	—
УПС	3	2	3	1; 2	3	1	—
АБС	3	2	3	—	—	—	—

Теплофизические свойства полистиролов:

Полистирол	*Теплопроводность, λ, Вт/(мК)**	*Теплоемкость, с, кДж/(кгК)**	*Температуропроводность, a107, м2/с**	*Средний КЛР (β105),К-1**
ПС	0,09-0,14	1,16-1,3	0,94	6-7
АБС	0,12	1,24	0,9	8-10

Температурные характеристики:

Полистирол	Пределы рабочих температур, С	Температура размягчения по Вика	Теплостойкость по Мартенсу	Температура плавления С
верхний	нижний
ПС	65-70	-40	82-105	76-82	160-175
АБС	75-85	-60	99-100	90-104	165-180

Диэлектрическая проницаемость полистиролов:

Полистиро	έ при v, Гц
50	103	106
ПС	2,65	2,6	2,6

Показатель возгораемости (К) — безразмерная величина, выражающая отношение количества тепла, выделенного при горении к количеству тепла, затраченному на поджигание образца материала. Материал с показателем К>0,5 является горючим. Для полистирола показатель К-1,4 материал является горючим

Показатели пожароопасности полистиролов:

Полистиро	*Температура, С*	*Теплота сгорания*
Тв	*Тсв*	*МДж/кг*
Полистирол ПС	345	490	39-41

Особенности горения полистирола и ударопрочного полистирола:
Поведение пламени: Вспыхивает при поджигании, горит легко. Горит и после удаления из пламени.

Окраска пламени: Оранжево-желтое, светящееся.
Характер горения: Горит с образованием большого количества копоти, плавится.
Запах : Сладковатый цветочный с оттенком запаха бензола.

Запах корицы, если уколоть раскаленной иглой. Сладковатый запах стирола.

Краткое описание, методы переработки, основное назначение, качественная оценка свойств полистиролов и специфические особенности

Полистирол блочный, эмульсионный, суспензионный: Более жесткий материал чем ПЭВД И ПЭНД, с хорошими диэлектрическими свойствами, недостаток хрупкость и низкая теплостойкость. Химическистоек.

Для повышения ударной вязкости и теплостойкости используют сополимеризацию стирола с другими мономерами или совмещение его с каучуками.

При введении в полистирол порофоров м последующем вспенивании получают пенополистирол, отличающийся высоким тепло и звукоизоляционными свойствами, плавучестью, химической стойкостью и водостойкостью

Методы переработки: Литье под давлением. Пневматическое и вакуумное формование. Экструзия. Штамповка. Прессование. Склейка. Механическая обработка

Основное назначение: Для корпустных деталий приборов, ридиоэлектронной аппаратуры, изоляторов, крупногабаритных деталей холодильников, внутренней отделки самолетов. Пенополистрирол для тепло и звукоизоляции в строительстве

Полистрирол ударопрочный: Более высокая ударная вязость чем у полистрирола

Основное назначение: Для технических изделий и деталей

Модифицированный полистирольный пластик: Высокая ударная вязкость при низких и высоких температурах, повышенная нагревостойкость, стойкость к щелочам и смазочным маслам

Методы переработки: Литье под давлением. Экструзия. Раздувка

Основное назначение: Для крупногабаритных изделий в автомобилестроении и в электротехнике

Техническая механика

Как было установлено ранее, в поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия. Вопрос о распределении этих напряжений по поперечному сечению решается путем рассмотрения деформаций волокон балки.

Рассмотрим участок балки, подверженный деформации чистого изгиба. Двумя поперечными сечениями АВ и СD выделим элемент балки бесконечно малой длины ds (рис 1). Радиус кривизны нейтрального слоя балки обозначим ρ.

Рассмотрим слой волокон mn, находящийся на расстоянии y от нейтрального слоя NN. Это волокно в результате деформации изгиба удлинилось на величину nn1. Ввиду малости расстояния ds заштрихованные треугольники будем считать прямолинейными; эти треугольники подобны (n1F || mE):

Δ OEF ~ Δ Fnn1.

Из подобия треугольников запишем равенство:

nn1 / ds = y / ρ.

Так как левая часть этого равенства есть относительное удлинение, т. е. nn1 / ds = ε, то y / ρ = ε.

Применив закон Гука при растяжении и сжатии σ = Еε, получим:

σ = Еy / ρ.

Из этой формулы видно, что нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.
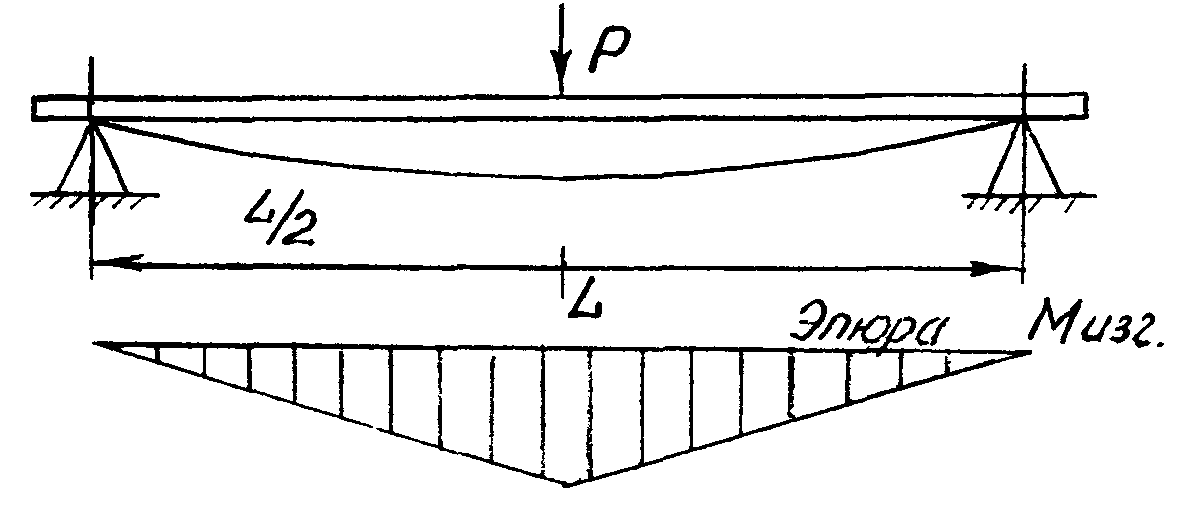
Распределение нормальных напряжений изображено на рис. 2.

Полученная формула для определения нормальных напряжений неудобна, так как в нее входит радиус кривизны нейтрального слоя.

Для вывода формулы, связывающей нормальные напряжения с изгибающим моментом, применим метод сечений и рассмотрим равновесие части балки, изображенной на рис. 3.

В плоскости поперечного сечения выделим бесконечно малую площадку dA, в пределах которой будем считать нормальные напряжения σ постоянными; тогда нормальная сила dN, действующая на площадку dA, будет равна:

dN = σdA.

Составим уравнения равновесия:

1. Σ Z = 0; ∫dN = 0, или: ∫σ dA = ∫Еy / ρ dA = Е / ρ ∫y dA = 0.

(ρ для данного сечения, а также модуль упругости Е – величины постоянные, поэтому вынесены за знак интеграла). Поскольку ρ и Е не равны нулю, значит, ∫y dA = 0.

Этот интеграл представляет собой статический момент площади сечения относительно оси x, т. е. нейтральной оси бруса (балки).

Равенство нулю статического момента инерции означает, что при изгибе нейтральная ось проходит через центр тяжести площади поперечного сечения;

2.Σ Ми = 0; — m + ∫y dN = 0.

Так как при чистом изгибе изгибающий момент равен внешнему моменту Ми = m, то

Ми = ∫y dN = ∫y dA = ∫y Еy / ρ dA = Е / ρ ∫y2 dA,

откуда:

Ми = Е I / ρ,

где: I = ∫y2 dA – момент инерции поперечного сечения относительно нейтральной оси; ЕI – жесткость сечения при изгибе.

Так как при чистом изгибе балки постоянного сечения Ми = const, то:

ρ = EI / Ми = const.

Следовательно, изогнутая ось такой балки представляет собой дугу окружности. Выражение радиуса кривизны подставим в формулу для определения нормальных напряжений; тогда:

σ = Еy / ρ = Ey / EI / Ми = Ми y / I.

Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:

σmax = Ми ymax / I = Ми / I / ymax = Ми / W,

где W = I / ymax – момент сопротивления изгибу (или осевой момент сопротивления). Момент сопротивления изгибу есть отношение осевого момента инерции поперечного сечения относительно нейтральной оси к расстоянию от этой оси до наиболее удаленного волокна.
Единица момента сопротивления сечения изгибу [W] = м3.

Итак, наибольшие нормальные напряжения при чистом изгибе вычисляются по формуле

σmax = Ми / W.

Нетрудно заметить, что эта формула по своей структуре аналогична формулам для определения напряжений при растяжении, сжатии, сдвиге и кручении.

***

Очевидно, что при поперечном изгибе, вызванном приложением к балке поперечной силы, в сечениях балки должны возникнуть касательные напряжения.

Определением зависимости между внешними нагрузками, геометрическими и физическими параметрами балок и касательными напряжениями, возникающими в них, занимался русский мостостроитель Д. И.

Журавский, который в 1855 году предложил следующую формулу:

τ = QS / (I d).

Эта формула называется формулой Журавского и читается так:
касательные напряжения в поперечном сечении балки равны произведению поперечной силы Q на статический момент S относительно центральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину b рассматриваемого слоя волокон.

По формуле Журавского можно вывести зависимости для определения касательных напряжений в балках, имеющих разную форму поперечного сечения (прямоугольную, круглую и т. п.).
Например, для балки круглого сечения формула Журавского в результате преобразований выглядит так:

τmax = 4Q / (3A) = 4τсред / 3,

где Q – поперечная сила, вызывающая изгиб, А – площадь сечения балки. Большинство балок в конструкциях рассчитывается только по нормальным напряжениям, и только три вида балок проверяют по касательным напряжениям: — деревянные балки, т. к.

древесина плохо работает на скалывание; — узкие балки (например, двутавровые), поскольку максимальные касательные напряжения обратно пропорциональны ширине нейтрального слоя; — короткие балки, так как при относительно небольшом изгибающем моменте и нормальных напряжениях у таких балок могут возникать значительные поперечные силы и касательные напряжения.

Максимальное касательное напряжение в двутавровой балке определяется по формуле Журавского, при этом геометрические характеристики таких балок берутся из справочных таблиц .

***

Расчеты на прочность при изгибе

Условие на прочность при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое.

Полагая, что гипотеза о не надавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения при поперечном изгибе определять по такой же формуле, что и при чистом изгибе, при этом расчетная формула выглядит так:

σmax = Миmax / W ≤ [σ]

и читается так: нормальное напряжение в опасном сечении, определенное по формуле σmax = Миmax / W ≤ [σ] не должно превышать допускаемое.

Допускаемое нормальное напряжение при изгибе выбирают таким же, как при растяжении и сжатии. Максимальный изгибающий момент определяют по эпюре изгибающих моментов или расчетом.

Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то чем больше W, тем меньшие напряжения возникают в сечении бруса.

Ниже приведены моменты сопротивления изгибу для наиболее часто встречающихся сечений:

1. Прямоугольное сечение размером b x h: Wпр = bh2 / 6.

2. Круглое сечение диаметром d: Wкруг = π d3 / 32 ≈ 0,1d3

3. Кольцо размером D x d: Wкольца = ≈ 0,1 (D4 – d4) / D; (момент сопротивления кольцевого сечения нельзя определять, как разность моментов сопротивления большого и малого кругов).

***

Материалы раздела «Изгиб»:

Деформации растяжения и сжатия

Олимпиады и тесты

Источник