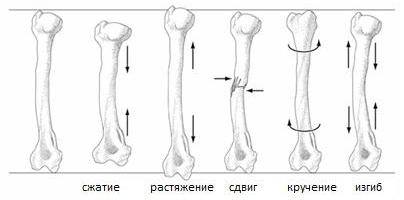
Растяжения сжатия сдвига изгиба кручения

- 大型ファミリープール
- 長方形フレームプール
- イージーセットプール
- 丸形フレームプール
- 大型プールセット
- キッズプール
- 別売品
ホーム > 草刈り機 > 【最大80%オフ】のゼノア刈払機 BKZ315L RYOBI(リョウビ) 背負い式(背引きスタート/STレバー)始動性·低振動だから疲れにくく 末松電子、ナイロンカッターとの相性抜群!《北海道 アルインコ、沖縄、離島は別途、送料がかかります。:代引き不可》【新作モデルセール】の
タイプでえらぶ
- 長方形タイプ
- 丸形タイプ
ゼノア刈払機 BKZ315L 背負い式 ループハンドル
(背引きスタート/STレバー)
New!
低燃費&ハイパワー!低振動だから疲れにくく、ナイロンカッターとの相性抜群!
| ■ストラト?チャージド | 環境に対応したストラト?チャージドエンジンを搭載しています。 | |||
| ■草地向け | 畔刈りや家周り、日々の草刈り等に適しています。 | |||
| ■ナイロンカッタ選択可 | ナイロンカッタも使用できます。 | |||
| ■低振動 | Newダンパシャフトをさらに改良。振動を低減しています。 | |||
| ■緑化管理向け | 公園緑化?ゴルフ場?道路等の施設管理に適しています。 | |||
| ■くるくるカッター | エンジン部がくるくると回転。操作棹が自由自在です。 | |||
| 仕様 | |||
| エンジン仕様 | |||
| 排気量 | 29.5cm3 | ||
| 始動方式 | EZスタート | ||
| スパークプラグ | NGK CMR7H-10 | ||
| キャブレタ | ダイヤフラム式 ロータリーバルブ | ||
| 外形寸法 | |||
| 本体乾燥質量 | 8.4 kg | ||
| 全長(背負部) | 2655mm ※エンジンと桿部を含めた長さです | ||
| 全長(操作桿部) | |||
| 全幅(背負部) | 305mm | ||
| 全高(背負部) | 330mm | ||
●製品を組み立てる前に、必ず説明書に記載された注意事項をよくお読み下さい。
●組み立てが終わり試運転の際には説明書に従って適切に行って下さい。
●商品は2個口での発送になります。
| ※送料について |
| ※送料無料の商品ですが下記地域の場合送料が別途送料が必要となります。 お手数をでしょうがご落札前に必ずお問い合わせ下さい。 【対象地域:北海道?沖縄?離島】 |
| ※送料について |
| ※送料無料の商品ですが下記地域の場合送料が別途送料が必要となります。 お手数をでしょうがご落札前に必ずお問い合わせ下さい。 【対象地域:北海道?沖縄?離島】 |
| ※メーカー直送のため、代引きのご利用が出来ません。 |
カタチでえらぶ
- 全ての商品一覧
ブランドでえらぶ
- 0円~4,999円
- 5,000円~10,000円
- 10,000円~20,000円
- 20,000円~50,000円
- 50,000円~10万円
- 10万円以上
- 商品の梱包サイズ(参考)
- 全国のプール施設一覧
- 大型プールへの思い
- 動作環境について
- 新着投稿
- アンケート
- 【ISEKIアグリ】歩行型草刈機 ハンマーナイフモアー『HRC664』 クローラタイプ[草刈機 草刈り機 刈払機 共立 オーレック ヰセキ イセキ]
- クリテック カクハンキ(撹拌機) 長さ:4m SK-4L 両回転仕様 【L型ジョイント付】
- 12/04-11 POINT最大44倍/【送料無料】セフティ-3 背負半自動噴霧器 10型 17L 散水 殺虫 消毒 園芸 観賞植物 農薬散布 除草 4977292860895
- 76464e0edu-jpw7nraolo03csdiiarrhdthp0pduse.jp
大型ビニールプールのお店
ビザンコマースプールでは、大人も楽しめる大きいビニールプールを通信販売しています。 激安販売、子供用ビニールプールを家庭用に販売 intex社製、ベストウェイ社製を中心に 家庭用大型ビニールプールを取扱、長方形 楕円形 丸型 滑り台など自宅の 屋上 ベランダで子供 ペットが安全に遊べます トイザラスには売っていません
家庭用大型ビニールプール専門店|ビザンコマース poolお奨めの商品!
商品価格は全て税込
です、合計金額11,000円以上は送料無料
- 共立エコー エンジン式刈払機 EGT261DL
です!faxによるご注文も受け付けております!
家庭用大型ビニールプール専門店|ビザンコマース poolからのお知らせ!
| 『お父さん・お母さんへ』 |
| ご家族で、お友達と、仕事先・趣味仲間達と皆で一緒に大きなプールに入りませんか? 土地の広いアメリカにはご家庭のお庭に大きなプールを夏ごとに設置して、 仲間たちとバーベキューなどしながら楽しんでいます。 照りつける真夏の太陽!ちょっと冷水をひと浴び!なんてことがご家庭でいつでも出来るようになります。 【最大80%オフ】のゼノア刈払機 BKZ315L RYOBI(リョウビ) 背負い式(背引きスタート/STレバー)始動性·低振動だから疲れにくく 末松電子、ナイロンカッターとの相性抜群!《北海道 アルインコ、沖縄、離島は別途、送料がかかります。:代引き不可》【新作モデルセール】のまた夜に月を見ながらプールに浮かんでビールを飲む!なんてことも・・・
夏休みの家族皆のとっておきの海岸はいつでも行ける庭先にありました!! |
| 『おじいちゃん・おばあちゃんへ』 |
| お孫さん家族が帰っていらっしゃるときにぜひご用意ください。 なかなか若い夫婦は庭付きのおうちには住めません、ぜひ実家のお庭に大きなプールを! きっとお孫さんの特別な夏休みになるはずですよ!来年は今年よりもっと早く帰ってくるかも! |
| 『愛犬の夏バテ防止に』 |
| もうそろそろ熱くなってきました。愛犬は大丈夫ですか?暑さにやられていませんか? 水を掛けてやるだけでもずいぶんと涼しくなると思いますが、 思い切ってプールで泳がしてあげてはいかがでしょう?もともとワンちゃんは水泳が大得意! 大きなプールで泳がせてあげれば大喜び間違いなしです! 犬介護用プールとしても・・・ |
| 『園長先生・施設理事長様へ』 |
| 子供達や施設の方々にとっておきの夏のプレゼントをされませんか? 子供達の喜ぶ顔が目に浮かびます。 夏バテ防止、疲労回復にもなるのできっと素敵なプレゼントになると思います。 サイズも色々取り揃えておりますので、様々な場所に設置可能です。 また小さく折りたためるものが多数ありますので翌シーズンまで締まって置けます。 |
| 『研究施設・工場長様へ』 |
| ある程度の水深を必要とする実験等を行う場合に、大型簡易仮設プールは安価に環境を構築できる優れものです。 大きな試験物を使う場合には外部に委託するよりも安価に評価ができます。 各施設より多くのご注文を頂いております。薬品等をご利用の場合は耐性をあらかじめご確認をお願いいたします。 |
| 『スポーツ部監督・部長様へ』 |
| 温室効果の影響もあり、夏場の日光の強さが特に厳しくなっております。選手たちの熱中症対策として、大型プールは多くのチームで活用されています。グランド等の日陰にプールを設置して起き、クールダウンの時にメンバーたちで漬かることで素早く体温管理ができます。是非ご検討ください。 |
| 『魚業関係者様へ』 |
【最大80%オフ】のゼノア刈払機 BKZ315L RYOBI(リョウビ) 背負い式(背引きスタート/STレバー)始動性·低振動だから疲れにくく 末松電子、ナイロンカッターとの相性抜群!《北海道 アルインコ、沖縄、離島は別途、送料がかかります。:代引き不可》【新作モデルセール】の
魚のつかみ取りイベントや、簡易水槽として安価にご利用いただけます。大きさも様々なサイズを取り揃えておりますのでどうぞご活用ください。 |
Источник
Растяжение (сжатие). К стержню (бруску) длиной l и площадью поперечного сечения Sприкладывается сила F, направленная перпендикулярно сечению (рис. 11.1). В результате этого в теле возникает механическое напряжениео, которое в данном случае характеризуется отношением силы к площади поперечного сечения стержня (малое изменение площади поперечного сечения не учитывается):

В СИ механическое напряжение измеряется в паскалях (Па).

Рис.2.1. Деформации растяжения и сжатия
Под действием приложенной силы длина стержня изменяется на некоторую величину ?l, которая называется абсолютной деформацией. Величина абсолютной деформации зависит от первоначальной длины стержня, поэтому степень деформации выражают через отношение абсолютной деформации к первоначальной длине. Это отношение называется относительной деформацией (е):

Относительная деформация — величина безразмерная. Иногда
ее выражают в процентах:

При небольшой величине относительной деформации связь между деформацией и механическим напряжением выражается законом Гука:
гдеЕ— модуль Юнга, Па (модуль продольной упругости).
При упругой деформациинапряжение прямо пропорционально величине деформации.
Модуль Юнга численно равен напряжению, увеличивающему длину образца в два раза (практически разрушение образцов наступает при значительно меньших напряжениях). В табл. 11.1 представлены значения модулей упругости некоторых материалов.
В большинстве случаев при растяжении или сжатии степень деформации в различных сечениях стержня различна. Это можно увидеть, если на поверхность тела нанести квадратную сетку. После деформирования сетка исказится. По характеру и величине этого искажения можно судить о распределении напряжения вдоль образца (рис. 11.2).
Таблица 11.1
Модуль упругости (модуль Юнга) некоторых материалов
Материал | Модуль Юнга E, Па |
Эластин | 105-106 |
Коллаген | 107-108 |
Мембрана эритроцита | 4?107 |
Клетки гладких мышц | 104 |
Мышца в покое | 9?105 |
Кость | 2?109 |
Сухожилие | 1,6?108 |
Нерв | 18,5-106 |
Вена | 8,5?105 |
Артерия | 5?104 |
Древесина | 12?109 |
Резина | 5?106 |
Сталь | 2?1011 |
Видно, что изменения формы ячеек сетки максимальны в средней части стержня и почти отсутствуют на его краях.
Сдвиг. Деформация сдвига возникает, если на тело действует касательная сила, приложенная параллельно закрепленному основанию (рис. 11.3). В этом случае направление смещения свободного основания параллельно приложенной силе и перпендикулярно боковой грани. В результате деформации сдвига прямоугольный параллелепипед превращается в косоугольный. При этом боковые грани смещаются на некоторый угол г, называемый углом сдвига.

Рис. 2.2.Искажениеквадратнойсетки при растяжении стержня
Рис. 2.3. Деформация сдвига
Абсолютная деформация сдвига измеряется величиной смещения свободного основания (?l). Относительная деформация сдвига определяется через тангенс угла сдвига tgг, называемый относительным сдвигом. Так как угол у обычно мал, то можно считать
При сдвиге в образце возникает напряжение сдвига ф (касательное напряжение), которое равно отношению силы (F) к площади основания (S),параллельно которому действует сила:


При небольшой величине относительной деформации сдвига связь между деформацией и механическим напряжением выражается эмпирическим соотношением:
где G— модуль сдвига, Па.
Изгиб. Этот вид деформации характеризуется искривлением оси или срединной поверхности деформируемого объекта (балка, стержень) под действием внешних сил (рис. 11.4). При изгибе один наружный слой стержня сжимается, а другой наружный слой растягивается. Средний слой (называемый нейтральным) изменяет лишь свою форму, сохраняя длину. Степень деформирования бруска, имеющего две точки опоры, определяется по перемещению X, которое получает середина стержня. Величина А, называется стрелой прогиба.

Рис. 2.4. Деформации изгиба
Применительно к прямому брусу в зависимости от направления действующих сил изгиб называют продольным или поперечным. Продольный изгиб возникает под действием сил, направленных вдоль бруса и приложенных к его концам навстречу друг другу (рис. 11.5, а). Поперечный изгиб возникает под действием сил, направленных перпендикулярно, брусу и приложенных как к его концам, так и в средней части (рис. 11.5, б). Встречается также и смешанный продольно-поперечный изгиб (рис. 11.5, в).

Рис. 2.5. Различные виды изгиба: а) продольный, б) поперечный, в) продольно-поперечный
Кручение. Этот вид деформации характеризуется взаимным поворотом поперечных сечений стержня под влиянием моментов (пар сил), действующих в плоскости этих сечений. Кручение возникает, например, когда нижнее основание стержня закреплено, а верхнее основание поворачивают вокруг продольной оси, рис. 11.6.
При этом расстояние между различными слоями остается практически неизменным, но точки слоев, лежащих на одной вертикали, сдвинуты относительно друг друга. Этот сдвиг в разных местах будет различен. Например, в центре сдвига совсем не будет, по краям он будет максимальный. Таким образом, деформация кручения сводится к деформации сдвига, различному в разных частях, т. е. к неоднородному сдвигу.

Основание фиксировано
Рис. 2.6. Деформации кручения

Рис. 2.6,а. Устранение асимметрии лица с помощью лейкопластыря
Абсолютная деформация при кручении характеризуется углом поворота (ц) одного основания относительно другого. Относительная деформация (и) равна отношению угла ц к длине стержня:

Сравнивания различные способы деформирования однородных тел, можно увидеть, что все они сводятся к комбинации растяжения (сжатия) и сдвига.
Пример
Для устранения асимметрии лица после травмы проводится лейкопластырное натяжение со здоровой стороны на больную, рис. 11.6, а.
Лейкопластырное натяжение направлено против тяги мышц здоровой кожи и осуществляется прочной фиксацией другого свободного конца пластыря к специальному шлему — маске, изготовленному индивидуально.
Источник
Деформация сдвига, кручения, изгиба – это изменение объема и формы тела при воздействии на него дополнительной нагрузки. При этом меняются расстояния между молекулами или атомами, приводящие к появлению сил упругости. Рассмотрим основные виды деформаций и их характеристики.

Сжатие и растяжение
Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.
Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.
Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.
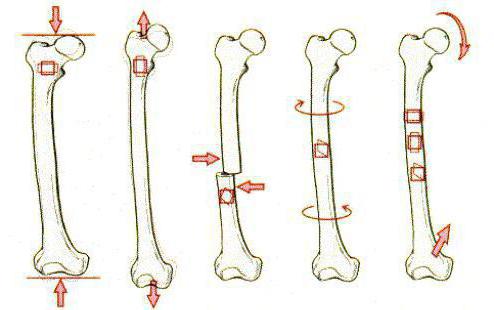
Деформация изгиба
Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.
В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.
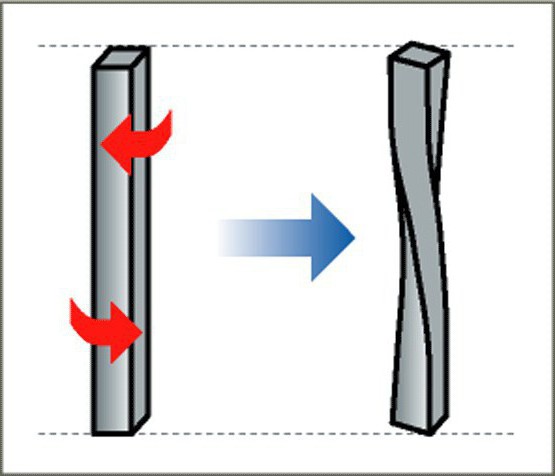
Деформация кручения
Эта продольная деформация является неоднородным сдвигом. Она возникает при действии сил, направленных параллельно либо противоположно на стержень, у которого закреплен один конец. Чаще всего сложным деформациям подвергаются различные детали и механизмы, применяемые в конструкциях и машинах. Но благодаря сочетанию нескольких вариантов деформаций, существенно облегчается вычисление их свойств.
Кстати, в процессе существенной эволюции кости птиц и животных приняли трубчатый вариант строения. Такое изменение способствовало максимальному упрочнению скелета при определенной массе тела.
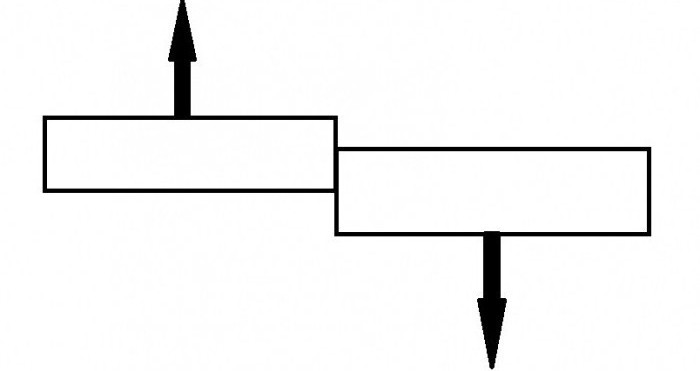
Деформации на примере организма человека
Тело человека подвергается серьезным механическим нагрузкам от собственных усилий и веса, появляющихся по мере физической деятельности. Вообще, деформация (сдвиг) характерна для человеческого организма:
- Сжатие испытывает позвоночник, покровы ступней, нижние конечности.
- Растяжению подвергаются связки, верхние конечности, мышцы, сухожилья.
- Изгиб характерен для конечностей, костей таза, позвонков.
- Кручениям подвергается во время поворота шея, при вращении ее испытывают кисти рук.
Но при превышении показателей предельного напряжения, возможен разрыв, например костей плеча, бедра. В связках же ткани соединяются настолько эластично, что допускается растягивание их в два раза. Кстати, деформация сдвига объясняет всю опасность передвижения женщин на высоких каблуках. Вес тела будет переноситься на пальцы, что приведет к повышению нагрузки на кости в два раза.
По результатам медицинских осмотров, проводимых в школах, из десяти детей лишь одного можно считать здоровым. Как деформации связаны с детским здоровьем? Сдвиг, кручение, сжатие – основные причины нарушения осанки у детей и подростков.
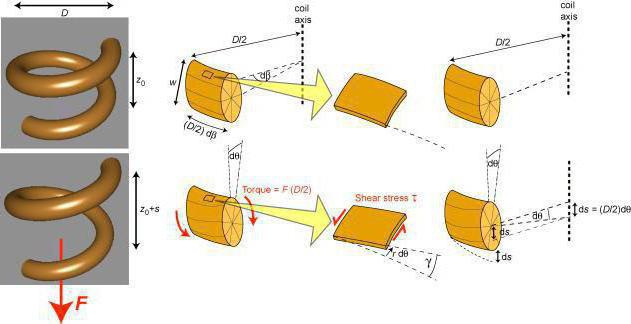
Прочность и деформации
Несмотря на многообразие живого и неживого мира, на создание человеком многочисленных материальных объектов, у всех предметов и живых существ есть общее свойство — прочность. Под ней принято понимать способность материала сохраняться на протяжении длительного временного промежутка без видимых разрушений. Существует прочность конструкций, молекул, сооружений. Эта характеристика уместна для кровеносных сосудов, человеческих костей, кирпичной колонны, стекла, воды. Деформация сдвига – вариант проверки сооружения на прочность.
Применение разных видов деформаций человеком имеет глубокие исторические корни. Все начиналось с желания соединить между собой палку и острый наконечник, чтобы охотиться на древних животных. Уже в те далекие времена человека интересовала деформация. Сдвиг, сжатие, растяжение, изгиб помогали ему создавать жилища, орудия труда, готовить пищу. По мере развития техники человечеству удалось использовать различные виды деформаций так, чтобы они приносили весомую пользу.
Закон Гука
Математические расчеты, необходимые в строительстве, технике, позволили применять закон Гука для деформации сдвига. Формула показывала прямую связь между силой, прикладываемой к телу, и его удлинением (сжатием). Гук использовал коэффициент жесткости, показывая связь между материалом и возможностью его деформации.
По мере развития и совершенствования технических средств, аппаратов и приборов, разработки теории сопротивления, были проведены серьезные исследования пластичности и упругости. Результаты проведенных фундаментальных экспериментов стали применять в строительной технике, теории сооружений, теоретической механике.
Благодаря комплексному подходу к проблемам, связанным с различными видами деформации, удалось развить строительную отрасль, осуществлять профилактику правильной осанки у подрастающего поколения страны.
Заключение
Деформации, рассматриваемые в курсе школьной физики, оказывают влияние на процессы, происходящие в живом мире. В организмах человека, животных постоянно происходит кручение, изгиб, растяжение, сжатие. И для того чтобы осуществлять своевременную и полноценную профилактику проблем, связанных с осанкой или избыточным весом, медики используют зависимости, выявленные физиками при проведении фундаментальных исследований.
Например, прежде чем осуществлять протезирование нижних конечностей, выполняется детальный расчет максимальной нагрузки, на которую он должен быть рассчитан. Протезы подбираются для каждого человека индивидуально, так как важно учесть вес, рост и подвижность последнего. При нарушениях осанки применяют специальные коррекционные пояса, основанные на использовании деформации сдвига. Современная реабилитационная медицина не смогла бы существовать без использования физических законов и явлений, в том числе и без учета закономерностей различных видов деформаций.
Источник
В машиностроении, строительстве и архитектуре при расчетах прочности и жесткости материалов используется математический аппарат технической механики. Деформация растяжения – одно из ключевых понятий, характеризующее механические процессы, происходящие в материалах при приложении к ним внешних воздействий. Для наглядности изучаются изменения, происходящие в брусе с постоянным сечением, характерные для упругой деформации при приложении внешних усилий.
Закон Гука (английский физик Р. Гук, 1653-1703) для упругой деформации растяжения/сжатия гласит, что нормальное напряжение находится в линейной зависимости (прямо пропорционально) к относительному удлинению/укорочению. Математический аппарат технической механики описывает эту формулу следующим образом:
Коэффициент пропорциональности E (модуль упругости, модуль Юнга) – величина определяющая жесткость материала, единица измерения – паскаль (ПА).
Его значения были установлены эмпирическим путем для большинства конструкционных материалов, необходимую информацию можно почерпнуть в справочниках по машиностроению. Относительная деформация является отношением изменения длины бруса к его изначальным размерам, это безразмерная величина, которая иногда отражается в процентном соотношении.
При растяжении или сжатии у бруса меняется не только длина, но происходят поперечные деформации: при сжатии образуется утолщение, при растяжении толщина сечения становится меньше. Величины этих изменений находятся в линейной зависимости друг от друга, причем установлено, что коэффициент пропорциональности Пуассона (фр. ученый С. Пуассон, 1781-1840) остается всегда неизменным для исследуемого материала.
Внутренние усилия при растяжении и сжатии
При приложении к брусу с постоянным сечением внешних воздействий, действие которых в любом поперечном разрезе направлено параллельно его центральной оси и перпендикулярно сечению, с ним происходит следующий вид деформации: растяжение или сжатие. На основе гипотезы о принципе независимости внешнего воздействия для каждого из поперечных разрезов можно рассчитать внутреннее усилие как векторную сумму всех приложенных внешних воздействий. Растягивающие нагрузки в сопромате принято считать положительными, а сжимающие отрицательными.
Рассмотрев произвольный разрез бруса или стержня, можно сказать что внутренние напряжения равны векторной сумме всех внешних сил, сгруппированных по одной из его сторон. Это верно только с учетом принципа Сен-Венана (фр. инженер А. Сен-Венан, 1797-1886) о смягчении граничных условий, т.к. распределение внутренних усилий по поверхности разреза носит сложный характер с нелинейными зависимостями, но в данном случае значением погрешности можно пренебречь как несущественным.
Применяя гипотезу Бернулли (швейцарский математик, И. Бернулли, 1667-1748) о плоских сечениях, для более наглядного представления процессов распределения сил и напряжений по центральной оси бруса можно построить эпюры. Визуальное представление более информативно и в некоторых случаях позволяет получить необходимые величины без сложных расчетов. Графическое представление отражает наиболее нагруженные участки стержня, инженер может сразу определить проблемные места и ограничиться расчетами только для критических точек.
Все вышесказанное может быть применимо при квазистатической (система может быть описана статически) нагрузке стержня с постоянным диаметром. Потенциальная энергия системы на примере растяжения стержня определяется по формуле:
U=W=FΔl/2=N²l/(2EA)
Потенциальная энергия растяжения U концентрируется в образце и может быть приравнена к выполнению работы W (незначительное выделение тепловой энергии можно отнести к погрешности), которая была произведена силой F для увеличения длины стержня на значение абсолютного удлинения. Преобразуя формулу, получаем, что вычислить значение величины потенциальной энергии растяжения можно, рассчитав отношение квадрата продольной силы N помноженной на длину стержня l и удвоенного произведения модуля Юнга E материала на величину сечения A.
Как видно из формулы, энергия растяжения всегда носит положительное значение, для нее невозможно применить гипотезу о независимости действия сил, т.к. это не векторная величина. Единица измерения – джоуль (Дж). В нижней части формулы стоит произведение EA – это так называемая жесткость сечения, при неизменном модуле Юнга она растет только за счет увеличения площади. Величина отношения жесткости к длине бруса рассматривается как жесткость бруса целиком.
Напряжения при растяжении сжатии
Используя гипотезу Бернулли для продольной упругой деформации стержня, можно определить продольную силу N как равнодействующую всех рассредоточенных по сечению внутренних усилий. Гипотеза Бернулли совместно с гипотезой о ненадавливании волокон позволяет сказать, что σ в произвольной точке разреза будут постоянны, т.к. реакция продольных волокон одинакова на всем поперечном разрезе. Для определения величины нормального напряжения σ используется следующая формула:
Напряжение для упруго деформированного стержня описывается как отношение внутренней силы N к площади сечения A. Считается положительным при растяжении, при сжатии рассматривается как отрицательное.
Абсолютная деформация зависит от жесткости сечения, величины продольной силы и длины бруса. Зависимость можно описать по следующей формуле:
Δl=Nl/EA
Таким образом, методика расчета величины абсолютного изменения длины такова: необходимо просчитать отношение значения продольной силы N умноженной на длину стержня l и жесткости сечения (произведение модуля Юнга E на площадь сечения A).
В реальных расчетах на брус действует достаточно много разнонаправленных сил, для решения таких задач требуется построение эпюр, которые могут наглядно показать какие напряжения действуют на разных участках, чем обусловлена деформация при растяжении и сжатии.
В рамках такой квазистатической (условно статической) системы, как брус или стержень с переменным сечением или отверстием, потенциальная энергия растяжения может быть рассмотрена как сумма энергий однородных участков. При проведении расчетов важно правильно разделить стержень на участки и смоделировать все участвующие в процессе силы и напряжения. Для реальных расчетов построение эпюр – сложная задача, которая требует от инженера хорошего понимания действующих на деталь нагрузок. Например, вал со шкивами разного диаметра требует сначала определения критических точек и разбивки на соответствующие участки, затем построения графиков по ним.
Деформации при растяжении сжатии
При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.
Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.
Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.
Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:
F=kx
В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.
Расчеты на прочность и жесткость
Прочность характеризует способность конструкционного материала сопротивляться внешним воздействиям без разрушений и остаточных изменений. Жесткость находится в линейной зависимости от модуля Юнга и размера сечения. Чем больше площадь, модуль упругости не меняется, тем больше жесткость. В общем случае жесткость подразумевает способность деформироваться без значительных изменений. Коэффициент запаса прочности – безразмерная величина, равная отношению предельного напряжения к допустимому. Запас прочности характеризует штатный режим работы конструкции даже с учетом случайных и не предусмотренных нагрузок. Наименьшим запасом прочности обладают пластические (1.2-2.5) и хрупкие (2-5) материалы.
Применение в расчетах этих коэффициентов позволяет, например, рассчитать опасную толщину для стержня, при которой может возникнуть максимальное нормальное напряжение. Используя коэффициент прочности и возможное предельное напряжение возможно произвести расчет необходимого диаметра вала, который гарантированно обеспечит упругую деформацию и не приведет к пластической. Для инженеров-экономистов важны расчеты наименьших безопасных размеров деталей конструкции по заданным нагрузкам.
Большинство практических расчетов на прочность и жесткость производятся для получения минимальных значений геометрических размеров конструкционных элементов и деталей машин в условиях известных внешних воздействий и необходимого и достаточного запаса прочности. Может решаться обратная задача получения значений предельных нагрузок при условии сохранения геометрических размеров и для конкретного материала.
Сложные конструкции могут быть разделены на элементарные части, для которых будут производиться расчеты, затем полученные результаты интерпретируются в рамках всей системы, для этого удобно строить эпюры распределения внешних воздействий и внутренних напряжений статически определенной системы.
С помощью известной жесткости материала делают расчеты максимально возможной длины балки или стержня (вала) при условии неизменности его сечения. Для ступенчатых валов необходимо строить эпюры воздействия внешних сил и возникающих в точках их приложения внутренних напряжений в критических точках. От правильно построенной теоретической модели будет зависеть насколько эффективно и долго прослужит вал для станка, не разрушится ли он от динамических крутящих моментов. На этапе проектирования можно выявить потенциальные слабые точки и рассчитать необходимые параметры для заданного предела прочности.
С расчетами на прочность связаны такие понятия, как срез и смятие. Срез проявляется в виде разрушения детали соединения в условиях возникновения в ее поперечном сечении перпендикулярной к нему и достаточной силы.
При расчетах соединений используют пределы текучести используемых материалов и коэффициенты запаса прочности, вычисляют максимально возможные напряжения.
Исследования на прочность обычно подразумевают решение нескольких задач: в условиях проведения поверочного расчета на проверку прочности при известных усилиях и площади сечения оценивают фактический коэффициент запаса прочности; подбор оптимального диаметра при заданных нагрузках и допустимом напряжении; вычисляют грузоподъемность или несущую способность с помощью определения внутреннего усилия при известной площади сечения и напряжении.
Прочностные расчеты при разных видах воздействий в рамках условно статических систем сложны, требуют учета многих, иногда не очевидных, факторов, их практическая ценность заключается в вычислении допустимых размеров конструкционных материалов для заданных параметров запаса прочности.
Источник
