Растяжением и сжатием называют такой вид нагружения

Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Виды нагружения бруса, при котором в его поперечном сечении возникает только один внутренний силовой фактор – , называемый растяжением или сжатием.
Как вычисляется значение продольной силы в произвольном поперечном сечении стержня?
Значение продольной силы в произвольном поперечном сечении стержня вычисляется по формуле N = ∑F
Что такое эпюра продольных сил и как она строится?
Эпюра продольных сил — это график показывающий изменение величины продольных сил сечение бруса по его длине.
Чтобы построить эпюру нужно знать следующий алгоритм построения:
1. Разбиваем брус на участке ограниченными точками приложения сил (разбивка на участке ведётся с незакреплённого участка бруса).
2. Используя метод сечений определяют величину продольных сил сечения каждого участка (резать с незакреплённого участка).
3. Строим эпюру продольных сил, выбрав соответствующий масштаб.
Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого или центрально-сжатого стержня, и по какой формуле они определяются?
Нормальных напряжений S = const. Тогда N = S· F , откуда получим формулу для определения нормальных напряжений в поперечном сечении при растяжении
Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций?
Если же по длине стержня возникает неоднородное напряженное состояние, то для определения его абсолютного удлинения необходимо рассмотреть бесконечно малый элемент длиной dz. При растяжении он увеличит свою длину на величину D dz и его деформация составит: .
относительной продольной деформацией называют деформацией относительно деформируемого предмета
Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?
8.
Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела упруго деформироваться при приложении к нему силы.
В области упругой деформации модуль упругости тела определяется производной (градиентом) зависимости напряжения от деформации, то есть тангенсом угла наклона диаграммы напряжений-деформаций.
Коэффициент пропорциональности E — модуль продольной упругости, его величина постоянна для каждого материала. Он характеризует жесткость материала, т.е. способность сопротивляться деформированию под действием внешней нагрузки..
Сформулируйте закон Гука. Напишите формулы для абсолютной и относительной продольных деформаций стержня.
В пределах малых удлинений для большинства материалов справедлив закон Гука — нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформации .
Формулы для абсолютной и относительной продольных деформаций стержня: ; ;
Что происходит с поперечными размерами стержня при его растяжении (сжатии)?
Наблюдения показывают, что его удлинение в продольном направлении сопровождается пропорциональным уменьшением поперечных размеров стержня.
Что такое коэффициент Пуассона? В каких пределах он изменяется?
Коэффициент Пуассона (обозначается как или ) — абсолютная величина отношения поперечной и продольной относительной деформации образца материала. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала.
При приложении к телу растягивающего усилия оно начинает удлиняться (то есть продольная длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз поперечная деформация деформируемого тела больше продольной деформации, при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно несжимаемого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5.
Источник

РАСТЯЖЕНИЕ И СЖАТИЕ Под растяжением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы, а все прочие внутренние силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
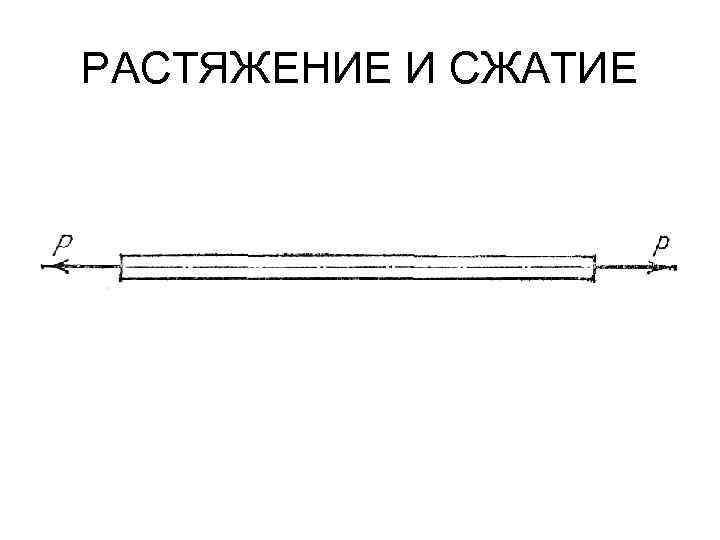
РАСТЯЖЕНИЕ И СЖАТИЕ

РАСТЯЖЕНИЕ И СЖАТИЕ Естественно предположить, что для однородного стержня внутренние силы распределены по сечению равномерно. Тогда нормальное напряжение для всех точек сечения будет одним и тем же: σ=N/F где F — площадь поперечного сечения.

РАСТЯЖЕНИЕ И СЖАТИЕ Понятно, что высказанное предположение справедливо лишь постольку, поскольку из рассмотрения исключаются особенности конкретно взятого стержня в связи с условиями его закрепления на концах.

РАСТЯЖЕНИЕ И СЖАТИЕ Для этого руководствуются принципом Сен-Венана: особенности приложения внешних сил к растянутому стержню проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня.

РАСТЯЖЕНИЕ И СЖАТИЕ Для нагруженного по концам растянутого однородного стержня напряжения остаются постоянными как по сечению, так и по длине. Такое напряженное состояние называется однородным. При однородном напряженном состоянии все точки тела находятся в одинаковых условиях.

РАСТЯЖЕНИЕ И СЖАТИЕ При растяжении, однако, не всегда возникает однородное напряженное состояние. Так, например, у стержня с переменной площадью поперечного сечения напряжения меняются по длине и напряженное состояние не однородно. То же самое имеет место и для стержня, нагруженного собственным весом.
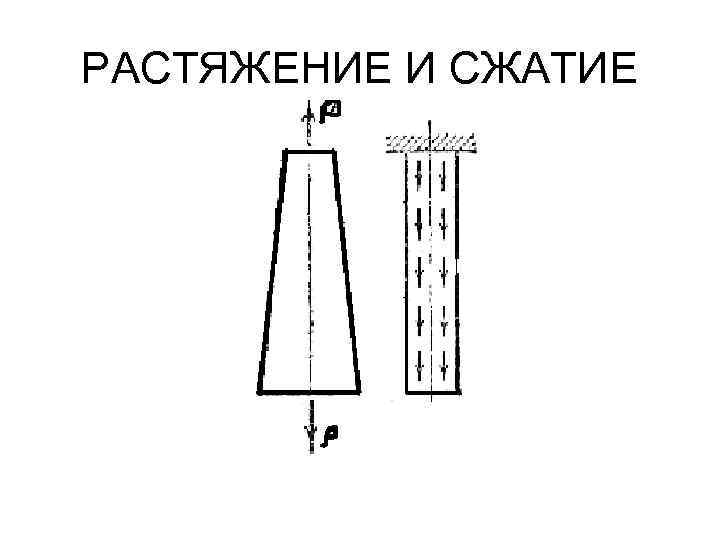
РАСТЯЖЕНИЕ И СЖАТИЕ

Удлинения стержня и закон Гука Размеры растянутого стержня меняются в зависимости от величины приложенных сил. Если до нагружения стержня его длина была равна L, то после нагружения она станет равной L +Δ L. Величину Δ L называют абсолютным удлинением стержня.
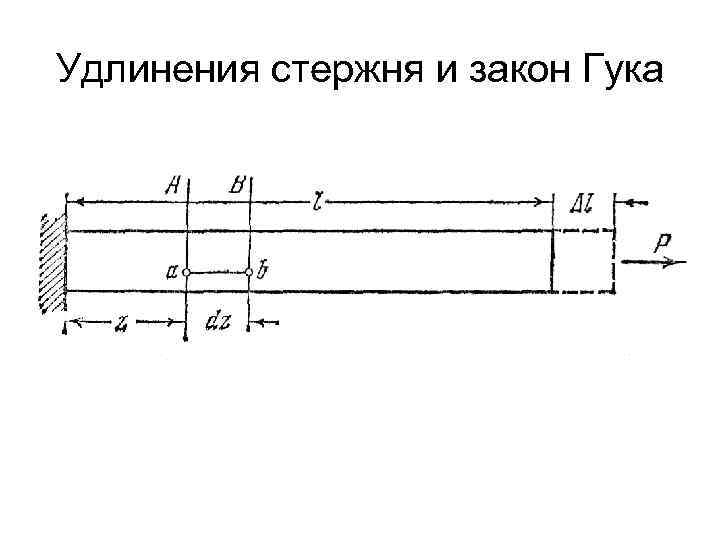
Удлинения стержня и закон Гука

Удлинения стержня и закон Гука Абсолютное удлинение и деформации связаны только с напряжениями, возникающими в стержне. В действительности имеются и другие факторы, влияющие на деформации зависят от температуры и от времени действия нагрузки. Неупругие деформации зависят от «истории» нагружения, т. е. от порядка возрастания и убывания внешних сил.

Удлинения стержня и закон Гука Поскольку у нагруженного стержня напряженное состояние является однородным и все участки растянутого стержня находятся в одинаковых условиях, деформации ε по оси стержня остается одной и той же, равной своему среднему значению по длине L: ε= Δ L / L Эта величина начинается относительным удлинением стержня.

Удлинения стержня и закон Гука Если бы в стержне возникало неоднородное напряженное состояние, деформация в сечении А определялась бы путем предельного перехода к малому участку длиной dz, и тогда ε=Δ(dz)/ dz

Удлинения стержня и закон Гука Вследствие равномерного распределения напряжений можно утверждать, что если концы отрезков до нагружения образуют плоскость, то и после нагружения стержня они образуют плоскость, но смещенную вдоль оси стержня. Это положение может быть взято в основу толкования механизма растяжения и сжатия и трактуется как гипотеза плоских сечений (гипотеза Бернулли).

Удлинения стержня и закон Гука В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями: =Е ε (1). Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода.

Удлинения стержня и закон Гука Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и , т. е. в мегапаскалях.

Удлинения стержня и закон Гука Вернемся к выражению (1) и заменим в нем на N/F, а ε на ∆(dz)/dz. Тогда получим ∆(dz)=N dz/EF Абсолютное удлинение стержня на длине L будет равно ∆L= 0∫L N dz/EF (2)

Удлинения стержня и закон Гука В том случае, когда стержень нагружен только по концам, нормальная сила N=P не зависит от z. Если, кроме того, стержень имеет постоянные размеры поперечного сечения F, то получаем ∆L=P L /E F

Потенциальная энергия деформации Внешние силы, приложенные к упругому телу, совершают работу. Обозначим ее через А. В результате этой работы накапливается потенциальная энергия деформированного тела U. Кроме того, работа идет на сообщение скорости массе тела, т. е. преобразуется в кинетическую энергию К. Баланс энергий имеет вид A = U+K.

Потенциальная энергия деформации Если нагружение производится медленно, скорость будет весьма малой. Такой процесс нагружения называется статическим. Тело в любой момент времени находится в состоянии равновесия. В этом случае A=U, и работа внешних сил целиком преобразуется в потенциальную энергию деформации.

Потенциальная энергия деформации При разгрузке тела за счет потенциальной энергии производится работа. Таким образом, упругое тело является аккумулятором энергии. Это свойство упругих тел широко используется, например, в различных упругих амортизирующих элементах рессоры, пружины, торсионные валы.

Потенциальная энергия деформации Определим работу А и соответственно потенциальную энергию растянутого стержня. Поскольку на пути ∆L сила Р не остается постоянной, работа, затраченная на растяжение стержня, должна быть определена интегрированием по элементарным участкам пути.

Потенциальная энергия деформации На элементарном перемещении d(∆L ) работа текущей силы Р равна d. A=Pd(∆ L ). Очевидно, работа на перемещении ∆ L численно равна площади треугольника ОВС, т. е. A = U=1/2 Р ∆ L.
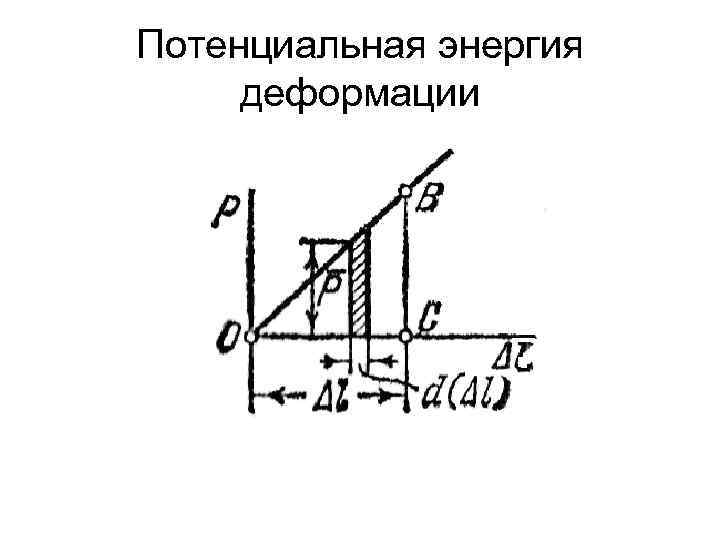
Потенциальная энергия деформации

Потенциальная энергия деформации Подставив в полученное для U выражение значение ∆L , найдем U = Р 2 L / 2 Е F

Потенциальная энергия деформации Если нормальная сила N меняется вдоль оси стержня, то потенциальная энергия деформации должна определяться суммированием по участкам dz. Для элементарного участка d. U=N 2 dz/2 Е F а для всего стержня U= o∫L N 2 dz/2 Е F
Источник
