Растяжение срез смятие кручение изгиб

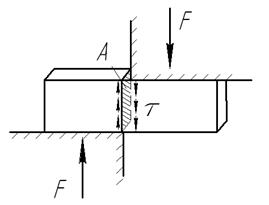 Срезом называют деформацию, представляющую собой смещение поперечных плоскостей тела под действием силы параллельной этой плоскости.
Срезом называют деформацию, представляющую собой смещение поперечных плоскостей тела под действием силы параллельной этой плоскости.
Касательные напряжения при срезе (напряжения среза) определяются по формуле
где — действительные напряжения среза;
— допускаемые напряжения растяжения (сжатия);
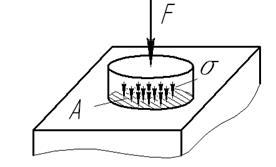 Смятием называют деформацию, представляющую собой нарушение первоначальной формы поверхности под действием силы перпендикулярной к этой поверхности.
Смятием называют деформацию, представляющую собой нарушение первоначальной формы поверхности под действием силы перпендикулярной к этой поверхности.
Нормальные напряжения при смятии (напряжения смятия) определяются по формуле
Пример
Определить напряжения среза и смятия для заклепки соединяющей три детали. Известны диаметр заклепки , усилие действующее на соединение
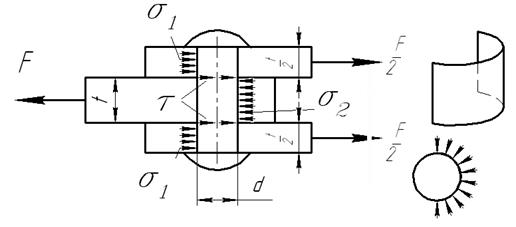
Запишем условие прочности на срез для заклепки
В соединении 3-х деталей напряжения среза возникают в двух сечениях круглой формы.
Площадь круга , подставляем ее в условие прочности, получим.
Запишем условие прочности на смятие для заклепки
В соединении 3-х деталей напряжения смятия возникают на боковых поверхностях заклепки площадь которых будет определяться:
Для верхней и нижней поверхностей:
Для средней поверхности:
Тогда напряжения смятия
Для верхней и нижней поверхностей:
Для средней поверхности:
Изгиб
Изгиб представляет собой такую деформацию, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса.
Изгиб называют чистым если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении бруса (балки).
Изгиб называют поперечным, если в поперечных сечениях бруса наряду с изгибающими моментами возникают также и поперечные силы.
При изгибе в сечении деталей возникают нормальные напряжения , которые распределяются по закону треугольника, причем в нижних волокнах – напряжения сжатия, а в верхних – напряжения растяжения (для схемы показанной на рисунке).
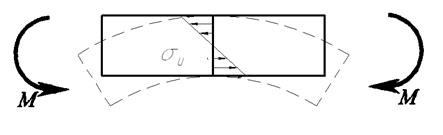
Напряжения изгиба определяются по формуле
На практике изгиб тела вызывает не только внешние изгибающие моменты, но и поперечные силы, действующие на тело. Для нахождения наиболее нагруженного поперечного сечения строят эпюры изгибающих моментов.
При построении эпюр изгибающих моментов используются следующие правила:
1 Тело разбивается на участки, границами которых служат точки приложения внешних сил и моментов и реакции опор;
2 Построение ведется последовательно, по участкам, путем проведения сечений, проходящих через середину участка и отбрасывания части тела лежащей за сечением. Для неотброшенной части тела составляется зависимость по которой изменяется изгибающий момент и определяется его значение в начале и конце участка;
4 Построение эпюры ведется о стороны растянутых волокон;
5 Если в рассматриваемом сечении приложен внешний момент, то на эпюре наблюдается скачек на величину этого момента.
Построение эпюр изгибающих моментов рассмотрим на примере.
Пример
Проверить на прочность балку постоянного сечения, показанную на рисунке, если известно, что осевой момент сопротивления ее сечения м3, а допускаемые напряжения изгиба МПа.
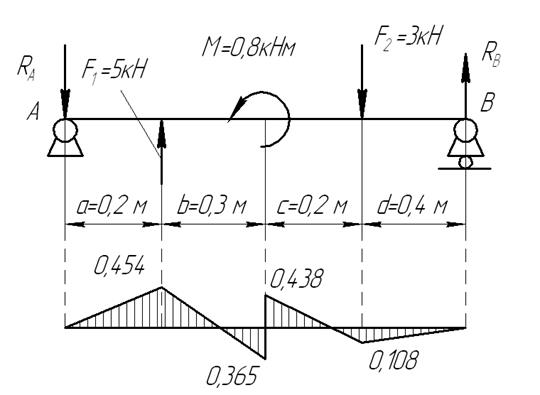
1 Определяем реакции опор
:
кН
:
кН
Проверка
2 Разбиваем эпюру на участки
Участок 1
Участок 2
Участок 3
Участок 4
Проверка
Наибольший момент Н·м
Определяем напряжения изгиба
Кручение
Кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси. Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.
При кручении в сечении деталей возникают касательные напряжения , которые направлены по касательной к окружности вала
Напряжения кручения определяются по формуле
Если вал нагружен несколькими крутящими моментами, то для нахождения наиболее нагруженного поперечного сечения строят эпюры крутящих моментов.
При построении эпюр крутящих моментов принимают следующее правило знаков: если при взгляде в торец отсеченной части вала действующий в этом сечении момент оказывается направленным против хода часовой стрелки, то он считается положительным, а если по ходу часовой стрелки — отрицательным.
Пример
На валу установлено 4 диска, к которым подвешены грузы.
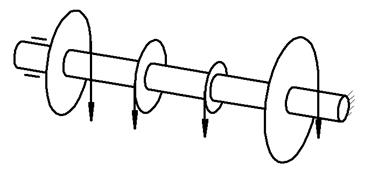
Проверить на прочность вал показанный на рисунке. Известен диаметр вала d = 75 мм, диаметры дисков d1 = 200 мм, d2 = 150 мм, d3 = 100 мм, d4 = 250 мм и вес грузов F1 = 20кН, F1 = 40кН, F1 = 35кН, F1 = 40 кН допускаемое напряжение не кручение = 25 МПа
Определим крутящие моменты на валах
кН·м
кН·м
кН·м
кН·м
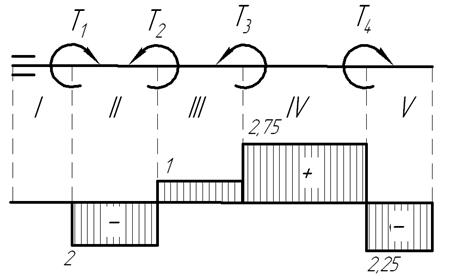
Строим расчетную схему и эпюру крутящих моментов
Разбиваем вал на участки
Рассматриваем участок I: Проводим сечение I-I и отсекаем правую часть
Рассматриваем участок II: Проводим сечение II-II и отсекаем правую часть
кН·м
Рассматриваем участок III: Проводим сечение III-III и отсекаем правую часть
кН·м
Рассматриваем участок IV: Проводим сечение IV — IV и отсекаем правую часть
кН·м
Рассматриваем участок V: Проводим сечение V — V и отсекаем правую часть
кН·м
По эпюре определяем наибольший момент кН·м
Записываем условие прочности
Источник
Сдвигом называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — поперечная сила.
Рассмотрим брус, на который действуют две силы, равные по величине (рис. 20) и противоположно направленные. Эти силы перпендикулярны к оси бруса, и расстояние между ними ничтожно мало. При достаточной величине этих сил происходит срез.
Левая часть тела отделяется от правой по некоторому сечению АВ. Деформация, предшествующая срезу, которая заключается в перекашивании прямых углов элементарного параллелепипеда, называется сдвигом. На рис. 20, б показан сдвиг, происходящий в параллелепипеде до среза; прямоугольник abed превращается в параллелограмм abed‘. Величина ССК, на которую сечение cd сдвинулось относительно соседнего сечения ab, называется абсолютным сдвигом. Угол У, на который изменяются прямые углы параллелепипеда, называется относительным сдвигом.
Рис. 20. Схема деформации сдвига: а) перерезывающие силы, действующие на брус; б) деформация элемента бруса abed
Ввиду малости деформаций угол У можно определить следующим образом:
Очевидно, что в сечении АВ из шести внутренних силовых факторов будет возникать только поперечная сила Q, равная силе F:
Данная поперечная сила Q вызывает появление только касательных напряжений т.
Подобная картина наблюдается в деталях, служащих для соединения отдельных элементов машин, — заклепках, штифтах, болтах и т. п., так как они во многих случаях воспринимают нагрузки, перпендикулярные их продольной оси.
Поперечная нагрузка в указанных деталях возникает, в частности, при растяжении (сжатии) соединяемых элементов. На рис. 21 приведены примеры штифтового (а), заклепочного (б), болтового (в) и шпоночного (г) соединений. Такой же характер нагружения соединительных деталей имеет место и при передаче вращающего момента, например в соединении шестерни с валом с помощью штифта, который при передаче момент от шестерни к валу (или наоборот) несет нагрузку, перпендикулярную его оси.
Рис. 21. Схемы соединений:
а) штифтового; б) заклепочного; в) болтового; г) шпоночного
Действительные условия работы рассматриваемых деталей сложны и во многом зависят от технологии изготовления отдельных элементов конструкции и ее сборки.
Практические расчеты этих деталей носят весьма условный характер и базируются на следующих основных допущениях:
- 1. В поперечном сечении возникает только один внутренний силовой фактор — поперечная сила Q.
- 2. Касательные напряжения, возникающие в поперечном сечении, распределены по его площади равномерно.
- 3. В случае, если соединение осуществлено несколькими одинаковыми деталями (болтами и т. п.), принимается, что все они нагружены одинаково.
Разрушение соединительных элементов (в случае недостаточной прочности) происходит в результате их перерезывания по плоскости, совпадающей с поверхностью соприкосновения соединяемых деталей (см. рис. 21,6). Поэтому говорят, что эти элементы работают на срез, и возникающие в их поперечном сечении касательные напряжения также называют напряжениями среза и обозначают тср.
На основе сформулированных выше допущений получаем следующее условие прочности на срез:
где гСр — расчетное напряжение среза, возникающее в поперечном сечении рассчитываемой детали; Q — поперечная сила, вызывающая срез соединительных элементов (болтов, заклепок и т. п.); [тср] — допускаемое напряжение на срез, зависящее от материала соединительных элементов и условий работы конструкции; ZAcp — суммарная площадь среза: LAcp — Асрт (здесь Аср — площадь среза одного соединительного элемента; z — число соединительных элементов; / — количество плоскостей среза в одном соединительном элементе).
В машиностроении при расчете штифтов, болтов, шпонок и т. д. принимают [тср] = (0,5…0,6)*[о] — для пластичных материалов и [хср] = (0,8… 1,0)-[а] — для хрупких материалов. Меньшие значения принимают при невысокой точности определения действующих нагрузок и возможности не строго статического нагружения.
Формула (30) является зависимостью для проверочного расчета соединения на срез. В зависимости от постановки задачи она может быть преобразована для определения допускаемой нагрузки или требуемой площади сечения (проектный расчет).
Расчет на срез обеспечивает прочность соединительных элементов, но не гарантирует надежности конструкции (узла) в целом. Если толщина соединяемых элементов недостаточна, то давления, возникающие между стенками их отверстий и соединительными деталями, получаются недопустимо большими. В результате стенки отверстий обминаются и соединение становится ненадежным. В случае, если изменение формы отверстия значительно (при больших давлениях), а расстояние от его центра до края элемента невелико, часть элемента может срезаться (выколоться).
При этом давления, возникающие между поверхностями отверстий и соединительных деталей (рис. 22, а)у принято называть напряжениями смятия и обозначать их Ос*. Соответственно расчет, обеспечивающий выбор таких размеров деталей, при которых не будет значительных деформаций стенок отверстий, называют расчетом на смятие. Распределение напряжений смятия на поверхности контакта деталей весьма неопределенно (рис. 22, б) ив значительной степени зависит от зазора (в нена- груженном состоянии) между стенками отверстия и болтом (заклепкой и др.).
Рис. 22. Передача давлений на стержень заклепки: а) общий вид заклепочного соединения; б) распределение напряжений по образующей; в) площадь смятия заклепки
Расчет на смятие также носит условный характер и ведется в предположении, что силы взаимодействия между деталями равномерно распределены по поверхности контакта и во всех точках нормальны к этой поверхности.
Соответствующая расчетная формула имеет вид
где F — нагрузка, вызывающая смятие; 1АСМ — суммарная площадь смятия; [С„] — допускаемое напряжение на смятие, устанавливаемое опытным путем. В расчетах принимают: [асм = (2,..2,5)-[[ас] — допускаемое напряжение на сжатие того из контактирующих материалов, прочность которого меньше.
За расчетную площадь смятия при контакте по плоскости (рис. 21, г) принимают действительную площадь соприкосновения Асм = 1-1, где / — размер шпонки в направлении, перпендикулярном плоскости чертежа; при контакте по цилиндрической поверхности (см. рис. 21, а, б, в и рис. 22, а, в) за расчетную площадь принимают площадь проекции поверхности контакта на диаметральную плоскость, т. е. Асм = d-d. При различной толщине соединяемых деталей в расчетную формулу следует подставлять d„i„. Суммарная площадь смятия ?АСМ = ACM-z (где z — число соединительных элементов).
Как уже говорили, в некоторых конструкциях соединительные детали (штифты, шпонки) работают на срез по продольным сечениям (см. рис. 21, г); предпосылки расчета и его методика остаются такими же, как и при срезе по поперечным сечениям.
Помимо расчетов на срез и смятие необходима проверка прочности соединяемых элементов на растяжение по ослабленному сечению. При этом площадь поперечного сечения принимается с учетом ослаблений:
где А„етто — площадь ослабленного сечения.
На рис. 23 показано болтовое соединение. Силы F стремятся сдвинуть листы относительно друг друга. Этому препятствует болт, на который со стороны каждого листа передаются распределенные по контактной поверхности силы, равнодействующие которых равны F. Эти силы стремятся срезать болт по плоскости раздела листов т — л, так как в этом сечении действует максимальная поперечная сила Q = F.
Считая, что касательные напряжения распределены равномерно, получаем
Рис. 23. Болтовое соединение: а) общий вид; б) площадь смятия
Таким образом, условие прочности болта на срез принимает вид
Отсюда можно найти диаметр болта:
При расчете данного болтового соединения следует учитывать, что нагрузки, приложенные к элементам соединений, помимо среза вызывают смятие контактирующих поверхностей.
где Аа, — представляет собой площадь проекции поверхности контакта на диаметральную плоскость (см. рис. 22, б, в): Аш = 3 d.
Тогда условие прочности на смятие болтового соединения (см. рис. 23)
откуда получаем
Чтобы были удовлетворены условия прочности на срез и на смятие, из двух найденных диаметров следует взять больший, округлив его до стандартного значения.
На срез принято рассчитывать и некоторые сварные соединения (рис. 24).
Рис. 24. Схема сварного соединения: а) расчетная схема углового шва; б) площадь среза ABCD сварного шва
Если не учитывать наплывы, то в разрезе угловой шов имеет форму равнобедренного прямоугольного треугольника (см. рис. 24, а). Разрушение шва будет происходить по его минимальному сечению ABCD (см. рис. 24, б), высота которого к = 3- cos 45° =0,73 .
Для нахлесточного сварного соединения в расчет вводят оба шва. Запишем в этом случае условие прочности шва:
где /т- расчетная длина торцевого шва; т,- допускаемое напряжение для сварных соединений.
Поскольку в начале и в конце шва из-за непровара качество его ухудшается, действительную его длину увеличивают по сравнению с расчетной на 10 мм:
где / — действительная длина шва (на рис. 24, 6:1 = Ь).
Детали, работающие на сдвиг (срез) и смятие
1. Ось (рис. 25, а). В случае, если толщина детали 2 меньше, Ат = Sd;
где / — количество плоскостей (площадей) среза.
2. Болт (рис. 25, б). В этом случае Аср -ndh
Рис. 25. Соединения деталей: а) осью; б) болтом
3. Заклепка односрезная (рис. 26, а двухсрезная (рис. 26, б).
Рис. 26. Расчетная схема заклепочного соединения: а) с одной плоскостью среза; б) с двумя плоскостями среза
- 4. Шпонки (рис. 27, а) работают на срез и смятие, но рассчитываются, в основном, только на смятие. Площади среза и смятия определяются по формулам Аср= Ья1 ACM=lt.
- 5. Сварное соединение (рис. 27, б).
Угловой шов разрушается под углом 45° к плоскости разъема в результате среза: к — катет углового шва, подбирается по толщине свариваемого листа.
Двусторонний шов: Аср=2-0уЪсЬ = 1,4 к Ь.
Рис. 27. Соединения: а) шпоночное; б) сварное
Пример 6. Определить требуемое число заклепок в соединении двух листов, нагруженных силами F = 85 кН (рис. 28). Диаметр заклепок d = 16 мм. Допускаемые напряжения [гср] = 100 МПа, [си] = 240 МПа.
Решение
Из условия прочности на срез
где АСр=к d 2 / 4 — площадь среза; z — количество заклепок.
Тогда
Рис. 28. К примеру расчета заклепочного соединения
Из условия прочности на смятие
где Асм = dS- площадь смятия; z — количество заклепок, получаем
Вывод: для того чтобы не произошло ни среза, ни смятия заклепок, следует установить пять заклепок.
Пример 7. Стальной болт (рис. 29) нагружен силой F= 120 кН. Определить его диаметр d и высоту головки И, если допускаемые напряжения [ор] = 120 МПа, [zcp = бОМПа.
Решение
Определим диаметр болта из условия прочности на растяжение:
откуда
С некоторым округлением принимаем d= 36 мм.
Головка болта может срезаться по цилиндрической поверхности, условно отмеченной на рис. 29 волнистыми линиями. Площадь этой поверхности Аср= ndh.
Рис. 29. Пример расчета болтового соединения
Условие прочности на срез
откуда
Округляя, окончательно принимаем h = 18 мм.
Пример 8. Проверить, удовлетворяют ли условию прочности лобовые швы двух стальных полос, сваренных внахлестку (рис. 30) и находящихся под нагрузкой F- 120 кН. Допускаемое напряжение [гэ] = 80 МПа. Ширина полос Ь- 150 мм и толщина их
Решение
Соединение может разрушиться от разрыва лобовых швов по вертикальным катетам сс’ или от среза этих швов по горизонтальным катетам сс». Однако практика показывает, что шов разрушается по биссекторному сечению, высота которого
где к — катет шва, в нашем случае к = 8.
Такой шов рассчитывают условно на срез по биссекторному сечению из условия прочности:
где Аср = 0,7 ЗЬ — площадь среза одного сварного шва.
Рис. 30. Пример расчета сварного соединения
Вывод: швы недогружены.
Пример 9. Вал передает крутящий момент, равный 27 кН м при помощи шлицевого соединения (рис. 31). Диаметр вала D = 80 мм, внутренний диаметр d = 68 мм, высота шлица h = 6 мм, ширина шлица b — 12 мм, длина соединения / = 100 мм. Число шлицев 2 = 6. Определить напряжения среза и смятия шлица.
Рис. 31. Расчет шлицевого соединения
Решение
Полагая, что все шлицы нагружены одинаково, найдем усилие, приходящееся на один шлиц:
Определим напряжение среза:
Определим напряжение смятия:
Источник
Ðàñòÿæåíèå è ñæàòèå
Ðàñòÿæåíèå è ñæàòèå ìîæíî ñ÷èòàòü ïðîñòåéøèìè âèäàìè íàãðóæåíèÿ ýëåìåíòîâ. Òàêîìó âèäó íàãðóæåíèÿ ïîäâåðãàþòñÿ: ïîëêè ëîíæåðîíîâ è ñòåíîê, ïîäêîñû, òÿãè ñèñòåìû óïðàâëåíèÿ, òðîñîâàÿ ïðîâîäêà.
Ðàññ÷èòàòü ýëåìåíò êîíñòðóêöèè íà ïðî÷íîñòü ïðè ðàñòÿæåíèè (èëè ñæàòèè) — ýòî çíà÷èò, èñõîäÿ èç äåéñòâóþùèõ óñèëèé (ñ ó÷åòîì êîýôôèöèåíòà áåçîïàñíîñòè), îïðåäåëèòü ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ, ïðè êîòîðîì áóäåò âûïîëíÿòüñÿ óñëîâèå
ãäå -íàïðÿæåíèå, âîçíèêàþùåå â ìàòåðèàëå ýëåìåíòà ïðè åãî íàãðóæåíèè.
Ïðè ïðîåêòèðîâî÷íûõ ðàñ÷åòàõ ïîòðåáíàÿ ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ðàññìàòðèâàåìîãî ýëåìåíòà îïðåäåëÿåòñÿ ïî ôîðìóëå
ãäå Ð — ìàêñèìàëüíî âîçìîæíàÿ ñèëà, äåéñòâóþùàÿ âäîëü îñè ýëåìåíòà.
Ïðè ïðîâåðî÷íûõ ðàñ÷åòàõ óäîáíåå ïîëüçîâàòüñÿ ôîðìóëîé
Ïðè íàëè÷èè â ýëåìåíòå êîíñòðóêöèè, ðàáîòàþùåé íà ðàñòÿæåíèå, êîíöåíòðàòîðîâ íàïðÿæåíèÿ â âèäå ðåçêèõ ïåðåõîäîâ ïðîôèëÿ, îòâåðñòèé, íàäðåçîâ, âåëè÷èíó , âçÿòóþ èç òàáë. 3.2-3.6, íåîáõîäèìî óìåíüøèòü íà 5% äëÿ ëåãèðîâàííûõ ñòàëåé è íà 10… 15%-äëÿ àëþìèíèåâûõ ñïëàâîâ è äðóãèõ êîíñòðóêöèîííûõ ìàòåðèàëîâ.
Ñìÿòèå
Ñìÿòèå ìàòåðèàëà ìîæåò ïðîèñõîäèòü â ìåñòàõ ñî÷ëåíåíèÿ îòäåëüíûõ ýëåìåíòîâ êîíñòðóêöèè. Ðàñ÷åò íà ñìÿòèå íåîáõîäèìî ïðîâîäèòü êàê äëÿ ðàçúåìíûõ, òàê è íåðàçúåìíûõ ñîåäèíåíèé; ñòûêîâî÷íûõ óçëîâ, çàêëåïî÷íûõ ñîåäèíåíèé, ñî÷ëåíåíèé òÿã óïðàâëåíèÿ.
Íàïðÿæåíèå ñìÿòèÿ îïðåäåëÿåòñÿ äåëåíèåì ñèëû íà ïëîùàäü êîíòàêòà, à äëÿ îòâåðñòèé — íà ïðîåêöèþ ýòîé ïëîùàäè:
Âåëè÷èíà äîïóñòèìûõ íàïðÿæåíèé ñìÿòèÿ çàâèñèò îò ìàòåðèàëà è âèäà ñîåäèíåíèÿ. Äëÿ íåðàçúåìíûõ çàêëåïî÷íûõ ñîåäèíåíèé èç äåôîðìèðóåìûõ àëþìèíèåâûõ ñïëàâîâ ìîæíî ïðèíÿòü =6000 êãñ/ñì2. Äëÿ óçëîâ, âûïîëíåííûõ èç ñòàëè, îáû÷íî ïðèíèìàþò:
=1,3* -â ñëó÷àå íåïîäâèæíûõ ñîåäèíåíèé;
=0,65* -â ñëó÷àå ìàëîïîäâèæíûõ ñîåäèíåíèé;
=0,2* -â ñëó÷àå ïîäâèæíûõ ñîåäèíåíèé.
Äëÿ ðàñ÷åòà äèàìåòðà áîëòîâ, ðàáîòàþùèõ â äåòàëÿõ èç äðåâåñèíû, ïðåäëàãàåòñÿ ïîëüçîâàòüñÿ ãðàôèêàìè, ïðåäñòàâëåííûìè íà ðèñ. 3.3, à-ïðè äâóñòîðîííåé íàãðóçêå è ðèñ. 3. 3, á-ïðè îäíîñòîðîííåé íàãðóçêå.
Ðèñ 3.3 Ê ðàñ÷åòó äèàìåòðà áîëòîâ
à — ïðè äâóõñòîðîííåé íàãðóçêå, á — ïðè îäíîñòîðîííåé íàãðóçêå
Äëÿ ñîñíû ïåðïåíäèêóëÿðíî âîëîêíàì ìîæíî ïðèíèìàòü =60 êãñ/ñì2.
Ñäâèã
Ïðèìåðîì ñäâèãà, ÷àñòî âñòðå÷àþùèìñÿ íà ïðàêòèêå, ÿâëÿåòñÿ ñðåç áîëòîâ è çàêëåïîê. Ðàññ÷èòàòü äåòàëü íà ñäâèã, ýòî çíà÷èò âûáðàòü òàêîå ñå÷åíèå ïðåäïîëàãàåìîãî ñðåçà, ïðè êîòîðîì áóäåò âûïîëíåíî óñëîâèå
.
Âåëè÷èíà íàïðÿæåíèÿ ñäâèãà îïðåäåëÿåòñÿ ïî ôîðìóëå
, (3. 4)
ãäå Q-ïîïåðå÷íàÿ ñèëà, a F-ïëîùàäü ïðåäïîëàãàåìîãî ñðåçà.
Äëÿ äåôîðìèðóåìûõ àëþìèíèåâûõ ñïëàâîâ è ëåãèðîâàííûõ ñòàëåé ìîæíî ïðèíèìàòü
,
äëÿ óãëåðîäèñòûõ ñòàëåé-0,65… 0,70, äëÿ ìàãíèåâûõ ñïëàâîâ íå áîëåå 0,60 îò ñîîòâåòñòâóþùåãî çíà÷åíèÿ .
Ïðè ïðîåêòèðîâî÷íûõ ðàñ÷åòàõ óäîáíåå ïîëüçîâàòüñÿ ôîðìóëîé
.
(3. 5)
Êðó÷åíèå
Ìíîãèå ýëåìåíòû êîíñòðóêöèè, ïîìèìî ðàñòÿæåíèÿ, ñæàòèÿ è èçãèáà, ìîãóò èñïûòûâàòü íàïðÿæåíèÿ êðó÷åíèÿ. Êðó÷åíèå èìååò ìåñòî âñåãäà, êîãäà ê äåòàëè ïðèëîæåí êðóòÿùèé ìîìåíò, ëèáî êîãäà âåêòîð ïðèëîæåííîé ñèëû íå ñîâïàäàåò ñ îñüþ æåñòêîñòè äàííîãî ýëåìåíòà.
Ìàêñèìàëüíîå íàïðÿæåíèå êðó÷åíèÿ (ñäâèãà) îïðåäåëÿåòñÿ ïî ôîðìóëå
ãäå Ìêð-êðóòÿùèé ìîìåíò, a Wp-ïîëÿðíûé ìîìåíò ñîïðîòèâëåíèÿ ðàññìàòðèâàåìîãî ñå÷åíèÿ.
Èíîãäà âîçíèêàåò íåîáõîäèìîñòü îïðåäåëåíèÿ óãëà çàêðó÷èâàíèÿ ýëåìåíòà . Ýòîò óãîë äëÿ ïðîôèëåé ïîñòîÿííîãî ñå÷åíèÿ ìîæíî îïðåäåëèòü ïî ôîðìóëå
ãäå l-äëèíà ñêðó÷èâàåìîãî ó÷àñòêà; G-ìîäóëü óïðóãîñòè ïðè ñäâèãå è êðó÷åíèè; Jp — ïîëÿðíûé ìîìåíò èíåðöèè ñå÷åíèÿ.
Êðó÷åíèþ ìîãóò ïîäâåðãàòüñÿ íå òîëüêî îòäåëüíûå ýëåìåíòû, íî è ÷àñòè êîíñòðóêöèè, íàïðèìåð êðûëî èëè ôþçåëÿæ,  ýòîì ñëó÷àå êðóòÿùèé ìîìåíò âîñïðèíèìàåòñÿ, êàê ïðàâèëî, çàìêíóòûì êîíòóðîì îáøèâêè. Íàïðÿæåíèÿ êðó÷åíèÿ îïðåäåëÿþòñÿ ïî ôîðìóëå
ãäå F-ïëîùàäü çàìêíóòîãî êîíòóðà; -òîëùèíà îáøèâêè.
Èç ôîðìóëû (3. 8) âèäíî, ÷òî ìàêñèìàëüíûå íàïðÿæåíèÿ áóäóò â òîì ìåñòå çàìêíóòîãî êîíòóðà, ãäå òîëùèíà îáøèâêè ìèíèìàëüíàÿ.
Îòêðûòûå (íåçàìêíóòûå) êîíòóðû êðóòÿùèé ìîìåíò âîñïðèíèìàþò î÷åíü ïëîõî, â ñâÿçè ñ ÷åì ïðè ïðîåêòèðîâàíèè ÷àñòåé è ýëåìåíòîâ êîíñòðóêöèè ÑËÀ æåëàòåëüíî èçáåãàòü èõ ïðèìåíåíèÿ.
Èçãèá
Ïî÷òè âñå ñèëîâûå ýëåìåíòû êîíñòðóêöèè ÑËÀ ïîäâåðãàþòñÿ èçãèáó, ïîýòîìó îò âåëè÷èíû èçãèáàþùèõ ìîìåíòîâ, äåéñòâóþùèõ íà ýëåìåíòû êîíñòðóêöèè, è îò ñïîñîáà èõ âîñïðèÿòèÿ âî ìíîãîì çàâèñèò ìàññà ÷àñòåé è âñåãî ÑËÀ.
Ïðè äåéñòâèè èçãèáàþùåãî ìîìåíòà ïðîèñõîäèò äåôîðìàöèÿ ýëåìåíòà, âñëåäñòâèå ÷åãî â ìàòåðèàëå âîçíèêàþò íàïðÿæåíèÿ. Âåëè÷èíà ýòèõ íàïðÿæåíèé (ðèñ. 3.4) ìåíÿåòñÿ â çàâèñèìîñòè îò óäàëåíèÿ ìàòåðèàëà îò îñè ñå÷åíèÿ.
Ðèñ 3.4 Ðàñïðåäåëåíèå íàïðÿæåíèé â âîëîêíàõ ïðè èçãèáå
Íîðìàëüíûå íàïðÿæåíèÿ â ïðåäåëàõ ïðîïîðöèîíàëüíîñòè îïðåäåëÿþòñÿ ïî ôîðìóëå
ãäå Ì — ìîìåíò ïîïåðå÷íûõ ñèë îòíîñèòåëüíî ðàññìàòðèâàåìîãî ó÷àñòêà; Jx-îñåâîé ìîìåíò èíåðöèè ïëîùàäè ñå÷åíèÿ îòíîñèòåëüíî îñè x; ó — ðàññòîÿíèå îò îñè õ äî òî÷êè, â êîòîðîé îïðåäåëÿåòñÿ íàïðÿæåíèå.
Êàê âèäíî èç ðèñ. 3. 4, íàèáîëüøèì ïî âåëè÷èíå íàïðÿæåíèå îêàçûâàåòñÿ â êðàéíèõ âîëîêíàõ. Ýòî íàïðÿæåíèå îïðåäåëÿåòñÿ ïî ôîðìóëå
ãäå Wx — îñåâîé ìîìåíò ñîïðîòèâëåíèÿ ñå÷åíèÿ.
Îñåâîé ìîìåíò èíåðöèè Jx è îñåâîé ìîìåíò ñîïðîòèâëåíèÿ Wx ñå÷åíèé íàèáîëåå ðàñïðîñòðàíåííûõ ïðîôèëåé (ðèñ. 3. 2)
Ðèñ 3.2 Ñå÷åíèÿ íàèáîëåå ðàñïðîñòðàíåííûõ ïðîôèëåé
ìîæíî âû÷èñëÿòü, èñïîëüçóÿ ôîðìóëû. Ïðèâåäåííûå â òàáë. 3. 7.
Òàáëèöà 3.7 Ìîìåíòû ñîïðîòèâëåíèé è ìîìåíòû èíåðöèé ñå÷åíèé íàèáîëåå ðàñïðîñòðàíåííûõ ïðîôèëåé
Óñòîé÷èâîñòü ñòåðæíåé ïðè ñæàòèè
Íåêîòîðûå ýëåìåíòû êîíñòðóêöèè ÑËÀ, â ÷àñòíîñòè ñòîéêè, ïîäêîñû, ñòåðæíè ôåðì, òÿãè ñèñòåì óïðàâëåíèÿ, ìîãóò ïîäâåðãàòüñÿ ïðîäîëüíîìó èçãèáó. Òàêîé èçãèá ïðîèñõîäèò ïîä äåéñòâèåì ñèëû, íàïðàâëåííîé âäîëü îñè ñæèìàåìîãî ýëåìåíòà. Äàæå ïðè ïîñòåïåííîì óâåëè÷åíèè äåéñòâóþùåé ñèëû ìîæåò íàñòóïèòü ìîìåíò îáùåé èëè ìåñòíîé ïîòåðè óñòîé÷èâîñòè. Ïðè îáùåé ïîòåðå óñòîé÷èâîñòè ïðîèñõîäèò èñêðèâëåíèå îñè ýëåìåíòà, ñ ðåçêèì ïàäåíèåì âîñïðèíèìàåìîé ýëåìåíòîì íàãðóçêè. Ìåñòíîé ïîòåðè óñòîé÷èâîñòè ïîäâåðæåíû óãîëêè, øâåëëåðû, Z-îáðàçíûå è äðóãèå ïðîôèëè ñëîæíîé êîíôèãóðàöèè. Ïðè ìåñòíîé ïîòåðå óñòîé÷èâîñòè ïðîèñõîäèò âûïó÷èâàíèå, èçëîì èëè ïîÿâëåíèå ãîôðà íà êàêîì-ëèáî ýëåìåíòå ñëîæíîãî ïðîôèëÿ.
Âåëè÷èíà êðèòè÷åñêîé ñèëû, ïðè êîòîðîé ïðîèñõîäèò îáùàÿ ïîòåðÿ óñòîé÷èâîñòè ñòåðæíÿ ïîñòîÿííîãî ñå÷åíèÿ, îïðåäåëÿåòñÿ ôîðìóëîé Ýéëåðà
ãäå ñ — êîýôôèöèåíò çàäåëêè êîíöîâ ñòåðæíÿ; Jmin — ìèíèìàëüíûé îñåâîé ìîìåíò èíåðöèè ñòåðæíÿ; l-ïîëíàÿ äëèíà ñòåðæíÿ.
Åñëè îáà êîíöà ñòåðæíÿ çàêðåïëåíû øàðíèðíî, òî ñ=1, åñëè îáà èìåþò æåñòêóþ (ìîìåíòíóþ) çàäåëêó, òî ñ=4. Åñëè îäèí êîíåö ñòåðæíÿ çàäåëàí æåñòêî, à äðóãîé øàðíèðíî, òî c=2. Íà ïðàêòèêå â êîíêðåòíîé êîíñòðóêöèè íå âñåãäà óäàåòñÿ îïðåäåëèòü âèä çàäåëêè. À òàê êàê êîýôôèöèåíò çàäåëêè ìåíÿåòñÿ â øèðîêèõ ïðåäåëàõ, òî óñëîâèÿ íà îïîðàõ èìåþò áîëüøîå çíà÷åíèå è äîëæíû êàæäûé ðàç âñåñòîðîííå îöåíèâàòüñÿ. Ïðè ñîìíåíèè â ïðàâèëüíîñòè îïðåäåëåíèÿ âèäà çàäåëêè íåîáõîäèìî áðàòü áîëåå íèçêîå çíà÷åíèå ñ.
Íà ïðàêòèêå óäîáíåå îïðåäåëÿòü íå êðèòè÷åñêóþ ñèëó, à êðèòè÷åñêîå íàïðÿæåíèå. Åãî ìîæíî îïðåäåëèòü ïî ôîðìóëå
 êîíñòðóêöèè ÑËÀ ïðîäîëüíîìó èçãèáó ÷àùå âñåãî ïîäâåðãàþòñÿ ñòåðæíè, ñå÷åíèå êîòîðûõ ïðåäñòàâëÿåò êðóã, êîëüöî, ïðÿìîóãîëüíèê è êàïëåâèäíîå îáòåêàåìîå òåëî. Ôîðìóëû äëÿ îïðåäåëåíèÿ êðèòè÷åñêèõ íàïðÿæåíèé ñòåðæíåé ïåðå÷èñëåííûõ âûøå ñå÷åíèé ïðèâåäåíû â òàáë. 3. 8.
Òàáëèöà 3.8 Ôîðìóëû äëÿ îïðåäåëåíèÿ êðèòè÷åñêèõ íàïðÿæåíèé ñæàòèÿ ñòåðæíåé ðàçëè÷íûõ ñå÷åíèé
Äëÿ îïðåäåëåíèÿ êðèòè÷åñêèõ íàïðÿæåíèé òðóá èç Ä-16 è ÇÎÕÃÑÀ ìîæíî âîñïîëüçîâàòüñÿ ãðàôèêàìè, ïðåäñòàâëåííûìè íà ðèñ. 3.5, à, á, à ïðÿìîóãîëüíûõ ñòåðæíåé èç ñîñíû — ãðàôèêîì, ïðåäñòàâëåííûì íà ðèñ. 3.5, â.
Ðèñ 3.5 Ê îïðåäåëåíèþ êðèòè÷åñêèõ íàïðÿæåíèé â ìàòåðèàëå ïðè ïðîäîëüíîì èçãèáå
Ñëåäóåò èìåòü â âèäó, ÷òî íåñîâåðøåíñòâî èçãîòîâëåíèÿ ñòåðæíåé èëè ìàëåéøèå èõ äåôîðìàöèè, ïðèâîäÿùèå ê ïîÿâëåíèþ íà÷àëüíîé êðèâèçíû, ðåçêî óìåíüøàþò êðèòè÷åñêèå íàïðÿæåíèÿ.
Êðèòè÷åñêèå íàïðÿæåíèÿ èç óñëîâèÿ ìåñòíîé ïîòåðè óñòîé÷èâîñòè óãîëêà èç Ä-16 ìîæíî ñíÿòü ñ ãðàôèêà ðèñ. 3.5, ã.
ïî ìàòåðèàëàì: Ï.È.×óìàê, Â.Ô Êðèâîêðûñåíêî «Ðàñ÷åò è ïðîåêòèðîâàíèå ÑËÀ»
Источник
