Растяжение графика квадратичной функции

Список функций, изученных в 7 и 8 классе
Функция | Формула | График | Раздел справочника |
Прямая пропорциональность | y = kx | Прямая | 7 кл., §37 |
Линейная функция | y = kx+b | Прямая | 7 кл., §38-39 |
Обратная пропорциональность | $ y = frac{k}{x} $ | Гипербола | 8 кл., §6 |
Квадрат числа | $ y=x^2$ | Парабола | 8 кл., §18 |
Квадратный трёхчлен | $ y = ax^2+bc+c$ | Парабола | 8 кл., §28-29 |
Квадратный корень | $ y = sqrt{x}$ | Парабола | 8 кл., §22 |
Растяжение и сжатие графика по оси OX
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), y_2 = f(px) $$
где $p gt 1$, произвольный положительный множитель.
Пусть p = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f(2x) = (2x)^2 = 4x^2 $ $y_2 = y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f(2x) = frac{4}{(2x)} = frac{2}{x}$ $ y_2 = y_1 при x_2 = frac{1}{2} x_1 $ График сжимается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f(2x) = sqrt{2x}$ $y_2=y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |
|
Теперь сравним пары функций с делением на p:
$$ y_1 = f(x), quad y_2 = f left( frac{x}{p} right), quad p gt 1 $$
Пусть p = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f left(frac{x}{2}right) = left(frac{x}{2}right)^2 = frac{x^2}{4} $ $y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f left(frac{x}{2}right) = frac{4}{x/2} = frac{8}{x}$ $ y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f left(frac{x}{2}right) = sqrt{frac{x}{2}}$ $y_2=y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f(px), quad p gt 1 $$
график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f Biggl(frac{x}{p}Biggr), quad p gt 1 $$
график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Растяжение и сжатие графика по оси OY
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), quad y_2 = Af(x) $$
где $A gt 1$, произвольный положительный множитель.
Пусть A = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = 2f(x) = 2x^2 $ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = 2f(x) = frac{8}{x}$ $ y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = 2f(x) = 2sqrt{x}$ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Теперь сравним пары функций с делением на A:
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
Пусть A = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = frac{1}{2}f(x) = frac{x^2}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = frac{1}{2}f(x) = frac{2}{x}$ $ y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = frac{1}{2}f(x) = frac{sqrt{x}}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = Af(x), quad A gt 1 $$
график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Примеры
Пример 1. Постройте в одной координатной плоскости графики функций:
$$ y = sqrt{x}, y = sqrt{3x}, y = sqrt{frac{x}{3}}, y = 3sqrt{x} $$
Сделайте выводы.

По сравнению с графиком $y = sqrt{x}$:
- график функции $y = sqrt{3x}$ сжимается в 3 раза по оси OX(←)
- график функции $y = sqrt{frac{x}{3}}$ растягивается в 3 раза по оси OX(→)
- график функции $y = 3sqrt{x}$ растягивается в 3 раза по оси OY(↑)
Пример 2*. Постройте в одной координатной плоскости графики функций:
$$ y = f(x), y = f(2x), y = f Biggl(frac{x}{2}Biggr), y = 2f(x) $$
где $f(x) = x^2+3x+2$
Сделайте выводы.
Исходная функция $y = f(x) = x^2+3x+2$
Остальные функции
$$ y = f(2x) = (2x)^2+3 cdot (2x)+2 = 4x^2+6x+2 $$
$$ y = fBiggl(frac{x}{2}Biggr) = Biggl(frac{x}{2}Biggr)^2+3 cdot Biggl(frac{x}{2}Biggr) +2 = frac{x^2}{4}+ frac{3}{2} x+2 $$
$$ y = 2f(x) = 2x^2+6x+4 $$
Получаем:

По сравнению с графиком $y = f(x) = x^2+3x+2$:
- график функции y = f(2x) сжимается в 2 раза по оси OX(→)
- график функции $y = f left(frac{x}{2}right)$ растягивается в 2 раза по оси OX(←)
- график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)
Рейтинг пользователей
85
Best gift

80
Елена Зайцева
75
FixEye:3

70
Анна Скоробогатова
50
Источник
Тема 4.
Всем привет! Сегодня мы поговорим об одной из самых важных функций, о квадратичной функции.
Квадратичной функцией называется функция, которую можно задать y = ax2 + bx + c, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0.
Изучение квадратичной функции мы начнем с частного случая, а именно с функции y = ax2. Мы уже встречались с функцией y = x2, когда a = 1. Ее графиком является парабола.
Построим в одной системе координат
y = x2; y = 2x2; y = 3x2.
y = x2
x | -3 | -2 | -1 | 1 | 2 | 3 |
y | 9 | 4 | 1 | 1 | 4 | 9 |
y = 2x2
x | -3 | -2 | -1 | 1 | 2 | 3 |
y | 18 | 8 | 2 | 2 | 8 | 18 |
При любом x ≠ 0 значение функции y = x2 в 2 раза больше соответствующих значений функции y = x2. То есть график функции y = x2 можно получить из параболы y = x2 растяжением от оси x в 2 раза.
Аналогично, график функции y = 3x2 можно получить из графика функции y = x2 растяжением от оси x в 3 раза.
Построим теперь в одной системе координат графики функции y = x2, y=12×2, y=13×2.
y=12×2
x | -3 | -2 | -1 | 1 | 2 | 3 |
y | 4,5 | 2 | 0,5 | 0,5 | 2 | 4,5 |
Заметим, что при любом x ≠ 0 значения функции y=12×2меньше соответствующих значений функции y = x2 в 2 раза.
Таким образом, график функции y=12×2 можно получить из параболы y = x2 сжатием к оси x в 2 раза.
y=13×2
x | -3 | -2 | -1 | 1 | 2 | 3 |
y | 3 | 43 | 13 | 13 | 43 | 3 |
Аналогично график функции y=13×2 можно получить из графика функции = x2 сжатием к оси x в 3 раза.
Давай сделаем вывод:
График функции y = ax2 можно получить из параболы y = x2 растяжением от оси x в a раз, если a > 1, и сжатием к оси x в 1a раз, если 0 a
Рассмотрим теперь случай, когда a y=-13×2. Составим таблицу значений:
x | -3 | -2 | -1 | 1 | 2 | 3 |
y | -3 | -43 | -13 | -13 | -43 | -3 |
Сравним графики функций y=13×2 и y=-13×2. При любом x ≠ 0 значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси x.
То есть графики функций y = ax2 и y = —ax2 при a ≠ 0 симметричны относительно оси x. Графиком функции y = ax2, как и графиком функции y = x2 является парабола
Сформулируем свойства функции y = ax2 при a > 0.
- Область определения -∞;+∞;
- Область значений функций 0;+∞
- Если x = 0, то y = 0, т.е. график функции проходит через начало координат.
- Если x ≠ 0, то y > 0. График функции расположен в верхней полуплоскости.
- График функции симметричен относительно оси y.
- Функция убывает в промежутке -∞;0 и возрастает в промежутке 0;+∞.
- При x = 0 функция принимает наименьшее значение, равное 0. Наибольшего значения функции нет.
Сформулируем свойства функции y = ax2 при a
- Область определения -∞;+∞;
- Область значений функций -∞;0
- Если x = 0, то y = 0, т.е. график функции проходит через начало координат.
- Если x ≠ 0, то y
- График функции симметричен относительно оси y.
- Функция убывает в промежутке 0;+∞ и возрастает в промежутке -∞;0.
- При x = 0 функция принимает наибольшее значение, равное 0. Наименьшего значения функции нет.
От коэффициента a зависит направление ветвей параболы. Если a > 0, то ветви параболы направлены вверх, если a
Построение графика, симметричного данному относительно оси x, или сжатие к оси x – различные виды преобразований графиков функций. Преобразования графиков функции, рассмотренные нами сегодня для функций y = ax2, применимы к любой функции.
График функции y=-fx можно получить из графика функции y=fx с помощью симметрии относительно оси абсцисс.
График функции y=afx можно получить из графика функции y=fx с помощью растяжения от оси x в a раз, если a > 1, и сжатием к оси x в 1a раз, если 0
Источник
Цели урока:
- Актуализация знаний, умений и навыков учащихся
по теме “Квадратичная функция”. - Развитие творческого математического мышления,
исследовательских навыков учащихся. - Подготовка к экзамену.
Оборудование:
- мультимедиа;
- раздаточный материал;
- учебник алгебры.
Приложение. Презентация.
ХОД УРОКА
1. Организационный момент.
Учитель объявляет тему урока, ставит цели и
задачи перед учащимися, сообщает план урока:
- Устный опрос учащихся.
- Проверка домашнего задания.
- Устная работа.
- Решение экзаменационных заданий.
- Контрольно-обобщающий тест.
- Итоги и выводы по уроку.
Приложение 1. Слайд № 1 (название урока).
На прошлом уроке мы повторили свойства
квадратичной функции, вспомнили, как строится
график функции по точкам и с помощью
преобразований графиков. Повторили решение
неравенств второй степени. Сегодня мы обобщим
весь материал и перейдем к решению более сложных
задач.
Устный опрос учащихся.
Вы знаете, что каждый коэффициент в записи
функции нам может многое рассказать. Итак,
старший коэффициент а?
Если а>0, то ветви параболы направлены вверх,
если а < 0, то вниз. Если | а | > 1, то растяжение
графика от оси абсцисс, если | а | < 1, то сжатие к
оси абсцисс.
Свободный член с?
Точка пересечения графика с осью y имеет
координату (0, с).
Также можно найти дискриминант квадратного
трехчлена. Если D > 0, то у параболы две точки
пересечения с осью x, если D = 0, то одна точка
пересечения, если D < 0, то точек пересечения нет.
А еще можно найти координаты вершины параболы,
абсцисса которой находится по формуле .
Проверка домашнего задания.
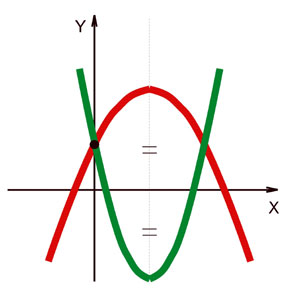 В
В
домашней работе у вас был очень интересный, на
мой взгляд, номер с двумя параболами.
Приложение 1. Слайд № 2.
На рис. 1 изображены две параболы, уравнение
одной из них y=ax2+bx+c. Какое из следующих
уравнений имеет вторая парабола?
А) y= -x2 -bx+c
Б) y= -2ax2+bx+c
В) y= -2ax2+2bx-c
Г) y= -2ax2-2bx+c
Д) y= -ax2+bx-c.
Решение. Параболы пересекают ось ОУ в одной
точке, значит знак перед свободным членом должен
быть “+”. У параболы, ветви которой направлены
вверх, старший коэффициент по модулю больше, чем
у другой. Так как, модулей старших коэффициентов
только два | а | и | 2а |, значит, ветви параболы y = ax2
+ bx + c направлены вниз, а у искомой параболы
старший коэффициент равен -2а. вершины параболы
симметричны относительно оси ОХ, значит,
отношение второго коэффициента к старшему
должны быть одинаковыми. Ответ Г).
Устная работа.
На экране будут показаны задания. Ответы вы
записываете в тетрадь. После проверки, в конце
работы, сами поставите оценки.
Приложение 1. Слайд № 3; 4; 5.
Решение экзаменационных заданий.
Переходим к решению более сложных и интересных
задач.
У вас на столах карточки с заданиями из
сборника экзаменационных задач и учебник
алгебры авторов Муравиных.
№ 220 (из учебника). При каких значениях k
неравенство 2×2 – 6x + k > 0
а) Верно при любом значении x?
б) Верно при всех значениях, кроме одного?
в) Неверно ни при каком значении x?
Решение. а) Рассмотрим функциюy = 2×2 – 6x + k,
графиком является парабола, ветви направлены
вверх. Для того, чтобы неравенство было верным
при любом значении x, необходимо, чтобы у параболы
не было точек пересечения с осью x. Это
выполняется при D < 0, D = 36 – 8k, k > 4,5. Ответ. (4,5; ).
б) k = 4,5.
в) Таких решений нет.
Раздаточный материал составлен из заданий
сборника экзаменационных задач для 9-го класса. К
доске вызываются трое учащихся для решения
номеров из карточек под номером 1) Те ребята,
которые успевают сделать и задания под номером 2)
получают дополнительные оценки.
№ 18.
1) При каких значениях a парабола y = ax2 – 2x
– 3 пересекает ось x в двух точках и ее ветви
направлены вниз?
2) при каких значениях a парабола y = ax2 – 3x +
1 пересекает ось x в двух точках и ее ветви
направлены вверх?
№ 28.
1) При каких положительных значениях k парабола y
= x2 + x – 1 и прямая y = kx — 2 не пересекаются?
2) Найдите все положительные значения k, при
которых прямая y = kx – 7 пересекает параболу y = x2
+ 2x – 3 в двух точках.
№ 32.
1) 2) Найдите координаты точек, в которых
парабола, изображенная на рисунке (с. 129 сборника
экзаменационных задач для 9 класса), пересекает
ось x.
Контрольно-обобщающий тест.
Приложение 1. Слайд № 6.
Итоги и выводы по уроку.
Сегодня на уроке мы закончили повторение
свойств квадратичной функции. Мне хотелось бы
услышать, что нового вы открыли для себя. Мне
кажется, сегодня вы смогли подняться еще на
ступеньку вверх по сложной лестнице под
названием “Математика”. На собственном опыте
убедились, что, обладая необходимыми знаниями,
можно решать и достаточно сложные задания с
параметрами.
Домашнее задание.
Сборник экзаменационных заданий: №№ 19, 29, 31, 33.
Источник
Цели урока:
Образовательная: исследовать смещение
графика квадратичной функции, определить
положение графика в зависимости от значений
коэффициентов b, c.
Воспитательная: умение работать в группе,
организованности.
Развивающая: навыки исследовательской
работы, умение выдвигать гипотезы, анализировать
полученные результаты, систематизировать
полученные данные.
Структура урока
- Организационный момент – 3 минуты.
- Исследовательская работа – 20 минут.
- Закрепление изученного материала – 15 минут.
- Рефлексия – 2 минут.
- Итог урока – 3 минуты.
- Домашнее задание – 2 минуты.
Ход урока
1. Организационный момент.
Цель урока провести исследовательскую работу.
Объектом исследования будут квадратичные
функции разного вида. Вам предстоит определить,
как влияют коэффициенты b, cна график
функций вида y=x2+с, y=(x-b)2, y=(x-b)2+c.
Для выполнения задания необходимо разделиться
на группы (4 группы по 5 человек, одна группа
“эксперты” наиболее подготовленные ученики).
Каждая группа получает план исследования
<Приложение>, лист формата А3 для оформления
результатов.
2. Исследовательская работа
.
Две группы (уровень А) исследуют функции вида y= x2+с,
одна группа (уровень В) исследует функцию вида
y=(x-b)2, одна группа (уровень С) исследует
функцию y=(x-b)2+c. Группа “Экспертов”
исследует все функции.
План работы
- Для того чтобы выдвинуть гипотезу сделайте
предположение, как может выглядеть ваша функция. - Постройте график исследуемых функций
(определите вершину параболы (х0, y0),
задайте таблицей 4 точки). - Сравните получившийся график с контрольным
образцом y=x2. - Сделайте вывод (как изменилось положение
графика вашей функции относительно контрольного
образца). - Результаты оформите на листе формата А3 и
представьте “экспертной” группе.
“Экспертная” группа сверяет результаты свои с
результатами остальных групп, систематизирует и
обобщает результаты, выступает с выводами. В
случае неточностей или ошибок учитель вносит
коррекционные замечания.
Сверка полученных результатов со слайдами
№2-5.
Любую квадратичную функцию y=ax2+bx+c, можно
записать в виде y=a(x-x0)2+y0, где x0
и y0 выражаются через коэффициенты a, b, c.
Таким образом, ваши коэффициенты b=x0, c=y0
являются координатами вершины параболы.
3. Закрепление изученного материала.
Фронтальная работа с классом.
1. Найти ошибку в графиках функций (Слайды№6-9).
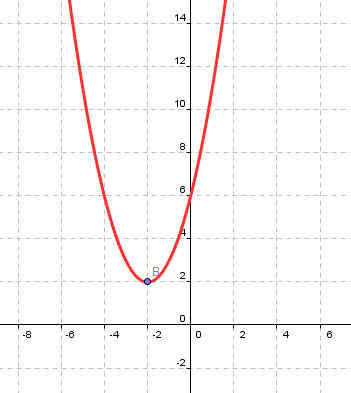
y=(х+6)2 | у=х2-2 |
Коэффициент b | Нет ошибки |
Рисунок 1 | Рисунок 2 |
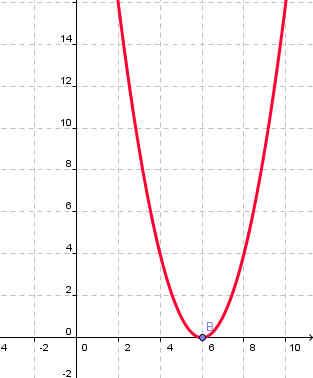 | 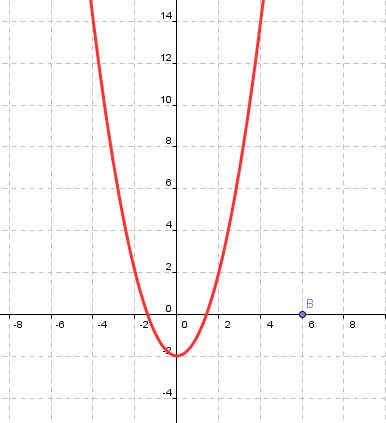 |
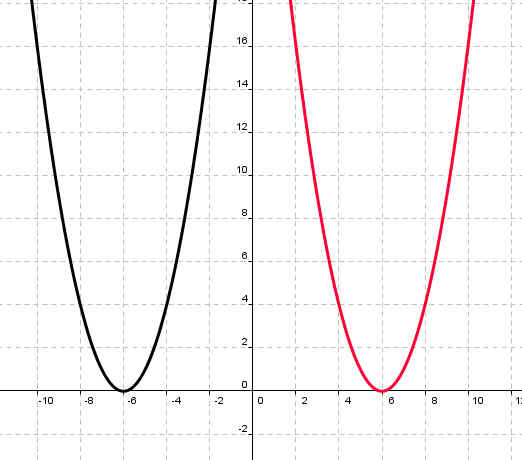
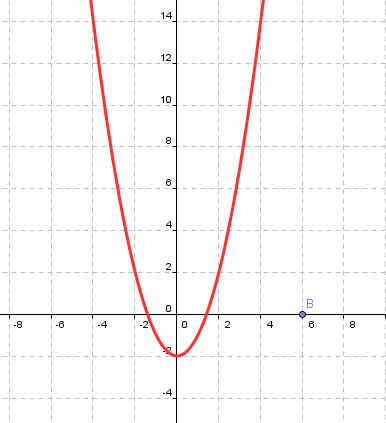
| у=(х+5)2-1 | у=(х-2)2+2 |
| Коэффициент b и с | Коэффициент b |
| Рисунок 3 | Рисунок 4 |
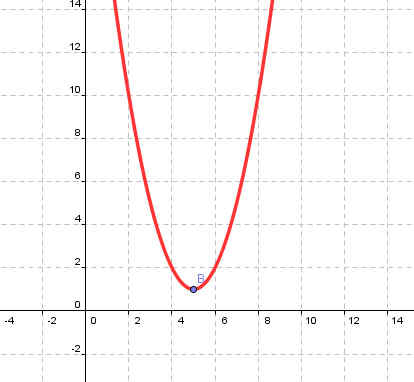 |  |
Результаты
<Рисунок 7>
<Рисунок 2>
<Рисунок 8>
<Рисунок 9>
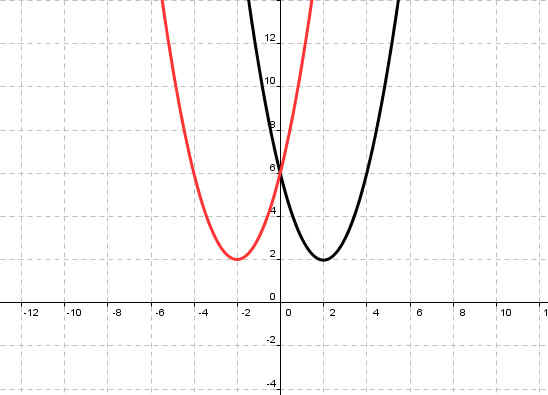
Какой коэффициент вам помог найти ошибку?
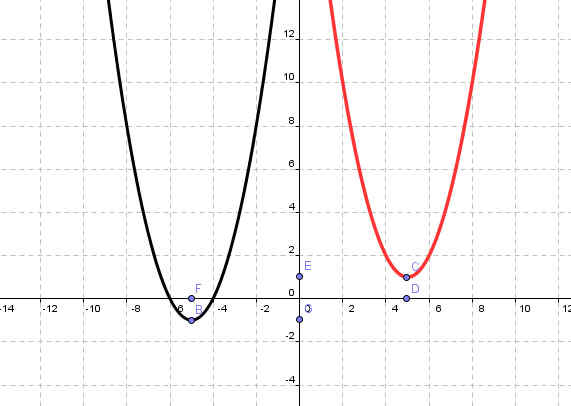
2. Соотнесите графики функций согласно цветам (слайд
№10).
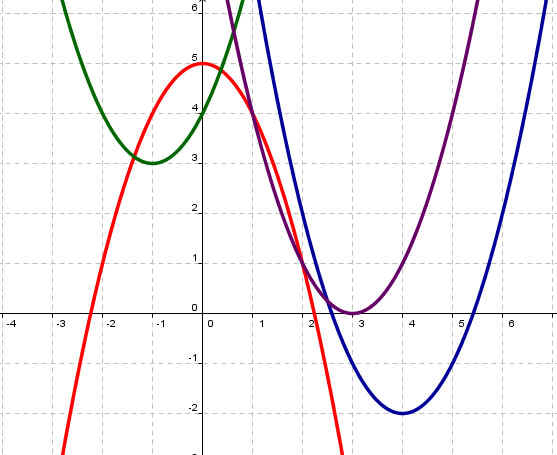
Рисунок 5
| y=(х-4)2-2 | синий |
| y=-x2+5 | красный |
| y=(x+1)2+3 | зеленый |
| y=(x-3)2 | фиолетовый |
4. Рефлексия.
Группа “Экспертов” отвечают на вопросы:
– Какие ошибки допустили группы?
– Достигнута ли цель занятия?
– Соответствуют ли полученные результаты
исследования поставленной гипотезе?
5. Итог урока (слайд №11)
:
На положение графика функции y=(x-b)2+c
влияют коэффициенты b и c,
“+b” парабола сдвинута вправо по оси абсцисс на
b единичных отрезков,
“–b” парабола сдвинута влево по оси абсцисс на
b единичных отрезков,
“+с” парабола сдвинута вверх по оси ординат на
с единичных отрезков,
“-с” парабола сдвинута вниз по оси ординат на с
единичных отрезков.
6. Домашнее задание
- Построить график квадратичной функции, имеющую
вершину в точке А(1;-2), коэффициент a=1. - Подумайте, в какой области можно использовать
знания по данной теме (практическое применение).
Приложение
Источник








