Растяжение графика функции вдоль оси ординат
Список функций, изученных в 7 и 8 классе
Функция | Формула | График | Раздел справочника |
Прямая пропорциональность | y = kx | Прямая | 7 кл., §37 |
Линейная функция | y = kx+b | Прямая | 7 кл., §38-39 |
Обратная пропорциональность | $ y = frac{k}{x} $ | Гипербола | 8 кл., §6 |
Квадрат числа | $ y=x^2$ | Парабола | 8 кл., §18 |
Квадратный трёхчлен | $ y = ax^2+bc+c$ | Парабола | 8 кл., §28-29 |
Квадратный корень | $ y = sqrt{x}$ | Парабола | 8 кл., §22 |
Растяжение и сжатие графика по оси OX
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), y_2 = f(px) $$
где $p gt 1$, произвольный положительный множитель.
Пусть p = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f(2x) = (2x)^2 = 4x^2 $ $y_2 = y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f(2x) = frac{4}{(2x)} = frac{2}{x}$ $ y_2 = y_1 при x_2 = frac{1}{2} x_1 $ График сжимается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f(2x) = sqrt{2x}$ $y_2=y_1 при x_2 = frac{1}{2} x_1$ График сжимается в 2 раза по оси OX |
|
Теперь сравним пары функций с делением на p:
$$ y_1 = f(x), quad y_2 = f left( frac{x}{p} right), quad p gt 1 $$
Пусть p = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = f left(frac{x}{2}right) = left(frac{x}{2}right)^2 = frac{x^2}{4} $ $y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = f left(frac{x}{2}right) = frac{4}{x/2} = frac{8}{x}$ $ y_2 = y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = f left(frac{x}{2}right) = sqrt{frac{x}{2}}$ $y_2=y_1 при x_2 = 2x_1$ График растягивается в 2 раза по оси OX |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f(px), quad p gt 1 $$
график второй функции сжимается в p раз по оси OX по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = f Biggl(frac{x}{p}Biggr), quad p gt 1 $$
график второй функции растягивается в p раз по оси OX по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Растяжение и сжатие графика по оси OY
Сравним графики пар функций, которые в общем виде можно записать так:
$$ y_1 = f(x), quad y_2 = Af(x) $$
где $A gt 1$, произвольный положительный множитель.
Пусть A = 2.
Парабола: $y_1 = f(x) = x^2$ $ y_2 = 2f(x) = 2x^2 $ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = 2f(x) = frac{8}{x}$ $ y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = 2f(x) = 2sqrt{x}$ $y_2 = 2y_1 при x_2 = x_1$ График растягивается в 2 раза по оси OY |
|
Теперь сравним пары функций с делением на A:
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
Пусть A = 2
Парабола: $y_1 = f(x) = x^2$ $ y_2 = frac{1}{2}f(x) = frac{x^2}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |  |
Гипербола: $ y_1 = f(x) = frac{4}{x}$ $y_2 = frac{1}{2}f(x) = frac{2}{x}$ $ y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
Квадратный корень: $y_1 = f(x) = sqrt{x}$ $y_2 = frac{1}{2}f(x) = frac{sqrt{x}}{2}$ $y_2 = frac{1}{2}y_1 при x_2 = x_1$ График сжимается в 2 раза по оси OY |
|
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = Af(x), quad A gt 1 $$
график второй функции растягивается в A раз по оси OY по сравнению с графиком первой функции.
При сравнении графиков двух функций
$$ y_1 = f(x), quad y_2 = frac{1}{A} f(x), quad A gt 1 $$
график второй функции сжимается в A раз по оси OY по сравнению с графиком первой функции.
Заметим, что данные утверждения справедливы не только для рассмотренных функций, но и для любых других (синусов, косинусов, логарифмов и т.п.)
Примеры
Пример 1. Постройте в одной координатной плоскости графики функций:
$$ y = sqrt{x}, y = sqrt{3x}, y = sqrt{frac{x}{3}}, y = 3sqrt{x} $$
Сделайте выводы.
По сравнению с графиком $y = sqrt{x}$:
- график функции $y = sqrt{3x}$ сжимается в 3 раза по оси OX(←)
- график функции $y = sqrt{frac{x}{3}}$ растягивается в 3 раза по оси OX(→)
- график функции $y = 3sqrt{x}$ растягивается в 3 раза по оси OY(↑)
Пример 2*. Постройте в одной координатной плоскости графики функций:
$$ y = f(x), y = f(2x), y = f Biggl(frac{x}{2}Biggr), y = 2f(x) $$
где $f(x) = x^2+3x+2$
Сделайте выводы.
Исходная функция $y = f(x) = x^2+3x+2$
Остальные функции
$$ y = f(2x) = (2x)^2+3 cdot (2x)+2 = 4x^2+6x+2 $$
$$ y = fBiggl(frac{x}{2}Biggr) = Biggl(frac{x}{2}Biggr)^2+3 cdot Biggl(frac{x}{2}Biggr) +2 = frac{x^2}{4}+ frac{3}{2} x+2 $$
$$ y = 2f(x) = 2x^2+6x+4 $$
Получаем:
По сравнению с графиком $y = f(x) = x^2+3x+2$:
- график функции y = f(2x) сжимается в 2 раза по оси OX(→)
- график функции $y = f left(frac{x}{2}right)$ растягивается в 2 раза по оси OX(←)
- график функции y = 2f(x) растягивается в 2 раза по оси OY(↑)
Рейтинг пользователей
50
timoelena
50
mmm_777
50
daria.sergutina
50
Елена Муравьева
50
Антон Антонов
Источник
Ìàñøòàáèðîâàíèå — îïåðàöèÿ ñæàòèÿ èëè ðàñòÿæåíèÿ ãðàôèêà ôóíêöèè âäîëü îñåé àáñöèññ è îðäèíàò.
Òî, ÷òî òðåáóåòñÿ âûïîëíèòü ìàñøòàáèðîâàíèå, ïîêàçûâàþò êîýôôèöèåíòû k1 è k2 â óðàâíåíèè y = ± k1 f (± k2 (x + a))+b. Îíè äîëæíû áûòü íå ðàâíû åäèíèöå.
Êîãäà 0 < k1,2 <1, ñîâåðøàåì ñæàòèå ãðàôèêà îòíîñèòåëüíî y è ðàñòÿæåíèå îòíîñèòåëüíî x , êîãäà k1,2>1, âûïîëíÿåì ðàñòÿæåíèå âäîëü îñè îðäèíàò è ñæàòèå âäîëü îñè àáñöèññ.
Êîãäà ôóíêöèÿ ïðèíèìàåò âèä y = f (k2x) ,òî åñëè k2 >1 – ïðîèçâîäèì ñæàòèå ãðàôèêà ê îñè îðäèíàò (y) â k ðàç, à åñëè 0 < k2<1 — ðàñòÿæåíèå ãðàôèêà îò îñè îðäèíàò â 1/k.
Êîãäà ôóíêöèÿ ïðèíèìàåò âèä y = k1 f (x) , òî åñëè k1 >1 — îñóùåñòâëÿåì ðàñòÿæåíèå ãðàôèêà îò îñè àáñöèññ (0x) â k ðàç, à åñëè 0 < k1<1 — ñæàòèå ãðàôèêà ê îñè àáñöèññ â 1/k.
Êàëüêóëÿòîðû ïî àëãåáðå | |
| Ðåøåíèÿ, ïîäñêàçêè è ó÷åáíèê ëèíåéíîé àëãåáðû îíëàéí (âñå êàëüêóëÿòîðû ïî àëãåáðå). | |
| Êàëüêóëÿòîðû ïî àëãåáðå | |
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó àëãåáðû äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãðàôèêè ýëåìåíòàðíûõ ôóíêöèé | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ìàòåìàòèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãðàôèêè ýëåìåíòàðíûõ ôóíêöèé | |
Ôóíêöèÿ. Ïîêàçàòåëüíàÿ ôóíêöèÿ. | |
| Ïîêàçàòåëüíîé íàçûâàåòñÿ ôóíêöèÿ ó = à õ , â êîòîðîé à ýòî ïîñòîÿííîå ïîëîæèòåëüíîå ÷èñëî. | |
| Ôóíêöèÿ. Ïîêàçàòåëüíàÿ ôóíêöèÿ. | |
Ôóíêöèÿ. Ëèíåéíûå ôóíêöèè. | |
| Åñëè ïåðåìåííûå õ, ó âûðàæàþòñÿ ïîñðåäñòâîì óðàâíåíèÿ Àõ + By = Ñ , ïðè ýòîì ÷èñëà À,  èëè ïî ìåíüøåé ìåðå îäíî èç íèõ, íå ðàâíî íóëþ, òî ãðàôèêîì ôóíêöèîíàëüíîé çàâèñèìîñòè ÿâëÿåòñÿ ïðÿìàÿ ëèíèÿ . | |
| Ôóíêöèÿ. Ëèíåéíûå ôóíêöèè. | |
Источник
3.1 Сжатие (растяжение) графика вдоль оси ординат
Рассмотрим
функцию вида y=A
,
где A>0.
Нетрудно заметить, что при равных
значениях аргумента ординаты графика
этой функции будут в A
раз больше ординат графика функции
y=f(x)
при A>1
или в
раз меньше ординат графика функцииy=f(x)
при A<1.
Таким образом, получаем следующее
правило.
Для
построения графика функции y=A
следует построить график функции y=f(x)
и увеличить его ординаты в A
раз при A>1
(произвести растяжение графика вдоль
оси ординат) или уменьшить его ординаты
в
раз приA<1
(произвести сжатие графика вдоль оси
ординат). Полученный график является
графиком функции y=A
.
Пример
13. Построить
график функции y=2cos
x.
Р
е ш е н и е: Строим график функции y=cos
x
(рис.16 – пунктирная кривая) и растяжением
этого графика вдоль оси ординат в 2
раза получаем график функции y=2cos
x
(сплошная кривая).
Пример
14. Построить
график функции y=
x2.
Р
е ш е н и е: Строим график функции y=x2
и сжатием этого графика в 3 раза вдоль
оси ординат получаем график функции
y=
x2
(рис.17).
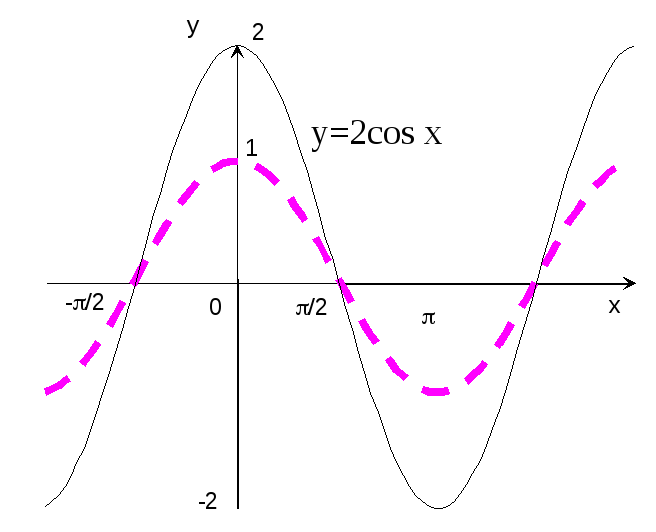
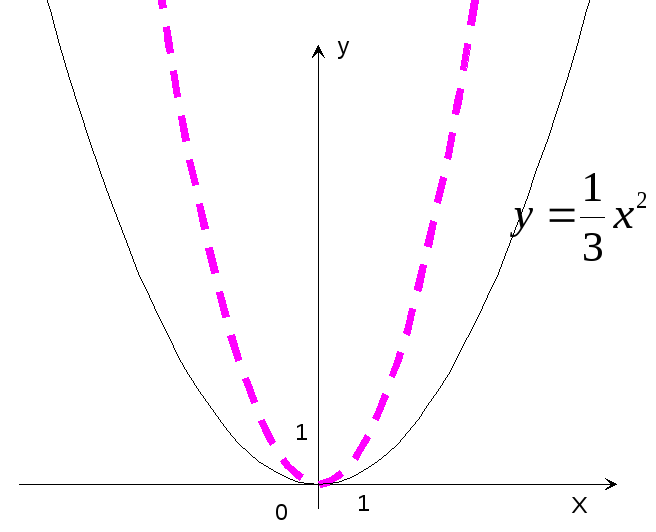
Рис.16
Рис.17
3.2. Сжатие (растяжение) графика вдоль оси абсцисс
Пусть
требуется построить график функции
y=f(x),
где >0.
Рассмотрим функцию y=f(x),
которая в произвольной точке x=x1
принимает значение y1=f(x1).
Очевидно,
что функция y=f(x)
принимает такое же значение в точке
x=x2,
координата
к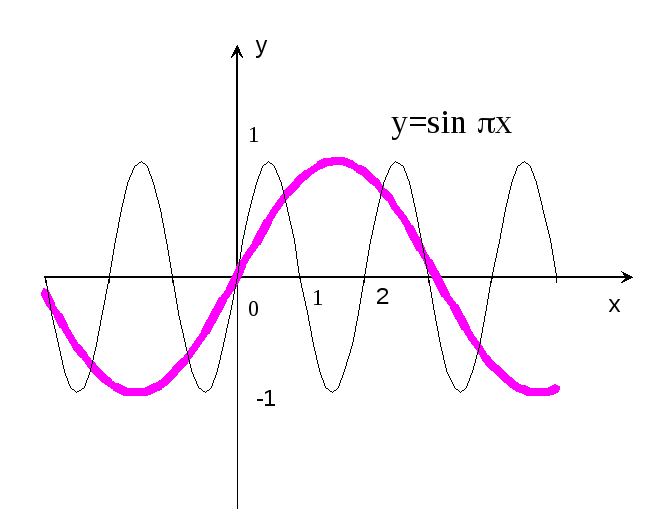
оторой
определяется равенствомx1=x2,
или x2=
,
причём это равенство справедливо для
совокупности всех значений x
из области определения функции.
Следовательно, график функции y=f(x)
оказывается сжатым (при >1)
или растянутым (при <1)
вдоль оси абсцисс относительно графика
функции y=f(x).
Таким образом, получаем следующее
правило.
Для
построения графика функции y=f(x)
следует построить график функции y=f(x)
и уменьшить его абсциссы в
раз при >1
(произвести сжатие графика вдоль оси
абсцисс) или увеличить его абсциссы в
раз при<1
(произвести растяжение графика вдоль
оси абсцисс). Полученный график является
графиком функции y=f(x).
П
Рис. 18
ример 15.Построить
график функции
x.
Р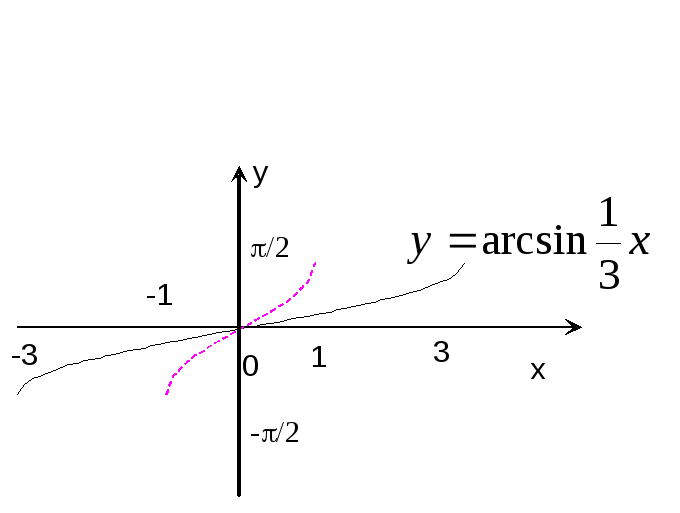
е ш е н и е: Строим график функции
x
(рис.18 – пунктирная кривая), и проводя
его сжатие в
раз вдоль оси абсцисс, получаем график
функции
x
(сплошная кривая). Период этой функции
уже равен не 2,
а
=2.
График пересекает ось абсцисс в точкахx=0,
…
.
Пример
16. Построить
график функции
.
Р
е ш е н и е: Строим график функции
и, растянув его вдоль оси абсцисс в 3
раза, получаем график функции
.
4. Комбинация переноса, отражения и деформации
Рис.
19
Очень часто при построении графиков
функций применяют композицию приёмов,
изложенных в пунктах 1-3. Последовательное
применение ряда таких приёмов позволяет
существенно упростить построение
графика исходной функции и нередко
свести его в конце концов к построению
одной из простейших элементарных
функций.
Рассмотрим,
как с учётом изложенного следует,
например, построить
график функции вида y=Af(x+a)+b.
Запишем
исходную функцию в виде y=Af
[
( x+
) ] +b
и схему поэтапного её упрощения
(последовательность преобразований):
1
.y=Af
[
( x+
) ] + b
; перенос оси абсцисс на b
единиц;
2
.y=Af
[
( x+
) ]; перенос оси ординат на
единиц;
3. y=Af
[
x
]; отражение графика относительно оси
абсцисс
(
этап
выполняется только приA<0);
4
.y=A·
f
(x); сжатие
или растяжение графика
вдоль оси ординат;
5. y=f
(x) отражение
графика относительно оси ординат
(
этап
выполняется только при<0);
6
.y=f
(
x); сжатие
или растяжение вдоль оси абсцисс;
7. y=f
( x);
Проводя
построение графика шаг за шагом в
порядке, обратном порядку упрощения
вида функции с учётом всех указанных
правил, получим график исходной функции.
Пример 17. Построить
график функции y=
.
Р
е ш е н и е: Схема построения графика :
y
=
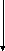
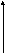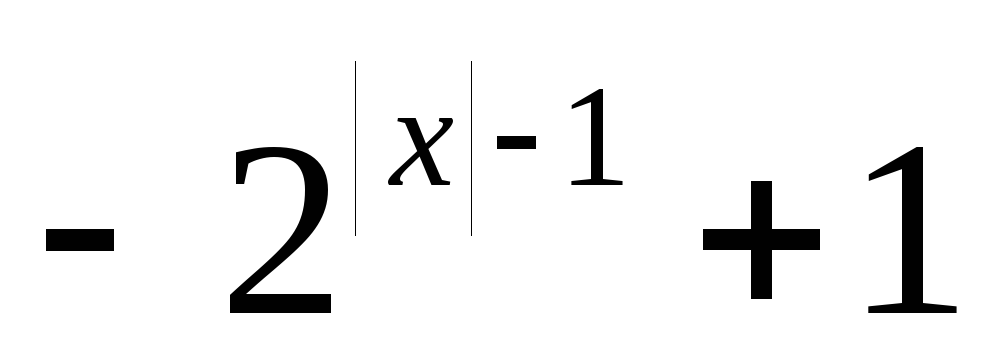
x
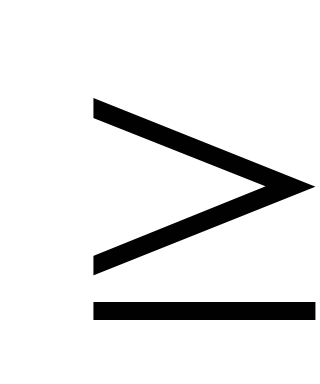0,
y=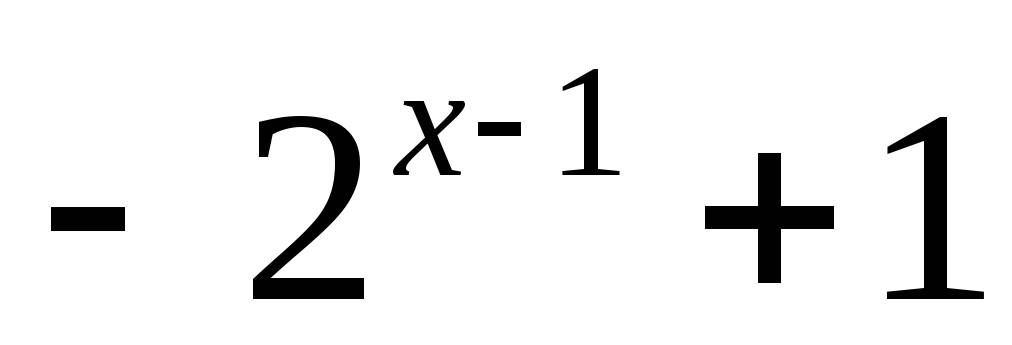
;y=
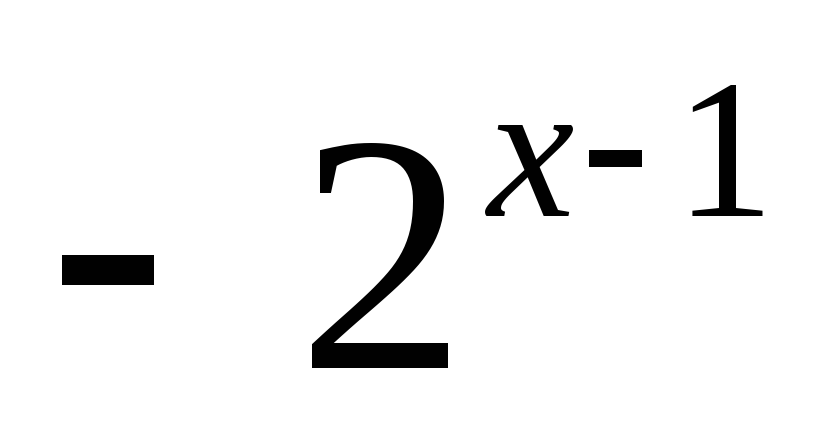;у=
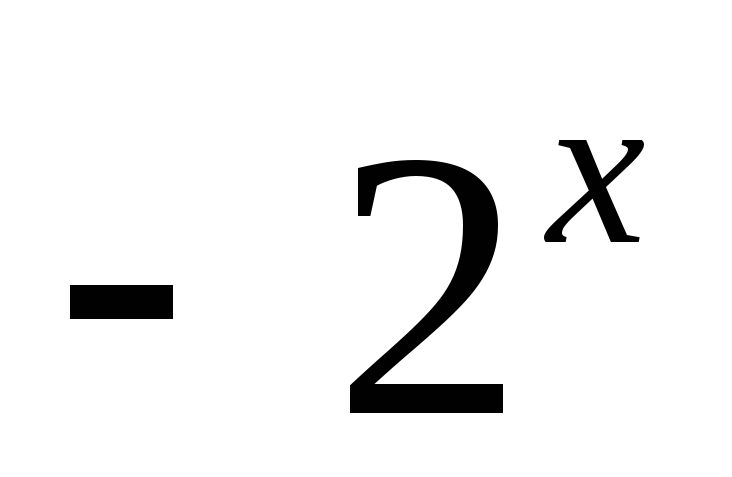;y=
;
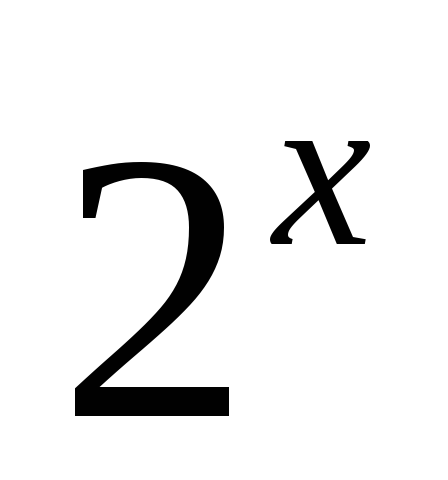Итак,
построение графика исходной функции
следует начинать с построения графика
функции y=
.
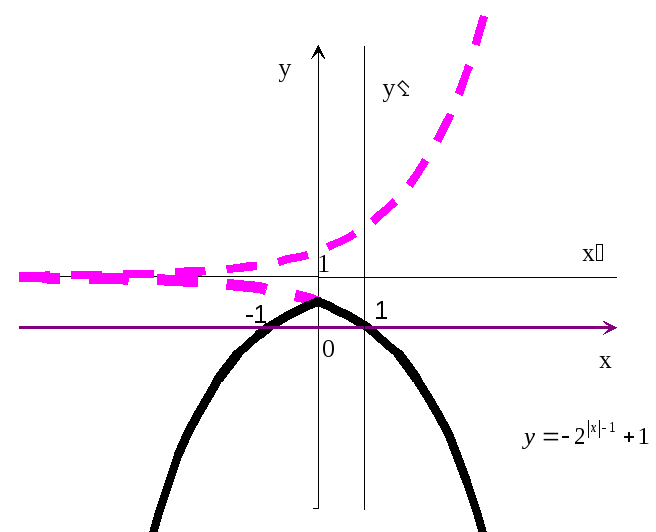
График (рис.20) пересекает ось ординат
в точке
(из условияx=0),
а ось абсцисс в точках x=1
(из условия y=0,
т.е.
=0).
В
заключении отметим, что порядок упрощения
целесообразно проводить в следующей
последовательности.
Использование
чётности или нечётности функции.Перенос осей.
Отражение и
деформация.
Построение
же графика, как обычно, выполняется в
обратной последовательности.
Рис.20
Задание для
самостоятельного выполнения
Ниже
приводятся тексты заданий для
самостоятельного выполнения. Вам
необходимо построить графики функций,
оформить работу отдельно от решений по
другим предметам и выслать в адрес
Хабаровской краевой заочной
физико-математической школы.
М.11.2.1 С
помощью элементарных преобразований
постройте графики следующих функций:
y=x2-2;
y=(x+1)2;
y=sin
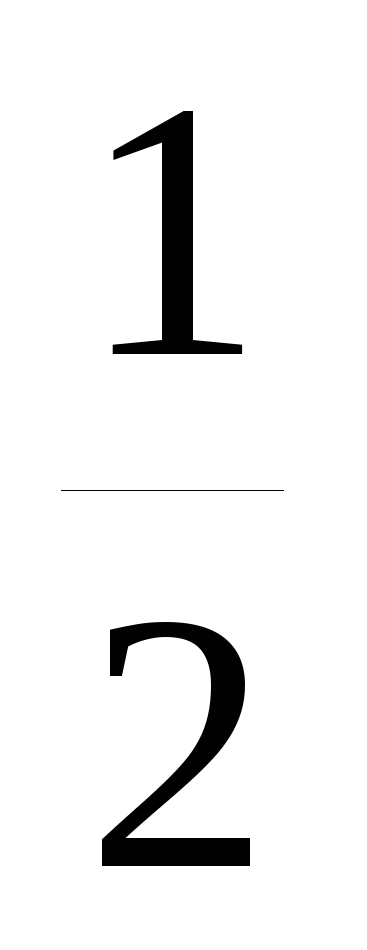x;y=-
3sin x;y=tg
;
М.11.2.2.
Написать последовательность преобразований
и построить графики следующих функций:
y=
;y=(x-1)3+2;
y=ln
(1-x);y=tg(-
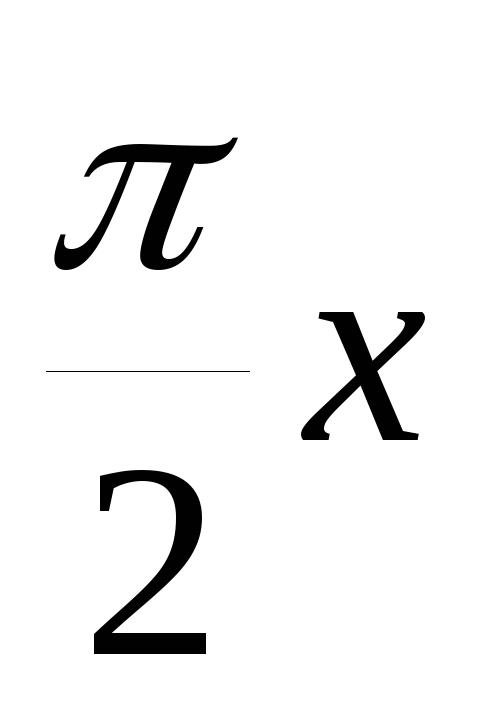);y=
cos(2x-1)-2.
Хабаровская краевая заочная
физико-математическая школа
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Если Вы знаете, как выглядят графики простейших элементарных функций, или умеете быстро строить их по характерным точкам, то сумеете также быстро построить на их основе графики более сложных функций того же класса. Для этого существуют правила преобразования графиков функций. Они легко запоминаются, но если Вы всё же не уверены в результате, проверьте его по одной-двум хорошим точкам. Эти правила, разумеется, общие для всех функций, а не только для тех, которые изучают в школе, поэтому известный график дальше будем называть заданным.
Пусть задан график функции y = f(x). Чтобы построить график функции
- y = mf(x), где m > 0 и m ≠ 1, нужно ординаты точек заданного графика умножить на m. Такое преобразование называется растяжением от оси x c коэффициентом m, если m > 1, и сжатием к оси x, если 0 < m < 1.
- y = −f(x) получается из графика функции f(x) преобразованием симметрии относительно оси x. (Преобразование симметрии — зеркальное отражение относительно прямой.)
- y = f(x) + n, получается из графика функции f(x) параллельным переносом последнего вдоль оси ординат на n единиц вверх, если n > 0 и, соответственно на |n| единиц вниз, если n
- y = f(kx), где k > 0 и k ≠ 1. Искомый график функции получается из заданного сжатием с коэффициентом k к оси y (если 0 < k < 1 указанное «сжатие» фактически является растяжением с коэффициентом 1/k)
- y = f(−x) получается из графика функции f(x) преобразованием симметрии относительно оси y
- y = f(x + l) получается из графика функции f(x) параллельным переносом последнего на l единиц влево, если l > 0 и, соответственно на |l| единиц вправо, если m < 0.
Например, пусть задан график функции y = √x_.
Чтобы построить графики других функций, содержащих аргумент (x) под знаком квадратного корня, воспользуемся перечисленными выше правилами. Заданный график повторим во вновь начерченных осях «карандашом бледно», требуемый график, который получится после преобразований, сделаем более интенсивным. В тетради лишнее можно будет удалить ластиком, останется только результат выполнения задания.
| Пример 1a. Построить график функции y = 2√x_
Растянули в 2 раза от оси x. Ордината каждой точки увеличилась в 2 раза. | Пример 1b. Построить график функции y = √x_ /2
Сжали вдвое к оси x. Ордината каждой точки уменьшилась в 2 раза. |
| Пример 3a. Построить график функции y = √x_ + 2
Параллельно перенесли на 2 единицы вверх вдоль оси y. Ордината каждой точки увеличилась на 2. | Пример 3b. Построить график функции y = √x_ − 2
Параллельно перенесли на 2 единицы вниз вдоль оси y. Ордината каждой точки уменьшилась на 2 единицы. |
| Пример 4a. Построить график функции y = √2x__
Сжали вдвое к оси y. Абсцисса каждой точки уменьшилась в 2 раза. | Пример 4b. Построить график функции y = √x/2___
Растянули в 2 раза от оси y. Абсцисса каждой точки увеличилась в 2 раза. |
| Пример 6a. Построить график функции y = √x + 2____
Параллельно перенесли на 2 единицы влево вдоль оси x. Абсцисса каждой точки уменьшилась на 2 единицы. | Пример 6b. Построить график функции y = √x − 2____
Параллельно перенесли на 2 единицы вправо вдоль оси x. Абсцисса каждой точки увеличилась на 2 единицы. |
| Пример 2. Построить график функции y = −√x_
Применили преобразование симметрии – зеркально отразили относительно оси x. | Пример 5. Построить график функции y = √−x__
Применили преобразование симметрии – зеркально отразили относительно оси y. |
Заметим, что параллельный перенос графика относительно одной из осей в какую-либо сторону равносилен переносу этой оси относительно графика в противоположную сторону. Поэтому 3-е и 6-е правила можно объединить следующим образом: чтобы построить график функции
y = f(x − m) + n
нужно выполнить параллельный перенос всей плоскости координат так, чтобы началом новой системы координат x‘y‘ была точка O‘(m;n). Очевидно, что вместо того, чтобы дважды перерисовывать график, проще перечертить оси.
Пример 7.
Задан график функции y = √x_. Построить график функции y = √x + 3____ − 1.
В этом случае m = −3, n = −1. Если есть затруднения в определении знаков m и n, то записывайте формулу функции так, чтобы она совпадала с правилом
y = f(x − m) + n; y = √x − m_____ + n; y = √x − (−3)_______ + (−1)
Построение выполняем так. Чертим оси нужной системы координат. Находим точку с координатами (−3;−1). Проводим через неё «бледно карандашом» прямые параллельные основным осям. Это вспомогательная система координат. В этой (карандашной) системе координат строим график y = √x_. Относительно основной системы координат, он является графиком функции y = √x + 3____ − 1. Т.е., если карандаш удалить ластиком, то останется график, который требовалось построить.
Если нужно скомбинировать только параллельные переносы, чтобы построить график функции, то всё равно в каком порядке их выполнять, и всё равно, что переносить — оси или кривые. Но если нужно построить график сложной функции, используя и перенос, и растяжение-сжатие, и отражения, то следует тщательно соблюдать порядок выполнения операций.
Последовательность преобразований при построении графиков.
Пусть задан график функции y = f(x) и нужно построить график функции y = m·f(kx + l) + n, где k, l, m, n — числа.
- Записываем формулу функции в виде
y = m·f(k·(x + l/k)), т.е. выносим за скобки коэффициент при х в аргументе функции. - Производим сжатие с коэффициентом k вдоль оси Ох к оси Oy. (Если k Oy.)
- Если k Oy.
- Осуществляем параллельный перенос (сдвиг) полученного графика на l/k единиц влево или вправо (в зависимости от знака, для положительного числа влево).
- Производим растяжение с коэффициентом m от оси Oх (вдоль оси Оy). (Если m Ox.)
- Если m Ox.
- Осуществляем параллельный перенос (сдвиг) полученного графика на n единиц вверх или вниз (в зависимости от знака, при n >0 вверх).
Пример 8.
Задан график функции y = √x_. Построить график функции y = −0,5√3x − 12______ + 2.
1. Записываем формулу функции в виде y = −0,5·√3·(x − 4)_______ + 2,
т.е. выносим за скобки коэффициент при х под знаком квадратного корня с учетом того, что 12/3 = 4.
2. Строим известный график функции. ——
3. Производим сжатие в 3 раза к оси Oy. ——
4. — (преобразование симметрии относительно оси Oy не требуется, т.к. k = 3 > 0).
5. Сдвигаем полученный график на 4 единицы вправо. ——
6. Производим сжатие в 2 раза (растяжение с коэффициентом 0,5) к оси Oх. ——
7. Симметрично отражаем график относительно оси Ox. ——
8. Сдвигаем последний на 2 единицы вверх. Получили требуемый график. ——
Проверим результат по «удобным» точкам. Например, x1 = 4 и x2 = 16.
y1 = −0,5√3·4 − 12_____ + 2 = 2.
y2 = −0,5√3·16 − 12_____ + 2 = −1.
Точки с координатами (4;2) и (16;−1) действительно принадлежат последнему графику.
Источник