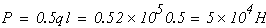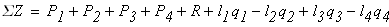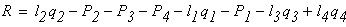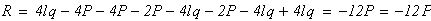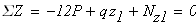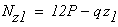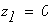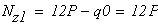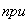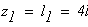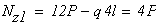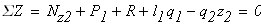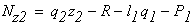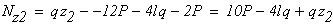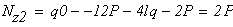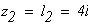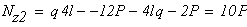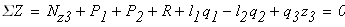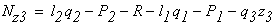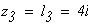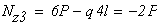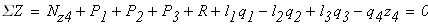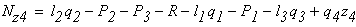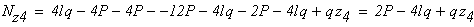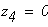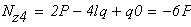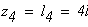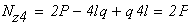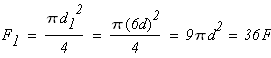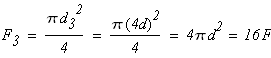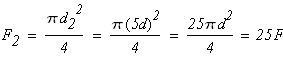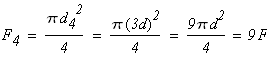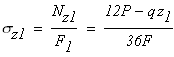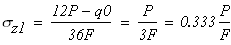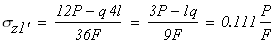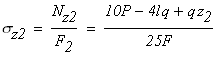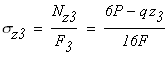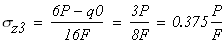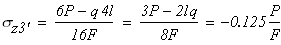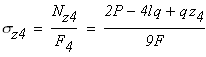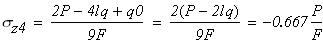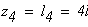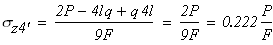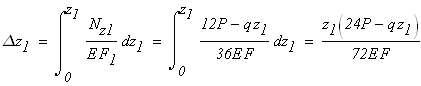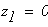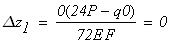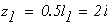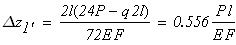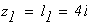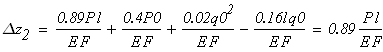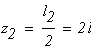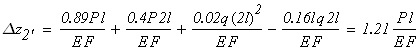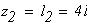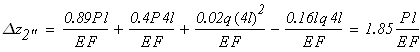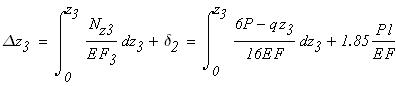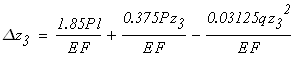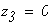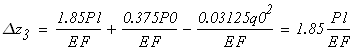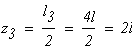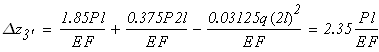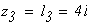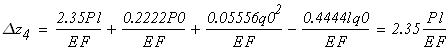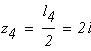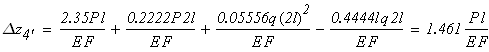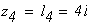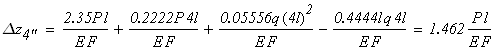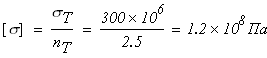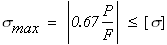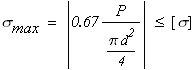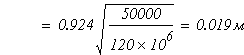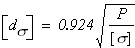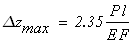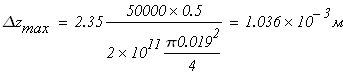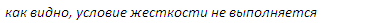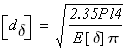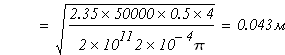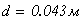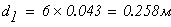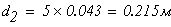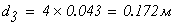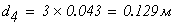Расчет ступенчатого стержня на прочность при растяжении и сжатии
Сопромат → растяжение — сжатие стержня расчет онлайн
Артикул: sopr0002
Автор решения: admin
Расчет на прочность и жесткость стержня при растяжении сжатии.
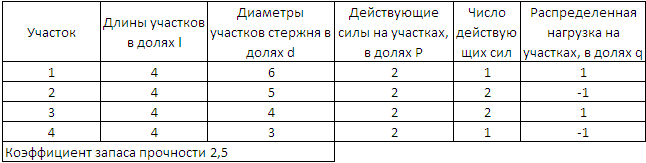
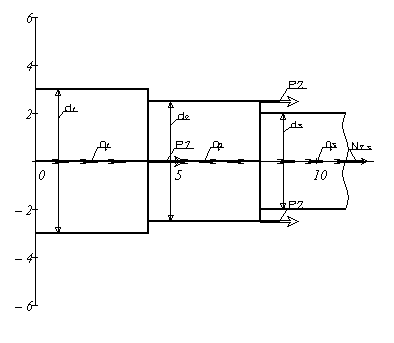
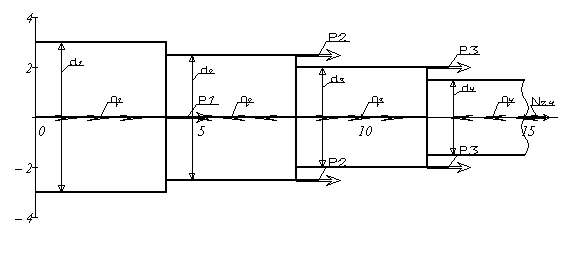
Задан ступенчатый стержень, нагруженный внешними сосредоточенными силами P и распределенными нагрузками q.
Необходимо для ступенчатого стержня выполнить следующее:
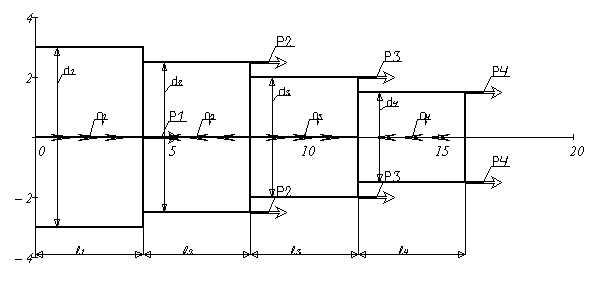
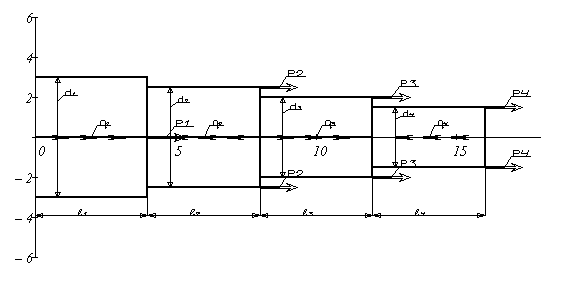
1. Начертить индивидуальную расчетную схему стержня.
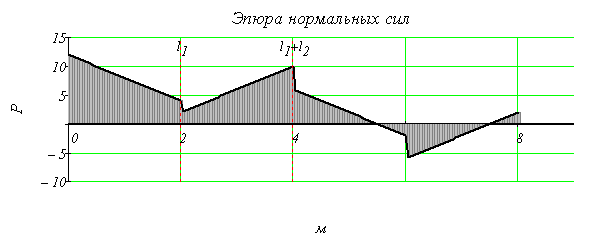
2. Построить эпюру нормальных сил.
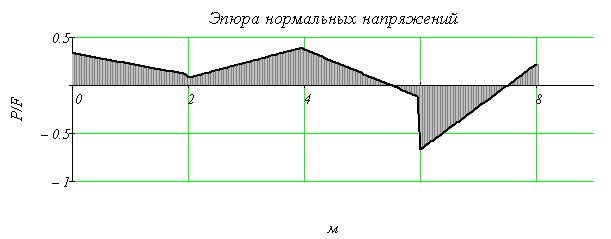
3. Построить эпюру нормальных напряжений
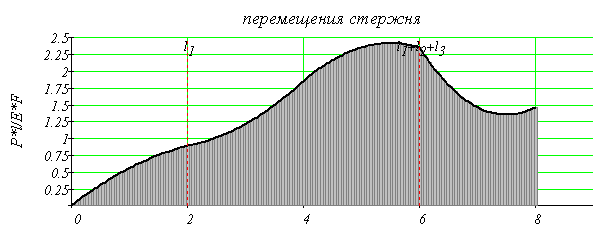
4. Построить эпюру перемещений.
5. Найти диаметры поперечных сечений участков стержняиз условия прочности при заданном коэффициенте запаса прочности.
6. Проверить и при необходимости обеспечить выполнение условия жесткости стержня.
Важно!
Если ваша задача из задачника Добровольского или Девятерикова (Исходная таблица.), то для заказа следует нажать «Добавить в корзину» и в окне оплаты в комментариях указать свой 4-х значный вариант. Либо написать мне |через сайт| в контакте| на почту|
Если у вас значения для расчета произвольные — нажимайте «заказать подобную задачу» и в окне заказа указывайте свои расчетные данные. Либо высылайте файл с заданием.
Вернуться в каталог
Заказать похожую задачу
Часть готового решения
Задан ступенчатый стержень, нагруженный внешними сосредоточенными силами P и распределенными нагрузками q.
Необходимо для ступенчатого стержня выполнить следующее:
1. Начертить индивидуальную расчетную схему стержня.
2. Построить эпюру нормальных сил.
3. Построить эпюру нормальных напряжений
4. Построить эпюру перемещений.
5. Найти диаметры поперечных сечений участков стержняиз условия прочности при заданном коэффициенте запаса прочности.
6. Проверить и при необходимости обеспечить выполнение условия жесткости стержня.
При расчетах принять:
распределенная нагрузка 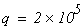
длина 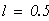
Сила
Модуль упругости стержня при растяжении (сжатии) 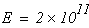
Предел текучести материала стержня 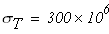
Допускаемое перемещение 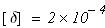
Решение: Вычерчиваем индивидуальную расчетную схему стержня, в соответствии с иходными данными.
Определяем реакцию опоры из условия статичтического равновесия стержня
откуда получаем
Используя метод сечений, определяем законы изменения нормальной силы на участках стержня.
Первый участок
при
Второй учаток
при
при
третий участок
при
при
четвертый участок
при
при
По полученным значениям 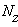
Обозначаем площадь поперечного сечения стержня диаметром d через 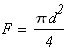
Вычисляем нормальные напряжения, действующие в поперечных сечениях, на участках стержня
Первый участок:
при
при
Второй участок:
при
при
Третий участок:
при
при
Четвертый участок
при
при
Используя закон Р. Гука в интегральной форме, находим перемещения на участках стержня.
Первый участок
при
при
при
Второй участок
при
при
при
Третий участок
при
при
Четвертый участок
при
при
при
Вычисляем допускаемое нормальное напряжение
Из условия прочности при растяжении (сжатии) стержня
вычисляем допускаемый диаметр
Проверяем выполнение условия жесткости стержня
с учетом того, что
допустимый диаметр стержня из условия жесткости стержня
Окончательно выбираем диаметр
Таким образом, окончательно принимаем:
При этих значениях поперечных размеров будет обеспечена как прочность так и жесткость стержня
Заказать похожую задачу
Источник
Содержание
| Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие.……………………………………………………………………3 |
| Задача № 2 Расчет оптимального сечения ступенчатого стержня при деформации растяжение и сжатие……………………………………………..8 |
| Задача № 3 Расчет статически определимой стержневой системы, работающей на растяжение и сжатие………………………………………….12 |
| Задача № 4 Расчет вала на прочность и жесткость……………………………15 |
| Задача № 5 Расчет балки на прочность при плоском изгибе…………………20 |
| Задача №6 Расчет балки на прочность при плоском изгибе…………………23 |
| Задача № 7 Сравнение прочности балок различных сечений……………….27 |
| Задача № 8 Расчет сжатого стержня на устойчивость……………………….29 |
| Список литературы………………………………………………………………33 |
Задача № 2 Расчет оптимального сечения ступенчатого стержня при деформации растяжение и сжатие.
Задание:Определить оптимальный диаметр сечения круглого стержня на каждом участке по условию прочности. Определить продольные деформации, возникающие на каждом участке стержня. Стержень изготовлен из стали:
Е = 2*105 МПа; σТ = 240 МПа. Допускаемый коэффициент запаса статической прочности [n] выбрать самостоятельно ([n]= 1,2…1,8). Весом стержня пренебречь. Схема стержня приведена на рис. 2.
Исходные данные:F1=17 кН; F2=28 кН; F3=7кН; l1=130 см=1,3 м;
l2=140 см=1,4 м; l3=65 см=0,65 м.
Решение:Для определения продольной силы используем метод сечений.
Эпюру продольных сил необходимо строим, руководствуясь правилом: продольная сила в любом сечении стержня равна алгебраической сумме проекций всех внешних сил, расположенных по одну сторону от сечения на ось стержня. Продольная сила считается положительной, если она соответствует деформации растяжения (направлена от сечения) и отрицательной, если она вызывает сжатие (направлена к сечению).
1.Разобьем стержень на отдельные участки, начиная от свободного конца. Границы участков определяются точками приложения внешних сил. Всего по длине стержня в данной задаче будет три участка. Проведя сечения и отбрасывая левые части стержня, можно определить продольные силы в его поперечных сечениях без вычисления опорных реакций в заделке.
1 участок (сечение 1-1) : NI = -F3 = -7 кН.
на первом участке осуществляется деформация сжатия.
2 участок (сечение 2-2): N2 = -F3 +F2 = -7+28=21 кН.
на втором участке осуществляется деформация растяжения.
3 участок (сечение 3-3) N3 =-F3 +F2+F1 = -7+28+17=38 кН.
на третьем участке осуществляется деформация растяжения.
Таким образом, в заделке действует реакция равная N3 =38кН.
Эпюра продольных сил показана на рис.1. Эпюру продольных сил строим в масштабе = .
2. Допускаемое напряжение вычисляем по формуле: .
Допускаемые напряжения при сжатии и растяжении для пластичного материала, при условии, что коэффициент запаса n=1,8.
=240/1,8=133,3Мпа
3. Требуемая площадь сечения определяется из формулы условия прочности на растяжения.
Þ
Площадь круглого сечения А=
1 участок:
Принимаем d1=0,09м, А1=
2 участок:
Принимаем d2=0,015 м, А2=
3 участок:
Принимаем d1=0,02м, А3=
Удлинения (укорочения) части стержня определяем по формуле ,где – соответственно длина участка, внутреннее усилие, площадь поперечного сечения, Е–модуль упругости материала.
Укорочение 1 участка .
Удлинение 2 участка
Удлинение 3 участка .
В правом конце стержня заделка, перемещение в этом конце отсутствует. Поэтому построение эпюры смещения стержня необходимо строить, начиная с левого конца.
На третьем участке смещение изменяется от нуля до =7,87*10-4 м;
на втором участке: от =7,87*10-4м до
=16,17*10-4 м;
на первом участке: от 16,17*10-4 м
до 7,87*10-4 +8,3*10-4 -3,55*10-4=12,62*10-4 м.
Эпюры смещения строим в масштабе:
= .
Ответ: Полное удлинение стержня составило 12,62*10-4м.
Задача № 3 Расчет статически определимой стержневой системы,
Задача № 4 Расчет вала на прочность и жесткость.
Задание:Определить диаметры ступенчатого вала из условия прочности и жесткости на кручение. Определить угол закручивания вала.
Вал изготовлен из стали: [Θ] = 1,75 *10-2 рад/м, G = 8 *1010 Па
Схема вала приведена на рис. 4.
Исходные данные: а=1,4м; b=0,6м, c=0,6м, М1 =360Н*м; М2 = 400Н*м;
М3 = 400Н*м; М4 = 500Н*м; [t] = 55 Мпа.
Решение.
1. Определение внутренних крутящих моментов по участкам.
Для определения знака крутящего момента примем следующее правило: если смотреть на отсеченную часть бруса со стороны внешней нормали к сечению, то момент сечении будет положителен в том случае, когда сумма внешних скручивавших моментов поворачивает отсеченную часть бруса по часовой стрелке, и отрицателен при повороте части бруса в противоположном направлении.
Неизвестный момент М5 в заделке найдем из уравнения равновесия для всего вала. Условно примем направление момента М5 за отрицательное. Тогда уравнение равновесия принимает вид
-М1 +М2 +М3 -М4-М5 = 0
Из решения этого уравнения получим
М5 =-М1 +М2 +М3 -М4=-360+400+400-500= -60Н*м.
Для построения эпюры крутящих моментов применяем метод сечений к каждому участку вала в отдельности (следует заметить, что построение эпюры крутящих моментов совершенно аналогично построению эпюры продольных сил). Крутящие моменты в сечениях определяются как алгебраические суммы внешних моментов, приложенных по одну сторону от сечения.
Определим крутящие моменты на каждом участке, проведя последовательно
сечения на четырехучастках вала и рассмотрим равновесие соответствующих
оставшихся правых частей.
В сечении 1-1: .
В сечении 2-2: .
В сечении 3-3:
В сечении 4-4:
По полученным данным строим эпюру крутящих моментов, откладывая по вертикальной оси значения моментов. Отрицательные моменты откладываем вниз по осевой линии (рис. 4). Эпюру моментов строим в масштабе = .
2. По найденным значениям крутящих моментов из расчетов на прочность и жесткость в каждом сечении определим диаметры валов.
Расчет на прочность ведется по допускаемому напряжению при кручении
где –крутящий момент, действующий в сечении бруса;
–полярный момент сопротивления для круглого сечения, –диаметр вала. Из формулы выразим диаметр
По формуле определим диаметры для всех сечений.
Сечение 1-1: 0,0359м, принимаем d1=0,036м.
Сечение 2-2: 0,021м, принимаем d2=0,022м.
Сечение 3-3: 0,0303м, принимаем d1=0,032м.
Сечение 4-4: 0,0177м, принимаем d4=0,018м.
3. Расчет на жесткость ведется по допускаемому относительному углу закручиванию , где –полярный момент сопротивления круглого сечения.
В соответствии с формулой определим диаметр вала из условия жесткости
По формуле определим диаметры для всех участков.
Сечение 1-1: 0,0437м, принимаем d1=0,045м.
Сечение 2-2: 0,0292м, принимаем d2=0,03м.
Сечение 3-3: 0,0384м, принимаем d1=0,04м.
Сечение 4-4: 0,0257м, принимаем d4=0,026м.
4. В соответствии с расчетами на прочность и жесткость выбираем наибольшее значение диаметров для каждого участка. В результате получим следующие значения:
5. Абсолютные углы закручивания для каждого участка можно определить по формуле , где – длина участка.
Полярные моменты инерции для каждого сечения
Сечение 1-1: м4;
Сечение 2-2: м4.
Сечение 3-3: м4;
Сечение 4-4: м4.
Далее определим углы закручивания.
= -0,0218 рад – угол поворота сечения В относительно сечения А (или угол закручивания участка АВ).
= -0,0095 рад – угол поворота сечения С относительно сечения В (или угол закручивания участка ВС).
= 0,009 рад – угол поворота сечения D относительно сечения C (или угол закручивания участка CD).
=- 0,0233 рад – угол поворота сечения Е относительно сечения D (или угол закручивания участка DЕ).
Строим эпюру углов закручивания для всего вала (рис. 4). За начало координат выбран крайний левый конец бруса (сечение D). В пределах каждого из участков бруса эпюра линейна, поэтому достаточно знать углы поворота только для граничных сечений участков.
В сечении от Е до D полный угол закручивания вала равен
-0,0233 рад;
В сечении от Е до С полный угол закручивания вала равен
-0,0233+0,009=-0,0143 рад;
В сечении от Е до В полный угол закручивания вала равен
— 0,0233+0,009-0,0095=-0,0238 рад;
В сечении от Е до А полный угол закручивания вала равен
— 0,0233+0,009-0,0095-0,0218=-0,0456рад.
Ординаты этой эпюры дают значения углов поворота соответствующих поперечных сечений вала.
Эпюру углов поворота строим в масштабе
= .
Ответ: и полный угол закручивания -0,0456 рад.
Список литературы
1. Сопротивление материалов: учебное пособие для вузов/ Н.Н.Вассерман и др. — Пермь: Изд-ва ПНИПУ, 2011 – 364 с.
2. Прикладная механика: Учеб. Для вузов/ В.В.Джамай, Ю.Н.Дроздов, Е.А.Самойлов и др. – М. Дрофа, 2004. – 414 с.
3. Феодосьев В.И. Сопротивление материалов. М.: МГТУ им. Н.Э. Баумана, 1999 – 592 с.
Содержание
| Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие.……………………………………………………………………3 |
| Задача № 2 Расчет оптимального сечения ступенчатого стержня при деформации растяжение и сжатие……………………………………………..8 |
| Задача № 3 Расчет статически определимой стержневой системы, работающей на растяжение и сжатие………………………………………….12 |
| Задача № 4 Расчет вала на прочность и жесткость……………………………15 |
| Задача № 5 Расчет балки на прочность при плоском изгибе…………………20 |
| Задача №6 Расчет балки на прочность при плоском изгибе…………………23 |
| Задача № 7 Сравнение прочности балок различных сечений……………….27 |
| Задача № 8 Расчет сжатого стержня на устойчивость……………………….29 |
| Список литературы………………………………………………………………33 |
Задача № 1 Проверка прочности ступенчатого стержня при деформации растяжение и сжатие.
Задание:Оценить прочность ступенчатого стержня из хрупкого материала. Определить его деформацию. Стержень изготовлен из чугуна: Е = 1,2*105 МПа; σвр= 113 МПа; σвсж= 490 МПа. Допускаемый коэффициент запаса статической прочности [n] выбрать самостоятельно (в данной задаче принимаем [n]= 1,2…1,8). Весом стержня пренебречь.
Схема стержня приведена на рис. 1.
Исходные данные: l1=0,5м; l2=0,2м; l3=0,4м; А=4*10-4м2; А1=А=
=4*10-4м2; А2=3А=12*10-4м2; А3=1,5А=6*10-4м2; F1=30кН; F2=60кН; F3=20кН.
Решение. Разобьем стержень на отдельные участки, начиная от свободного конца. Границы участков определяются точками приложения внешних сил или местами изменения размеров поперечного сечения. Всего по длине стержня в данной задаче будет три участка. Проведя сечения и отбрасывая левые части стержня, можно определить продольные силы в его поперечных сечениях без вычисления опорных реакций в заделке.
Для того, чтобы определить усилие NI, проводим сечения в пределах первого участка. Рассмотрим равновесие оставшейся правой части стержня.
Из уравнения равновесия оставшейся правой части выразим внутреннюю продольную силу NIчерез внешние силы, приложенные к оставленной части
NI =- F1 = -30 кН
Так как положительное направление совпадает с деформацией растяжения, то знак минус означает, что на первом участке осуществляется деформация сжатия.
Аналогично находим внутреннее усилие NII, действующее на втором
участке. Для этого проводим произвольное сечение на втором участке и рассматриваем равновесие оставшейся правой части стержня .
Уравнение равновесия в проекции на ось стержня для второго участка
-F1 + F2 -NII = 0
Решая это уравнение, получим
NII = -F1 -F2 = -30+60 = 30 кН.
на втором участке осуществляется деформация растяжения.
Для того, чтобы определить внутреннее усилие NIII, действующее на третьем участке рассмотрим равновесие оставшейся части стержня.
-F1 +F2 + F3 – NIII = 0.
Решая это уравнение, получим
NIII =-F1 + F2 +F3 = -30+60 +20=50 кН.
Таким образом, в заделке действует реакция равная NIII =50 кН.
на третьем участке осуществляется деформация растяжения.
Эпюра продольных сил показана на рис.1. Эпюру продольных сил строим в масштабе =
Чтобы определить напряжение в поперечных сечениях бруса, нужно разделить числовые значения продольных сил на площади этих сечений.
Для первого участка
.
Допускаемые напряжения при сжатии, при условии, что коэффициент запаса n=1,2
=490/1,2=408 Мпа.
Условие прочности для первого участка выполняется .
Недогруз конструкции на первом участке составил
*100%= = 81,7%, что выше допустимого (10%).
Для сечения 2-2: .
На втором участке деформация растяжения. Допускаемые напряжения при растяжении, при условии, что коэффициент запаса n=1,2
=113/1,2=94,2 Мпа.
Условие прочности для первого участка выполняется .
Недогруз конструкции на втором участке составил
*100%= = 73,4%, что выше допустимого (10%).
Для сечения 3-3: .
На третьем участке деформация растяжения. Допускаемые напряжения при растяжении =94,2 Мпа.
Условие прочности для третьего участка выполняется .
Недогруз конструкции на третьем участке составил
*100%= =11,6 %, что выше допустимого (10%).
Эпюра нормальных напряжений по длине бруса показана на рис. 1.
Эпюры нормальных напряжений строим в масштабе:
= .
укорочение участков бруса определяются по формуле
,
где – соответственно длина участка, внутреннее усилие, площадь поперечного сечения, напряжение в сечении. Е–модуль упругости материала.
укорочение первого участка
.
удлинение второго участка
удлинение третьего участка
.
В левом конце стержня заделка, перемещение в этом конце отсутствует. Поэтому построение эпюры деформации стержня необходимо строить, начиная с левого конца.
На третьем участке деформация изменяется от нуля до =27,78*10-5м;
на втором от =27,78*10-5м
до =31,95*10-5м;
на первом от 31,95*10-5м
до 27,78*10-5 +4,17*10-5-31,25*10-5=0,7*10-5м.
Эпюры смещения строим в масштабе:
= .
Ответ: Полное удлинение бруса составило 0,7*10-5м и прочность стержня по допускаемым напряжениям выполняется.
Источник
Геометрических характеристик плоских сечений
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
Методические указания
к выполнению контрольной работы 1
по курсу «Сопротивление материалов» для студентов
специальностей 151001.65, 240801.65, 260601.65
Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета
Саратов 2009
ОБЩИЕ ПОЛОЖЕНИЯ
В элементах конструкций при действии внешних сил возникают внутренние силы упругости. При осевом растяжении (сжатии) стержня в его сечениях возникают только продольные силы N. Для их вычисления применяется метод сечений. Растягивающие продольные силы принято считать положительными, а сжимающие – отрицательными. Мерой внутренних сил является напряжение, оно характеризует интенсивность внутренних сил в точках сечения. При осевом растяжении (сжатии) стержня в его поперечных сечениях действуют только нормальные напряжения s. Знак s определяется знаком N. При растяжении стержня его длина увеличивается, а поперечные размеры уменьшаются. При сжатии – наоборот. В результате изменения длины стержня его сечения совершают линейные перемещения d вдоль продольной оси Z.
В задаче 1 проводится вычисление продольных усилий, нормальных напряжений в поперечных сечениях стержня, определение перемещений сечений стержня, а также построение соответствующих эпюр. Так как основной задачей расчета конструкции является обеспечение ее прочности в условиях эксплуатации, то также определяется коэффициент запаса прочности.
Стержни и стержневые системы, в которых внутренние усилия могут быть определены при помощи уравнений равновесия статики, называются статически определимыми. Стержни и системы, внутренние усилия в которых нельзя определить при помощи одних лишь уравнений статики, называются статически неопределимыми. Для их расчета необходимо рассмотреть систему в деформированном состоянии и составить дополнительные уравнения, связывающие перемещения элементов системы, Раскрытие статической неопределимости системы показано в задаче 2.
При центральном растяжении-сжатии и при чистом сдвиге прочность и жесткость стержня зависит от простейшей геометрической характеристики – площади поперечного сечения А. При других видах деформации, например, кручение и изгиб, прочность и жесткость стержня определяются не только площадью поперечного сечения стержня, но и формой сечения. Поэтому для расчета на прочность и жесткость в этих случаях приходится использовать более сложные геометрические характеристики сечений: статические моменты – Sx и Sy; моменты инерции: осевые Jx и Jy, центробежный Jxy, полярный Jp; моменты сопротивления: осевые Wx и Wy, полярный Wp. В задаче 3 определяются геометрические характеристики плоского сечения стержня, состоящего из двух прокатных профилей.
РАСЧЕТ СТУПЕНЧАТОГО БРУСА НА РАСТЯЖЕНИЕ–СЖАТИЕ
Для ступенчатого стального бруса (рис. 1, а), выполненного из стали марки Ст. 3, имеющей предел текучести sТ = 240 МПа, модуль Юнга
E = 2×105 MПа, требуется:
1. Построить по длине бруса эпюры продольных сил N, нормальных напряжений s и перемещений поперечных сечений d.
2. Вычислить коэффициент запаса прочности бруса n.
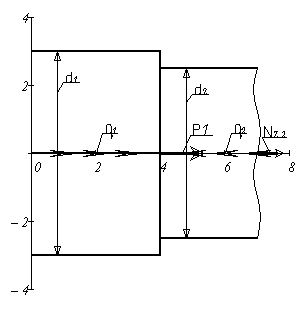
Проведем ось z, совпадающую с осью бруса. Направление оси выбираем произвольно. Брус жестко защемлен верхним концом в опоре, в которой возникает опорная реакция R. Направление вектора реакции выбираем произвольно. Величину опорной реакции найдем из уравнения равновесия статики:
∑ FZ = 0; R – F1 + F2 = 0; R = F1 — F2 == 24 кН.
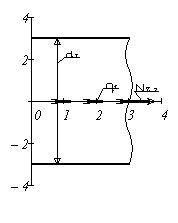
Разделим брус на силовые участки. Границами участков являются поперечные сечения бруса, проходящие через точки приложения внешних нагрузок и сечения, в которых изменяется площадь поперечного сечения бруса. Точки пересечения оси бруса и граничных сечений обозначим буквами B, C, D, K. Получим 3 участка бруса.
Используем метод сечений. На каждом участке проводим сечения I-I,
II-II, III-III. При этом одну из частей бруса (более сложную) мысленно отбрасываем и к плоскости сечения оставшейся части бруса прикладываем вектор продольной силы N в направлении внешней нормали к сечению. Рассматриваем равновесие оставшейся части бруса (рис. 2).
Уравнения равновесия статики на каждом участке запишутся:
на первом участке BC (рис. 2, а) ∑ FZ = 0; R – N1 = 0; N1 = R = 24 кН;
на втором участке CD (рис. 2, б) ∑ FZ = 0; R – N2 = 0; N2 = R = 24 кН;
на третьем участке DK (рис. 2, в) ∑ FZ = 0; N3 + F2 = 0; N3 = — F2 = — 42 кН.
Проведем вертикальную линию (рис. 1, б), параллельную оси y и отложим от нее в выбранном масштабе на каждом участке вдоль этой линии положительные значения продольной силы вправо, а отрицательные влево. Получим эпюру продольных сил N (рис. 1, б).
Определим нормальные напряжения σ, МПа, на каждом участке бруса по формуле
где N, Н – продольная сила на данном участке; А, м2 – площадь поперечного сечения данного участка.
На первом участке BC
На втором участке CD
На третьем участке DK
Проведем вертикальную линию (рис. 1, в), параллельную оси y и отложим в выбранном масштабе на каждом участке вдоль этой линии положительные значения нормальных напряжений вправо, а отрицательные влево. Получим эпюру нормальных напряжений σ.
Найдем удлинения ∆ℓ, м, участков бруса по формуле
,
где N, Н – продольная сила на данном участке; ℓ, м — длина данного участка; Е, МПа – модуль Юнга материала бруса на данном участке; А, см2 – площадь поперечного сечения данного участка.
На первом участке ВС
.
На втором участке CD
.
На третьем участке DK
.
Определим перемещения сечений бруса, проходящих через границы участков. Перемещение сечения, проходящего через точку В равно нулю, так как в жесткой заделке нет перемещений, т. е. δВ = 0.
Между точками B и C находится первый участок. Перемещение сечения C будет равно δC = δВ + ∆ℓ1 = 0 + 0,72 · 10-4 = 0,72 · 10-4 м.
Между точками C и D находится второй участок. Перемещение сечения D будет равно δD = δC + ∆ℓ2 = 0,72 · 10-4 + 0,8 · 10-4 = 1,52 · 10-4 м.
Между точками D и K находится третий участок. Перемещение сечения D будет равно δK = δD + ∆ℓ3 = 1,52 · 1,8 · 10-4 = -1,28 · 10-4 м.
Отложим в выбранном масштабе на граничных сечениях положительные значения перемещений сечений вправо, а отрицательные влево. Получим эпюру перемещений сечений бруса δ (рис. 1, г).
Найдем коэффициент запаса прочности бруса по формуле
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ
СТЕРЖНЕВОЙ СИСТЕМЫ
Абсолютно жесткий брус (рис. 3) закреплен с помощью шарнирно-неподвижной опоры и двух стержней и нагружен силой Q. Требуется:
1. найти усилия и напряжения в стержнях, выразив их через силу Q;
2. из расчета по допускаемым напряжениям найти допускаемую нагрузку [Q], приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа;
3. из расчета по допускаемым нагрузкам найти предельную грузоподъемность системы и допускаемую нагрузку QДОП, если предел текучести σТ = 240 МПа и запас прочности n = 1,5;
4. сравнить величины [Q] и QДОП, полученные при расчете по допускаемым напряжениям и допускаемым нагрузкам.
Рис. 4 Рис. 5
(1)
Составлять уравнения и не имеет смысла, так как в них войдут не интересующие нас реакции опоры О (R3, R4). Таким образом, мы убеждаемся еще раз, что задача статически неопределима (в единственное уравнение статики (1) входят две неизвестные силы N1 и N2; нагрузку Q в этом уравнении считаем заданной).
Для составления дополнительного уравнения рассмотрим деформацию системы. Под действием нагрузки Q абсолютно жесткий брус CD, оставаясь прямым, повернется вокруг шарнира О и займет положение C1D1 (рис.6). Точка В опишет дугу, которую вследствие малости угла С1ОС заменим хордой ВВ1. Величина ВВ1 представляет собой удлинение второго стержня = ВВ1. Так как упругие деформации малы по сравнению с длинами стержней, то считают, что угол между абсолютно жестким брусом CD и ВК не изменился, то есть . Из рис. 3 следует, что a = 45°. При этом стержни 1 и 2 удлиняются соответственно на величины и .
Рис. 6
Удлинение стержня 1 () получаем на чертеже, опустив перпендикуляр ВМ из точки В на КВ1 (положение стержня 1 после деформации).
Из прямоугольного треугольника ВВ1М (рис.6) следует, что
(2)
На основании закона Гука (отрезок МВ1) и (отрезок ВВ1). При составлении этих выражений следует соблюдать соответствие направления нормальных сил N1 и N2 деформациям стержней 1 и 2. В данном случае стержни 1 и 2 растягиваются и силы N1 и N2 – растягивающие.
Условие совместности деформаций (2) перепишется так
(3)
Из рис. 3 видно, что — длина стержня 1; ℓ 2 = в – длина стержня 2. Тогда выражение (3) получает вид
(4)
Так как a = 45°, то получаем: N1 = N2. Решая совместно уравнения (1) и (4), получаем
N1 = N2 = 0,488 · Q.
После определения усилий N1 и N2 находим величины нормальных напряжений s1 и s2 в стержнях 1 и 2:
Определим допускаемую силу [Q]. из расчета по допускаемым напряжениям. Так как s2 > s1, то состояние второго стержня более опасно. Поэтому для определения допускаемой силы [Q]. следует приравнять напряжение во втором стержне s2 допускаемому напряжению [s] = 160 МПа.
(кН/м2)
244 [Q]. = 160 · 103 ; [Q]. = кН.
Допускаемая нагрузка [Q]. = 655,74 кН.
Определим допускаемую силу QДОП. из расчета по допускаемым нагрузкам. Напряжение во втором стержне оказалось больше, чем в первом, то есть s2 > s1. При увеличении силы Q напряжение во втором стержне достигнет предела текучести раньше, чем в первом. Когда это произойдет,