Расчет на внецентренное растяжение и сжатие примеры

Многие элементы строительных конструкций (колонны, стойки, опоры) находятся под воздействием сжимающих сил, приложенных не в центре тяжести сечения. Рассмотрим, например, колонну, на которую опирается балка перекрытия (рис. 11.11). Поскольку сила Р, характеризующая передачу нагрузки от балки на колонну, действует по отношению к ее оси с эксцентриситетом е, колонна испытывает сжатие с изгибом. При этом в поперечных сечениях колонны наряду с продольной силой N = —Р возникает изгибающий момент, величина которого равна М = Ре.
Таким образом, внецентренное растяжение и сжатие стержня имеют место в случае, когда нагрузки действуют вдоль прямой, параллельной оси стержня. Будем рассматривать в основном задачи внецентренного сжатия, наиболее характерные для элементов строительных конструкций. При внецентренном растяжении во всех приводимых ниже формулах надо изменить знак перед силой Р на противоположный.
Рассмотрим стержень, нагруженный на торце внецентренно приложенной в точке К сжимающей силой Р, направленной параллельно оси Ох (рис. 11.12, а). Обозначим координаты точки приложения силы через ур и zp- Перенесем силу в центр тяжести сечения и согласно правилам статики добавим два момента Mz=—Pyp и Му = —Pzp (рис. 11.12, б). При этом внутренние усилия в произвольном поперечном сечении стержня будут равны:


Рис. 11.11

Рис. 11.12
Согласно принятому правилу знаков внутренние усилия являются отрицательными, поскольку в точках первой четверти сечения они вызывают сжатие. Отметим также, что величины внутренних усилий не изменяются по длине стержня и, таким образом, распределение нормальных напряжений в сечениях, достаточно удаленных от места приложения нагрузки, будет одинаковым.
Подставив (11.11) в (11.1), получим формулу для определения нормальных напряжений при внецентренном сжатии:

Эту формулу можно преобразовать к виду

где iy, iz — главные радиусы инерции сечения, определяемые по формулам:

Приравняв выражение (11.12) к нулю, получим уравнение нулевой линии

Полагая в этом уравнении последовательно у = 0 и z — 0, получим формулы для определения отрезков, отсекаемых нулевой линией на осях координат:

Отложив эти отрезки на осях, проведем нулевую линию (рис. 11.13), в каждой точке которой о = 0. Отметим, что при внецентренном сжатии (растяжении) нулевая линия не проходит через центр тяжести сечения, а ее положение не зависит от величины силы Р.
Поскольку знаки величин ^и^ противоположны знакам соответственно zp и у , нулевая линия проходит через те четверти системы координат, которые не содержат точки приложения силы (рис. 11.13).

Рис. 11.13
Рис. 11.14
Положение нулевой линии зависит от геометрических характеристик сечения и от координат точки приложения силы. При этом величины Zq, zp и у0, ^являются обратно пропорциональными по отношению друг к другу.
Исследуем изменение положения нулевой линии при перемещении точки приложения силы вдоль прямой, проходящей через центр тяжести сечения. Из формул (11.14) следует, что все нулевые линии будут при этом параллельными, причем при приближении точки приложения силы к центру тяжести сечения величины zp и у уменьшаются и нулевая линия удаляется от него, и наоборот (рис. 11.14).
Нетрудно доказать также следующее положение. Если точка приложения силы перемещается вдоль прямой, не проходящей через центр тяжести сечения, то нулевая линия поворачивается относительно некоторой точки (рис. 11.15). Справедливо и обратное утверждение. Это свойство используется при построении особой фигуры — ядра сечения.

Рис. 11.16
Рис. 11.15
Нормальные напряжения в сечении изменяются по линейному закону, увеличиваясь по абсолютной величине по мере удаления от нулевой линии. Эпюра о строится на прямой, перпендикулярной к нулевой линии. При этом она может быть разнозначной или однозначной (см. рис. 11.14). Последнее имеет место в случае, если точка приложения силы Р расположена вблизи центра тяжести сечения. Напомним, что при центральном сжатии или растяжении нормальные напряжения являются одинаковыми по величине, а эпюра с представляет собой прямоугольник.
В точках прямой, проходящей через центр тяжести сечения и параллельной нулевой линии, нормальные напряжения равны °о =—P/F.
Рассмотрим случай разнозначной эпюры с (рис. 11.14, а). Так же как и при косом изгибе, наибольшие растягивающие и сжимающие напряжения действуют в точках сечения, наиболее удаленных от нулевой линии (угловые точки А и В на рис. 11.14). Для произвольного сечения эти точки и их координаты устанавливаются с помощью касательных к сечению, параллельных нулевой линии (например, точка А на рис. 11.16). В общем случае онбф |онм|.
Если материал стержня неодинаково сопротивляется растяжению и сжатию, то необходимо обеспечить выполнение двух условий прочности по наибольшим растягивающим и наибольшим сжимающим напряжениям в точках А и В:

где Rp и Rc — расчетные сопротивления материала при растяжении и сжатии; zA, УА и zB, У в ~ координаты наиболее напряженных точек сечения.
Из условий прочности (11.15) можно определить величину предельной расчетной силы.
Для стержней из материала, одинаково сопротивляющегося растяжению и сжатию (R^ = Rc = R), а также в случае однозначной эпюры о (рис. 11.14, б) достаточно обеспечить выполнение одного условия прочности по точке с наибольшими по абсолютной величине напряжениями.
В инженерной практике чаще имеет место случай внецент- ренного сжатия (или растяжения), когда точка приложения силы Р расположена на одной из главных осей (рис. 11.17, а). При этом согласно формулам (11.14) нулевая линия параллельна другой главной оси (рис. 11.17, б). Нормальные напряжения определяются по двухчленной формуле. Например, для случая, показанного на рис. 11.17, имеем


Рис. 11.17
Многие строительные материалы (бетон, кирпичная кладка, чугун и др.) плохо сопротивляются растяжению. Поэтому в элементах конструкций из таких материалов, работающих на вне- центренное сжатие, нежелательно появление растягивающих нормальных напряжений. Это условие будет выполнено, если точка приложения силы расположена внутри или на границе некоторой области вокруг центра тяжести, которая называется ядром сечения.
Граница или контур ядра строится с помощью нулевых линий, которые являются касательными к сечению. При этом координаты точек контура ядра определяются с помощью формул
(11.14):

Здесь у0, Zq — координаты точек пересечения нулевых линий, касательных к контуру сечения, с осями координат; ур, zp — координаты точек контура ядра, соответствующие положению данной касательной.
Таким образом, если точка приложения силы расположена на контуре ядра, то нулевые линии являются касательными к сечению, а эпюра с представляет собой треугольник. При приложении силы внутри ядра нулевая линия проходит вне сечения (условная нулевая линия) и эпюра о является трапецией.
Ядро сечения содержит центр тяжести и является выпуклой фигурой, поскольку соответствующие границе ядра нулевые линии должны касаться огибающей контура сечения и не пересекать его.
При построении контура ядра его точки надо соединить соответствующими линиями. Если нулевые линии, касательные к сечению, перемещаются при переходе от одного положения к другому путем поворота вокруг угловых точек, то на основании изложенного выше положения линии контура ядра являются прямыми.

Рис. 11.18

Рис. 11.19

Рис. 11.20
Построим ядро сечения для некоторых фигур. Для прямоугольника достаточно провести две нулевые линии, являющиеся касательными к сечению (рис. 11.18). Для касательной 1 — 1 имеем у() = И/2 и Zq= °°. Учитывая, что

определяем координаты точки 1 контура ядра сечения:

Аналогично для касательной 2—2 находим координаты точки 2: zp = — b/6, ур = 0. Точки 3 и 4 расположены симметрично по отношению к точкам 1 и 2. Ядро сечения представляет собой ромб с длинами диагоналей h/З и Ь/3 (рис. 11.18).
Ядро сечения для двутавра также представляет собой ромб, значительно вытянутый вдоль оси Оу (рис. 11.19), поскольку J. » Jy. Ядро сечения для швеллера является четырехугольником, симметричным относительно оси Oz (рис. 11.20).
При построении ядра сечения для круга достаточно провести одну касательную 1—1 (рис. 11.21), для которой у0 = R, Zq = °°.

Рис. 11.21

Рис. 11.22
Учитывая, что для круга

находим координаты точки 1:

Очевидно, что ядро сечения для круга представляет собой также круг с радиусом г = R/4. Такой же вид имеет ядро для кольцевого сечения (рис. 11.22), однако радиус ядра значительно больше, чем для сплошного круга. Нетрудно показать, что при 5 « R2 радиус ядра сечения приближенно равен Rq/2, где Rq — средний радиус кольца.

Рис. 11.23
При построения ядра сечения, показанного на рис. 11.23, достаточно провести четыре касательные к сечению и определить координаты четырех точек контура ядра. Точки 1, 2 и 3 надо соединить прямыми линиями. Контур ядра между точками 3, 4 является криволинейным. Точки 5 и 6 симметричны по отношению к точкам 3 и 2.
Пример 11.5. Для короткого чугунного стержня коробчатого сечения, испытывающего внецентренное сжатие (рис. 11.24, а), определим расчетную величину силы Р из условий прочности. Построим эпюру о и ядро сечения. В расчетах примем Rp = = 50 МПа = 5 кН/см2, Rc = 150 МПа = 15 кН/см2 и ус = 1,0.

Рис. 11.24
Определяем необходимые геометрические характеристики сечения (рис. 11.24, б):

Координаты точки приложения силы Р равны: ур = 6 см, zp — = —4,5 см. Определяем по формулам (11.14) величины отрезков, отсекаемых нулевой линией на осях координат:

Отложив эти отрезки на осях, проводим нулевую линию, которая пересекает сечение и делит его на зоны растяжения и сжатия. Эпюра с является разнозначной (рис. 11.24, б). Наибольшие растягивающие и сжимающие напряжения действуют в угловых точках Ли В, наиболее удаленных от нулевой линии. Координаты этих точек равны: уА = —6 см, zA = 4,5 см, ув= 6 см, zB = —4,5 см.
Из условий прочности при растяжении и сжатии находим два значения расчетной силы Р:

Для обеспечения прочности стержня в зонах растяжения и сжатия принимаем с округлением меньшую силу Р = 100 кН. При этом напряжения в точках Ли В равны:

Прочность стержня обеспечена. Эпюра о приведена на рис. 11.24, б.
Для построения ядра сечения достаточно провести две нулевые линии, касательные к контуру сечения, и определить координаты двух точек контура ядра.
Касательная 1—1:

Касательная 2—2:

Проведенные касательные соответствуют точкам 1 и 2 контура ядра сечения. Симметрично расположены точки 3 и 4. Поскольку касательные переходят из одного положения в другое путем поворота вокруг угловых точек сечения, все линии контура ядра являются прямыми. Ядро сечения представляет собой ромб (рис. 11.24, б). Так как точка приложения силы принадлежит одновременно касательным 1—1 и 2—2 , нулевая линия проходит по линии контура ядра 1—2.
Пример 11.6. Для короткого стального стержня составного сечения, находящегося в условиях внецентренного сжатия (рис. 11.25, а), определим величину расчетной силы Риз условия прочности. В расчетах примем Р = 210МПа = 21 кН/см2 и ус = 0,9. Построим эпюру о и ядро сечения.
Поскольку zp = 0, данная задача относится к частному случаю внецентренного сжатия. Определяем необходимые геометрические характеристики сечения:

Определяем положение нулевой линии:


Рис. 11.25
Нулевая линия параллельна оси Oz и не пересекает сечение. Эпюра а является однозначной (рис. 11.25, б). Наибольшие сжимающие напряжения действуют в крайних верхних точках сечения (у = ув = —11 см). Из условия прочности определяем расчетное значение силы Р:

При действии силы Р = 744 кН наибольшие сжимающие напряжения в крайних верхних точках сечения по абсолютной величине равны уCR = 189 МПа. Определяем напряжения в крайних нижних точках сечения (у = уА= 11 см):

Напряжения в поперечных сечениях стержня являются сжимающими. Эпюра а приведена на рис. 11.25, б.
Ядро сечения представляет собой ромб, координаты вершин которого определяем с помощью двух касательных к сечению. Касательная 1—1:

Касательная 2—2:

Точка приложения силы расположена внутри ядра сечения (рис. 11.25, б).
Источник
Основные
определения
Внецентренное
растяжение-сжатие
– такой вид деформации, при котором
стержень загружен растягивающими и
(или) сжимающими силами, приложенными
вне центра тяжести поперечного сечения.
При внецентренном растяжении-сжатии
стержней (рис. 5.9) в стержне возникают
три внутренних усилия: продольная сила
![]() и два изгибающих момента
и два изгибающих момента![]() и
и![]() .
.
Предполагается, что стержень имеет
большую жесткость, т. е. его длина не
слишком велика по сравнению с размерами
поперечного сечения. В этом случае
определение усилий производим по
недеформированному состоянию, т. е. при
определении усилий не учитываем
искривление оси стержня в результате
изгиба. Используя правило знаков для
изгибающих моментов, описанное во
вступительной части разд. 5 «Сложное
сопротивление», найдем внутренние
усилия, как сумму усилий от каждой силы.
Тогда для стержня, показанного на
рис. 5.9, согласно методу сечений
получим
![]() ;
;
![]() ;
;
![]() .
.
Здесь
![]() – эксцентриситеты точек приложения
– эксцентриситеты точек приложения
сил, т. е. расстояния от сил до осей![]() и
и![]() (всегда положительны),
(всегда положительны),![]() и
и![]() –
–
величины сил тоже считаются положительными.
Знаки в формулах для![]() и
и![]() соответствуют правилу знаков для
соответствуют правилу знаков для
изгибающих моментов. Поясним их.
Относительно оси![]() сила
сила![]() вызывает изгиб стержня выпуклостью
вызывает изгиб стержня выпуклостью
справа. Вся область сечения, расположенная
справа от оси![]() ,
,
в том числе и первый (положительный)
квадрант, окажется растянутой, поэтому
эта сила создает положительный изгибающий
момент. Сила![]() вызывает изгиб стержня относительно
вызывает изгиб стержня относительно
оси![]() тоже выпуклостью справа, поэтому знак
тоже выпуклостью справа, поэтому знак
изгибающего момента![]() от силы
от силы![]() опять положительный. При изгибе
опять положительный. При изгибе
относительно оси![]() передняя и задняя части сечения имеют
передняя и задняя части сечения имеют
напряжения разного знака. Сила![]() вызывает изгиб стержня выпуклостью за
вызывает изгиб стержня выпуклостью за
осью![]() ,
,
т. е. задняя часть сечения (а значит и
первый квадрант) окажется растянутой,
поэтому![]() от силы
от силы![]() имеет знак плюс. Сила
имеет знак плюс. Сила![]() вызывает сжатие задней части сечения
вызывает сжатие задней части сечения
стержня, первый квадрант окажется
сжатым, и знак изгибающего момента![]() от
от![]() отрицательный7.
отрицательный7.
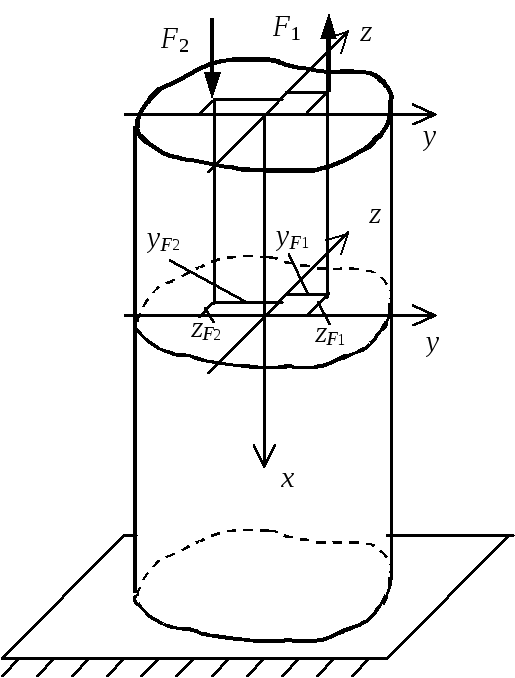
Рис. 5.9. Внецентренное растяжение-
сжатие жесткого стержня
От найденных усилий в
стержне возникают только нормальные
напряжения, которые определяются по
формуле (5.1). Для проверки прочности
стержня необходимо найти максимальные
напряжения. Определение этих напряжений
производится по схеме, описанной ранее,
т. е.
строим нейтральную
линию по уравнению (5.2);находим положение
опасных точек;подставляя в (5.1)
координаты опасных точек, вычисляем
напряжения в этих точках;для проверки
прочности сравниваем максимальные
напряжения с допускаемыми.
Если в сечении
действует только одна сила, растягивающая
или сжимающая , то формулу (5.1) можно
преобразовать к такому виду:
![]() ,
,
(5.9)
где
![]() ,
,
![]() (5.10)
(5.10)
– радиусы инерции
сечения относительно главных центральных
осей,
![]() ,
,![]() – координаты точки приложения силы,
– координаты точки приложения силы,![]() ,
,![]() – координаты точки, в которой определяются
– координаты точки, в которой определяются
напряжения. Все координаты вычисляются
вглавной
центральной
системе осей инерции сечения. Уравнение
нейтральной линии в этом случае будет
иметь вид
![]() .
.
(5.11)
Используя уравнение
нейтральной линии (5.11), найдем отрезки
![]() ,
,![]() ,
,
отсекаемые нейтральной линией на осях
координат (рис. 5.10),
![]() ;
; ![]() .
.
(5.12)
Откладываем эти
отрезки с учетом знаков вдоль главных
центральных осей и строим нейтральную
линию (см. рис. 5.10).

Рис. 5.10. Положение нейтральной линии
при внецентренном растяжении (сжатии)
одной силой
Из формул (5.12) следуют
некоторые закономерности, связывающие
положения полюса (т. е. точки приложения
силы) и нейтральной линии, которые удобно
использовать для анализа решения задачи.
Перечислим самые важные из этих
закономерностей:
нейтральная линия
всегда расположена в квадранте,
противоположном тому, в котором находится
полюс (см. рис. 5.10);если полюс
находится на одной из главных осей, то
нейтральная линия перпендикулярна
этой оси;если полюс
приближается к центру тяжести сечения,
то нейтральная линия удаляется от него.если полюс движется
по прямой линии, то нейтральная линия
поворачивается вокруг неподвижной
точки.

Рис. 5.11. К определению ядра сечения
Из предпоследней закономерности
следует, что если сила приложена
достаточно близко к центру тяжести, то
нейтральная линия удаляется так далеко,
что нигде не пересекает сечение. Это
означает, что напряжения во всем сечении
будут иметь один знак. Следовательно,
существует такая область вокруг центра
тяжести, которая обладает следующим
свойством: если внутри этой области или
на ее контуре приложить силу (растягивающую
или сжимающую), то во всем
сечении будут возникать напряжения
одного знака. Такая область называется
ядром сечения.
Рис. 5.11 поясняет данное определение
ядра сечения.
Из приведенного
определения ядра сечения следует первый
способ
построения ядра сечения. Согласно этому
способу надо обвести контур сечения
нейтральными линиями, касающимися
контура и нигде не пересекающими сечение.
Полюсы, соответствующие этим нейтральным
линиям, будут находиться на контуре
ядра сечения. На практике обычно более
удобным является второй способ построения
ядра сечения, который основан на свойстве
взаимности нейтральной линии и полюса
[2,
гл. 7,
§
36].
Для построения ядра сечения по второму
способу надо
поместить полюсы во внешних всех угловых
точках сечения, имеющего форму
многоугольника, и построить соответствующие
им нейтральные линии. Эти нейтральные
линии очертят контур ядра сечения.
Отметим, что при построении ядра сечения
нельзя располагать полюсы во внутренних
угловых точках, так как через них нельзя
провести касательные, нигде не пересекающие
сечение. Рис. 5.12 поясняет разницу
между внешними и внутренними угловыми
точками многоугольника.
Для определения
напряжений и проверки прочности стержня
произвольного сечения, а также для
построения ядра сечения необходимо
научиться находить геометрические
характеристики сечений, важнейшими из
которых являются моменты инерции. Этому
посвящен раздел 5.2.1.
Соседние файлы в папке сопр задания
- #
- #
- #
- #
Источник
Исходные данные
Материал – кирпич керамический на ц.п. растворе. Марка кирпича М250, марка раствора М200. Расчётное сопротивление кладки сжатию R=36.7098 кгс/см2, Rt=0.815773 кгс/см2, Ru=2*R=2*36.7098=73.4196 кгс/см2, Rtu=2*Rt=2*0.815773=1.631546 кгс/см2. Размеры простенка b=38 см, h=100 см. Высота простенка l0=450 см. По результатам определения внутренних усилий в сечении простенка возникают следующие усилия: N=100 т, изгибающие моменты Мх=0 т*м, Му=1.075 т*м, поперечные силы, Qx=-0.378 т, Qy=0 т. Изгибающий момент действует в направлении стороны b
Расчёт на внецентренное сжатие в плоскости изгиба
По п.7.7 Расчет внецентренно сжатых неармированных элементов каменных конструкций следует производить по формуле
N<=φ1*mg*R*Ac*ω
mg=1 — коэффициент, учитывающий влияние длительной нагрузки и определяемый по формуле (16). При толщине стены более 30 см, принимается равным 1.
φ1x=(φx+φcx)/2
Для l0=450 см, ix=0.289*100=28.9 см, α=1000, по таблице 19, при λ=l0/ix=450/28.9=15.57, φ=0.99103
| αn | ||
| 1000 | ||
| λn | 14 | 1 |
| λi | 15.57 | 0.99103 |
| λn+1 | 21 | 0.96 |
φс — коэффициент продольного изгиба для сжатой части сечения, определяемый по фактической высоте элемента Н по таблице 18 в плоскости действия изгибающего момента при гибкости:
λiс=H/iс
где hс и iс — высота и радиус инерции сжатой части поперечного сечения Ас в плоскости действия изгибающего момента.
Площадь сжатой части сечения принимается равной площади сечения:
Ac=A=3800
A=b*h=3800 см2 — площадь поперечного сечения простенка;
e0y=Mx/N=0.919 см — эксцентриситет расчётной силы N относительно центра тяжести сечения;
ev=0 см — случайный эксцентриситет продольной силы, принимаемый равным 0, для стен толщиной более 25 см.
Высота сжатой части сечения hсx=b=100 см;
Радиус инерции сжатой части сечения icx=0.289*hcx=0.289*100=28.9 см, λcx=l0/icb=450/28.9=15.57, φcx=0.99103
| αn | ||
| 1000 | ||
| λn | 14 | 1 |
| λi | 15.57 | 0.99103 |
| λn+1 | 21 | 0.96 |
Коэффициент продольного изгиба: φ1x=(φx+φcx)/2=(0.99103+0.99103)/2=0.99103
Коэффициент ω=1+ex/h=1+1.075/100=1.011 — для кладки из керамического кирпича
Подставляя данные в формулу прочности простенка, получаем:
N=100 т<=φ1x*mg*R*Ac*φx=0.99103*36.7098*1*3800*1.011=139.76666 т
Коэффициент запаса 139.76666/100=1.39767
Расчёт на центральное сжатие из плоскости изгиба
По п.7.1 Расчет внецентренно сжатых неармированных элементов каменных конструкций следует производить по формуле (10):
N<=φy*mg*R*A
Определение коэффициента продольного изгиба
Для l0=450 см, iy=0.289*38=10.982 см, α=1000, по таблице 19, при λ= l0/iy=450/10.982=40.976, φ=0.84585
| αn | ||
| 1000 | ||
| λn | 35 | 0.88 |
| λi | 40.976 | 0.84585 |
| λn+1 | 42 | 0.84 |
Подставляя значения в формулу (10), получаем:
N=100 т<=φy*mg*R*A=0.84585*1*36.7098*3800=117.99374 т
Характеристики материалов каменных конструкций, заданных для расчёта в программе
Расчёт в ПК ЛИРА САПР, выполняется по СП 15.13330.2012 по нелинейной деформационной модели кладки.
Характеристики материалов:

Характеристики материалов
Сравнение результатов ручного расчёта с программным счётом
Сравнение выполним в табличной форме
| Параметр для сравнения | Результат расчёта | Погрешность | |
| Ручной расчёт | ЛИРА-САПР | ||
| Коэффициент запаса прочности кладки при сжатии | 1.17994 | 1.18 | 0.01% |
Коэффициент запаса прочности кладки в ПК ЛИРА САПР
Подбор армирования кирпичной кладки
Исходные данные
Выполним расчёт конструкции из предыдущего примера с уменьшенными марками кирпича и раствора. Марка кирпича М150, марка раствора М100. Расчётное сопротивление кладки сжатию R=22.432828 кгс/см2.
Несущая способность простенка при центральном сжатии:
Высота простенка и размеры поперечного сечения такие же, как при проверке неармированной кладки.
N=100 т>φy*mg*R*A=0.84585*1*22.432828*3800=72.104269 т — условие не выполняется, требуется сетчатое армирование.
Принимаем армирование сетками из арматуры В500, Rs=4435.77 кгс/см2, диаметр стержней 4 мм, шаг стержней 50×50 мм. Сетки устанавливаются через три ряда, при высоте ряда кладки 100 мм, шаг сеток будет равен 30 см. Определим расчётное сопротивление армированной кладки:
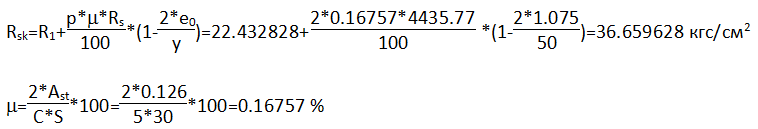
Ввиду того, что простенок является внецентренно нагруженным, расчёт прочности кладки с сетчатым армированием, выполняется по формуле (31) СП 15.13330.2012
Проверка условия Rsk≤2*R
36.659628<2*22.432828 – условие выполняется, принимаем Rsk=36.659628 кгс/см2.
Определим упругую характеристику кладки с сетчатым армированием:
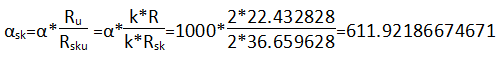
Расчёт несущей способности армированной кладки. Для l0=450 см, iy=0.289*38=10.982 см, по таблице 19, при λ=l0/iy=450/10.982=40.976, 0.75999506029.
| αn | αi | αi+1 | ||
| 750 | 611.92186674671 | 500 | ||
| λn | 35 | 0.84 | 0.81238437335 | 0.79 |
| λi | 40.976 | 0.797 | 0.75999506029 | 0.73 |
| λn+1 | 42 | 0.79 | 0.72 | |
Подставляя данные в формулу прочности простенка, получаем:
N=100 т>φy*mg*Rsk*A=0.75999506029*1*36.659628*3800=105.87231752986 т
Условие прочности выполняется. Коэффициент запаса 105.87231752986/100=1.0587231753
Характеристики материалов каменных конструкций, заданных для расчёта в программе
Расчёт в ПК ЛИРА САПР, выполняется по СП 15.13330.2012 по нелинейной деформационной модели кладки.
Характеристики материалов:

Характеристики материалов
Сравнение выполним в табличной форме
| Параметр для сравнения | Результат расчёта | Погрешность | |
| Ручной расчёт | ЛИРА-САПР | ||
| Коэффициент запаса прочности кладки при сжатии | 1.0587231753 | 1.07 | 1.07% |
Коэффициент запаса прочности кладки в ПК ЛИРА САПР
Источник
