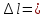Расчет на прочность при растяжении и сжатии практическая работа

государственное автономное учреждение
Калининградской области
профессиональная образовательная организация
Колледж сервиса и туризма
Методические рекомендации
по выполнению практических работ
«Сопротивление материалов»
по дисциплине Техническая механика
для студентов 3 курса
специальности 20.02.04 Пожарная безопасность
Калининград
УТВЕРЖДАЮ
Заместитель директора по УР ГАУ КО ПОО КСТ Н.Н. Мясникова
ОДОБРЕНО
Методическим советом ГАУ КО ПОО КСТ
РАССМОТРЕНО
На заседании ПЦК технологических дисциплин
Редакционная коллегия:
Колганова А.А., методист
Фалалеева А.Б., преподаватель русского языка и литературы
Цветаева Л.В.., председатель ПЦК общематематических и естественнонаучных дисциплин
Составитель:
Незванова И.В. преподаватель ГАУ КО ПОО КСТ
Содержание
Практическое занятие 6: Расчёты на прочность и жёсткость при растяжении и сжатии
4
Практическая работа 7: Геометрические характеристики плоских сечений
9
Практическая работа 8: Кручение. Расчёты на прочность и жесткость при кручении
11
Практическая работа 9: Расчёты на прочность при изгибе
14
Практическая работа 10: Расчёты бруса круглого поперечного сечения при сочетании основных деформаций.
17
Приложение
19
Список литературы
23
Практическое занятие 6
Расчёты на прочность и жёсткость при растяжении и сжатии
Необходимые формулы
Нормально напряжение
где N- продольная сила; А- площадь поперечного сечения.
Удлинение (укорочение) бруса
Е-модуль упругости; l- начальная длина стержня.
Допускаемое напряжение
[s]-допускаемые запасы прочности.
Условие прочности при растяжении и сжатии:
Примеры расчётов на прочность и сжатие
Пример 1: Груз закреплён на стержнях и находится в равновесии (рисунок 6.1). Материал стержней – сталь, допускаемое напряжение 160 МПа. Вес груза 100кН. Длина стержней: первого – 2м, второго – 1м. Определить размеры поперечного сечения и удлинение стержней. Форма поперечного сечения – круг.
Рисунок 6.1
Решение:
1. Определить нагрузку на стержни. Рассмотрим равновесие точки В, определим реакции стержней. По пятой аксиоме статики (закон действия и противодействия) реакция стержня численно равна нагрузке на стержень.
Наносим реакции связей, действующих в точке В. Освобождаем точку В от связей. (рисунок 6.1)
Выбираем систему координат так, чтобы одна из осей координат совпадала с неизвестной силой. (рисунок 6.1. б)
Составим систему уравнений равновесия для точки В:
Решим систему уравнений и определяем реакции стержней.
Направление реакций выбрано верно. Оба стержня сжаты. Нагрузки на стержни: F1=57,4kH; F2=115,5kH.
2. Определяем потребную площадь поперечного сечения стержней из условий прочности.
Условие прочности на сжатие:
откуда
Стержень 1 (N1=F1)
Для круга
Стержень 2 (N2=F2)
Полученные диаметры округляем: d1=25мм, d2=32мм.
3. Определяем удлинение стержней
Укорочение стержня 1:
Укорочение стержня 2:
Пример 2: Однородная жесткая плита с силой тяжести 10кН, нагруженная силой F=4,5кН и моментом m=3 кН*м, оперта в точке А и подвешена на стержень ВС (рисунок 6.2). Подобрать сечение стержня в виде швеллера и определить его удлинение, если длина стержня 1м, материал – сталь, предел текучести 570 МПа, запас прочности для материала 1,5.
Решение:
1. Определить усилие в стержне под действием внешних сил.
Система находится в равновессии, можно использовать уравнение равновессия для плиты:
RB – реакция стержня, реакции шарнира А не рассматриваем.

Откуда
По третьему закону динамики реакция в стержне равна силе, действующей от стержня на плиту. Усилие в стержне равно 14 кН.
Рисунок 6.2
2. По условию прочности определяем потребную величину площади поперечного сечения:
, откуда
Допускаемое напряжение для материала стержня:
Следовательно
3. Подберём сечение стержня по ГОСТ (Приложение 1)
Минимальная площадь швелера 6,16см2
Целесообразнее оспользовать равнополочный уголок №2 (d=3мм), площадь поперечного сечения которого 1,13 см2.
4. Определить удлинение стержня
Расчётно-графическая работа
Задание 1: Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса. Двухступенчатый стальной брос нагружен силами F1, F2,F3.Площадь поперечного сечения А1 и А2.
Принять
Рисунок 6.3
Задание 2: Балка АВ, на которую действуют указанные нагрузки, удерживается в равновесии тягой ВС. Определить размеры поперечного сечения тяги для двух случаев: 1) сечение – круг; 2)сечение – уголок равнополочный. Принять . Собственный вес конструкции не учитывать.

Рисунок 6.4
Практическая работа 7
Геометрические характеристики плоских сечений
Моменты инерции простейших сечений
Прямоугольник и квадрат (Рисунок 7.1)
Осевые:
Jx-относительно оси хх
Jy-относительно оси yy
Полярный: Jp=Jx+Jy
Рисунок 7.1
Круг и кольцо (рисунок 7.2)
Осевые: — круг;
—кольцо
Полярные — круг;
— кольцо.
Рисунок 7.2
Моменты инерции относительно параллельных прямых (рисунок 7.3)
,
гдеJx— момент инерции относительно оси хх;
Jx0 — момент инерции относительно оси х0х0;
Рисунок 7.3
А-площадь сечения; а- расстояние между осями.
Рекомендации для решения задач расчетно–графической работы.
1. Момент инерции сложной фигуры является суммой моментов инерции частей, на которые ее разбивают. Разбить заданную фигуру на простейшие части, для каждой определить главные центральные моменты инерции по известным формулам.
2. Моменты инерции вырезов и отверстий можно представить отрицательными величинами.
3. Заданные сечения симметричны, главные центральные оси совпадают с осями симметрии составного сечения.
4. Моменты инерции частей, чьи главные центральные оси не совпадают с главными центральными осями сечения в целом, пересчитывают с помощью формулы для моментов инерции относительно параллельных осей. Расстояние между параллельными осями определить по чертежу.
5. При выполнении задания 2 главные центральные моменты инерции отдельных стандартных профилей определить по таблицам ГОСТ (Приложение 1).
Для использованных в составных сечениях полос моменты инерции определить по известной формуле для прямоугольника.
Расчетно-графическая работа
Геометрические характеристики плоских сечений
Задание 1: Вычислить главные центральные моменты инерции сечений, представленных на схемах (рисунок 7.4). При расчётах воспользоваться данными таблицы, выбрав необходимые значения.

Рисунок 7.4

Практическая работа 8
Кручение. Расчёты на прочность и жёсткость при кручении.
Основные положения расчётов при кручении
Распределение касательных напряжений по сечению при кручении (рисунок 8.1).
Касательное напряжение в точке А: 
, где ρА—расстояние от точки А до центра сечения.
Условие прочности при кручении
Рисунок 8.1
Мк — крутящий момент в сечении, Н*м
Wp – момент сопротивления при кручении, м3
— допускаемое напряжение при кручении, Н/м2
Проектировочный расчёт, определение размеров поперечного сечения
Сечение-круг:
Сечение – кольцо:
где d – наружный диаметр круглого сечения;
dвн- внутренний диаметр кольцевого сечения; с= dвн/ d
Определение рационального расположения колёс на валу
Рациональное расположение колес – расположение, при котором максимальное значение крутящего момента на валу – наименьшее из возможных.
Для экономии металла сечение бруса рекомендуется выполнять кольцевым.
Условие жесткости при кручении
G – модуль упругости при сдвиге, Н/м2
E – модуль упругости при растяжении, Н/м2
– допускаемый угол закручивания,
— полярный момент инерции в сечении, м4
Проектировочный расчёт, определение наружного диаметра сечения
Рекомендации по выполнению расчетно-графической работы
1. Построить эпюру крутящих моментов по длине вала для предложенной в задании схемы.
2. Выбрать рациональное расположение колес на валу и дальнейшие расчеты проводить для вала с рационально расположенными шкивами.
3. Определить потребные диаметры вала круглого сечения из расчета на прочность и жесткость и выбрать наибольшее из полученных значений, округлив величину диаметра. 4. Сравнить затраты металла для случая круглого и кольцевого сечений. Сравнение провести по площадям поперечных сечений валов.
Площади валов рассчитать в наиболее нагруженном сечении (по максимальному крутящему моменту на эпюре моментов).
Расчетно-графическая работа
Для стального вала круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям, и уравновешенный момент.
Построить эпюру крутящих моментов по длине вала.
Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
Построить эпюру крутящих моментов для этого случая.
Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного или оканчивающегося на 5 числа.
При расчете использовать следующие данные: вал вращается с угловой скоростью 25 рад/ с; материал вала — сталь, допускаемое напряжение кручения 30 МПа, модуль упругости при сдвиге 8-104 МПа; допускаемый угол закручивания = 0, 02 рад/ м.
Провести расчет для вала кольцевого сечения, приняв с = 0,9.
Сделать выводы о целесообразности выполнения вала круглого или кольцевого сечения, сравнив площади поперечных сечений.


Рисунок 8.2
Практическая работа 9
Расчёты на прочность при изгибе
Основные положения и расчётные формулы при изгибе
Распределение нормальных и касательных напряжений при изгибе
где Ми – изгибающий момент в сечении;
Q-поперечная сила в сечении;
Рисунок 9.1
у – расстояние до нейтрального слоя;
Jx- осевой момент инерции сечения (рисунок 9.1)
Wx – осевой момент сопротивления сечения; А-площадь сечения
Условие прочности при изгибе
где – допускаемое напряжение
Знаки изгибающих моментов и поперечных сил (рисунок 9.2)
Рисунок 9.2
Расчётно-графическая работа
Задание 1: Для одноопорной балки, нагруженной сосредоточенными силами и парой сил с моментом m, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный изгибающий момент и из условия прочности подобрать поперечное сечение для балки в виде двутавра и прямоугольника с отношением сторон h=2b. Материал – сталь, допускаемое напряжение 160 МПа. Рассчитать площади поперечных сечений и сделать вывод о целесообразности применения сечения. Для выбора профелей балок использовать приложение 1.
Рисунок 9.3
Задание 2: Для двухопорной балки, нагруженной сосредоточенными силами и парой сил с моментом, определить реакции в опорах. Найти максимальный изгибающий момент и используя условие прочности, подобрать необходимые размеры поперечных сечений. Материал – сталь, допускаемое напряжение изгиба 160 Мпа. Сечение – швелер.
Рисунок 9.4
Практическая работа 10
Расчёты бруса круглого поперечного сечения при сочетании основных деформаций.
Основные положения и расчётные формулы
Геометрические характеристики круга и кольца
Круг (рисунок 10.1)
— круг;
Рисунок 10.1
Кольцо (рисунок 10.2)
Рисунок 10.2
Моменты сопротивления:
Площади сечения
Условие прочности при совместном действии изгиба и кручения.
Эквивалентные моменты
Расчетно-графическая работа
Для промежуточного вала редуктора, передающего мощность Р при угловой скорости ω, определить вертикальную и горизонтальную составляющие реакции подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметры вала по сечениям, приняв [σ] – 60 МПа и полагая FT- 0,364 Ft. Расчёт произвести по гипотезе максимальных касательных напряжений.
Рисунок 10.3
Указание: Окружную силу определить по формуле
Приложение № 1
Сталь горячекатная. Швеллеры.
Обозначение:
h- высота швеллера; b- ширина швеллера
d- толщина стенки; t-средняя толщина полки
А- площадь швеллера
J- момент инерции
W- момент сопротивления
i – радиус инерции
S – статический момент полусечения
Z0- расстояние от оси у до наружной грани стенки
Таблица 1
Сталь горячекатная. Балки двутавровые.
Обозначение:
h- высота балки ;b- ширина балки
d- толщина стенки; t-средняя толщина полки
А- площадь сечения; J- момент инерции
W- момент сопротивления
i – радиус инерции
S – статический момент полусечения
Таблица 2
Сталь прокатная угловая равнополочная.
Обозначение:
b- ширина полки;
d- толщина полки;
А- площадь уголка;
W- момент сопротивления
i – радиус инерции
Z0- расстояние от оси у до наружной грани полки
J- момент инерции
Таблица 3
Продолжение таблицы 3
Список литературы
Олофинская В.П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий: учебное пособие / В.П.Олофинская – 3-е издание – М.: ФОРУМ, 2012 – 352 стр.
Источник
Если внешняя сила направлена от сечения, то продольная сила положительна, брус растянут; если внешняя сила направлена к сечению, то продольная сила отрицательна, брус сжат.
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси бруса.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
На эпюре проставляются значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе.
Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.
При растяжении и сжатии в сечении действует только нормальное напряжение, которое определяется по формуле:
,
где N – продольная сила в сечении,
А — площадь поперечного сечения.
При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений. Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.
Строится и оформляется такая эпюра так же, как и эпюра продольных сил.
Расчеты на прочность ведутся по условиям прочности — неравенствам, выполнение которых гарантирует прочность детали при данных условиях.
Для обеспечения прочности расчетное напряжение не должно превышать допускаемого напряжения:
σ ≤ [σ], где σ =
Расчетное напряжение σ зависит от нагрузки и размеров поперечного сечения, допускаемое только от материала детали и условий работы.
Существуют три вида расчета на прочность.
1. Проектировочный расчет — задана расчетная схема и нагрузки. Необходимо подобрать размеры детали:
А=
2. Проверочный расчет — известны нагрузки, материал, размеры детали; необходимо проверить, обеспечена ли прочность.
Проверяется неравенство σ ≤ [σ]
3. Определение нагрузочной способности (максимальной нагрузки): [N] = [σ]А.
Литература: Олофинская механика. Курс лекций с вариантами практических и тестовых заданий: учебное пособие. — 2-е изд. — М.: ФОРУМ: ИНФРА-М, 2012.
Проверка знаний и умений (необходимых для выполнения практической работы)
№ п/п | Задание | Вариант ответа |
1. | Какая из эпюр, приведенных на рисунке, соответствует эпюре продольных сил стержня?
| A. Б. B. |
2. | Укажите эпюру, соответствующую эпюре нормальных напряжений для данного бруса
| A. Б. B. |
3. | Обеспечена ли прочность бруса в сечении С-С, если допустимое напряжение [σ] = 260 МПа?
| A. σ < [σ] . B. σ = [σ]; С. σ > [σ]; |
Задание.
Для стального бруса круглого поперечного сечения диаметром D требуется:
1) построить эпюры продольных сил и нормальных напряжений;
2) проверить прочность стержня, если [σ] = 160МПа. Данные своего варианта взять из таблицы.
Порядок выполнения работы:
1. Изобразить расчётную схему.
2. Разделить брус на участки нагружения, границы которых находятся в точках приложения сил.
3. Определить продольные силы на участках бруса, используя метод сечений.
4. Провести нулевую линию параллельно оси бруса.
5. Найденные величины продольных сил отложить в масштабе в виде ординат, перпендикулярных оси бруса (положительные значения вверх от нулевой линии, отрицательные вниз). Через концы ординат провести линии параллельно оси бруса; поставить знаки и заштриховать эпюру параллельно ординатам.
6. Разделить брус на участки нагружения для построения эпюры нормальных напряжений, с учётом площади поперечного сечения бруса.
7. Найти значение нормальных напряжений для каждого участка нагружения.
8. Построить эпюру нормальных напряжений по найденным значениям.
9. Определить опасный участок.
10. Сравнить расчётное напряжение с допустимым напряжением.
11. Сделать вывод о прочности бруса.
Пример расчета:
Для стального ступенчатого бруса нагруженного осевыми внешними силами F1 = 25 кН и F2 = 60 кН при площадях поперечных сечений A1 = 500 см2, A2 = 1000 см2 определить продольные силы и напряжения. Построить эпюры продольных сил и нормальных напряжений. Проверьте прочность бруса, если если [σ] = 160МПа
Решение:
1. Два участка нагружения для продольной силы:
участок 1: N1 = + 25 кН; растянут;
участок 2: 25 – 60 + N2 = 0; N2 = — 35 кН; сжат.
2. Три участка нагружения по напряжениям:
= =
= =
= =
3. На опасном участке напряжение <[ 160МПа, значит прочность бруса обеспечена.

Данные для выполнения практической работы
Параметр | Вариант | |||||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
F1, кН | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 12 | 14 | 15 | 22 | 24 | 26 | 28 | 8 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
F2, кН | 40 | 12 | 14 | 15 | 22 | 24 | 26 | 45 | 42 | 10 | 15 | 20 | 25 | 30 | 12 | 14 | 15 | 22 | 24 | 26 | 28 | 8 | 10 | 14 | 15 | 16 | 18 | 19 | 20 | 21 |
А1, см2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 2 | 4 | 6 | 8 | 10 | 12 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 3 | 6 | 9 | 15 |
А2, см2 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 2 | 18 | 16 | 14 | 12 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 2 | 4 | 6 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Вариант 1, 11, 21 | Вариант 2, 12, 22 | Вариант 3, 13, 23 | Вариант 4, 14, 24 | Вариант 5, 15, 25 | Вариант 6, 16, 26 | Вариант 7, 17, 27 | Вариант 8, 18, 28 |
|
|
|
|
|
|
|
|
Вариант 9, 19, 29 | Вариант 10, 20, 30 |
|
|
Контрольные вопросы:
| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 |
Подпишитесь на рассылку:

Смотрите полные списки:
 Профессии
Профессии
Проекты по теме:
Источник
Цель:
Для заданного ступенчатого бруса
построить эпюры продольных сил и
нормальных напряжений, определить
удлинение (укорочение) бруса, выполнить
проверочный расчет по прочности.
Задача.
Стальной двухступенчатый брус, длины
ступеней которого указаны на рис.1 (схемы
1-10), нагружен силами F1,
F2и
F3.
Построить эпюры продольных сил и
нормальных напряжений по длине бруса.
Определить перемещение свободного
конца бруса, приняв Е=2ּ105
МПа.
Числовые значения сил F1,
F2
и F3,
площади поперечных сечений ступеней
А1
и А2
для своего варианта взять из таблицы.
Таблица
Вариант | № схемы | F1 | F2 | F3 | А1 | А2 | Вариант | № схемы | F1 | F2 | F3 | А1 | А2 | |||||
кН | см2 | кН | см2 | |||||||||||||||
1 | 2 | 20 | 8 | 14 | 1,2 | 1,8 | 18 | 10 | 19 | 11 | 34 | 1,3 | 0,9 | |||||
2 | 3 | 16 | 25 | 28 | 1,2 | 1,8 | 19 | 9 | 31 | 46 | 20 | 1,9 | 2,5 | |||||
3 | 4 | 26 | 9 | 10 | 1,9 | 1,6 | 20 | 2 | 18 | 10 | 15 | 1,2 | 1,8 | |||||
4 | 6 | 28 | 22 | 12 | 2,8 | 2,6 | 21 | 1 | 16 | 15 | 10 | 1,1 | 1,8 | |||||
5 | 5 | 14 | 16 | 10 | 2,1 | 1,9 | 22 | 4 | 24 | 10 | 8 | 2,0 | 0,7 | |||||
6 | 8 | 10 | 12 | 13 | 0,9 | 0,7 | 23 | 3 | 15 | 24 | 29 | 1,3 | 2,9 | |||||
7 | 7 | 17 | 13 | 6 | 1,1 | 1,5 | 24 | 6 | 26 | 20 | 10 | 2,6 | 2,2 | |||||
8 | 10 | 29 | 2 | 54 | 1,9 | 1,4 | 25 | 5 | 20 | 18 | 12 | 2,5 | 2,2 | |||||
9 | 9 | 40 | 55 | 24 | 2,8 | 3,4 | 26 | 8 | 9 | 11 | 12 | 1,9 | 0,8 | |||||
10 | 2 | 15 | 5 | 13 | 1,0 | 1,2 | 27 | 7 | 14 | 10 | 6 | 1,1 | 1,3 | |||||
11 | 1 | 30 | 10 | 5 | 1,8 | 2,6 | 28 | 10 | 30 | 4 | 56 | 2,0 | 1,5 | |||||
12 | 3 | 8 | 13 | 14,5 | 0,6 | 1,2 | 29 | 9 | 25 | 41 | 18 | 1,6 | 2,1 | |||||
13 | 4 | 16 | 6 | 2 | 1,0 | 0,7 | 30 | 2 | 11 | 6 | 12 | 0,8 | 1,2 | |||||
14 | 6 | 19 | 14 | 4 | 2,4 | 2,1 | 31 | 1 | 17 | 13 | 8 | 1,0 | 2,1 | |||||
15 | 5 | 17 | 19 | 13 | 2,4 | 2,1 | 32 | 3 | 18 | 25 | 7 | 1,5 | 3,2 | |||||
16 | 8 | 17 | 19 | 20 | 1,6 | 1,4 | 33 | 4 | 32 | 17 | 2 | 3,0 | 1,5 | |||||
17 | 7 | 20 | 17 | 10 | 1,3 | 1,9 | 34 | 5 | 19 | 8 | 22 | 2,1 | 1,8 | |||||
Лабораторная работа №2 «Испытание на растяжение образца из низкоуглеродистой стали».
Цель
работы:
Изучение поведения стального образца
при растяжении до разрушения. Определение
величин основных механических
характеристик материала.
Оборудование:
разрывная машина УММ-5, образец.
Порядок выполнения и оформления работы
Изучить
и законспектировать
тип, наименование, принцип действия и
устройство испытательной машины.Зарисовать
эскиз образца до и после испытания.
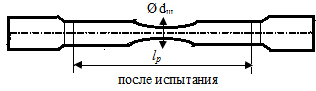
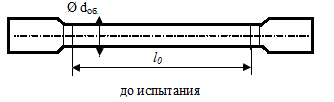
Записать
размеры образца,
данные своего варианта взять из таблицы
1 и схемы и занести в таблицу 2.
Таблица
1. Данные варианта.
Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
№ схемы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Вариант | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
№ схемы | 11 | 12 | 13 | 14 | 15 | 1 | 2 | 3 | 4 | 5 |
Вариант | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
№ схемы | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Таблица
2 Размеры образца
До | После |
Диаметр | Диаметр |
Расчетная | Удлинение |
Площадь | Расчетная |
Площадь |
Вычислить
результаты работы:
Нагрузка,
соответствующая пределу пропорциональности
Fпц=Нагрузка,
соответствующая пределу текучести Fт=Нагрузка,
соответствующая пределу прочности
Fnр=
Результаты
испытаний
Предел
пропорциональности σпц=Предел
текучести σт=Предел
прочности σnр=Относительное
удлинение δ=Относительное
остаточное сужение ψ=
Вывод:
Схема
1
Размеры
образца до испытания:
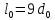 ,
,
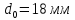 ;
;
Размеры
образца после испытания:
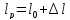 ,
,
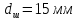 .
.
Масштаб:
по
силе «F»
1 мм=600 Н ,
по
удлинению «
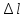 »
»
1 мм=0,005 мм
Схема
2
Размеры
образца до испытания:
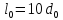 ,
,
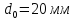 ;
;
Размеры
образца после испытания:
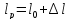 ,
,
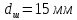 .
.
Масштаб:
по
силе «F»
1 мм=350 Н ,
по
удлинению «
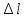 »
»
1 мм=0,02 мм
Схема
3
Размеры
образца до испытания:
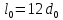 ,
,
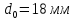 ;
;
Размеры
образца после испытания:
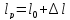 ,
,
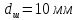 .
.
Масштаб:
по
силе «F»
1 мм=550 Н ,
по
удлинению «
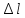 »
»
1 мм=0,0015 мм
Схема
4
Размеры
образца до испытания:
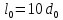 ,
,
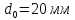 ;
;
Размеры
образца после испытания:
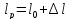 ,
,
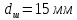 .
.
Масштаб:
по
силе «F»
1 мм=500 Н ,
по
удлинению «
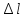 »
»
1 мм=0,0025 мм
Схема
5
Размеры
образца до испытания:
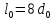 ,
,
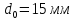 ;
;
Размеры
образца после испытания:
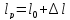 ,
,
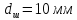 .
.
Масштаб:
по
силе «F»
1 мм=500 Н ,
по
удлинению «
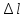 »
»
1 мм=0,004 мм
Схема
6
Размеры
образца до испытания:
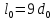 ,
,
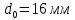 ;
;
Размеры
образца после испытания:
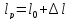 ,
,
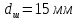 .
.
Масштаб:
по
силе «F»
1 мм=400 Н ,
по
удлинению «
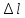 »
»
1 мм=0,0015 мм
Схема
7
Размеры
образца до испытания:
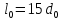 ,
,
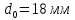 ;
;
Размеры
образца после испытания:
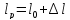 ,
,
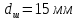 .
.
Масштаб:
по
силе «F»
1 мм=250 Н ,
по
удлинению «
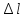 »
»
1 мм=0,005 мм
Схема
8
Размеры
образца до испытания:
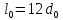 ,
,
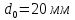 ;
;
Размеры
образца после испытания:
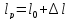 ,
,
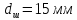 .
.
Масштаб:
по
силе «F»
1 мм=500 Н ,
по
удлинению «
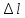 »
»
1 мм=0,003 мм
Схема
9
Размеры
образца до испытания:
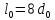 ,
,
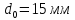 ;
;
Размеры
образца после испытания:
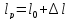 ,
,
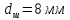 .
.
Масштаб:
по
силе «F»
1 мм=450 Н ,
по
удлинению «