Расчет элементов при центральном растяжении древесины
Как уже отмечалось, на работу древесины при растяжении существенно влияет наличие естественных пороков древесины (сучки, косослой и др.), поэтому для растянутых элементов рекомендуется применять древесину 1-го и 2-го сортов.
Расчет прочности центрально-растянутых деревянных элементов выполняется по формуле (5.1, в) (здесь и далее в расчетах центрально-растянутых деревянных элементов сохранены обозначения, принятые в СНиП 11-25-80):

где N — расчетная продольная сила; Fm — площадь поперечного сечения элемента нетто; Rp — расчетное сопротивление древесины растяжению вдоль волокон (принимается с коэффициентами условия работы тг значения которых определяются в соответствии с указаниями п. 3.2 СНиП И-25-80; так, при наличии ослаблений в расчетном сечении растянутых элементов следует учитывать коэффициент условия работы т0 = 0,8).
При определении площади нетто в растянутых деревянных конструкциях принимается во внимание, что при их разрушении линия разрыва может проходить через ослабления, расположенные не в одной плоскости. Поэтому ослабления, расположенные на длине 200 мм, суммируются (рис. 6.2).

Рис. 6.2. К определению площади нетто:
FHT — площадь сечения элемента нетто; Рослабл — площадь ослаблений
Нормы ограничивают гибкость центрально-растянутых деревянных элементов и отдельных ветвей. Предельные гибкости принимаются в соответствии с табл. 14СНиП П-25-80. Так, например, для растянутых элементов ферм в вертикальной плоскости предельная гибкость А,тах = 150, для прочих растянутых элементов ферм и других сквозных конструкций А,тах = 200.
Проверка гибкости выполняется по формуле (5.3, в):

где /0 — расчетная длина элемента; г — радиус инерции сечения; ^шах — предельная гибкость.
Порядок расчета центрально-растянутого деревянного элемента (тип 1)
- 1. Принимают древесину и ее сорт; определяют расчетное сопротивление растяжению вдоль волокон (для древесины сосны, ели) Rp (табл. 2.4); в случае если элемент выполнен из древесины других пород, расчетное сопротивление умножают на переходной коэффициент тп (табл. 2.5).
- 2. Определяют коэффициенты условия работы в соответствии с указаниями п. 3.2 СНиП И-25-80 (так, при наличии отверстий, врезок следует учитывать коэффициент условия работы т0 = 0,8).
- 3. Определяют требуемую площадь сечения нетто FTTpe6:

- • если элемент не имеет ослаблений (отверстий, врезок), площади сечения брутто и нетто равны, F- Fm;
- • если в элементе имеются ослабления, необходимо требуемую площадь сечения определять как сумму требуемой площади нетто и площади ослабления (величину ослабления назначают, предварительно задавшись толщиной элемента, впоследствии возможна корректировка принятых размеров).
- 4. По требуемой площади подбирают сечение элемента и определяют фактические значения площадей брутто, нетто, значения радиусов инерции сечения.
- 5. Выполняют проверку подобранного сечения:
- • проверяют гибкость: X = — ?1макс;
г
N
• проверяют прочность: о = — ILm .
F у
1 нт
Задача 2-го типа — проверка прочности центрально-растянутого элемента является частью задачи 1-го типа (выполнение п. 5 порядка расчета).
Примеры расчета центрально-растянутых элементов
Пример 6.1. Подобрать сечение стальной подвески, выполненной из листовой стали (рис. 6.3). Подвеска центрально-растянута силой N= 200 кН; уп= 1,0.
Решение
1. Принимаем сталь С 245; устанавливаем расчетное сопротивление стали по пределу текучести Ry = 240 МПа = 24 кН/см2 (табл. 2.2).

Рис. 6.3. К примеру 6.1
- 2. Устанавливаем величину коэффициента условия работы: ус = = 0,9 (табл. 2.3).
- 3. Определяем требуемую площадь сечения нетто Ап:

4. Принимаем толщину листа, из которого выполняется подвеска, и определяем площадь ослабления:

5. Определяем требуемую площадь сечения с учетом площади, занятой ослаблением:

6. Определяем требуемую ширину подвески и назначаем ее сечение:

принимаем сечение подвески 8 х 160 мм.
7. Проверяем прочность; для этого предварительно определяем фактическое значение площади сечения нетто:

прочность сечения обеспечена; нормами гибкость подвески не ограничивается (см. табл. 20 СНиП 11-23-81*).
Вывод. Принимаем сечение подвески 8 х 160 мм из стали С245.

Рис. Б.4. К примеру 6.2. Крепление затяжки к поясу фермы
Пример 6.2. Проверить прочность и гибкость центрально-растянутой деревянной затяжки треугольной безраскосной фермы, выполненной из доски сечением 50 х 125 мм, которая прикреплена к верхнему поясу стропильной фермы болтом d = 12 мм и четырьмя гвоздями d= 5 мм, /=150 мм (рис. 6.4). Древесина — сосна, сорт 1. Усилие в затяжке N= 34,0 кН; уп = 0,95. Расчетная длина /0 = 2,5 м. Условия эксплуатации фермы Б2.
Решение
1. Находим усилие в затяжке с учетом коэффициента надежности по ответственности уп:

2. Определяем расчетное сопротивление древесины растяжению вдоль волокон:

3. Определяем коэффициенты условий работы:

4. Находим площадь сечения нетто:

5. Проверяем прочность затяжки:

прочность обеспечена.
6. Определяем радиусы инерции затяжки (табл. 5.2):
/

7. В соответствии с табл. 14 СНиП П-25-80 для прочих растянутых элементов ферм (к которым относится затяжка) предельная гибкость А,тах = 200. Проверяем гибкость затяжки:

Вывод. Прочность и гибкость затяжки отвечают требованиям норм.
Задачи для самостоятельной работы
Задача 6.1. Проверить прочность и гибкость стального центрально-растянутого стержня круглого сечения (рис. 6.5). Растягивающая сила N= 30 кН, уп = 0,9. Сталь С345; ус = 0,95. Расчетная длина стержня lef = 1000 мм. Предельная гибкость А,пред = 400.

Рис. 6.5. К задаче 6.1
Задача 6.2. Подобрать сечение центрально-растянутого нижнего пояса деревянной фермы. Материал: брус, сосна, сорт 2. Условия эксплуатации Б2 (тв = 1,0). В нижнем поясе имеется ослабление за счет врезки (т0 = 0,8) глубиной Авр = 4 см (рис. 6.6). На нижний пояс действует растягивающая сила 7V= 200 кН; уп = 0,95. Расчетная длина /0 = 3,0 м. СНиП Н-25-80 ограничивает предельную гибкость растянутых поясов в вертикальной плоскости А,тах = 150.

Рис. 6.6. К задаче 6.2
Источник
2.1. Особенности работы древесины на растяжение вдоль волокон
Для
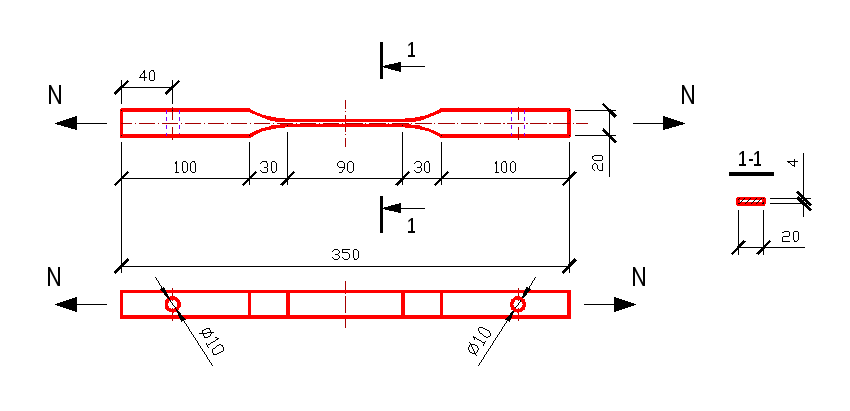
получения прочностных характеристик
древесины на растяжение испытываются
малые образцы следующей формы (см. рис
ниже).
Для сосны и ели
при влажности 12% максимальный предел
прочности чистой древесины на растяжение
вдоль волокон достигает 200 МПа.
Прочность
древесины реальных элементов конструкций
резко снижается за счет неоднородности
строения древесины. Особенно опасны
при растяжении сучки на кромках с выходом
на ребро и наличие косослоя. Сучки
являются концентраторами напряжений.
При косослое растягивающее усилие
раскладывается на две составляющие
вдоль наклонно расположенных волокон
и перпендикулярно к ним. Это вызывает
растяжение поперек волокон, скалывание
и сдвиг. Допускаемый косослой лежит в
пределах
![]() на
на![]() длины элемента.
длины элемента.
С
учетом приведенных выше факторов
коэффициент однородности древесины
при растяжении принимается 0,275, а
расчетное сопротивление на растяжение
составляет для первого сорта всего
![]() — для не клееных элементов и
— для не клееных элементов и![]() — для клееных элементов.
— для клееных элементов.
П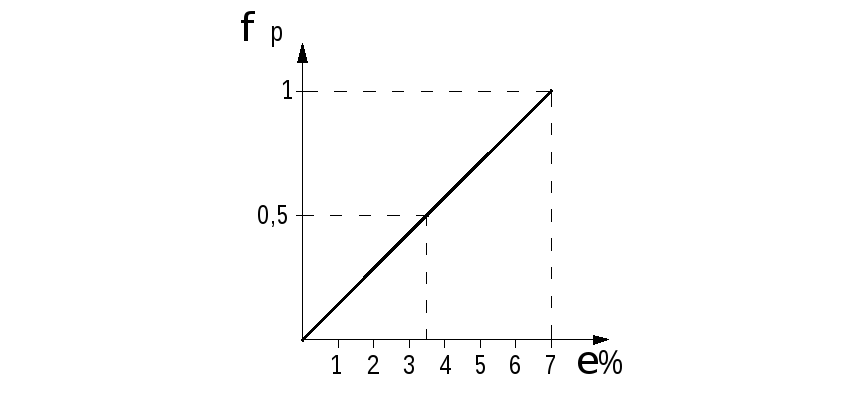 риведенная
риведенная
диаграмма работы древесины на растяжение
вдоль волокон имеет незначительную
кривизну (![]() относительное напряжение, выраженное
относительное напряжение, выраженное
в долях от предельной прочности), примерно
посередине диаграммы происходит
отклонение от первоначального направления,
т.е.![]() является пределом пропорциональности.
является пределом пропорциональности.
Деформации возрастают прямо пропорционально
напряжениям почти до момента разрушения,
которое происходит при очень малых
деформациях — всего 0,7% от первоначальной
длины. Разрушение растянутых элементов
происходит хрупко по пилообразной
поверхности.
Предел
прочности древесины на растяжение
поперек волокон в 12… 17 раз меньше, чем
при растяжении вдоль волокон вследствие
анизотропии строения древесины.
На
центральное растяжение работают нижние
пояса и растянутые раскосы ферм при
узловой нагрузке, затяжки арок и другие
элементы.
Расчет центрально растянутых элементов
Расчет
центрально-растянутых элементов
производится по формуле
![]() ,
,
где
![]() расчетная продольная сила;
расчетная продольная сила;![]() расчетное сопротивление древесины
расчетное сопротивление древесины
растяжению вдоль волокон, определенное
с учетом всех необходимых коэффициентов
условий работы;![]() площадь нетто поперечного сечения
площадь нетто поперечного сечения
элемента;![]() учитывает концентрацию напряжений,
учитывает концентрацию напряжений,
которая возникает в местах ослаблений.
Рассмотрим
предпосылки к определению
![]() .
.
Было замечено, что при ослаблении
деревянных элементов отверстиями и
врезками их прочность, в некоторых
случаях, снижается больше, чем получается
по площади нетто. Это происходит из-за
концентрации напряжений вокруг
ослаблений.
1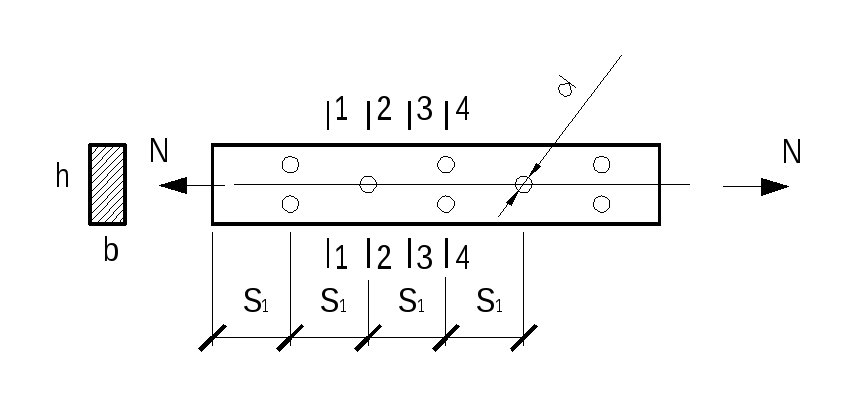 -1
-1
все волокна загружены одинаково; 2-2 —
часть волокон без ослабления нагружены
сильнее; 3-3 — волокна нагружены неравномерно,
однако на расстоянии
![]() напряжения будут выравниваться, если
напряжения будут выравниваться, если
расстояние достаточно велико, если нет,
то 4-4 — два ослабления: соседние волокна
получают дополнительные напряжения,
что может привести к достижению ими
предела пропорциональности.
Поэтому
при определении площади
![]()
ослабления,
расположенные по длине элемента на
расстоянии друг от друга менее 200 мм,
принимаются совмещенными в одном сечении
из-за неравномерности распределения
растягивающих напряжений в расчетном
сечении (опасности разрыва волокон «по
зигзагу»).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
На работу и прочность растянутых элементов оказывают очень неблагоприятное влияние неизбежные в них ослабления и такие пороки древесины, как сучки, косослой и трещины. В нормах это обстоятельство учтено снижением допускаемого напряжения растяжения по сравнению с изгибом и сжатием до [σр] = 70 кг/см2, хотя лабораторные образцы показывают значительно большую прочность при растяжении, чем при изгибе и сжатии. Кроме того, для изготовления растянутых и растянуто-изгибаемых элементов деревянных конструкций необходимо применять наилучший лесоматериал, с наименьшим количеством дефектов, удовлетворяющий качественным требованиям, предъявляемым к элементам первой категории.
Расчет центрально растянутых деревянных стержней заключается в проверке напряжений с учетом имеющихся ослаблений сечения.
Распределение растягивающих напряжений по сечению стержня принимают равномерным. Напряжение в наиболее ослабленном сечении растянутого элемента проверяют по ф-е: σр =Np/Fнт≤[σр]
где N р – растягивающая сила; Fнт – площадь поперечного сечения нетто за вычетом всех ослаблений.
Расстояние между отверстиями для болтов S = 10 < 20 см, следовательно, учитываем ослабления всеми тремя отверстиями, считая их совмещенными в одном сечении.
Расчетная площадь нетто: Fнт = Fбр – (F′осл + F″осл )
Напряжение растяжения:
σр =Np/Fнт=69,5 < 70 кг,см2
Сжатие вдоль волокон
Должно быть выполнено следующее условие: סс,0,d =ס fс,0,d,
Для элементов с гибкостью ס следует также провести проверку на устойчивость סс,0,d =ס kcfс,0,d,
Гибкость элементов цельного, постоянного по длине сечения определяется по формуле λ=ld/i, где ld — расчетная длина элемента; i — радиус инерции сечения элемента в направлении соответствующей оси. Расчетную длину элемента (ld) следует определять умножением его свободной длины (l) на коэффициент (m0), учитывающий закрепление элемента и нагрузку, действующую на элемент ld = m0l . Коэффициент (m0) следует принимать по таблице 7.1. Расчетную длину пересекающихся элементов, соединенных между собой в месте пересечения, следует принимать равной:
а) при проверке устойчивости в плоскости конструкции — расстоянию от центра узла до точки пересечения элементов;
б) при проверке устойчивости из плоскости конструкции:
— в случае пересечения двух сжатых элементов — полной длине элемента; — в случае пересечения сжатого элемента с неработающим — величине (l1), умноженной на коэффициент (m0):
Величину (m0) следует принимать не менее 0,5; — в случае пересечения сжатого элемента с растянутым равной по величине силой — наибольшей длине сжатого элемента, измеряемой от центра узла до точки пересечения элементов.
Гибкость элементов переменного сечения (ס следует определять с учетом отношения соответствующей жесткости эквивалентного стержня к жесткости стержня в расчетном сечении.
95. Поперечный изгиб
При изгибе должно удовлетворяться следующее условие (ym,y,d/fm,y,d)+ (ym,z,d/fm,z,d)≤1, где fm,y,d и fm,z,d — соответствующие значения расчетных сопротивлений изгибу; סm,y,d и סm,z,d — расчетные напряжения изгиба относительно заданной оси, определяемые по формуле:
סm,i,d = Mi,d/Wi,d , где Mi,d — расчетный изгибающий момент относительно соответствующей оси; Wi,d — расчетный момент сопротивления поперечного сечения элемента относительно соответствующей оси и принимаемый для цельных элементов Wi,d = Wi,inf. При определении (Wi,inf) ослабления сечений, расположенные на участке элемента до 0,2 м, принимать совмещенными в одном сечении. Для изгибаемых элементов, не имеющих постоянного подкрепления сжатой кромки из плоскости изгиба, следует также провести проверку на устойчивость плоской формы деформировании
סm,d =kinst fm,d ,где kinst — коэффициент устойчивости изгибаемого элемента. Для изгибаемых элементов прямоугольного постоянного сечения, шарнирно закрепленных от смещения из плоскости изгиба и закрепленных от поворота вокруг продольной оси в опорных сечениях, (kinst) определяется по формуле kinst=140*kf* b2/lmh
где lm — расстояние между опорными сечениями элемента, а при закреплении сжатой кромки элемента в промежуточных точках от смещения из плоскости изгиба — расстояние между этими точками;
b — ширина поперечного сечения; h — максимальная высота поперечного сечения на участке (lm); kf — коэффициент, зависящий от формы эпюры изгибающих моментов на участке (lm).
При проверке устойчивости изгибаемых элементов с линейно меняющейся по длине высотой и постоянной шириной, не имеющих закреплений из плоскости по растянутой кромке, коэффициент (kinst) следует умножать на дополнительный коэффициент (kg,m),
97. Изгиб с осевым сжатием
При изгибе с осевым сжатием должно удовлетворяться следующее условие (yc,0,d/fc,0,d)+ (ym,y,d/ km,c,y fm,y,d)+ (ym,z,d/ km,c,z fm,z,d) ≤1, где סc,0,d — расчетное напряжение сжатия
fc,0,d — расчетное сопротивление сжатию; סm,y,d, סm,z,d — расчетные напряжения изгиба
km,c — коэффициент, учитывающий увеличение напряжений при изгибе по направлению соответствующей оси от действия продольной силы.
Для шарнирно-опертых элементов при симметричных эпюрах изгибающих моментов синусоидального, параболического, полигонального и близких к ним очертаний (km,c) определяется по формуле km,c=1- yc,0,d/ kc fc,,d, где kc — коэффициент продольного изгиба,); סс,0,d — расчетное сжимающее напряжение, סс,0,d = Nd/Asup .
В случаях, когда в шарнирно-опертых элементах эпюра изгибающих моментов имеет треугольное или прямоугольное очертание, коэффициент (km,c), определяемый по формуле следует умножать на поправочный коэффициент (ke), определяемый по формуле ke = ס + km,c(1 — α), где α — коэффициент, который следует принимать равным 1,22 при эпюре треугольного очертания, и 0,81 —при эпюре прямоугольного очертания.
При значениях расчетных напряжений סm,y,d < 0,1סc,0,d и סm,z,d < 0,1סc,0,d следует дополнительно выполнить проверку на устойчивость) без учета напряжений от изгиба.
Лобовые упоры
Лобовые упоры — самые простые и надежные соединения: сжатый элемент своим торцом попросту упирается в опору. Опорой может служить каменная, бетонная кладка или другой деревянный элемент. Конец примыкающего сжатого элемента надо обрезать под прямым углом к оси. Чаще всего с помощью лобовых упоров решаются соединения двух деревянных элементов — стыки свай и стоек, узлы сопряжения стоек с насадками, узлы сопряжения подкосов с ригелем и др Лобовые врубки с одним зубом часто применяются в опорных узлах ферм построечного изготовления при небольших пролетах и нагрузках). Сжатый наклонный элемент верхнего пояса концом упирается в гнездо, выпиленное в растянутом нижнем поясе. Рабочая площадка гнезда располагается перпендикулярно направлению сжимающей силы. По нерабочей площадке устраивается клиновидный зазор (до 2—3 см на краю гнезда), так как при просадке фермы происходит поворот верхнего пояса и возможен отрыв зуба. Конец сжатого элемента опиливается так, чтобы его ось проходила точно через центр площадки смятия. Ось нижнего пояса лучше провести точно по центру сечения, ослабленного врубкой. Тогда это сечение будет только растягиваться центральной силой Np.
Источник
Растянутые элементы – это нижние пояса ферм, затяжки арок и стержни других сквозных конструкций.
Работа деревянных элементов при растяжении является наиболее ответственной и растянутые элементы надо изготовлять, как правило, из наиболее прочной древесины 1 сорта. Но при отсутствии такого материала допускается в мало напряженных элементах применять древесину 2 сорта. Прочность растянутых элементов в тех местах, где они ослаблены отверстиями или врезками, снижается в результате дополнительной концентрации напряжений у их краев. Это учитывается коэффициентом ko = 0,8 к расчетному сопротивлению древесины. Поэтому при определении ослабленной площади сечения Ainf все ослабления на этой длине суммируются, как бы совмещаются в одном сечении.
Расчет центрально-растянутыхэлементов по прочности производится по формуле:
σt,0,d= Nd/Ainf <= ft,0,d, где Nd — расчетная продольная сила; Ainf — площадь поперечного сечения элемента нетто
ft,0,d – расчетное сопротивление древесины растяжению вдоль волокон
По 2-й группе предельных состояний (по деформациям) растянутые элементы не проверяются.
Расчет сжатых элементов
На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм и других сквозных конструкций. Пороки древесины воспринимают часть сжимающих напряжений. Поэтому сжатые элементы рекомендуется изготовлять из древесины II сорта.
Расчет центрально-сжатых элементовпроизводится по формуле на прочность σс,0,d <= fс,0,d,
σс,0,d <= kcfс,0,d, где σс,0,d = Nd/Ad
Ad — расчетная площадь поперечного сечения, принимаемая равной:
— площади сечения брутто (Asup), если ослабления не выходят на кромки и площадь ослабления не превышает 25 %;
— площади сечения нетто (Ainf), с коэффициентом 4/3, если ослабления не выходят на кромки и площадь ослабления превышает 25 %;
— площади сечения нетто (Ainf), если ослабления выходят на кромки;
kc — коэффициент продольного изгиба, определяемый в зависимости от гибкости элемента. kc=1-с() при ,с=0,8 ,
kc= при ,С=3000
Гибкость элементов цельного, постоянного по длине сечения определяется по формуле где ld — расчетная длина элемента;i — радиус инерции сечения элемента в направлении соответствующей оси. Расчетную длину элемента (ld) следует определять умножением его свободной длины (l) на коэффициент (m0), учитывающий закрепление элемента и нагрузку, действующую на элемент ld = m0l . Коэффициент (m0) следует принимать по таблице СНБ.
Изгибаемые элементы – это балки, настилы, обшивки.
Изгибаемые элементы, изготавливаются из древесины 2 сорта, в малоответственных элементах можно использовать древесину 3 сорта, т. к. они работают надежно и предупреждают об опасности разрушения заранее большими прогибами. Расчет изгибаемых элементов, устойчивость которых обеспечена, производится по формуле::,где fm,,d — соответствующие значения расчетных сопротивлений изгибу;Md — расчетный изгибающий момент относительно соответствующей оси; Wd — расчетный момент сопротивления поперечного сечения элемента относительно соответствующей оси и принимаемый для цельных элементов Wd = Winf. При определении (Winf) ослабления сечений, расположенные на участке элемента до 0,2 м, принимать совмещенными в одном сечении. Для изгибаемых элементов, не имеющих постоянного подкрепления сжатой кромки из плоскости изгиба, следует также провести проверку на устойчивость плоской формы деформирования: , где Mmax — максимальный изгибающий момент на рассматриваемом участке lm; Wsup —момент сопротивления брутто на том же участке, kinst — коэффициент устойчивости изгибаемого элемента.Для изгибаемых элементов прямоугольного постоянного сечения, шарнирно закрепленных от смещения из плоскости изгиба и закрепленных от поворота вокруг продольной оси в опорных сечениях, (kinst) определяется по ф-ле: ,где lm — расстояние между опорными сечениями элемента, а при закреплении сжатой кромки элемента в промежуточных точках от смещения из плоскости изгиба — расстояние между этими точками; b — ширина поперечного сечения;
h — максимальная высота поперечного сечения на участке (lm);
kf — коэффициент, зависящий от формы эпюры изгибающих моментов на участке (lm), определяемый по таблице СНБ.
Источник
