Продольная сила при растяжении
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
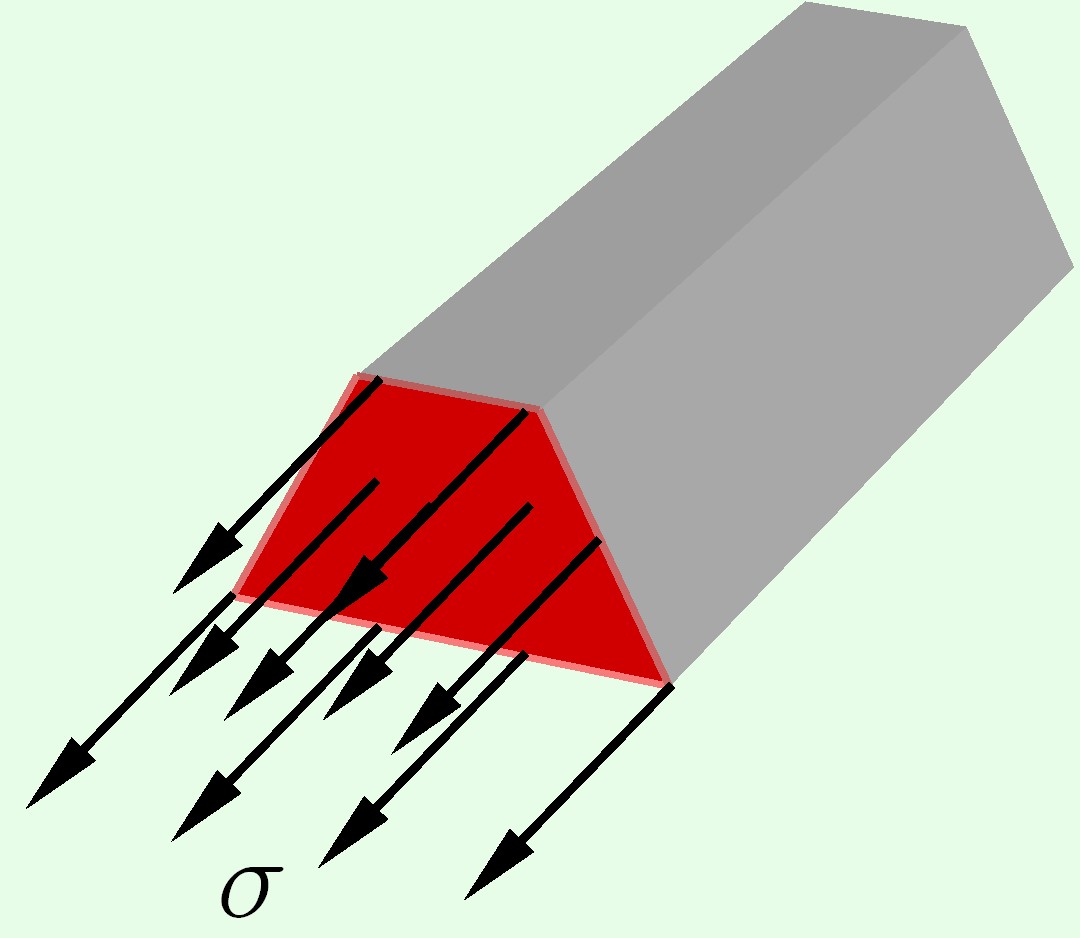
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Растяжением или сжатием называется такой вид деформаций, при котором в любом поперечном сечений бруса возникают только продольная сила . Брусья с примолинейной осью называют стержнями (рис.1).
Рис. 35.
Примой брус постоянного поперечного сечения , длиной , жестко защемленный одним концом и нагруженный на другом конце растягивающей силой F (рис.35). Под действием этой силы, брус удлинится на некоторою величину которую назовем абсолютным удлинением. Отношение абсолютного удлинения к первоначальной длине назовем относительным удлинением и обозначим .
При расчете, мы будем считать, что растяжение и сжатие бруса связано только с приложенными внешними силами, то есть учитываем только напряжения, действующие на стержень, температуру и время действий сил не будем учитывать.
При растяжении и сжатии продольные силы определяется методом сечении. Правило знаков будем определять следующим образом: растягивающие, то есть, направленные от сечения, продольные силы будем считать положительными, сжимающие, то есть направленные к сечению, будем считать отрицательными.
Для наглядного изображения распределения вдоль оси бруса продольных сил и нормальных напряжений строят графики, называемые эпюрами, причем для нормальных напряжений применяется то же правило знаков, что и для продольных сил.
При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле:
площать поперечного сечения бруса,
Очевидно, что при растяжении и сжатии форма сечения на напряжения не влияет.
Условие прочности бруса при растяжении и сжатии определяется следующим образом:
Здесь называют допускаемым напряжением, максимальная продольная сила.
Напряжения и деформаций при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Гоберта Гука. Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению бруса.
Математически закон Гука можно вписать в виде равенства:
Коэффициент пропорциональности Е характеризует жесткость материала и называется модулем продольной упругости. Модуль упругости и напряжения выражаются в одинаковых единицах.
Если в формулу закона Гука поставим выражения и то получим:
Контрольные вопросы
1. Что такое растяжение-сжатие?
____
2. По какому методу определяется нормальные силы?
__
3. По какой формуле определяется относительное удлинение или укорочение?
____
4. Какое напряжение появляется при растяжении-сжатии, и по какой формуле определяется?
____
5. Как пишется условие прочности при растяжении-сжатии?
____
6. Что такое модуль упругости, и в чем измеряется?
____
7. От чего зависит модуль упругости?
__
8. По какой формуле определяется абсолютное удлинение или укорочение бруса при растяжении-сжатии?
____
Пример 4.1.
Для данного ступенчатого бруса (рис.36.) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если .
Рис.36.
1. Разбиваем брус на участки как показоно на рис. 37а.
Рис.37.
2. По методу сечения определяем ординаты эпюр и каждого сечения.
4. Строим эпюру (рис. 37б.)
5. Определяем перемещение свободного конца бруса.
Пример 4.2.
Для данного ступенчатого бруса (рис.38.) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если .
Рис. 38.
1. Разбиваем брус на участки как показоно на рис. 39а.
2. По методу сечения определяем ординаты эпюр и каждого сечения.
Рис. 39.
3. Строим эпюру (рис. 37б.)
4. Определяем перемещение свободного конца бруса.
Для решения первой задачи контрольной работы 2 следует выполнить следующие действия:
1) Изучить темы 7,8,9.
2) Ответить на контрольные вопросы по темам 7,8,9.
2) Выполнить самостоятельно пример 2.2.
Данные для своего варианта первой задачи контрольной работы 2 посмотрите в таблице 4. Расчетную схему надо посмотреть в рис.40.
Таблица 4 (для первой задачи контрольной работы 2)
| Номер варианта | Номер схемы на рис. 40. | ||
| кН | |||
| I | 3,6 | 1,4 | |
| II | 2,4 | 1,1 | |
| III | 3,5 | 2,5 | |
| IV | 2,9 | 1,4 | |
| V | 1,9 | 1,1 | |
| VI | 3,7 | 2,3 | |
| VII | 4,4 | 2,6 | |
| VIII | 4,6 | 3,1 | |
| IX | 4,2 | 3,2 | |
| X | 3,1 | 1,5 | |
| I | 3,6 | 2,4 | |
| III | 3,5 | 2,5 | |
| V | 2,8 | 1,2 | |
| VII | 3,0 | 2,2 | |
| II | 2,8 | 1,4 | |
| IV | 2,4 | 1,2 | |
| VI | 3,6 | 2,6 | |
| IX | 2,1 | 1,0 | |
| VIII | 2,6 | 1,3 | |
| X | 3,8 | 1,6 | |
| V | 1,4 | 3,2 | 1,8 |
| III | 3,4 | 1,5 | |
| VII | 2,3 | 2,9 | 1,9 |
| VIII | 3,6 | 1,7 | |
| II | 2,9 | 1,6 | |
| I | 3,4 | 2,1 | |
| III | 3,5 | 2,4 | |
| V | 3,6 | 2,3 | |
| VII | 3,2 | 2,2 | |
| II | 3,6 | 2,6 |
Рис. 40.
Источник
Внутренние силы при растяжении-сжатии
Центральное растяжение-сжатие возникает в случае, когда на концах стержня вдоль его оси действуют две равные противоположно направленные силы. При этом в каждом сечении по длине стержня возникает внутреннее усилие (продольная сила$N$ кН), которая численно равна сумме всех сил, которые действуют вдоль оси стержня и расположены с одной стороны от сечения.

Из условий равновесия отсеченной части стержня $N = F$.
Продольная сила при растяжении считается положительной, при сжатии – отрицательной.
Пример определения внутренних сил.
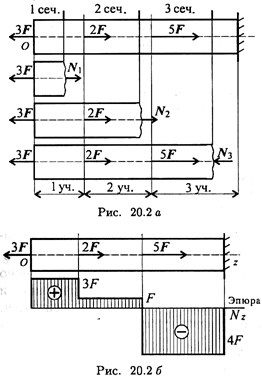
Рассмотрим брус, нагруженный внешними силами вдоль оси. Брус закреплен в стене (закрепление «заделка») (рис. 20.2а). Делим брус на участки нагружения.

Участком нагружения считают часть бруса между внешними силами.
На представленном рисунке 3 участка нагружения.
Воспользуемся методом сечений и определим внутренние силовые факторы внутри каждого участка.
Расчет начинаем со свободного конца бруса, чтобы не определять величины реакций в опорах.
Продольная сила положительна, участок 1 растянут.
Продольная сила положительна, участок 2 растянут.
Продольная сила отрицательна, участок 3 сжат.
Полученное значение N3 равно реакции в заделке.
Под схемой бруса строим эпюру продольной силы (рис. 20.2, б).
Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.
Ось эпюры параллельна продольной оси.
Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные — вверх, отрицательные — вниз.
В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Напряжения. Действующие и допускаемые напряжения
Величина внутренней силы дает представление о сопротивлении поперечного сечения в целом (интегрально), но не дает представления об интенсивности работы материала в отдельных точках сечения. Так, при равной продольной силе материал в стержне с большим сечением будет работать менее интенсивно, менее напряженно чем меньший.
Напряжения – внутренние силы, приходящиеся на единицу площади сечения. Напряжения, направленные перпендикулярно (по нормали) к сечению называются нормальными.
$sigma = frac{N}{A}$
Единицы измерения напряжений — Па, кПа, МПа.
Знаки напряжений принимают так, как и для продольной силы.
Действующие напряжения — напряжения, которые возникают в рассматриваемом сечении.
Любой стержень в момент разрушения имеет определенные напряжения, которые зависят только от материала стержня и не зависят от площади сечения.
Допускаемые напряжения $left[ sigma right]$ – такие напряжения, которые не должны быть превышены в запроектированных конструкциях. Допустимые напряжения зависят от прочности материала, характера его разрушения, степени ответственности конструкции.
Принцип Сен-Венана: в сечениях, достаточно удаленных от места приложения нагрузки, распределение напряжений не зависит от способа приложения нагрузки, а зависит только от его равнодействующей.
то есть, распределение напряжений в сечении I-I для трех различных случаев, показанных на рисунке, принимается одинаковым.
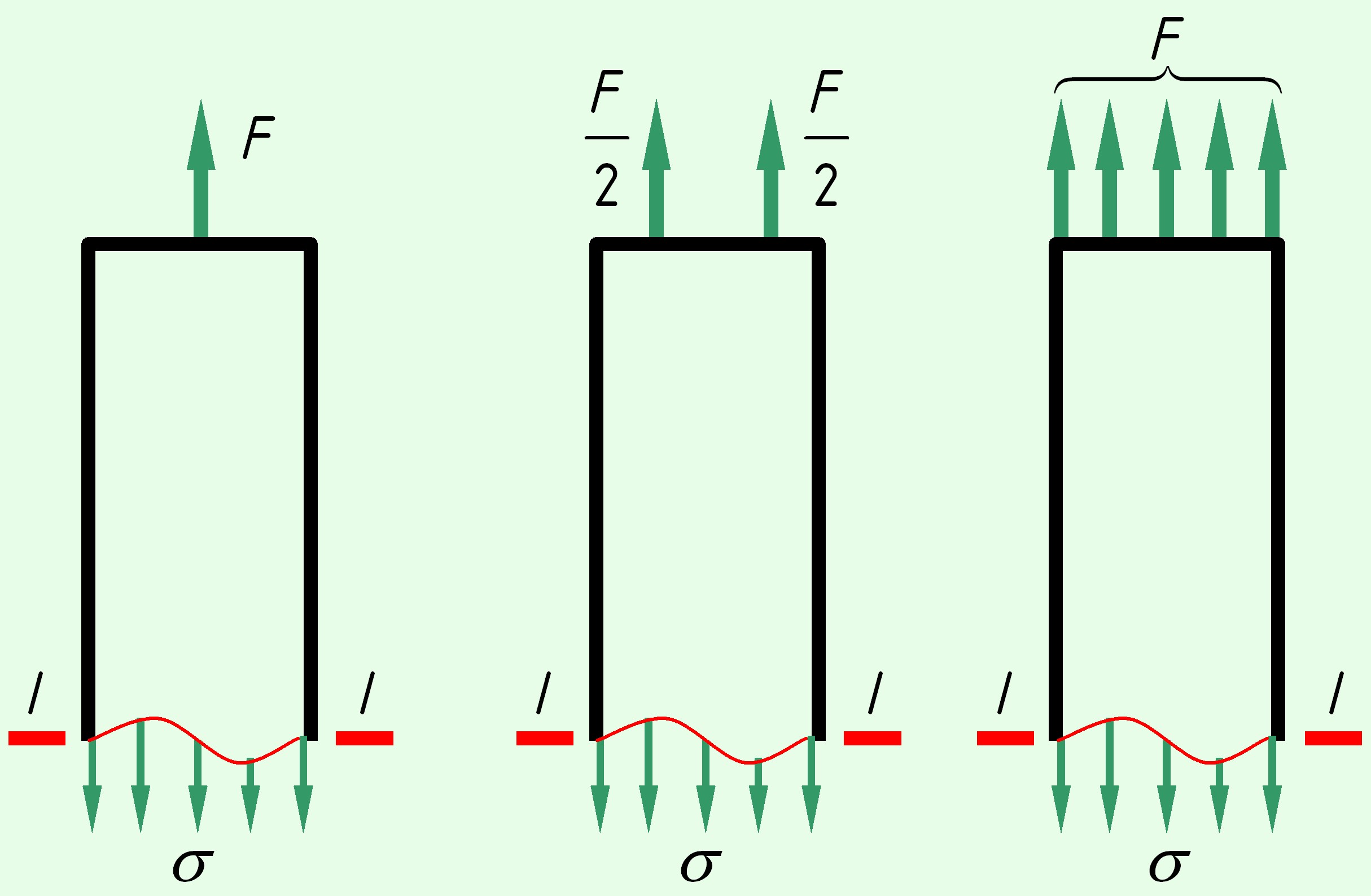
Рисунок — иллюстрация принципа Сен-Венана
Абсолютная и относительная деформация
При растяжении возникает удлинение стержня – разница между длиной стержня до и после погрузки. Эта величина называется абсолютной деформацией.
$Delta l = {l_1} — l$
Относительная деформация – отношение абсолютной деформации к первоначальной длине.
$varepsilon = frac{{Delta l}}{l}$
$sigma = E cdot varepsilon $
Таблица — физико-механические характеристики материалов
Материал | Модуль упругости, х1010 Па | Коэффициент Пуассона |
Сталь | 19 – 21 | 0,25 – 0,33 |
Чугун | 11,5 – 16 | 0,23 – 0,27 |
Медь, латунь, бронза | 10 | 0,31 – 0,42 |
Алюминий | 7 | 0,32 – 0,36 |
Кирпичная кладка | 0,3 | 0,2 |
Бетон | 1 – 3 | 0,1 – 0,17 |
Каучук | 0,0008 | 0,47 |
Источник
