При растяжении стержня длиной 70 см среднее
Анонимный вопрос
20 января 2018 · < 100
Определите ударную вязкость, если на разрушение образца была затрачена работа 110 Дж, сечение образца 5×8 мм?
https://www.youtube.com/channel/UCEyTRyMoyc7O6tYtkC_n4bA
Вычислить ударную вязкость можно по формуле ан=Ан/S.
, где Ан — работа, потраченная на деформацию и разрушение, измеряется Дж,
S — площадь поперечного сечения образца, измеряется в м2
Вычисляем площадь. 5мм*8мм = 40 мм2. В метрах это 0,040 м2.
Умножаем 110 на 0,04 и получаем 4,4.
Ударная вязкость равна 4,4 Дж/м2
Объясните чайнику: если до Большого взрыва Вселенная была бесконечно мала, то как называлось то пространство, которое ее окружало?
Так нет никакого пространства вне Вселенной. Просто ничего. Да и говорить о том что Вселенная была сжата тоже нельзя и это не правильно, т.к. Вселенную извне нечему сдерживать из вне — там вросто нет абсолютно ничего. Даже называя словами абсолютно ничего мы уже это ничего как-то материализуем, как минимум у этого ничего уже есть название. Так устроен наш мозг. А это то, что вообще не имеет даже навания, потому-что там называть нечего и даже понятия «там» нет. Это тоже самое как открыть флешку в командоре, зайти в нее и представить что существует вне места на флешке. Просто всем, чем можно вообще оперрировать с местом на флешке ограничено. А вне этого ограничения просто физически ничего нет. Вселенная расширяется до тех пор, пока последний атом не будет расщеплен на энергию. Вот стадия Вселенной когда последний атом расщипился и больше нечему расширять пространство. Большая вероятность, что Вселенная начнет тогда схлопываться, концентрируя энергию и уменьшая свой объем. До тех пор, пока концентрат энергии не приведет к образованию первых элементарных частиц (кварки, глюоны) и не запустится процесс вспять и начнутся стадии «конденсат цветного стекла», «глазма» и т.д. И так до бесконечности. Это наша Вселенная. Она так вечность делает и будет делать. А вот одна ли она и является ли она частью чего-то большго — нам пока-что не известно.
Прочитать ещё 55 ответов
Какой удар (в ньютонах) способен выдержать лист титана толщиной в 10 см? Как вычислить по ударной вязкости?
Если KCU =120 Дж/см^2 , то груз массой 500 кг, падающий с высоты 3 метров, в сечении листа 100 см^2 даст значение KCU (расчётное) равное 150 Дж/см^2.
Ну как всегда, ответил и прочёл вопрос полностью.. слишком маленький коэффициент ударной вязкости, при переводе в СИ получится значение 0,6 Нм/см^2. Ну ладно, допустим это правильн. Расчёт делается по сечению, поперечному, листа. Образцы ломают сечением 1 см^2. То есть расчёт надо делать исходя из сечения листа с учётом его толщины. Формула там простая, формула именно коэфф уд вязк
KC=А/F. A=Q*h, Нм — работа, F — площад сечения см^2
я сейчас заменю значения в таблице и сброшу ещё раз расчёт
Что то не то у тебя с коэффициентом? Груз массой 6 кг, упавший на лист титана толщиной 100 мм, с метровой высоты, даже вмятины не оставит. Коэффициент уточни
Как тело с большей массой может развить скорость больше, при свободном падении, если ускорение свободного падения действует на все тела ОДИНАКОВО?
Старший научный сотрудник ИНЭОС РАН, химик, музыкант и радиолюбитель
Понятие «ускорение свободного падения» возникает из-за того, что сила гравитации, которая действует на объект пропорциональна массе, в то же время, ускорение, которое этот объект получает, по второму закону Ньютона обратно пропорционально массе. В результате, если бы не было сопротивления воздуха, масса бы сокращалась, и мы имели бы одинаковое ускорение свободного падения для всех тел, независимо от их массы, формы и размеров. Но поскольку сопротивление воздуха присутствует, реальное изменение скорости падающего объекта описывается не только с помощью g, и зависит от формы и размеров объекта, и его массы.
Прочитать ещё 1 ответ
Источник
1.1 (Вариант 4) Конструкция состоит из двух стержней, соединенных между собой и с основанием шарнирами (рис.1). К шарнирному болту С привязан груз Р. Требуется определить внутренние усилия в стержнях и подобрать их сечение по допускаемым напряжениям на сжатие и растяжение. Величина силы Р, форма сечения и допускаемые напряжения приведены в табл.1. 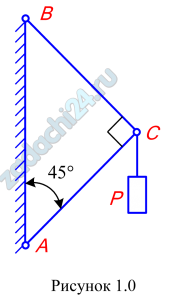
Таблица 1
| Сечение стержней | Величина Р, кН | [σ]С, МПа | [σ]Р, МПа |
 | 10 | 160 | 100 |
Ответ: NBC=7,1 кН, NAC=-7,1 кН, D=15,0 мм, d=9,0 мм.
1.2 (Вариант 29) Двухступенчатый стальной брус, длины ступеней которого указаны на рис.23 (схемы I-X) нагружены силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение (укорочение) бруса, приняв Е=2·105 МПа. Числовые значения сил F1 и F2, а также площадей поперечных сечений ступеней A1 и A2 для своего варианта взять из табл.8.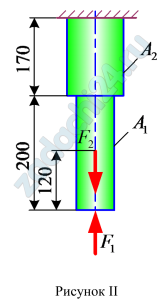
Таблица 8 — Исходные данные
| № задачи и схемы на рис.23 | F1, кН | F2, кН | А1, см2 | А2, см2 |
| 62,II | 4,8 | 10,0 | 0,4 | 0,8 |
Ответ: Δl=0,113·10-3 м.
1.3 (Вариант 2396) Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки F и при найденном значении нагрузки вычислить наибольшее перемещение бруса, а также максимальное удлинение участка a.
Принять А=200 мм², l=200 мм, s=2, остальные данные взять из табл.3.1 и табл.3.2.
Источник
1. Определение внутренних сил в растягиваемых и сжимаемых стержнях.
2. напряжения при растяжении (сжатии) прямого стержня. Понятие о допускаемом напряжении.
3. Определение деформаций и перемещений. Закон Гука.
4. Опытное изучение свойств материалов.
Растяжение и сжатие – это простой и часто встречающийся случай напряженного состояния элементов конструкции и деталей машин.
В таких условиях работает буксировочный канат или трос подъемного механизма, колонна здания.
Чистое (центральное) растяжение или сжатие возникает в элементе конструкции, если внешняя нагрузка вызывает в нем только одно внутреннее усилие, которое сопротивляется этой внешней нагрузке, — нормальную продольную силу.
При определении значений внутренних нормальных сил, действующих в поперечных сечениях стержней, примем следующее правило знаков:
— нормальная сила положительна, если сопротивляется растяжению стержня;
— нормальная сила отрицательна – если сопротивляется сжатию.
Для определения значений внутренней нормальной силы в любом из поперечных сечений используется метод сечений.
Пусть прямой стержень постоянной толщиной в одном конце закреплен, а к его другому торцу приложена растягивающая его вдоль оси стержня внешняя сила F.
Какое по величине внутреннее продольное усилие возникает в некотором поперечном сечении стержня n-n?
Прежде всего, отметим, что под действием закрепления и внешней силы стержень растягивается (деформируется), но никуда не движется, т.е. остается в равновесии.
Удобно вначале мысленно «снять» со стержня закрепление. Заменим его влияние на стержень эквивалентно действующей внешней силой. Эта сила равна реакции закрепления.
Т.е. в закреплении возникает некоторое усилие, благодаря которому верхний край стержня остается неподвижным. Это усилие называют реакцией закрепления на внешнюю нагрузку, передающееся на это закрепление через деформируемый стержень.
Незакрепленный стержень, теперь уже под действием двух внешних воздействий: известной силы и неизвестной пока реакции также никуда не движется, т.е. находится в равновесии.
Определить величину реакции поможет математическая формулировка этого факта.
Проведем координатную ось Оz, для удобства совпадающую с осью стержня. Стержень никуда не движется под действием силы и реакции в частности, не движется и вдоль оси, потому что проекции этих внешних сил на ось уравновешивают друг друга.
Такого рода факт в механике формулируется уравнением общего равновесия стержня: суммарная проекция на ось Оz всех действующих на стержень внешних сил, равна нулю:
При построении уравнений общего равновесия механики принято использовать следующее правило знаков:
· Проекция усилия на ось положительна, если ее направление совпадает с выбранным направлением этой оси;
· И наоборот – проекция отрицательна, если направлена в противоположную сторону.
Эпюры – графики внутренних усилий, напряжений, перемещений, деформаций, возникающих в элементах конструкций и деталях машин под воздействием внешней нагрузки.
Напряжения при растяжении (сжатии) прямого стержня
Предположим, растягивающую брус внешнюю силу удалось распределить равномерно по его торцам.
Опыты показывают. Что в этом случае каждое продольное волокно бруса подвержено только растяжению и в любом его поперечном сечении внутренние силы действуют только по нормали к этим сечениям.
Поперечные сечения бруса, плоские до деформации, под действием внешних сил перемещаются параллельно своему начальному положению и остаются постоянными.
Растягивающие стержень внешние силы не всегда удается распределить по площади стержня равномерно.
Но опыты показывают, что поведение поперечных сечений растягиваемых стержней, расположенных на некотором расстоянии от места приложения внешней нагрузки, уже не зависит от способа приложения этих сил и всегда соответствует гипотезе плоских сечений.
При рассмотрении деформаций растяжения или сжатия, а также при рассмотрении последующих простых деформаций нами будет рассматриваться принцип Сен-Венана, названный по имени французского ученого XIX века, который заключается в том, что внутренние силовые факторы, возникающие в результате действия внешних сил, распределяются по сечениям рассматриваемого тела равномерно.
Рассмотрим стержень, подверженный действию продольных сил
Если на поверхность призматического стержня нанести сетку линий параллельных и перпендикулярных оси стержня, и приложить к нему растягивающую силу, то можно убедиться в том, что линии сетки и после деформации останутся взаимно-перпендикулярными, но расстояние между ними изменятся.
Все горизонтальные линии, например, cd, переместятся вниз, оставаясь горизонтальными и прямыми.
Можно предположить, что и внутри стержня будет происходить то же самое, т.е. поперечные сечения стержня плоские и нормальные к его оси до деформации, останутся плоскими и нормальными к оси и после деформации.
Эту гипотезу называют гипотезой плоских сечений (гипотезой Бернулли).
Продольная сила N есть равнодействующая нормальных напряжений в поперечном сечении:
поскольку , то
, отсюда
В частном случае, когда на стержень действует одна внешняя сила, из уравнения равновесия получим:
И вместо общей формулы получим частный вид формулы для растяжения:
Эти формулы справедливы и для сжатия, с той только разницей, что сжимающие напряжения считаются отрицательными.
Кроме того, сжатые стержни помимо расчета на прочность рассчитываются также и на устойчивость.
Очевидно, что эти напряжения в реальных условиях нельзя создавать больше или много меньше определенной величины. Поэтому вводится понятие допускаемого напряжения: — условие прочности.
Определение деформаций и перемещений. Закон Гука.
Опыты показывают, что при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются, при сжатии – наоборот.
Для многих материалов при нагружении до определенных пределов опыты показали следующую зависимость между относительным удлинением стержня и напряжением :
, где
— абсолютное удлинение стержня
— длина образца до деформации
— длина образца после деформации
Эта зависимость носит название закона Гука и формулируется следующим образом: линейные деформации прямо пропорциональны нормальным напряжениям.
— коэффициент, зависящий от материала, т.е. его способность сопротивляться деформированию. Он характеризует жесткость материала, т.е. его способность сопротивляться деформированию.
Для ст.3 .
Для других материалов значение можно найти в справочниках.
Имея ввиду, что для стержня постоянного сечения:
, а
Можно получить формулу для определения полного (абсолютного) удлинения (укорочения) стержня:
Между продольным удлинением и поперечным существует зависимость:
Здесь — коэффициент поперечной деформации (коэффициент Пуассона),который характеризует способность материала к поперечным деформациям.
При пользовании этой формулой удлинение считается положительным, а укорочение – отрицательным.
Для всех материалов .
Для стали при упругих деформациях можно принимать =0,3.
Зная можно определить полное поперечное сужение или расширение стержня : , где — поперечный размер стержня до деформации
— поперечный размер стержня после деформации.
В стержнях переменного сечения напряжения в поперечных сечениях можно считать распределенными равномерно (если угол конусности ) и определять их по той же формуле, что и для стержня постоянного сечения.
Для определения деформаций стержня переменного сечения, в поперечных сечениях которого действует продольная сила N, найдем сначала удлинение элемента длиной , которое является дифференциалом полного удлинения .
Согласно закону Гука, имеем:
Полное удлинение стержня получим, интегрируя выражение в пределах :
, если и — величины постоянные, то
Чтобы воспользоваться этой формулой, необходимо знать закон изменения в зависимости от .
Для ступенчатых стержней интегрирование заменяется суммирование, и полное изменение длины бруса определяется как алгебраическая сумма деформаций его отдельных частей, в пределах которых :
Например, для стержня изображенного на схеме, имеем:
Определим теперь удлинение стержня постоянного сечения под действием силы тяжести, которая представляет собой нагрузку, равномерно распределенную вдоль стержня.
Удельный вес материала обозначим через .
Рассмотрим деформацию элемента , выделенного на расстоянии от нижнего конца.
Удлинение элемента равно:
Интегрируя это выражение в пределах, получим
Это выражение можно представить в другом виде, если учесть, что сила тяжести бруса равна: или , тогда получим — формула по определению перемещения с учетом собственного веса при известной длине
Следовательно, удлинение бруса постоянного сечения от собственной силы тяжести в два раза меньше удлинения от действия силы, равной силе тяжести и приложенной к его концу.
Опытное изучение свойств материалов
Для изучения свойств материалов и установления значения предельных (по разрушению или по пластическим деформациям) производят испытания образцов материала вплоть до разрушения. По виду деформации различают испытания на растяжение, сжатие, кручение и изгиб.
Испытания производят при статической и ударной (испытание на усталость и выносливость) нагрузках на ГМС – 50.
Цель испытания на растяжение – определение механических характеристик материала.
При проведении испытания автоматически записывается диаграмма зависимости между растягивающей силой и удлинением образца.
Условия и порядок выполнения работы
1. Стальной стержень ступенчатого сечения находится под действием внешней силы и собственного веса.
2. Необходимо построить эпюры:
· нормальных продольных сил
· нормальных напряжений
· перемещения сечений стержня относительно жесткой заделки.
Площадь большего поперечного сечения стержня в 2 раза превышает меньшую.
Источник
