Презентация растяжение и сжатие вдоль осей координат

Слайд 1
Преобразования графиков. Параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой y = x, растяжение и сжатие вдоль осей координат.
Слайд 2
ЦЕЛИ: Повторить определение функции; основные понятия, связанные с ней; Повторить способы задания функции. Ввести понятие чётной и нечётной функции. Освоить основные способы преобразования графиков.
Слайд 3
ПЛАН 1.Повторение Определение функции. Способы задания функции 2.Преобразование графиков функции Симметрия относительно оси у, f(x) → f( — x) Симметрия относительно оси х, f(x) → — f(x) Параллельный перенос вдоль оси х, f(x) →f(x -а ) Параллельный перенос вдоль оси у, f(x) → f(x) + b Сжатие и растяжение вдоль оси х, f(x) → f( α x), α >0 Сжатие и растяжение вдоль оси у, f(x) → kf(x),k>0 Построение графика функции у = | f (x) | Построение графика функции у = f( | x | ) Построение графика обратной функции
Слайд 4
ОПРЕДЕЛЕНИЕ ФУНКЦИИ Числовой функцией называется соответствие, которое каждому числу х из некоторого заданного множества сопоставляет единственное число у. Обозначение: у = f (х), где х –независимая переменная (аргумент функции), у –зависимая переменная (функция). Множество значений х называется областью определения функции.( D ) Множество значений у называется областью значения функции.(Е) D E y x y = f (x)
Слайд 5
Пример№1 у = √х – 2 + 3 При х = 6, у(6) = √6 – 2 + 3 = 5 Найдём область определения. х — 2 ≥ 0, х ≥2 ⇒ D (у) = [ 2; +∞); Так как по определению арифметического корня 0 ≤ √х – 2 ≤ +∞, 0 + 3≤ √х – 2 + 3 ≤ +∞+ 3, или 3 ≤ у ≤ +∞, Е(х) = [ 3; +∞)
Слайд 6
Пример № 2. Найти область определения и область значения функции f (x) = 3 + 1 . х-2 Функция определена при х — 2 ≠ 0, то есть х ≠ 2 ⇒ D (у) = (-∞;2) U (2; +∞); Так как при всех допустимых значениях х дробь 1/(х-2) не обращается в нуль, то функция f (x) принимает все значения, кроме 3. Поэтому Е( f ) = (-∞;3) U (3; +∞);
Слайд 7
Пример №3 . Найти область определения дробно-рациональной функции f (x) = 1 + 3 х + 4 . х-2 (х — 1)(х + 3) Знаменатели дробей обращаются в нуль при х = 2, х = 1, х = -3. Поэтому область определения D ( f ) = (-∞; -3 ) U ( -3; 1 ) U ( 1 ; 2 ) U (2; +∞);
Слайд 8
Пример №4 . Зависимость 2 х – 3 х 2 + 1 Уже не является функцией. При х = 1, пользуясь верхней формулой, найдём у = 2*1 – 3 = -1, а пользуясь нижней формулой, получим у = 1 2 + 1 = 2. Таким образом, одному значению х =1 соответствуют два значения у (у=-1 и у=2). Поэтому эта зависимость (по определению) не является функцией у(х) =
Слайд 9
СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ Аналитический способ : функция задаётся с помощью формулы. Примеры: у = х 2 , у = ax + b Табличный способ : функция задаётся с помощью таблицы. Описательный способ : функция задаётся словесным описанием. Графический способ : функция задаётся с помощью графика.
Слайд 10
ОПРЕДЕЛЕНИЕ ГРАФИКА ФУНКЦИИ Графиком функции называется множество точек плоскости с координатами (х; f (х)) у х 1 f (х 1 ) х 2 f (х 2 ) х
Слайд 11
Пример №5 . Дана функция у = 2 х – 3 | х | + 4. Принадлежит ли графику этой функции точка с координатами а) (-2; -6); б) (-3; — 10) Решение. а) при х = -2, у = 2· (-2) -3· |-2| + 4 = — 4 — 3 · 3 + 4 =-6 Так как у(-2) = -6, то точка А(-2; -6) принадлежит графику функции. б) при х = -3, у = 2· (-3) -3· |- 3 | + 4 = — 6 — 3 · 3 + 4 =- 11 Так как у(-3) = -11, то точка В(-3; -10) не принадлежит графику функции
Слайд 12
Пример №6 . Дана функция f (х) = — х 2 + 6х – 8. Найдём точки пересечения графика функции с осями координат. Решение. 1) Точка пересечения с осью ординат, при х=0, у(0) = — 0 2 + 6·0 – 8 = — 8. Получаем координаты этой точки А(0; -8) 2) Точка пересечения с осью абсцисс, при у =0, 0 = — х 2 + 6х – 8, х 2 — 6х + 8=0 , D = 36 – 32 =4, x 1 = (6-2)/2=2, x 1 = (6+2)/2=4. Поэтому график функции пересекает ось абсцисс в двух точках: В(2; 0) и С(4;0)
Слайд 13
Симметрия относительно оси у f(x) → f( — x) Графиком ф-и у = f ( — х ) получается преобразованием симметрии графика ф-и у = f ( х ) относительно оси у. у = х 2 = (-х) 2 у=√х у = f ( -х ) у у у х х х у= f (х) у=√-х
Слайд 14
Симметрия относительно оси х f(x) → — f(x) График ф-и у = — f ( х ) получается преобразованием симметрии графика ф-и у = f ( х ) относительно оси х. у = х 2 у= — sinx у= f (х) у = — х2 у = — f ( х ) у= sinx у у у х х х
Слайд 15
Чётность и нечётность Функция наз-ся чётной, если: область определения функции симметрична относительно нуля, для любого х из области определения f (- х) = f (х) График чётной функции симметричен относительно оси у Функция наз-ся нечётной , если: область определения функции симметрична относительно нуля, для любого х из области определения f (- х) = — f (х) График нечётной функции симметричен относительно начала координат х у х у
Слайд 16
Параллельный перенос вдоль оси х, f(x) →f(x -а ) Графиком ф-и у = f ( х- a) получается парал – лельным переносом графика ф-и вдоль оси х на |a| вправо при а > 0 и влево при а
Слайд 17
Параллельный перенос вдоль оси у, f(x) → f(x) + b Графиком ф-и у = f ( х ) + b получается парал – лельным переносом графика ф-и у = f ( х ) вдоль оси y на |b| вверх при b > 0 и вниз при b
Слайд 18
Сжатие и растяжение вдоль оси х, f(x) → f( α x), α >0 График функции у = f ( α x) получается сжатием графика функции у = f (x) вдоль оси х в α раз при α > 1 График функции у = f ( α x) получается растяже- нием графика функции у = f (x) вдоль оси х в 1/ α раз при 0
Слайд 19
Сжатие и растяжение вдоль оси у, f(x) → kf(x),k>0 График функции у = kf (x) получается сжатием графика функции у = f (x) вдоль оси y в 1/k раз при 0 1 у=1/2х 2 у=2 sinx у=1/2 sinx у у у= sinx х х х у= kf(x) у= kf(x) у= f(x) у
Слайд 20
Построение графика функции у= | f(x)| Части графика функции у = (х), лежащие выше оси х и на оси х остаются без изменения, лежащие ниже оси х – симметрично отражаются относительно этой оси (вверх) 1 3 0 1 у у у х х х y=|log 2 x| y=|x 2 -4x+3| y=|sinx| y=log 2 x y=sinx y=x 2 -4x+3
Слайд 21
Построение графика функции у= f(|x|) Часть графика функции у = (х), лежащая левее оси х и на оси у удаляется, а часть, лежащая правее оси у — остаётся без изменения и, кроме того, симметрично отражается относительно оси у (влево). Точка графика, лежащая на оси у, остаётся неизменной. у у y=x 2 -4|x|+3 х х y=x 2 -4x+3 y=sinx y=sin|x|
Слайд 22
Построение графика обратной функции График ф-и у = g( х ), обратной данной для функции у = f ( х ) , можно получить преобразованием симметрии графика ф-и у = f ( х ) относительно прямой у= х. 1 1 0 1 0 1 y=cosx -1 0 1 y=sinx у у у х х х у = 2 х y= log2x y=arcsinx y =arccosx
Слайд 23
Практическая часть: Построить графики функций: 1) y= sin(x- ); 2) y= sin(x- /4); 3) y= 2sin(x)-1; 4) y= -cos(x) 5) y= cos(x- /2); 6) y= cos(x)-1; 7) y= 2cos(x+ /4)+1; 8) y = 2 arccos x
Слайд 24
Контрольные вопросы Дайте определение чётной, нечётной функций. Расскажите о способах задания функции. Что такое область определения? Что такое область значения? Как найти точки пересечения с осями координат? Какие свойства симметрии вы рассмотрели? Как проявляются свойства симметрии на графиках?
Источник
Презентация на тему: » Растяжение и сжатие графиков функцийРастяжение и сжатие графиков функций.» — Транскрипт:
1
Растяжение и сжатие графиков функций
2
График функции при k>1 можно получить из графика функции растяжением от оси х исходного графика в k раз, а при 0
3
4
5
Построить график функции f(x)=0,5x.
6
В этой же системе координат построить график функции y=1,5f(x). График данной функции можно получить из графика функции y=f(x) путем растяжения от оси абсцисс в 1,5 раза.
7
График функции можно получить из графика функции с помощью симметрии относительно оси х
8
В этой же системе координат построить график функции y=-1,5f(x)
9
Постройте график функции
10
11
12
Постройте график функции 1.
13
2.
14
Постройте график функции 1.
15
2.
16
Постройте график функции 740 G(x)=
17
740
Источник

МБОУ « СОШ № 77» г. Новокузнецка, Кемеровской области
Федоров a Т. А., учитель математики
 0 График функции у = f (x-a) получается из графика функции у = f (x) смещением графика на а единиц вправо вдоль оси ох. 0 х а » width=»640″
0 График функции у = f (x-a) получается из графика функции у = f (x) смещением графика на а единиц вправо вдоль оси ох. 0 х а » width=»640″
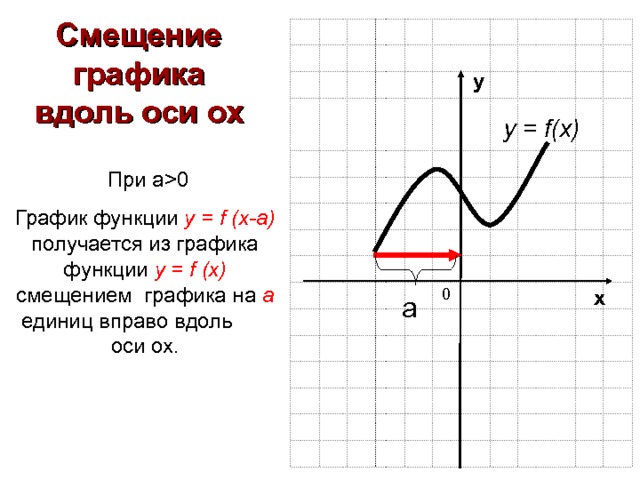
Смещение графика вдоль оси ох
у
у = f(x)
При а 0
График функции у = f (x-a) получается из графика функции у = f (x) смещением графика на а единиц вправо вдоль оси ох.
х
а
у = х 2
у = ( х-3) 2
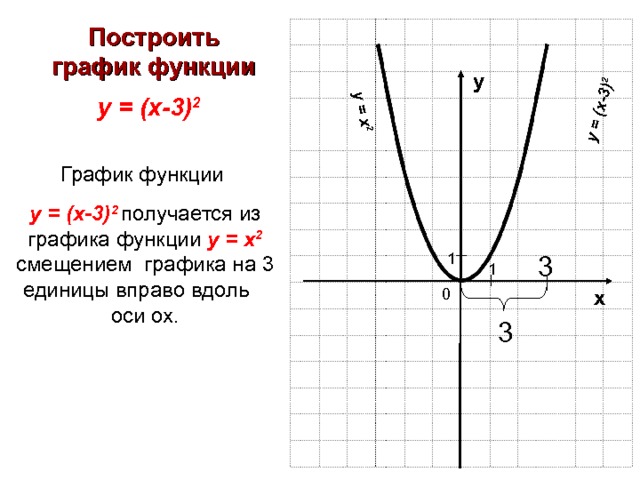
Построить график функции у = ( х-3) 2
у
График функции
у = ( х-3) 2 получается из графика функции у = х 2 смещением графика на 3 единицы вправо вдоль оси ох.
1
3
1
х
3
 0 График функции у = f (x + a) получается из графика функции у = f (x) смещением графика на а единиц влево вдоль оси ох. 0 х а » width=»640″
0 График функции у = f (x + a) получается из графика функции у = f (x) смещением графика на а единиц влево вдоль оси ох. 0 х а » width=»640″
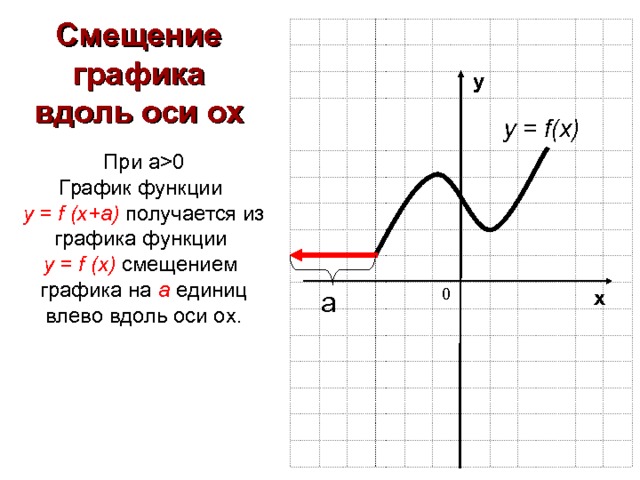
Смещение графика вдоль оси ох
у
у = f(x)
При а 0
График функции
у = f (x + a) получается из графика функции
у = f (x) смещением графика на а единиц влево вдоль оси ох.
х
а
у = ( х+3) 2
у = х 2
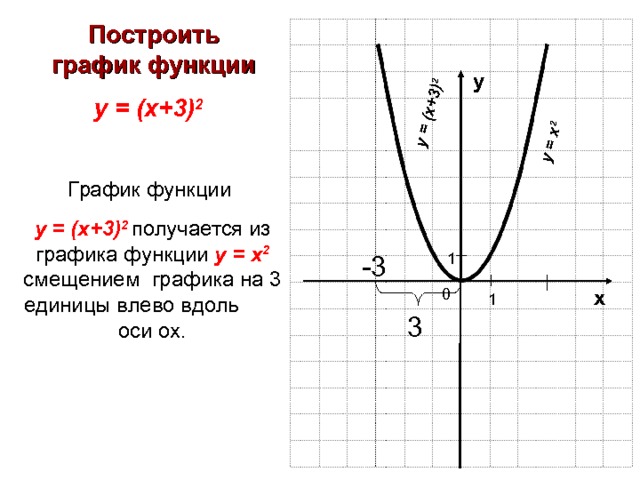
Построить график функции у = ( х+3) 2
у
График функции
у = ( х+3) 2 получается из графика функции у = х 2 смещением графика на 3 единицы влево вдоль оси ох.
-3
1
х
1
3
 0 График функции у = f (x ) -a получается из графика функции у = f (x) смещением графика на а единиц вниз вдоль оси оу. 0 х а » width=»640″
0 График функции у = f (x ) -a получается из графика функции у = f (x) смещением графика на а единиц вниз вдоль оси оу. 0 х а » width=»640″
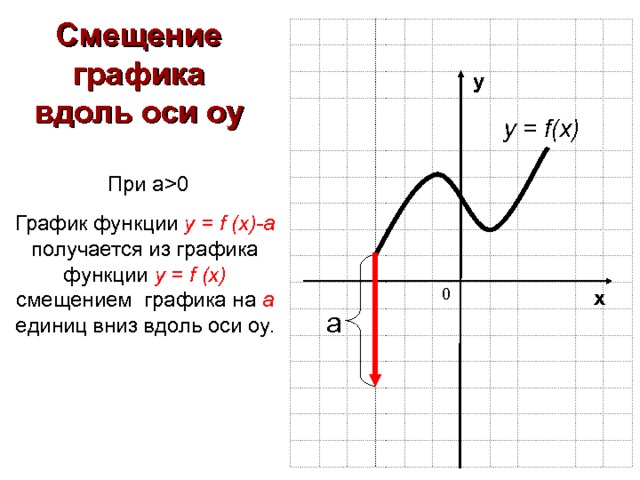
Смещение графика вдоль оси оу
у
у = f(x)
При а 0
График функции у = f (x ) -a получается из графика функции у = f (x) смещением графика на а единиц вниз вдоль оси оу.
х
а
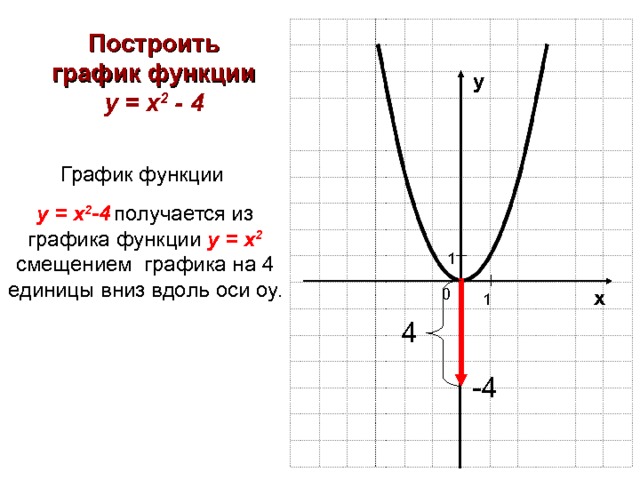
Построить график функции у = х 2 — 4
у
График функции
у = х 2 -4 получается из графика функции у = х 2 смещением графика на 4 единицы вниз вдоль оси оу.
1
х
1
4
-4
 0 График функции f (x )+ a получается из графика функции f (x) смещением графика на а единиц вверх вдоль оси оу. а 0 х » width=»640″
0 График функции f (x )+ a получается из графика функции f (x) смещением графика на а единиц вверх вдоль оси оу. а 0 х » width=»640″
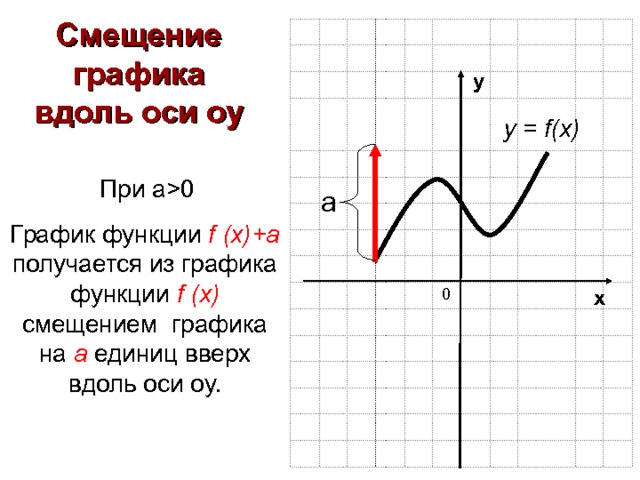
Смещение графика вдоль оси оу
у
у = f(x)
При а 0
График функции f (x )+ a получается из графика функции f (x) смещением графика на а единиц вверх вдоль оси оу.
а
х

Построить график функции у = х 2 + 4
у
График функции
у = х 2 +4 получается из графика функции у = х 2 смещением графика на 4 единицы вверх вдоль оси оу.
4
4
1
х
1
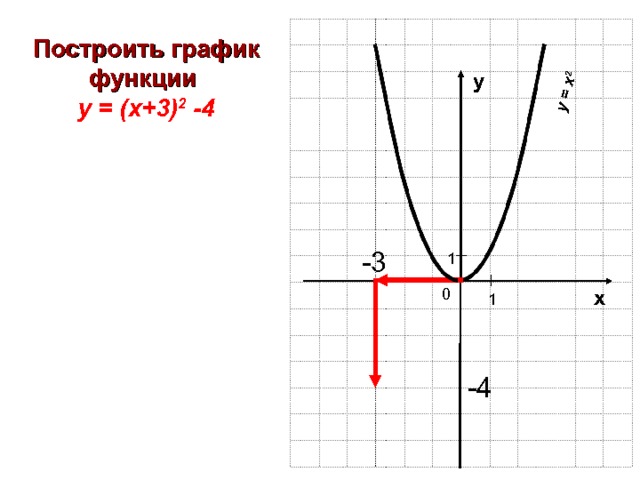
у = х 2
Построить график функции
у = ( х+3) 2 -4
у
-3
1
х
1
-4
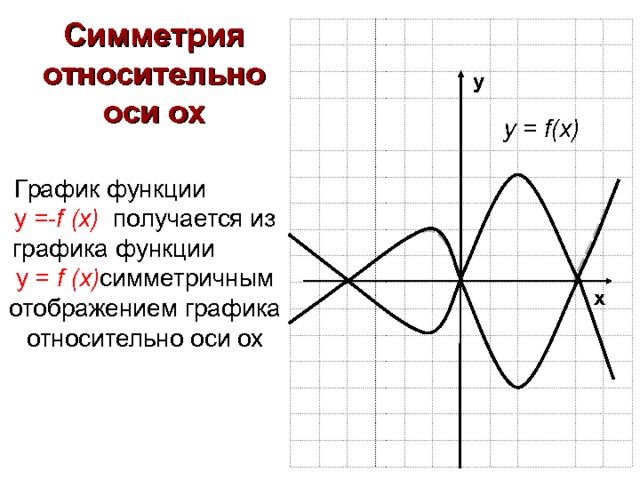
Симметрия относительно оси ох
у
у = f(x)
График функции у = — f (x ) получается из графика функции у = f (x) симметричным отображением графика относительно оси ох
х
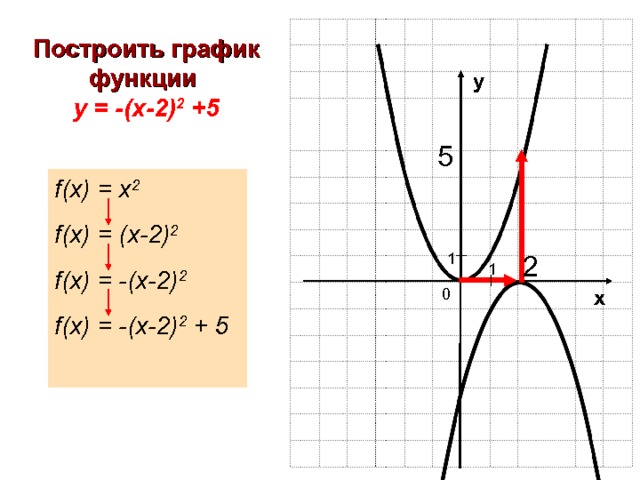
Построить график функции
у = — ( х-2) 2 +5
у
5
f(x) = x 2
f(x) = (x-2) 2
f(x) = -(x-2) 2
f(x) = -(x-2) 2 + 5
2
1
1
х
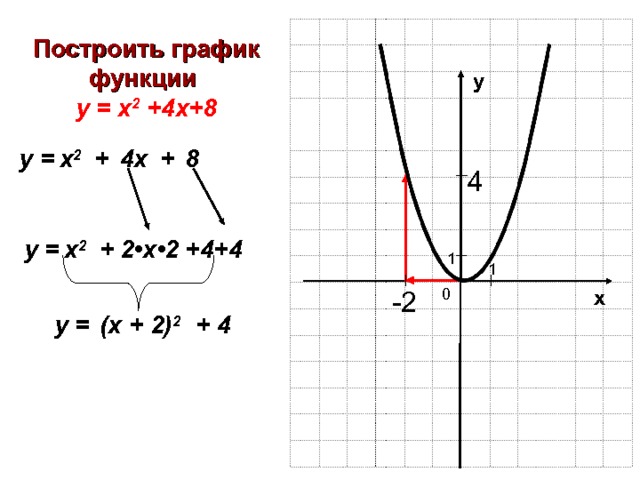
Построить график функции
у = х 2 +4х+8
у
х 2
+
у =
4х
+
8
4
2 • х •2
+4+4
х 2
+
у =
1
1
-2
х
(х + 2) 2
у =
+ 4
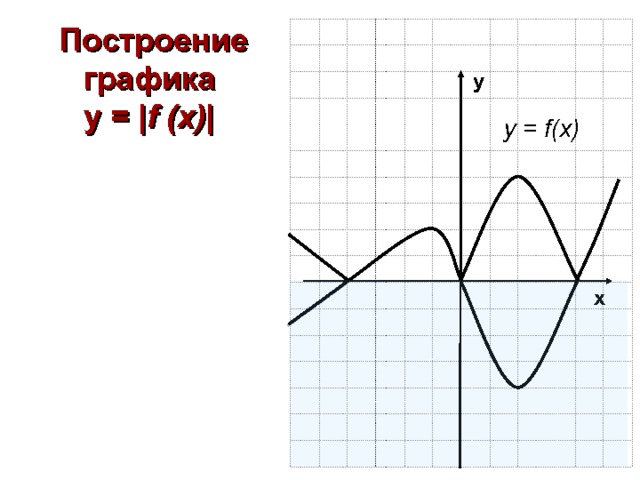
Построение графика y = | f (x) |
у
у = f(x)
х
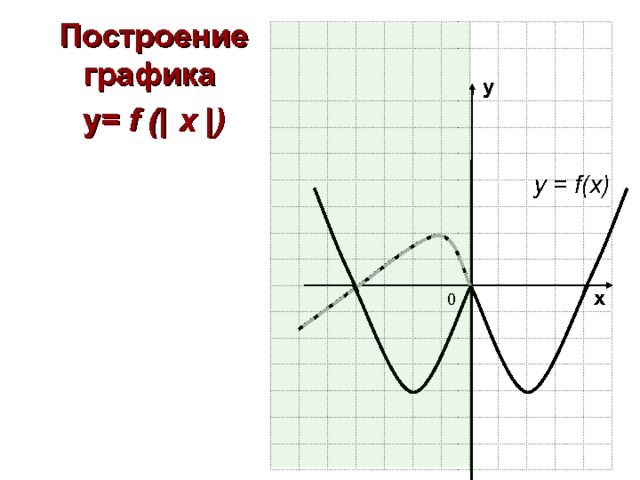
Построение графика y= f (| x |)
у
у = f(x)
х
 1 График функции у = k f (x ) получается из графика функции у = f (x) растяжением вдоль оси оу, если k1 у = f(x) х 0 » width=»640″
1 График функции у = k f (x ) получается из графика функции у = f (x) растяжением вдоль оси оу, если k1 у = f(x) х 0 » width=»640″
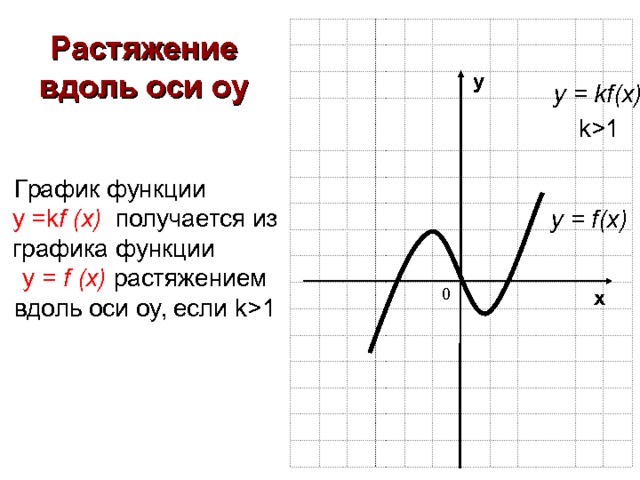
Растяжение вдоль оси оу
у
у = kf(x)
k 1
График функции у = k f (x ) получается из графика функции у = f (x) растяжением вдоль оси оу, если k1
у = f(x)
х
Растяжение вдоль оси оу
y
1
I I I I I I I
O
x
— 1
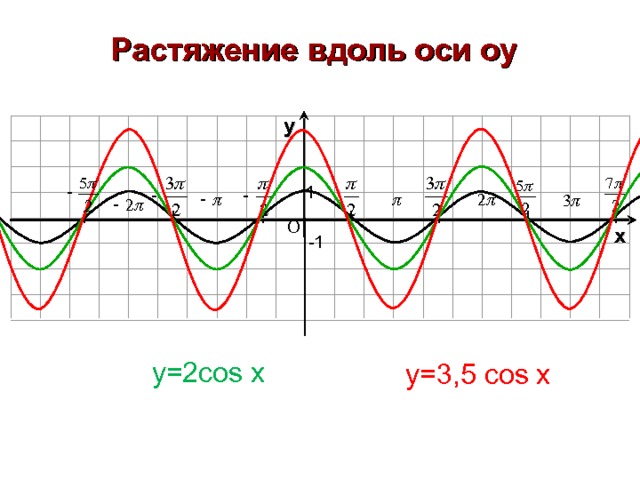
y=2cos x
y =3,5 cos x
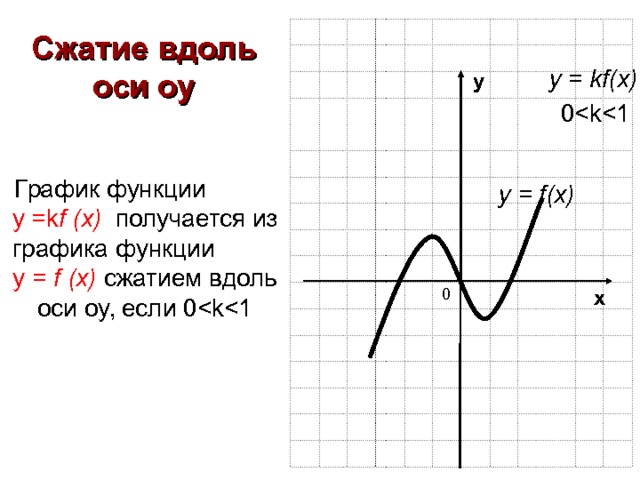
Сжатие вдоль оси оу
у = kf(x)
у
График функции у = k f (x ) получается из графика функции у = f (x) сжатием вдоль оси оу, если 0
у = f(x)
х
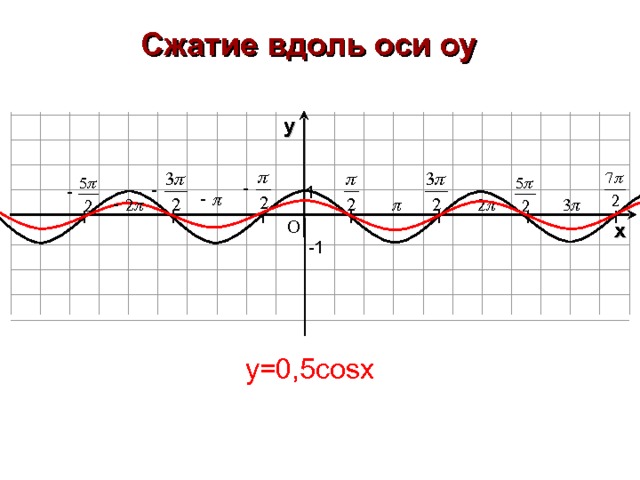
Сжатие вдоль оси оу
y
1
I I I I I I I
O
x
— 1
y=0,5cosx
 1 х 0 » width=»640″
1 х 0 » width=»640″
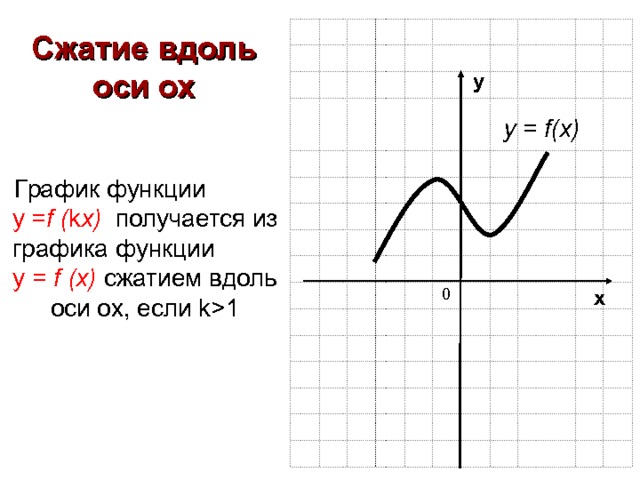
Сжатие вдоль оси ох
у
у = f(x)
График функции у = f ( k x ) получается из графика функции у = f (x) сжатием вдоль оси ох, если k1
х
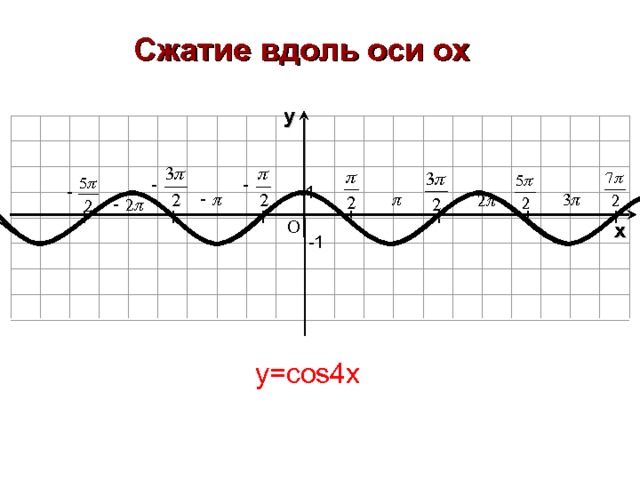
Сжатие вдоль оси ох
y
1
I I I I I I I
O
x
— 1
y =cos4x
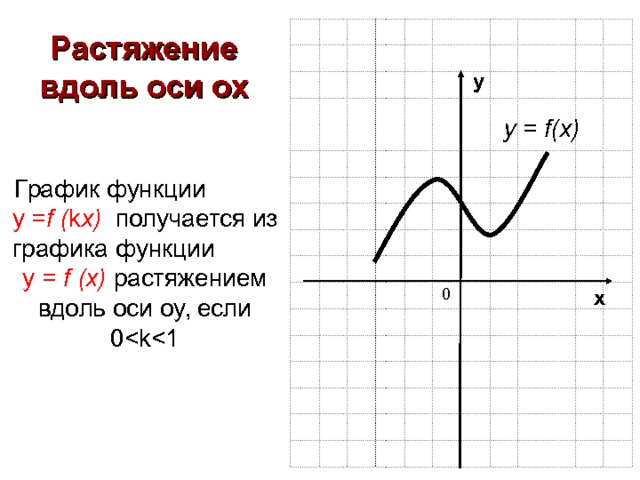
Растяжение вдоль оси ох
у
у = f(x)
График функции у = f ( k x ) получается из графика функции у = f (x) растяжением вдоль оси оу, если 0
х
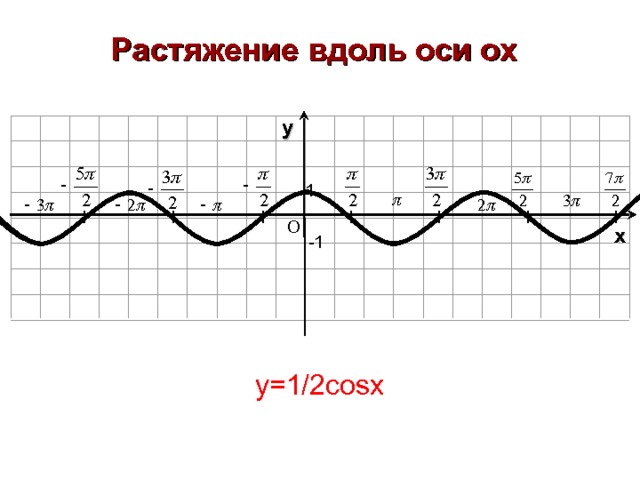
Растяжение вдоль оси ох
y
1
I I I I I I I
O
x
— 1
y=1/2cosx
 2 у -1 2 1 1 0 х » width=»640″
2 у -1 2 1 1 0 х » width=»640″
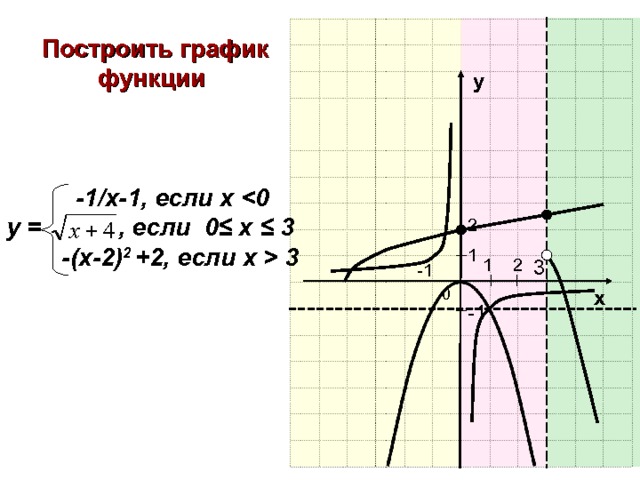
Построить график функции
1/x , если х -1
у = -х 2 ,если -1 ≤ x ≤ 2
2х-8,если х 2
у
-1
2
1
1
х
 3 у 2 1 3 1 2 -1 0 х -1 » width=»640″
3 у 2 1 3 1 2 -1 0 х -1 » width=»640″
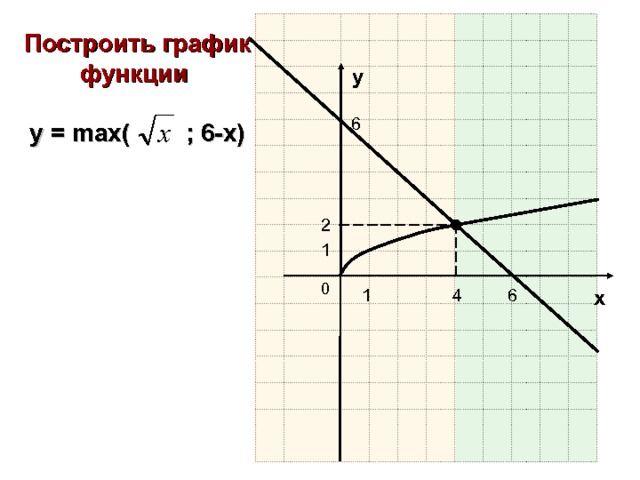
Построить график функции
— 1/x -1, если х
у = , если 0≤ x ≤ 3
-(х-2) 2 +2, если х 3
у
2
1
3
1
2
-1
х
-1
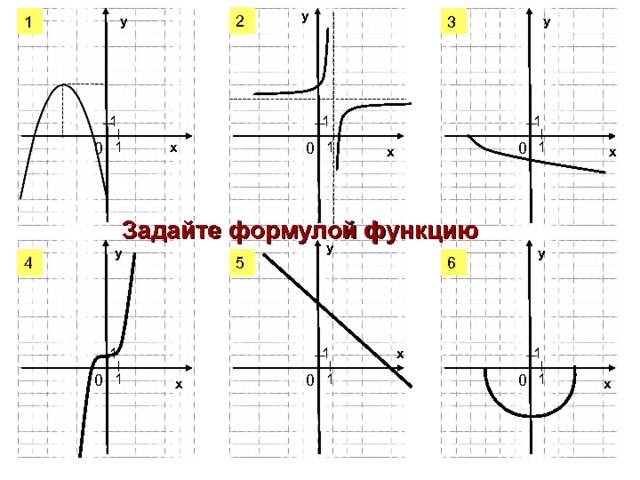
Построить график функции
у = max( ; 6-х)
у
6
2
1
6
4
х
1
у
2
1
3
у
у
1
1
1
1
х
1
1
х
х
Задайте формулой функцию
у
у
у
5
6
4
х
1
1
1
1
1
1
х
х
Источник
Вы можете ознакомиться и скачать
Сжатие(растяжение) графика вдоль оси ординат — презентация по Геометрии_.
Презентация содержит 18 слайдов.
Презентации для любого
класса можно скачать бесплатно. Если материал и наш сайт презентаций Вам
понравились
–
поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в
своем
браузере.
Слайды и текст этой презентации
Слайд 1
Слайд 2
Описание слайда:
Определение.
Определение.
Алгоритм построения.
Зеркальное отражение графиков.
Примеры.
Задания.
Слайд 3
Описание слайда:
Рассмотрим функцию вида
Рассмотрим функцию вида
y = A∙f (x), где A>0. Можно заметить, что при равных значениях аргумента ординаты графика этой функции будут в А раз больше ординат графика функции y = f (x) при A>1, или в 1/A раз меньше ординат графика функции y = f (x) при A<1.
Слайд 4
Описание слайда:
Построить график функции y = f (x)
Построить график функции y = f (x)
Увеличить или уменьшить его ординаты в А раз.
Слайд 5
Описание слайда:
Рассмотрим функцию
Рассмотрим функцию
y = -f (x). При всех значениях аргумента ординаты графика функции y = -f (x) равны по абсолютной величине, но противоположны по знаку ординатам функции y = f (x).
Слайд 6
Описание слайда:
Для построения графика функции
Для построения графика функции
y = -f (x) следует построить график функции y = f (x)…
Слайд 7
Описание слайда:
… и отразить его симметрично относительно оси абсцисс.
… и отразить его симметрично относительно оси абсцисс.
Слайд 8
Описание слайда:
Соединяя знания о построении функции y = A∙f (x),
Соединяя знания о построении функции y = A∙f (x),
где A>1 с последним правилом, мы можем построить график функции y = A∙f (x) для значения А любого знака.
Слайд 9
Слайд 10
Слайд 11
Описание слайда:
Строим график функции y=x3
Строим график функции y=x3
Слайд 12
Описание слайда:
Строим график функции y=x3
Сжимаем его вдоль оси ординат в 2 раза
Слайд 13
Описание слайда:
Строим график функции y=x3
Строим график функции y=x3
Сжимаем его вдоль оси ординат в 2 раза
Отображаем симметрично относительно оси абсцисс.
Слайд 14
Описание слайда:
Построить график функции
Построить график функции
y= -2sin x.
Слайд 15
Описание слайда:
Строим график функции y=sin x
Строим график функции y=sin x
Слайд 16
Описание слайда:
Строим график функции y=sin x
Строим график функции y=sin x
Растягиваем его вдоль оси ординат в 2 раза
Слайд 17
Описание слайда:
Строим график функции y=sin x
Строим график функции y=sin x
Растягиваем его вдоль оси ординат в 2 раза
Отражаем симметрично относительно оси абсцисс.
Слайд 18
Источник
