Преобразования графиков функций растяжение и сжатие вдоль оси ординат
Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее не постоянно хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.

1. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.

Теперь растяжение графика. Или сжатие.
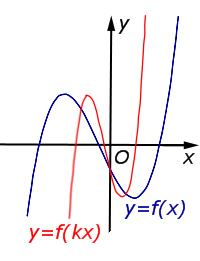
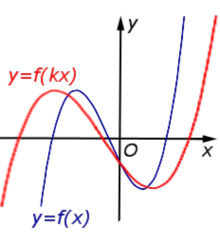
2. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если

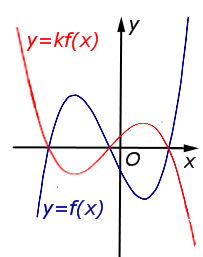
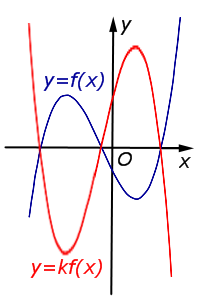
3. Растяжение (сжатие) по вертикали
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если

И отражение по горизонтали.
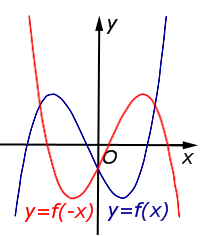
4. Отражение по горизонтали
График функции симметричен графику функции относительно оси Y.


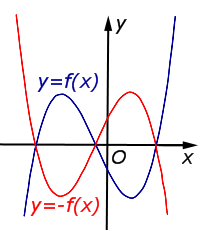
5. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.

Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
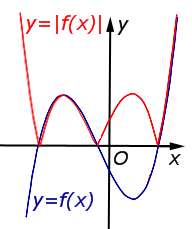
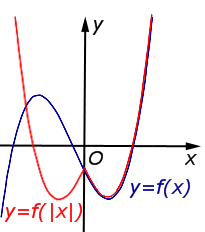
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
6. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.

Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.

Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.

Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1. Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке

2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка

Продолжение — в статье «Построение графиков функций».
Источник
Преобразования
графиков функций – это линейные преобразования функции y
= f(x) или её аргумента х к виду
y
= af(kx
+ b) + m,
а так же
преобразование с использованием модуля.
Зная,
как строить графики функции y =
f(x), где
y
= kx + b,
y
= ax2,
y
= xn,
y
= k/x,
y
= ax,
y
= logax,
можно
построить график функции
y
= af(kx
+ b) + m.
ОБЩИЙ ВИД ПРЕОБРАЗОВАНИЯ ФУНКЦИИ
Параллельный
перенос графика вдоль оси абсцисс на |b| единиц.
y
= f(x–
b)
вправо,
если b ˃ 0;
влево,
если b < 0.
y
= f(x+
b)
влево,
если b ˃ 0;
вправо,
если b < 0.
ПРИМЕР:
Построить график функции
у =
(х + 2)3.
Построим график функции у =
х3 и
параллельно перенесём его влево на 2 единицы вдоль оси х (так как 2 ˃ 0). Получим график
функции
у = (х + 2)3.
ПРИМЕР:
Построить график функции
у =
(х – 3)2.
Построим график функции у =
х2 и
параллельно перенесём его вправо на 3 единицы вдоль оси х (так как –3 < 0). Получим график
функции
у =
(х – 3)2.
Параллельный
перенос графика вдоль оси ординат на |m| единиц.
y
= f(x) + m
вверх,
если m ˃ 0;
вниз,
если m < 0.
ПРИМЕР:
Построить график функции
у =
х2 – 5.
Построим график функции у =
х2 и
параллельно перенесём его вниз на 5 единиц вдоль оси у (так как –5 < 0). получим график
функции
у =
х2 – 5.
ПРИМЕР:
Построить график функции
у =
√͞͞͞͞͞х + 4.
Построим график функции у =
√͞͞͞͞͞х и параллельно перенесём его вверх на 4 единицы
вдоль оси у (так как
4 ˃ 0). Получим график функции
у =
√͞͞͞͞͞х + 4.
Отражение
графика.
y
= f(–x)
Симметричное
отражение графика относительно оси ординат.
ПРИМЕР:
Построить график функции
у =
–х + 3.
Построим график функции у =
х + 3 и отобразим
полученный график симметрично относительно оси
у и получим график
функции
у =
–х + 3
y
= –f(x)
Симметричное
отражение графика относительно оси абсцисс.
ПРИМЕР:
Построить график функции
у =
–(х – 3)2.
Построим график функции у =
х2 и
параллельно перенесём его вправо на 3 единицы вдоль оси х (так как –3 < 0). получим график
функции
у =
(х – 3)2.
отобразим полученный график симметрично относительно
оси х и получим
график функции
у =
–(х – 3)2.
Сжатие
и растяжение графика.
y
= f(kx)
При k ˃ 1 –
сжатие графика к оси ординат в k раз,
при 0 < k<
1 – растяжение графика от оси ординат в k раз,
ПРИМЕР:
Построить график функции
у =
(3х)2.
Построим график функции у =
х2. Выполним
сжатие графика функции в три раза до оси у и получим
график функции
у =
(3х)2.
ПРИМЕР:
Построить график функции
Построим график функции у =
√͞͞͞͞͞х. Выполним
растяжение графика функции в 1/3 от оси
у и получим график
функции
y
= kf(x)
При k ˃ 1 –
растяжение графика от оси абсцисс в k раз,
при 0 < k<
1 – сжатие графика к оси абсцисс в k раз.
ПРИМЕР:
Построить график функции
у =
3√͞͞͞͞͞х.
Построим график функции у =
√͞͞͞͞͞х .
Выполним
растяжение графика функции в три раза относительно оси х и получим
график функции
у =
3√͞͞͞͞͞х.
ПРИМЕР:
Построить график функции
у =
1/3 х3.
Построим график функции у =
х3. Выполним
сжатие графика функции у = х3 в три раза к оси х и получим
график функции
у =
1/3 х3.
Преобразования
графика с модулем.
у = |f(x)|
При f(x)
˃ 0 – график остаётся без изменений,
при f(x) <
0 – график симметрично отражается
относительно оси абсцисс.
ПРИМЕР:
Построить график функции
у =
|х2 – 6|
Построим график функции у = х2. Параллельно переносимо график вниз на 6 единиц
вдоль оси у и получим график функции
у =
х2 – 6.
Отобразим симметрично относительно оси х ту
часть графика, которая находится под осью, и получим график функции
у =
|х2 – 6|
ПРИМЕР:
Построить график функции
у =
|х3|
Отобразим симметрично относительно оси х ту
часть графика, которая находится под осью, и получим график функции
у =
|х3|
у =f(|x|)
При x ≥ 0 – график остаётся без изменений,
при x < 0 – график симметрично отражается относительно оси ординат.
ПРИМЕР:
Построить график функции
у =
(|x| – 1)2.
Построим график функции у =
х2 и
параллельно перенесём его вправо на 1 единицы вдоль оси х и получим график
функции
у =
(х – 1)2.
Оставляем ту часть графика, которая соответствует
неотрицательным значением х. Симметрично
отображаем относительно оси у часть полученного графика для неотрицательных
х и получаем график
функции
у
= (|x|
– 1)2.
ПРИМЕР:
Построить график функции
у =
5|x| – 3.
Построим график функции у =
5х и
параллельно перенесём его вниз на 3 единицы вдоль оси у и
получим график функции
у =
5x – 3.
Оставим ту часть графика, которая соответствует
неотрицательным значениям х.
Симметрично отобразим относительно оси у часть полученного графика для неотрицательных х и получим
график функции
у =
5|x| – 3.
Источник
Автор/ы проекта (ФИО)
Холева Ольга Вячеславовна
Должность (с указанием преподаваемого предмета)
учитель математики
Образовательное учреждение
МОУ СОШ №73 им.А.Ф.Чернонога г.Воронеж
Название проекта
«Преобразования графиков функций»
Операционная система, с помощью которой подготовлен мультимедийный компонент (Windows, Linux)
Windows
Форма (презентация, тест и т.п.)
презентация
Размер ресурса (мегабайт)
0,95Мб
Технические данные
(компьютер, интерактивная доска и другие.)
Компьютер, проектор, экран
Учебный предмет
Алгебра
Класс
9-10-11
Название учебного пособия и образовательной программы с указанием авторов, к которому относится ресурс
Программа основного общего образования
Учебники:
А.Н.Колмогоров и др. «Алгебра и начала анализа 10-11»
А.Г.Мордкович «Алгебра 8»
А.Г.Мордкович «Алгебра 9»
А.Г.Мордкович «Алгебра и начала анализа 10-11»
Ю.Н.Макарычев и др. «Алгебра 9»
Ю.Н.Макарычев и др. «Алгебра 9 с углубленным изучением математики»
Название темы или раздела учебного курса
Функции и их графики
Формат ресурса — основного файла (ppt, avi, exe, doc или другие)
ppt
Вид ресурса
(презентация, видео, текстовый документ, электронная таблица и другие)
презентация
Образовательный тип
(Поясняющий текст, учебный текст, методичка, разработанная программа, электронный тест, электронный учебник и другие)
учебный текст в виде презентации c графической информацией с анимационными эффектами
Средства Microsoft Office или другое ПО, с помощью которых создан дидактический материал
Microsoft Office PowerPoint
Цели, задачи дидактического материала
формировать знания и умения по построению графиков функций;
развивать навыки самостоятельной деятельности учащихся;
формирование и развитие познавательного интереса учащихся.
Содержание дидактического материала (раскрыть подробно)
Презентация содержит справочный материал по теме «Преобразования графиков функций». Состоит из нескольких разделов: правила преобразований, графические иллюстрации правил преобразований, примеры построения графиков функций с помощью преобразований.
Ресурсы дидактического материала (видео-фото, графические изображения, звуковые файлы, ссылки, анимационные и другие эффекты и т.п.)
Анимационные эффекты
Используемые источники информации (литература, Интернет, ЦОР и др.)
Учебники: А.Н.Колмогоров и др. «Алгебра и начала анализа 10-11», А.Г.Мордкович «Алгебра 8», А.Г.Мордкович «Алгебра 9», А.Г.Мордкович «Алгебра и начала анализа 10-11», Ю.Н.Макарычев и др. «Алгебра 9», Ю.Н.Макарычев и др. «Алгебра 9 с углубленным изучением математики».
Единая коллекция ЦОР https://School-collection.edu.ru
Возможности использования дидактического материала:
— педагогом на уроке (указать этапы урока);
— учащимися
Для использования учителем при объяснении нового материала и при повторении ранее изученного.
Данный материал обобщает традиционный учебник. Дидактический материал также предназначен для работы дома, для самостоятельного изучения или повторения данной темы.
Ограничения на использование ресурса (да, нет), описание ограничений
нет
Подробное объяснение места медиа-, мультимедиа компонента в структуре и содержании урока и пояснения по методике их использования в образовательном процессе.
Презентация будет полезна как при объяснении нового материала, так и при повторении темы «Построение графиков функций» в 9-10 -11 классах.
Использование дидактического материала позволяет сократить время на изучение или повторение, позволяет поддерживать устойчивое внимание, повышает интерес к предмету. Учитель может строить объяснение урока с использованием анимации в презентации с целью большего понимания излагаемой темы и наглядности.
Источник
Элементарные преобразования графика функции y = f (x ) перечислены в следующей таблице.
| Преобразование | Описание | Рисунок |
y = f (x + c), | В случае c > 0 график функции | 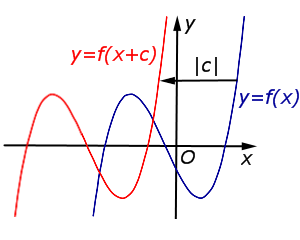 |
В случае c < 0 график функции | 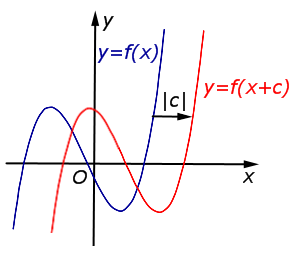 | |
y = f (x) + c, | В случае c > 0 график функции | 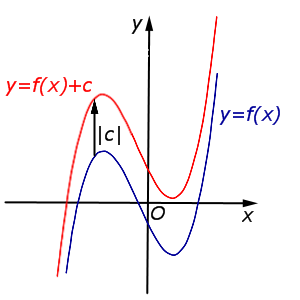 |
В случае c < 0 график функции | 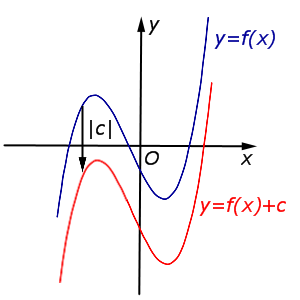 | |
| y = – f (x) | График функции y = f (x) симметрично отражается относительно оси Ox. | 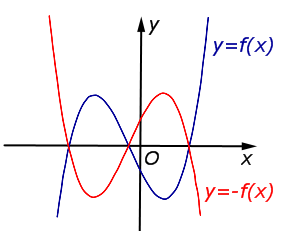 |
| y = f ( – x) | График функции y = f (x) симметрично отражается относительно оси Oy. | 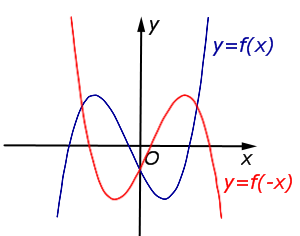 |
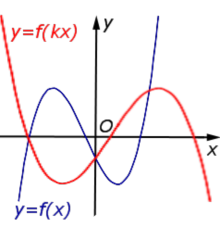
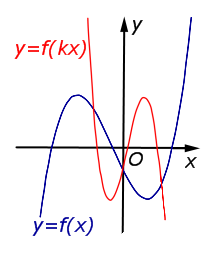
y = f (kx), | В случае k > 1 происходит | 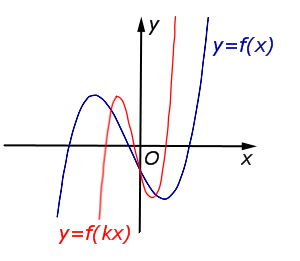 |
В случае 0 < k < 1 происходит растяжение графика функции | 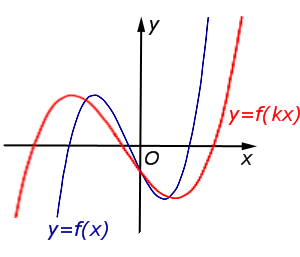 | |
В случае – 1 < k < 0 происходит растяжение графика функции | 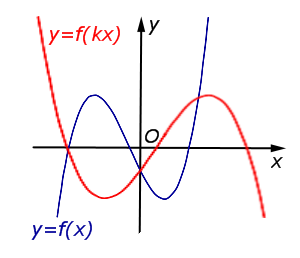 | |
В случае k < – 1 происходит | 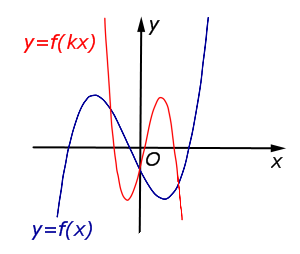 | |
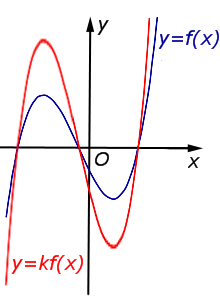
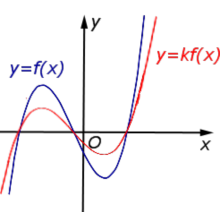
y = k f (x), | В случае k > 1 происходит | 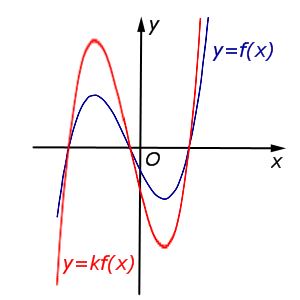 |
В случае 0 < k < 1 происходит | 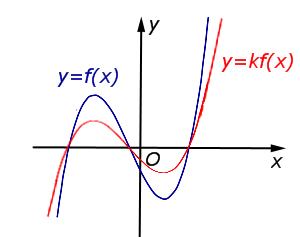 | |
В случае – 1 < k < 0 происходит | 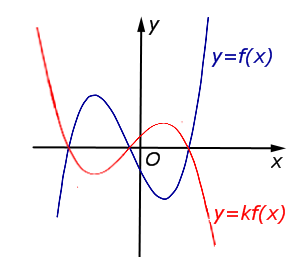 | |
В случае k < – 1 происходит | 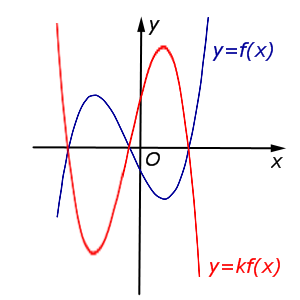 | |
| y = | f (x)| | Часть графика функции y = f (x), расположенная в области | 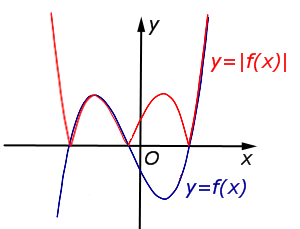 |
| y = f (| x|) | Ось Oy является осью симметрии Часть графика функции y = f (x), расположенная в области остаётся на месте. при помощи симметричного отражения относительно оси Oy. | 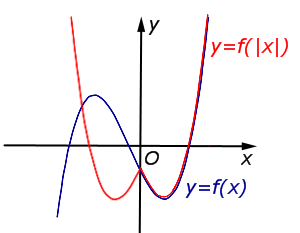 |
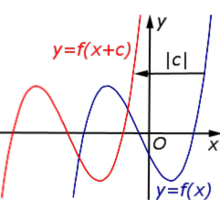
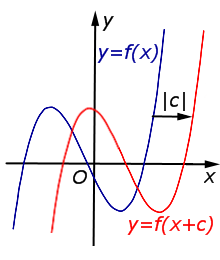
| Преобразование y = f (x + c), где c – число | |
В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | |  |
В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | |  |
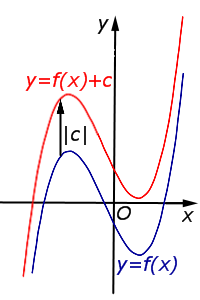
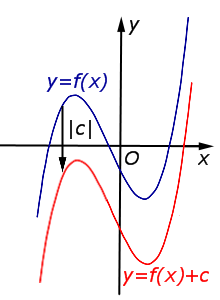
| Преобразование y = f (x) + c, где c – число | |
В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | |  |
В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | |  |
| Преобразование y = – f (x) | |
График функции y = f (x) симметрично отражается относительно оси Ox. |  |
| Преобразование y = f ( – x) | |
График функции y = f (x) симметрично отражается относительно оси Oy. |  |
| Преобразование y = f (kx), где k – число | |
В случае k > 1 происходит сжатие графика функции |  |
В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. |  |
В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. |  |
В случае k < – 1 происходит сжатие графика функции |  |
| Преобразование y = k f (x), где k – число | |
В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. |  |
В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. |  |
В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. |  |
В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. |  |
| Преобразование y = | f (x)| | |
Часть графика функции | 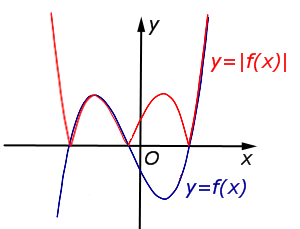 |
| Преобразование y = f (| x|) | |
Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции |  |
| Преобразование y = f (x + c), где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок:
|
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок:
|
| Преобразование y = f (x) + c, где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок:
|
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок:
|
| Преобразование y = – f (x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок:
|
| Преобразование y = f ( – x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок:
|
| Преобразование y = f (kx), где k – число |
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок:
|
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. Рисунок:
|
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок:
|
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок:
|
| Преобразование y = k f (x), где k – число |
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок:
|
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. Рисунок:
|
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок:
|
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок:
|
| Преобразование y = | f (x)| |
Описание: Часть графика функции y = f (x), расположенная в области , остаётся на месте. Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox. Рисунок:
|
| Преобразование y = f (| x|) |
Описание: Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции y = f (x), расположенная в области остаётся на месте. Часть графика функции y = f (| x|), расположенная в области x < 0, получается из части графика, расположенной в области при помощи симметричного отражения относительно оси Oy. Рисунок:
|
Примеры элементарных преобразований графика функции y = x2 приведены в следующей таблице.
| Функция | График |
| y = x2 = f (x) | 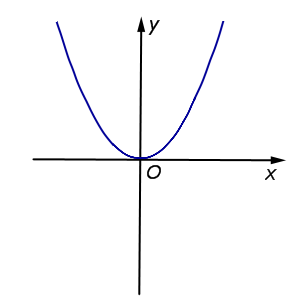 |