Потеря устойчивости при растяжении
Продольный изгиб
При расчетах на прочность подразумевалось, что равновесие конструкции под действием внешних сил является устойчивым. Однако выход конструкции из строя может произойти из-за того, что равновесие конструкций в силу тех или иных причин окажется неустойчивым. Во многих случаях, кроме проверки прочности, необходимо производить еще проверку устойчивости элементов конструкций.
Состояние равновесия считается устойчивым, если при любом возможном отклонении системы от положения равновесия возникают силы, стремящиеся вернуть её в первоначальное положение.
Рассмотрим известные виды равновесия.

Неустойчивое равновесное состояние будет в том случае, когда хотя бы при одном из возможных отклонений системы от положения равновесия возникнут силы, стремящиеся удалить её от начального положения.
Состояние равновесия будет безразличным, если при разных отклонениях системы от положения равновесия возникают силы, стремящиеся вернуть её в начальное положение, но хотя бы при одном из возможных отклонений система продолжает оставаться в равновесии при отсутствии сил, стремящихся вернуть её в начальное положение или удалить от этого положения.
При потере устойчивости характер работы конструкции меняется, так как этот вид деформации переходит в другой, более опасный, способный привести её к разрушению при нагрузке значительно меньшей, чем это следовало из расчета на прочность. Очень существенно, что потеря устойчивости сопровождается нарастанием больших деформаций, поэтому явление это носит характер катастрофичности.
При переходе от устойчивого равновесного состояния к неустойчивому конструкция проходит через состояние безразличного равновесия. Если находящейся в этом состоянии конструкции сообщить некоторое небольшое отклонение от начального положения, то по прекращении действия причины, вызвавшей это отклонение, конструкция в исходное положение уже не вернется, но будет способна сохранить приданное ей, благодаря отклонению, новое положение.
Состояние безразличного равновесия, представляющее как бы границу между двумя основными состояниями – устойчивым и неустойчивым, называется критическим состоянием. Нагрузка, при которой конструкция сохраняет состояние безразличного равновесия, называется критической нагрузкой.
Эксперименты показывают, что обычно достаточно немного увеличить нагрузку по сравнению с её критическим значением, чтобы конструкция из-за больших деформаций потеряла свою несущую способность, вышла из строя. В строительной технике потеря устойчивости даже одним элементом конструкции вызывает перераспределение усилий во всей конструкции и нередко влечет к аварии.
Изгиб стержня,связанный с потерей устойчивости, называется продольным изгибом.
Критическая сила. Критическое напряжение
Наименьшая величина сжимающей силы, при которой первоначальная форма равновесия стержня – прямолинейная становится неустойчивой – искривленной, называется критической.
При исследовании устойчивости форм равновесия упругих систем первые шаги были сделаны Эйлером.
В упругой стадии деформирования стержня при напряжениях, не превышающих предел пропорциональности, критическая сила вычисляется по формуле Эйлера:
где Imin – минимальный момент инерции сечения стержня (обусловлено тем, что изгиб стержня происходит в плоскости с наименьшей жесткостью), однако исключения могут быть только в случаях, когда условия закрепления концов стержня различны в разных плоскостях, ℓ — геометрическая длина стержня, μ – коэффициент приведенной длины или коэффициент приведения (зависит от способов закрепления концов стержня), Значения μ приведены под соответствующей схемой закрепления стержней 
Критическое напряжение вычисляется следующим образом
![]() , где
, где ![]() гибкость стержня ,
гибкость стержня ,
а  радиус инерции сечения.
радиус инерции сечения.
Введем понятие предельной гибкости.
Величина λпред зависит только от вида материала: 
Если у стали 3 Е=2∙1011Па, а σпц=200МПа, то предельная гибкость

Для дерева (сосна, ель) предельная гибкость λпред=70, для чугуна λпред=80
Таким образом, для стержней большой гибкости λ≥λпред критическая сила определяется по формуле Эйлера.
В упругопластической стадии деформирования стержня, когда значение гибкости находится в диапазоне λ0≤λ≤λпр, (стержни средней гибкости) расчет проводится по эмпирическим формулам, например, можно использовать формулу Ясинского Ф.С. Значения введенных в нее параметров определены эмпирически для каждого материала.
σк=а-bλ, или Fкр= A(a— bλ)
где a и b – постоянные, определяемые экспериментальным путем (эмпирические коэффициенты).Так, для стали3 а=310МПа, b=1,14МПа.
При значениях гибкости стержня 0≤λ≤λ0 (стержни малой гибкости) потеря устойчивости не наблюдается.
Таким образом, пределы применимости формулы Эйлера — применяется только в зоне упругих деформаций.
Условие устойчивости. Типы задач при расчете на устойчивость. Коэффициент продольного изгиба
Условием устойчивости сжатого стержня является неравенство:

Здесь допускаемое напряжение по устойчивости [σуст] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих факторов:
1) от длины стержня, от размеров и даже от формы поперечных сечений,
2) от способа закрепления концов стержня,
3) от материала стержня.
Как и всякая допускаемая величина, [σуст] определяется отношением опасного для сжатого стержня напряжения к коэффициенту запаса. Для сжатого стержня опасным является так называемое критическое напряжение σкр, при котором стержень теряет устойчивость первоначальной формы равновесия.
Поэтому 
Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷2, то kуст=2÷5.
Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности:![]()
В этом случае  ,
,
где σт – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатие σвс).
Коэффициент φ<1 и потому называется коэффициентом снижения основного допускаемого напряжения, то есть [σ] по прочности, или иначе коэффициентом продольного изгиба.
С учетом сказанного условие устойчивости сжатого стержня принимает вид:

Численные значения коэффициента φ выбираются из таблиц в зависимости от материала и величины гибкости стержня ![]() , где:
, где:
μ – коэффициент приведенной длины (зависит от способов закрепления концов стержня), ℓ — геометрическая длина стержня,
i – радиус инерции поперечного сечения  относительно той из главных центральных осей сечения, вокруг которой будет происходить поворот поперечных сечений после достижения нагрузкой критического значения.
относительно той из главных центральных осей сечения, вокруг которой будет происходить поворот поперечных сечений после достижения нагрузкой критического значения.
Коэффициент φ изменяется в диапазоне 0≤φ≤1, зависит ,как уже говорилось, как от физико-механических свойств материала, так и от гибкости λ. Зависимости между φ и λ для различных материалов представляются обычно в табличной форме с шагом ∆λ=10.
При вычислении значений φ для стержней, имеющих значения гибкости не кратные числу 10, применяется правило линейной интерполяции.
Значения коэффициента φ в зависимости от гибкости λ для материалов

На основании условия устойчивости решаются три вида задач:
- Проверка устойчивости.
- Подбор сечения.
- Определение допускаемой нагрузки (или безопасной нагрузки, или грузоподъемности стержня: [F]=φ[σ]А.
Наиболее сложным оказывается решение задачи о подборе сечения, поскольку необходимая величина площади сечения входит и в левую, и в правую часть условия устойчивости:

Только в правой части этого неравенства площадь сечения находится в неявном виде: она входит в формулу радиуса инерции  , который в свою очередь включен в формулу гибкости
, который в свою очередь включен в формулу гибкости ![]() , от которой зависит значение коэффициента продольного изгиба φ. Поэтому здесь приходится использовать метод проб и ошибок, облеченный в форму способа последовательных приближений:
, от которой зависит значение коэффициента продольного изгиба φ. Поэтому здесь приходится использовать метод проб и ошибок, облеченный в форму способа последовательных приближений:
1 попытка: задаемся φ1 из средней зоны таблицы, находим  , определяем размеры сечения, вычисляем
, определяем размеры сечения, вычисляем  , затем гибкость
, затем гибкость ![]() , по таблице определяем
, по таблице определяем ![]() и сравниваем со значением φ1 . Если
и сравниваем со значением φ1 . Если ![]() , то:
, то:
2 попытка: принимаем  , находим
, находим  , определяем размеры сечения, вычисляем
, определяем размеры сечения, вычисляем  , затем гибкость
, затем гибкость ![]() , по таблице определяем
, по таблице определяем ![]() , и если
, и если ![]() , то:
, то:
3 попытка: принимаем  , находим
, находим  , определяем размеры сечения, вычисляем
, определяем размеры сечения, вычисляем  , затем гибкость
, затем гибкость ![]() , по таблице определяем
, по таблице определяем ![]() , и т.д.
, и т.д.
Процесс приближений продолжается до тех пор, пока разница не окажется менее 5%.
Источник
ФОРМУЛА ЭЙЛЕРА
Если тонкий прямой стержень сжимать вдоль оси, постепенно увеличивая силу Р, то вначале он будет оставаться прямым, но затем при некоторой нагрузке называемой критической, стержень начнет резко изгибаться. Это явление называют потерей устойчивости (рис. 1). При потере устойчивости напряжения быстро возрастают, что может привести к разрушению детали. Для нормальной работы большинства конструкций потеря устойчивости недопустима. Обычно допускаемая нагрузка не превышает
Чтобы найти критическую силу рассмотрим условия, при которых сжатый стержень может находиться в изогнутом состоинии в условиях равновесия (рис. 2). При малых прогибах справедливо обычное уравнение изгиба
или
где
Рис. 14. Области применения приближенного решения для осесимметричной деформации колец: а — кольцо заделано в массивное тело — решение не пригодно; — кольцо оперто и имеет возможность поворота — решение может быть использовано
Общее решение уравнении (1)
для опертого по концам стержня должно удовлетворять граничным условиям что возможно, еслн Стержень может прогнуться только при условии Пока сжимающая сила Р мала, так что величина значение и стержень остается примолинейным. При
стержень может принять помимо прямолинейной формы, котораи становится
Рис. 1. (см. скан) Потеря устойчивости стержня при сжатии
Рис. 2. (см. скан) Осевое сжатие двухопорного стержня
неустойчивой, новую форму равновесия с изогнутой осью. Для определения величины прогиба при необходимо использовать в уравнении изгиба точное выражение кривизны стержня (см. рис. 2)
и учесть изменение расстояния между концами стержня в результате изгиба. При малых прогибах это приводит к выражению
При прогиб отсутствует, но при дальнейшем увеличении силы прогиб очень быстро растет. Так, если сжимающая сила превысит критическую всего на 1,5%, то стержень длиной прогнется на 11 см.
Критическую силу определяют по минимальному моменту инерции сечения. Величина зависит от условий закрепления, характера нагружения и конфигурации сечений стержня.
Из сравнения форм прогибов двухопорного стержня, консольного (рис. 3, а) и с двумя заделанными концами (рис. 3, б) следует, что условия потери устойчивости будут у них одинаковыми, если заменить длину стержня «приведенной» длиной для двухопорного стержня для консольного , а для стержня с заделанными концами
В общем случае формулу Эйлера (3) можно представить в виде
где
Рис. 3. (см. скан) Формы прогибов при по устойчивости стержней
Рис. 4. (см. скан) К общему случаю расчета критической нагрузки
Критической нагрузке соответствует напряжение сжатия
где коэффициент X характеризует приведенную гибкость стержня с учетом условий его опирания и нагружения:
Здесь — радиус инерции поперечного сечения,
С учетом выражения (7) формулу (5) можно записать в виде
ОБЩИЙ СЛУЧАЙ РАСЧЕТА КРИТИЧЕСКОЙ НАГРУЗКИ
Дифференциальное уравнение изгиба (1) можно записать в углах поворота
откуда
При действии на стержень в сечениях нескольких продольных сжимающих сил и распределенной продольной нагрузки (рис. 4)
где
В частном случае, при защемлении стержня в сечении когда
В безразмерном виде
где — значение при — критическое значение одной ил нагрузок или их суммы; значение в некоторой выбранной точке,
заданные отношения нагрузок при потере устойчивости.
Тогда из (11) — (15)
где — интегральный оператор;
Уравнение (16) решают методом последовательных приближений — по функции находят и из условия минимума среднего квадратического отклонения [1] — значение
и
В качестве исходного приближения выбирают функцию, удовлетворяющую кинематическим граничным условиям (для защемленного стержня ).
Пример. Найти коэффициент для консольного стержня постоянного сечения, сжимаемого силой на конце Принимая находим
что мало отличается от точного решения
В общем случае интегралы находят численно. При других граничных условиях меняется только вид оператора (17).
Источник
| ||||
Регистрация: 23.03.2012 Сообщений: 13 | Правильно. Здесь сын ошибок трудных снимает шляпу перед друзьями парадоксов, убирает весь компромат со стола и пытается сформулировать то в чём он пока ещё видит чистую упругую и пластичную красоту. 1. идеальная упругость + малые деформации. Линейная задача. Форма зависит от внешней нагрузки линейно. Есть как минимум два типа расчётов: проверочный — когда конструируем и подбираем требуемую жёсткость и прочность, ………… Это правильно, но из категории «просто добавь момент» и не имеет отношения к решению нелинейной задачи.
| |||
|
Источник
Лекция 12. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Понятие об устойчивости и критической силе. Проектировочный и проверочный расчеты.
В конструкциях и сооружениях большое применение находят детали,
являющиеся относительно длинными и тонкими стержнями, у которых один или
два размера поперечного сечения малы по сравнению с длиной стержня.
Поведение таких стержней под действием осевой сжимающей нагрузки
оказывается принципиально иным, чем при сжатии коротких стержней: при
достижении сжимающей силой F некоторой критической величины, равной Fкр,
прямолинейная форма равновесия длинного стержня оказывается
неустойчивой, и при превышении Fкр стержень начинает интенсильно
искривляется (выпучивается). При этом новым (моментным) равновесным
состоянием упругого длинного становится некоторая новая уже
криволинейная форма. Это явление носит название потери устойчивости.
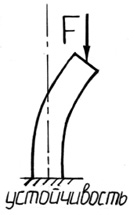
Рис. 37. Потеря устойчивости
Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях.
Критическая сила (Fкр) – нагрузка, превышение которой вызывает
потерю устойчивости первоначальной формы (положения) тела. Условие
устойчивости:
Fmax ≤ Fкр, (25)
Устойчивость сжатого стержня. Задача Эйлера.
При определении критической силы, вызывающей потерю устойчивости
сжатого стержня, предполагается, что стержень идеально прямой и сила F
приложена строго центрально. Задачу о критической нагрузке сжатого
стержня с учетом возможности существования двух форм равновесия при
одном и том же значении силы решил Л. Эйлер в 1744 году.
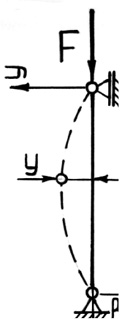
Рис. 38. Сжатый стержень
Рассмотрим шарнирно опертый по концам стержень, сжатый продольной
силой F. Положим, что по какой-то причине стержень получил малое
искривление оси, вследствие чего в нем появился изгибающий момент M:
M = –F•y,
где y – прогиб стержня в произвольном сечении с координатой x.
Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:
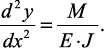 (26)
(26)
Проведя преобразования, можно увидеть, что минимальное значение
критическая сила примет при n = 1 (на длине стержня укладывается одна
полуволна синусоиды) и J = Jmin (стержень искривляется относительно оси
с наименьшим моментом инерции)
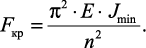 (27)
(27)
Это выражение – формула Эйлера.
Зависимость критической силы от условий закрепления стержня.
Формула Эйлера была получена для, так называемого, основного
случая – в предположении шарнирного опирания стержня по концам. На
практике встречаются и другие случаи закрепления стержня. При этом можно
получить формулу для определения критической силы для каждого из этих
случаев, решая, как в предыдущем параграфе, дифференциальное уравнение
изогнутой оси балки с соответствующими граничными условиями. Но можно
использовать и более простой прием, если вспомнить, что, при потере
устойчивости на длине стержня должна укладываться одна полуволна
синусоиды.
Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.
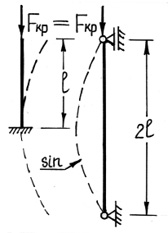
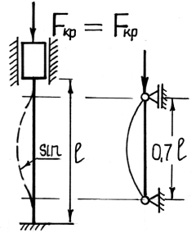
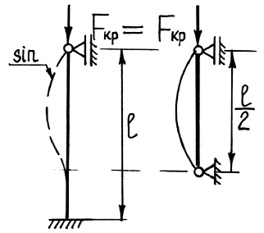
Рис. 39. Различные случаи закрепления стержня
Общая формула Эйлера:
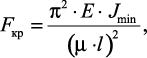 (28)
(28)
где μ·l = lпр – приведенная длина стержня; l – фактическая длина
стержня; μ – коэффициент приведенной длины, показывающий во сколько раз
необходимо изменить длину стержня, чтобы критическая сила для этого
стержня стала равна критической силе для шарнирно опертой балки. (Другая
интерпретация коэффициента приведенной длины: μ показывает, на какой
части длины стержня для данного вида закрепления укладывается одна
полуволна синусоиды при потере устойчивости.)
Таким образом, окончательно условие устойчивости примет вид
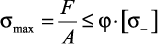 (29)
(29)
Рассмотрим два вида расчета на устойчивость сжатых стержней – проверочный и проектировочный.
Проверочный расчет
Порядок проверочного расчета на устойчивость выглядит так:
– исходя из известных размеров и формы поперечного сечения и условий закрепления стержня, вычисляем гибкость;
– по справочной таблице находим коэффициент понижения допускаемого
напряжения, затем определяем допускаемое напряжение на устойчивость;
– сравниваем максимальное напряжение с допускаемым напряжением на устойчивость.
Проектировочный расчет
При проектировочном расчете (подобрать сечение под заданную
нагрузку) в расчетной формуле имеются две неизвестные величины – искомая
площадь поперечного сечения A и неизвестный коэффициент φ (так как φ
зависит от гибкости стержня, а значит и от неизвестной площади A).
Поэтому при подборе сечения обычно приходится пользоваться методом
последовательных приближений:
– обычно в первой попытке принимают φ1 = 0,5…0,6 и определяют площадь сечения в первом приближении
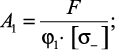
– по найденной площади A1 подбирают сечение и вычисляют гибкость
стержня в первом приближении λ1. Зная λ, находят новое значение φ′1;
– далее, используя найденный φ′1, проверяют условие устойчивости,
и если σmaxmax и [σу] значительно отличаются друг от друга (более чем на
5 %), следует повторить расчет, приняв во второй попытке
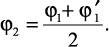
Выбор материала и рациональной формы сечения.
Выбор материала. Так как в формулу Эйлера из всех механических
характеристик входит лишь модуль Юнга, то для повышения устойчивости
стержней большой гибкости нецелесообразно применять высокопрочные
материалы, так как модуль Юнга для всех марок сталей примерно одинаков.
Для стержней малой гибкости применение высокосортных сталей
оправдано, так как с повышением предела текучести у таких сталей
повышаются и критические напряжения, а значит и запас устойчивости.
Форма сечения. При проектировании стержней, работающих на
устойчивость, следует выбирать такую форму сечения, чтобы гибкость
стержня была одинаковой относительно обеих главных осей его сечения
(условие равноустойчивости), а значит максимальный и минимальный моменты
инерции такого сечения должны быть одинаковы Jmax = Jmin.
Кроме того, необходимо стремиться к получению при данной площади
наибольших радиусов инерции. Для этого необходимо выбирать сечения,
большая часть площади которых по возможности была удалена от центра
тяжести (трубчатые, коробчатые сечения).
По степени рациональности известные сечения можно распределить
следующим образом: трубчатое сечение, коробчатое, двутавровое, состоящее
из швеллеров, квадратное, круглое, прямоугольное.
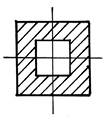
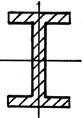
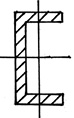
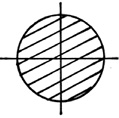
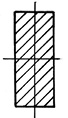
Рис. 40. Поперечные сечения, распределенные по степени рациональности
Источник
