Подобрать сечение стержня на растяжение

где N — продольная растягивающая сила, действующая на стержень;
F — площадь поперечного сечения стержня;
σ — нормальные напряжения, возникающие в рассматриваемом поперечном сечении стержня в ответ на действие растягивающей продольной силы;
Rр — расчетное сопротивление материала стержня растяжению (для некоторых материалов расчетные сопротивления растяжению, сжатию, изгибу и т.п. могут различаться).
Визуально это может выглядеть так:

Рисунок 525.1. Нормальные напряжения при растяжении прямолинейного стержня.
На рисунке 525.1.а) мы видим прямолинейный стержень длиной l, показанный серым цветом, к которому приложена растягивающая сила N. При этом точка приложения силы находится на нейтральной оси стержня, совпадающей с осью х, показанной пунктирной линией.
Для упрощения расчетов заменяем опору А соответствующей опорной реакцией А (рис.525.1.б). Исходя из условий статического равновесия:
∑х = А + N = 0 (149.5.2)
А = — N (525.2)
Это означает, что опорная реакция A равна по значению растягивающей силе N, но направлена в противоположную сторону.
Если взглянуть на эту ситуацию под некоторым углом, то она будет выглядеть так, как показано на рисунке 525.1.в). На этом рисунке мы видим, что нормальные напряжения — это реакция материала на действие растягивающей силы и направлены эти напряжения в сторону, противоположную действию сил. Другими словами нормальные напряжения препятствуют деформации растяжения, и направлены на то, чтобы вернуть материалу исходную форму. Иногда для упрощения восприятия нормальные напряжения, возникающие при растяжении, принято изображать направленными от сечения, как показано на рисунке 525.1.г), а сжимающие напряжения — направленными к сечению. С точки зрения физики такая замена вполне допустима, так как нормальные напряжения (внутренние силы) можно рассматривать как плоскую нагрузку, распределенную по всей площади сечения (внешнюю силу). Как правило растягивающие нормальные напряжения рассматриваются как положительные, а сжимающие — как отрицательные.
Сечение стержня, показанное на рисунке 525.1.в) розовым цветом, является перпендикулярным нейтральной оси стержня и называется поперечным сечением.
Как следует из формулы (525.1) и из приведенного рисунка, длина стержня l на значение нормальных напряжений никак не влияет. А вот параметры поперечного сечения стержня: ширина сечения b и высота сечения h, если сечение прямоугольное, очень даже влияют, так как от этих параметров зависит площадь F поперечного сечения.
Примечание: конечно же поперечное сечение стержня далеко не всегда имеет прямоугольную форму, как показано на рисунке 525.1.в). Поперечное сечение может быть и круглым, и овальным, и ромбическим, и вообще иметь любую сколь угодно сложную форму, тем не менее форма поперечного сечения никак на значение нормальных напряжений не влияет (во всяком случае такое допущение принимается в теории сопротивления материалов), а влияет только площадь сечения, определить которую тем сложнее, чем более сложной является форма поперечного сечения.
Проверить данные постулаты теории сопротивления материалов очень легко и просто. Достаточно взять нитку и попробовать ее разорвать (вариант а)). Затем разорвать нитки с с той же катушки, но б) более короткую и в) более длинную, чем в первом случае. Во всех трех случаях усилие, которое необходимо приложить для разрыва нитки, будет примерно одинаковым.
Но если одну из ниток сложить вдвое и попробовать разорвать, то усилие, необходимое для разрыва нитки, увеличится в 2 раза. Все потому, что условная площадь сечения стержня, работающего на растяжение, увеличится при складывании нитки в 2 раза.
Таким образом известная пословица: «где тонко, там и рвется» в переводе на язык теории сопротивления материалов будет звучать примерно так: «при действии растягивающих нормальных напряжений разрушение материала, обладающего постоянным сопротивлением растяжению по всей длине, будет происходить в сечении с минимальной площадью». Это особенно актуально для стержней с изменяющейся по длине площадью сечения.
С учетом различных факторов формула (525.1) может иметь другой вид:
Nγn/Fn = σ ≤ Rрγs (512.1.2)
где γn — коэффициент надежности по нагрузке (как правило больше единицы), Fn — минимальная площадь сечения (с учетом возможных ослаблений отверстиями, пазами и т.п.), γs — коэффициент условий работы (как правило меньше единицы).
Т.е. теория сопротивления материалов допускает, что нормальные напряжения в стержне могут быть равны расчетному сопротивлению материала на растяжение, умноженному на коэффициент условий работы.
Пример расчета стержня на растяжение
Дано: На стальной стержень (см. рис.525.1.а)) с расчетным сопротивлением Rp = 2250 кг/см2 действует продольная растягивающая сила N = 30 тонн. Коэффициент надежности по нагрузке γn = 1.05, коэффициент условий работы γs = 0.9. Собственным весом стержня в виду его незначительности по сравнению с действующей нагрузкой для упрощения расчетов можно пренебречь. Предполагается, что нагрузка прикладывается по всей площади поперечного сечения стержня, т.е. возникающие нормальные напряжения будут равномерно распределенными по всей площади сечения.
Требуется: Подобрать диаметр стержня.
Решение:
1. Определяем требуемую площадь сечения стержня, преобразовав формулу (525.1.2)
F = Nγn/Rpγs = 30000·1.05/(2250·0.9) = 15.56 см2.
2. Определяем диаметр стержня
d = √4F/п = √4·15.56/3.14 = 4.45 см
Как видим сам расчет занимает гораздо меньше времени, чем описание физических характеристик используемых данных и даже формулировка условия задачи.
Источник



2.4. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ Основной задачей расчета конструкции на растяжение является обеспечение ее прочности в условиях эксплуатации. Условие прочности – оценка прочности элемента конструкции, сводящаяся к сравнению расчетных напряжений с допускаемыми: σ≤рσ[р ]; σ с ≤[ с],σ (2.9) где σр и σс – наибольшие расчетные растягивающие и сжимающие напряжения; [σр] и [σс] – допускаемые напряжения при растяжении и сжатии. Допускаемое напряжение – наибольшее напряжение, которое можно допустить в элементе конструкции при условии его безопасной, долговечной и надежной работы: Здесь σпред – предельное напряжение (состояние), при котором конструкция перестает удовлетворять эксплуатационным требованиям; им мо- гут быть предел текучести, предел прочности, предел выносливости, пре- дел ползучести и др. Для конструкций из пластичных материалов при определении допускаемых напряжений используют предел текучести σт (рис. 2.4, а). Это связано с тем, что в случае его превышения деформации резко возрастают при незначительном увеличении нагрузки и конструкция перестает удовлетворять условиям эксплуатации. Допускаемое напряжение в этом случае определяют как Для хрупких материалов (чугун, бетон, керамика) где σвр и σвс – пределы прочности при растяжении и сжатии (рис. 2.4, б). Здесь [n] – нормативный коэффициент запаса прочности. В зависимости от той предельной характеристики, с которой сравнивают расчетное напряжение σ, различают [nт] – нормативный коэффициент запаса прочности по отношению к пределу текучести σт и [nв] – нормативный коэффициент запаса прочности по отношению к пределу прочности σв. Запас прочности – отношение предельно допустимой теоретической нагрузки к той нагрузке, при которой возможна безопасная работа конструкции с учетом случайных перегрузок, непредвиденных дефектов и недостоверности исходных данных для теоретических расчетов. Нормативные коэффициенты запаса прочности зависят: − от класса конструкции (капитальная, временная), − намечаемого срока эксплуатации, − условий эксплуатации (радиация, коррозия, загнивание), − вида нагружения (статическое, циклическое, ударные нагрузки) − неточности задания величины внешних нагрузок, − неточности расчетных схем и приближенности методов расчета − и других факторов. Нормативный коэффициент запаса прочности не может быть единым на все случаи жизни. В каждой отрасли машиностроения сложились свои подходы, методы проектирования и приемы технологии. В изделиях общего машиностроения принимают [nт] = 1,3 – 2,2; [nв] = 3 – 5. Вероятность выхода из строя приближенно можно оценить с помощью коэффициента запаса в условии прочности: n = 1 соответствует вероятности невыхода из строя 50 %; n = 1,2 соответствует вероятности невыхода из строя 90 %; n = 1,5 соответствует вероятности невыхода из строя 99 %; n = 2 соответствует вероятности невыхода из строя 99,9 %. Для неответственных деталей n = 2 много. Для ответственных – мало. Так для каната подъемного лифта это означает на 1000 подъемов одно падение. При расчете конструкций на прочность встречаются три вида задач, которые вытекают из условия прочности а) поверочный расчет (проверка прочности). Известны усилие N и площадь A. Вычисляют σ = N/A и, сравнивая его с предельным σт или σв (для пластичного и хрупкого материалов соответственно), находят фактический коэффициент запаса прочности который затем сопоставляют с нормативным [n]; б) проектный расчет (подбор сечения). Известны внутреннее усилие N и допускаемое напряжение [σ]. Определяют требуемую площадь поперечного сечения стержня в) определение грузоподъемности (несущей способности). Известны площадь А и допускаемое напряжение [σ]. Вычисляют внутреннее усилие N≤N[ ] = ⋅[σ]A, (2.15) а затем в соответствие со схемой нагружения – величину внешней нагрузки F ≤ [F].
Источник
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:

где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:

Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:

Соответственно, относительную поперечную деформацию определяют по формуле:

При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:

Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:

Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:

Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:

где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):

При проектном расчете определяется площадь опасного сечения стержня:

При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:

Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:

Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Главная
Расчеты на растяжение и сжатие
статически определимых стержневых систем
Пример 1.
Абсолютно
жесткий брус ВС (ЕВС = ) прикреплен в точке С к неподвижному шарниру (см.
рис.), а в точке В поддерживается
стальной тягой АВ. В точке В приложена вертикальная сила F = 20 кН.
Подобрать
сечение тяги АВ и показать перемещение
точки В. Расчетное сопротивление
стали растяжению коэффициент условий работы а модуль упругости
стали тяги АВ –
Решение.
Вырежем
мысленно узел В (рис. б) и составим для него уравнения
равновесия:
откуда находим
откуда
Окончательно
имеем
Следовательно,
брус ВС сжат силой N2, а элемент АВ растянут силой N1.
Подбор сечения
тяги АВ проводим по формуле откуда определяем
Предположим,
что тяга АВ имеет круглое поперечное
сечение, тогда An =
1,44 см2 = , откуда находим r =
0,677 смиd = 1,35 см.
Определим
удлинения стержней АВ и СВ:
Таким образом, точка В переместится в точку В/
по дуге окружности радиусом , причем расстояние между точками А и В/будет равно
Пример 2.
Определить из расчетов на прочность и жесткость
допускаемую силу F, если [] = 120 МПа, [] = 1,7 мм, А1 = 2А, А2 = А = 5 см2, l1 = l2 = l = 1 м, Е = 200 ГПа.
Р е ш е н и е.
1. Определение усилий в стержнях.
Из условия равновесия бруса АС имеем
, , ;
, , .
2. Расчет на прочность.
Находим напряжения в
стержнях
,
.
Как видим, наиболее
нагруженным является 2-й стержень, прочность которого предопределяет прочность
всей конструкции в целом. Из условия прочности находим = 30 кН.
3. Расчет на жесткость.
Вычисляем деформации
стержней
,
,
а по ним перемещение точки С. Из подобия треугольников В1А1В2 и С1А1С2 имеем:
В1В2/А1В2 = С1С2/А1С2 или ,
откуда .
Записываем условие жесткости ,
откуда = 200×109×5×10-4×1,7×10-3/(8,5×1)= 20 кН.
Допускаемая нагрузка из расчета на жесткость
получилась меньше, чем из расчета на прочность, поэтому ее и принимаем в качестве окончательной, т.е.
кН.
Пример 3.
К двум
одинаковым стержням приложена сила F.
Установить, при каком угле конструкция будет
иметь наименьший вес?
Р е ш е н и е.
Вес
конструкции является функцией угла , т.е. .
Нам необходимо установить такой угол, при котором
функция принимает минимальное значение. В теории оптимального
проектирования она называется целевой функцией.
Для
определения веса стержневой системы нужно знать площади сечений стержней. Из
условия равновесия узла С находим
усилия в стержнях:
, , ,
а из условия
прочности – площади их поперечных сечений:
, откуда .
Учитывая, что
длины стержней , находим вес конструкции (целевую функцию):
.
Функция принимает минимальное
значение, когда
, откуда и .
Определение грузоподъемности
статически определимой конструкции, работающей на растяжение-сжатие. Расчет по
допускаемым напряжениям
При таком
подходе несущая способность конструкции отождествляется с несущей способностью
наиболее нагруженного элемента. Последовательность расчета при этом выглядит
следующим образом.
Составляются уравнения статики и по числу лишних неизвестных –
дополнительные уравнения совместности деформаций. Решая полученную систему,
определяют усилия в стержнях и связанные с ними напряжения. Из сопоставления
напряжений в наиболее нагруженном элементе с допустимой величиной делается
заключение о надежности конструкции либо определяются искомые величины (размеры
сечения стержней, допускаемая нагрузка).
Пример 4.
Конструкция,
состоящая из стержней, соединенных шарнирами, загружена силой F (см. рис. 1). Сечения стержней – из
прокатной стали и площади сечений можно найти по таблицам сортамента прокатной
стали. Цель расчета:
1. определить
значение допускаемой нагрузки;
2. найти
перемещение узла С.
Рис.1
Решение.
Для
определения усилий используем метод сечений. Для этого нарисуем план сил
(рис.2): рассечем деформируемые стержни конструкции и отброшенные части
стержней заменим продольными силами N1 и N2 .
Рис.2
Из уравнений
равновесия отсеченной части конструкции найдем продольные силы в стержнях:
и .
Знак минус показывает,
что направление усилия в стержне 2 противоположно показанному на плане сил,
т.е. стержень 2 сжат.
Определим
напряжения по и выберем наиболее напряженный стержень (допустим, что в рассматриваемой задаче
это будет стержень 1).
Из условия прочности этого стержня получим значение
допускаемой нагрузки:
, .
Найдем
перемещение узла С,
построив план перемещений (рис.3).
Рис.3
Предварительно
найдем абсолютные деформации стержней и по формуле . В
рассматриваемой задаче растянутый стержень 1 будет удлиняться, а сжатый
стержень 2 – укорачиваться. Для построения плана перемещений нарисуем схему
конструкции в масштабе и отложим отрезки и вдоль оси каждого
стержня, выбрав масштаб для деформаций так, чтобы картинка плана перемещений
была наглядной. В процессе деформации стержни поворачиваются относительно точек
А и В по дугам. Из-за малости деформаций эти дуги заменяем
касательными, т. е. перпендикулярами к направлениям стержней (отрезки и на плане перемещений).
На пересечении дуг (перпендикуляров к направлениям стержней) находится новое
положение узла C после деформации –
точка на плане перемещений.
Вертикальное и горизонтальное перемещение узла C допускается определять по масштабу, не делая сложных
геометрических выкладок.
Примечание. Если конструкция имеет
абсолютно жесткий стержень, то принцип
построения плана перемещений тот же. Все точки абсолютно жесткого стержня могут
перемещаться только по дугам (перпендикулярам к направлению стержня), поворачиваясь
вокруг неподвижного шарнира. Например, если стержень АС на плане перемещений считать абсолютно жестким, то точка Спереместится в положение и горизонтальное
перемещение узла С будет равно нулю.
Пример 5.
Для схемы, изображенной на рис.1 необходимо:
Рис.1
1) Определить площадь поперечного сечения стержней при действии силы F и подобрать угловую равнополочную
или неравнополочную сталь, при условии, что поперечное
сечение одного из стержней в два раза больше, чем другого.
2) Определить напряжения в стержнях:
— от действия силы F;
— от неточности монтажа, если считать, что один из стержней выполнен
короче на величину ;
— от изменения температуры.
3) Определить суммарные напряжения от действия внешних сил, от неточности
монтажа и от изменения температуры.
4) Подсчитать недонапряжения или перенапряжения
в стержнях.
Дано: F=100 кН, а =
1,2м, b = 0,8м, = 0,2мм, = 20°С, Е = 2×105МПа,
= 125×10-71/гр, [] = 100 МПа.
Решение.
Определим необходимую по условию прочности площадь поперечного сечения
стержней.
1) Находим степень статической неопределимости.
2.1) Статическая сторона задачи
; ;
; ;
; .
2.2) Геометрическая сторона задачи (рис.2)
~Þ
; ; ;
2.3) Физическая сторона задачи
;
Рис.2
2.4) Синтез
Подставим выражения, полученные в физической стороне задачи, в выражения
из геометрической стороны задачи и приведем подобные.
Решим совместно систему уравнений, составленную из полученного выражения
для N1 и уравнения моментов из статической стороны
задачи.
2.5) Определяем площадь поперечного сечения стержней
Определим, какой из стержней нагружен сильнее.
;
Второй стержень является более нагруженным, так как , поэтому запишем для него условие прочности и
определим площадь поперечного сечения.
Подбираем по справочнику угловую равнополочную сталь № 70´5
ГОСТ8509-86 (SТ= 6,86 см2).
2.6) Определяем напряжения в стержнях от внешних сил
Первый стержень работает на сжатие, а второй – на растяжение.
3) Определим напряжения в стержнях от неточности монтажа
Будем считать, что короткий стержень выполнен короче на величину (см.рис.3).
Рис.3
3.1) Статическая сторона задачи
; ;
; ;
; .
3.2) Геометрическая сторона задачи
~Þ
; ; ;
3.3) Физическая сторона задачи
;
3.4) Синтез
Подставим в полученное выражение данные из условия задачи и получим:
3.5) Определим напряжения в стержнях
Оба стержня работают на растяжение.
4) Определим напряжения в стержнях от изменения температуры (см. рис. 4).
Рис.4
Будем считать, что температура системы повышается. Тогда оба стержня будут
удлиняться от повышения температуры. При удлинении стержней, они будут
воздействовать друг на друга через недеформируемый стержень АС. Вследствие этого, в обоих стержнях
будут возникать дополнительные силы сжатия.
4.1) Статическая сторона задачи
; ;
; ;
; .
4.2) Геометрическая сторона задачи
~Þ
; ; ;
4.3) Физическая сторона задачи
;
.
4.4) Синтез
Решив уравнение, получим .
4.5) Определим напряжения в стержнях
Оба стержня работают на сжатие.
5) Определим суммарные напряжения в стержнях
6) Найдем недонапряжения или перенапряжения в
стержнях
— недонапряжение
— недонапряжение.
Пример 6.
Дано: Сила F= 100 кН;
расчетное сопротивление стали R =160 МПа; модуль упругости E=2∙105
МПа(рис. а)
Требуется:
1. Определить
усилия в стержнях.
2. Подобрать
размеры поперечных сечений стержней. Стержень 1 стальной, круглого поперечного
сечения, стержень 2 стальной квадратного сечения.
3. Вычислить
удлинения (укорочения) стержней и построить план перемещений.
4. Определить
перемещение узла.
а)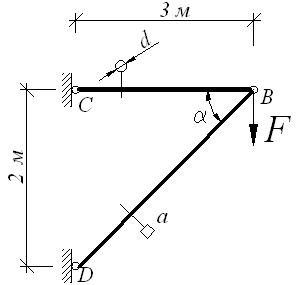 б)
б)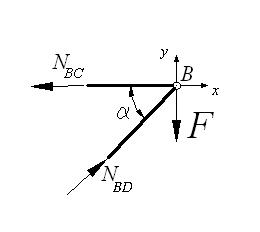
в)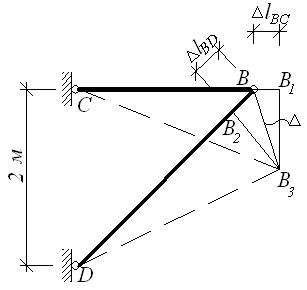 г)
г)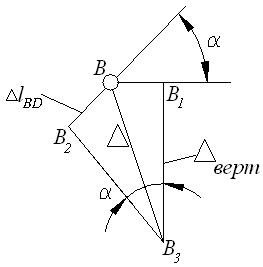
Решение.
Мысленно
вырезаем узел В,
действие отброшенной части кронштейна заменяем искомыми внутренними усилиями.
Для полученной плоской системы сходящихся сил составим уравнения равновесия
(рис. б)
Решив
уравнения, найдем внутренние усилия NBD и NBC
Полученные
положительные значения внутренних усилий показывают, что предварительно
выбранные направления усилий оказались верными, стержень BC
растягивается, а стержень BD сжимается.
Диаметр
стержня BC находим из условия прочности:
где,
откуда .
Размеры поперечного сечения стержня BD определим на условия
прочности:
где ABD = a2,
откуда .
Перемещение
узла В
найдем с помощью графоаналитического метода, для чего вычислим, используя закон
Гука, абсолютные деформации стержней ВС
и BD, предполагая их свободными в точке В:
где
Положение узла В после деформации стержней
определится в результате построения
деформационного треугольника по сторонам и .
Стержень ВС удлинился на величину , концевое сечение
переместилось в точку В1. Радиусом, равным СВ1проведем из точки С
дугу окружности. Так как перемещения малы, то дугу можно заменить касательной,
проведенной через В1
перпендикулярно оси стерня ВС
(рисунок 1, в).
Стержень BD укоротился на , и концевое сечение переместилось в точку В2.
Заменяя дугу, описанную из точки D радиусом DB2касательной,
проведенной через В2перпендикулярно оси стержня BD, получим на
пересечении перпендикуляров точку В3
— новое положение узла В. Соединив
точку В с В3 найдем перемещение узла В. На рисунке 1, в план перемещений изображен в увеличенном масштабе. План
перемещений рекомендуется строить отдельно, как показано на рисунке 1, г. Из него следует, что горизонтальная
составляющая перемещения узла
В равна:
см.
Вертикальную
составляющую перемещения узла
В легко найти,
воспользовавшись теоремой аналитической геометрии – проекция замыкающей на
любую ось равна алгебраической сумме проекций составляющих на ту же ось. Принимая за ось проекций направление получим:
;
откуда .
Знак учтен при построении
плана перемещений. Полное перемещение узла Вбудет равно:
.
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Строительная механика
Прикладная механика Детали машин
Теория машин и механизмов
Источник
