Перемещение при растяжении и сжатии перемещение
В подавляющем большинстве случаев элементы конструкций работают при напряжениях, когда материал остается упругим и справедлив закон Гука (1.7.1). Ситуации, при которых появление неупругих деформаций неизбежно, возможно или даже желательно, встречаются чаще всего в технологии машиностроения и требуют особого рассмотрения. Мы будем иметь дело в основном с упругими телами. Для упругого стержня, используя закон Гука (1.7.1) и формулу (1.6.2), получим
Произведение называется жесткостью стержня при растяжении-сжатии. Далее, из определения (1.6.2) и формулы (2.2.1) вытекает:
В том случае, когда продольная сила и (или) жесткость стержня изменяются по его длине, формулу (2.2.2) следует применить к элементу бесконечно малой длины Тогда для подсчета абсолютной деформации стержня нужно применить операцию интегрирования по его длине I:
Если на каждом /-м участке стержня подынтегральная функция в формуле (2.2.3) остается постоянной, интегрирование можно заменить суммированием:
где п — число участков стержня.
Формулы (2.2.2)-(2.2.4) позволяют определить перемещение любого поперечного сечения, вызванное деформацией стержня. Очевидно, это перемещение численно равно абсолютной деформации части стержня, заключенной между неподвижным (закрепленным) и рассматриваемым сечениями.
Рис. 2.3
Пример. Для ступенчатого стержня, изображенного на рис. 2.3, а, требуется выявить закон изменения нормальных сил, напряжений и перемещений но длине стержня при следующих данных: материал — сталь, Е = 2 105 МПа; Рх = Р3 = 50 кН, Р2 = 30 кН; Р = 2 см2, I — 1 м. Собственный вес стержня не учитывать.
Решение. Разобьем стержень на участки, принимая за их границы его концы, а также сечения, в которых приложены сосредоточенные силы или имеет место скачкообразное изменение площади поперечного сечения. Пронумеруем участки римскими цифрами (рис. 2.3, а). Для определения нормальных сил применим метод сечений.
На участке I, заключенном между сечениями а и Ь, условие равновесия нижней отсеченной части стержня имеет вид
где верхний индекс I отмечает принадлежность сечения участку I. Отсюда получим
Далее проведем поперечное сечение на участке II между точками Ь и с. Имеем
Наконец, на участке III (сс1) получим
По найденным значениям на рис. 2.3, б построена эпюра нормальных сил.
Для построения эпюры нормальных напряжений вычислим по формуле (1.8.1) напряжения в поперечных сечениях на каждом участке стержня:
на участке аЬ
Эпюра нормальных напряжений, построенная по вычисленным значениям, изображена на рис. 2.3, в.
Определим, на какую величину 5 переместится каждое сечение стержня в направлении его оси. Учитывая, что сечение с1 неподвижно, приходим к выводу, что перемещение сечения с координатой г3 на третьем участке равно абсолютной деформации части стержня, заключенной между заделкой (с1) и сечением с координатой г3. Следовательно, согласно формуле (1.9.2) имеем:
Полученная зависимость — линейная. Для построения эпюры вычислим перемещения на концах участка III:
в сечении й:
в сечении с:
Отрицательный знак указывает на то, что сечение с перемещается противоположно направлению оси 23. Физически это означает, что на участке ей имеет место сжатие стержня. По вычисленным значениям строится эпюра перемещений сечений Ш-го участка (рис. 2.3, г).
Чтобы построить эпюру перемещений сечений второго участка, проведем сечение, определяемое координатой г2
(см. рис. 2.3, а), отсчитываемой от границы участков III и II. Очевидно, что перемещение этого сечения складывается из перемещения сечения с и абсолютной деформации той части стержня, которая заключена между сечением с и сечением с координатой г2. Из сказанного вытекает:
Здесь через 5(с) обозначено перемещение сечения с. Полагая в последней формуле г2 — 0,61, вычислим перемещение сечения Ь:
По значениям перемещений сечений сибна рис. 2.3, г построена эпюра б на участке И. Выбирая произвольное сечение гх на первом участке, для его перемещения получим:
Пользуясь этой формулой, подсчитаем перемещение свободного конца стержня:
Откладывая вычисленное значение в сечении а, заканчиваем построение эпюры перемещений (см. рис. 2.3, г).
Источник
НАПРЯЖЕНИЯ ПРИ РАСТЯЖЕНИИ (СЖАТИИ) ПРИЗМАТИЧЕСКИХ СТЕРЖНЕЙ. РАСЧЕТ НА ПРОЧНОСТЬ
Переходя к изучению введенных основных видов деформации стержней, ограничимся рассмотрением стержней постоянного поперечного сечения с прямолинейной осью, т. е. призматических стержней. Начнем с деформации растяжения (сжатия).
Напомним, что под растяжением (сжатием) понимают такой вид деформации стержня, при котором в его поперечном сечении возникает лишь один внутренний силовой фактор продольная сила Nz. Поскольку продольная сила численно равна сумме проекций, приложенных к одной из отсеченных частей внешних сил на ось стержня (для прямолинейного стержня она совпадает в каждом сечении с осью Oz), то растяжение (сжатие) имеет место, если все внешние силы, действующие по одну сторону от данного поперечного сечения, сводятся к равнодействующей, направленной вдоль оси стержня (рис. 1). Одна и та же продольная сила Nz при действии на различные части стержня (левую или правую) имеет противоположные направления. Знак Nz зависит от характера вызываемой ею деформации. Продольная сила считается положительной, если вызывает растяжение элемента (рис. 2, а), и она отрицательна, если вызывает сжатие (рис. 2,б).
| Рис.1. Расчетная схема | Рис.2. а) Растяжение и б) сжатие |
Для того, чтобы сформулировать предпосылки теории растяжения (сжатия) призматического стержня, обратимся к эксперименту. Представим себе стержень, изготовленный из какого-либо податливого материала (например, резины), на боковую поверхность которого нанесена система продольных и поперечных рисок (рис. 3, а). Эта ортогональная система рисок остается таковой и после приложения растягивающей нагрузки (рис. 3, б). Поскольку поперечные риски являются следами поперечных сечений на поверхности стержня и остаются прямыми и перпендикулярными к оси стержня то это свидетельствует о выполнении гипотезы плоских сечений (Бернулли). С учетом гипотезы об отсутствии поперечного взаимодействия продольных волокон приходим к выводу, что деформация растяжения стержня сводится к одноосному растяжению его продольных волокон, и в поперечном сечении стержня возникают лишь нормальные напряжения а (рис. 4), индекс г у которых опускаем. Ортогональность продольных и поперечных рисок свидетельствует также об отсутствии сдвигов, а, следовательно, и связанных с ними касательных напряжений т в поперечных и продольных сечениях стержня.
| Рис.3. Модель растянутого стержня | Рис.4. Связь напряжения и усилия |
Тогда продольная сила Nz равная сумме проекции внутренних сил, действующих в данном поперечном сечении площадью F (рис. 4) очевидно будет равна
.
Это соотношение является уравнением равновесия статики, связывающим продольную силу Nz, и нормальное напряжение , которое в общем случае является функцией координат х и у и поэтому не может быть найдено из одного лишь 1 уравнения статики. Таким образом, задача определения напряжений даже в самом простом случае деформирования стержня (растяжении или сжатии) оказывается статически неопределимой.
Необходимое для решения этой задачи дополнительное уравнение вытекает из гипотезы плоских сечений. Поскольку поперечные сечения стержня, оставаясь плоскими и перпендикулярными к оси стержня, в процессе деформирования лишь поступательно перемещаются вдоль оси стержня (что приводит к одинаковому удлинению всех продольных волокон), то приходим к уравнению =const, из которого ввиду однозначности связи и (для линейно-упругого материала этозакон Гука: .) вытекает, что
Решая совместно уравнения получим, что или
Таким образом, при растяжении (сжатии) призматического стержня нормальные напряжения равномерно распределены по поперечному сечению, а касательные напряжения в сечениях отсутствуют, что является следствием гипотезы плоских сечений. Указанное, несмотря на, казалось бы, очевидность и простоту, является фундаментальным результатом, справедливым, строго говоря, лишь для призматического стержня. Однако в инженерной практике его используют и для приближенной оценки нормальных напряжений в стержнях переменного сечения. При этом, чтобы погрешность формулы была невелика, необходимо, чтобы площадь поперечного сечения стержня изменялась достаточно плавно вдоль его оси.
Условие прочности при растяжении (сжатии) призматического стержня для стержня из пластического материала (т. е. материала, одинаково работающего на растяжение и сжатие) будет иметь вид:
(1) |
где допускаемое напряжение. Напряжение в условии (1) подставляется по модулю, так как знак в этом случае роли не играет. Для стержней из хрупких материалов, неодинаково сопротивляющихся растяжению и сжатию, знак напряжения имеет принципиальное значение, и условие прочности приходится формулировать отдельно для растяжения и сжатия
где и напряжения растяжения и сжатия, а и ответствующие им допускаемые напряжения.
В практике инженерных расчетов, исходя из условия прочности, решаются три основные задачи механики материалов конструкций. В применении к случаю растяжения (сжатия) призматического стержня эти задачи формулируются следующим образом.
Проверка прочности (поверочный расчет). Этот расчет проводится, если нагрузка (в нашем случае ее представляет Nz), сечение стержня F и его материал заданы.
Необходимо убедиться, что выполняется условие прочности
Проверочный расчет заключается в том, что определяется фактический коэффициент запаса прочности п и сравнивается с нормативным коэффициентом запаса [n]:
где предельное (или опасное) напряжение, т. е. напряжение, вызывающее отказ элемента конструкции (напомним, что, например, для стержня из пластичного материала этопредел текучести или условный предел текучести ).
Подбор сечения (проектный расчет). В этом расчете по Заданной нагрузке (Nz) определяются размеры поперечного сечения стержня (F) из заданного материала ( дано). Минимальное значение F получим, если в условии прочности (1) принять знак равенства:
Определение допускаемой нагрузки, то есть максимального значения нагрузки, которое допускает данный элемент конструкции (F и даны) при выполнении условия прочности.
ПОНЯТИЕ О КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ, ПРИНЦИП СЕН-ВЕНАНА
Даже для призматического стержня равномерное распределение напряжений по поперечному сечению не всегда имеет место. Так, отклонения от равномерного распределения напряжений наблюдаются в окрестности сечений, содержащих вырезы, выточки, отверстия, трещины, в местах резкого изменения поперечного сечения, а также в местах приложения сосредоточенных сил и т. п. Неравномерное распределение напряжений в указанных местах является следствием искажения плоскостей поперечных сечений или их депланации.
Поясним это явление на примере подверженной растяжению полосы из податливого материала с круговым отверстием, на поверхности которой нанесены продольные и поперечные риски (рис. 5, а). В зоне отверстия имеет место депланация поперечных сечений, вызванная неравномерным растяжением продольных волокон (рис.5, б). При этом наибольшие удлинения и соответственно напряжения max получают волокна возле отверстия. Такое местное увеличение напряжений возле вырезов, выточек, отверстий и т. п., а также в местах приложения сосредоточенных сил, называется у концентрацией напряжений, а источники концентрации напряжений (вырезы, выточки, отверстия и т. п.) получили название концентраторов напряжений.
Рис.5. Концентрация напряжений: а) исходное состояние, б) деформированное состояние, в) распространение напряжений
Рассмотренными методами механики деформированного тела, опирающимися на гипотезу плоских сечений, задачи о распределении напряжений в зонах концентрации напряжений не решаются. Такие задачи решаются методами теории упругости или исследуются экспериментально. При этом для практических расчетов вводится так называемый теоретический коэффициент концентрации напряжений , представляющий собой отношение максимальных max и номинальных напряжений: , где номинальные напряжения определяются без учета концентрации напряжений. В приведенном примере растяжения полосы с отверстием , a Fnt площадь поперечного сечения полосы, уменьшенная за счет отверстия («нетто»). Таким образом, играют роль поправочных коэффициентов.
Однако, как показали эксперименты и точные решения задач теории упругости, местные отклонения от равномерного распределения напряжений, вызванные концентрацией напряжений, быстро затухают по мере удаления от сечения с концентратором, и на расстояниях порядка ширины сечения распределение напряжений можно считать практически равномерным (рис. 5, в). Отмеченное свойство является частным случаем широко используемого практически во всех разделах механики деформируемого твердого тела (в том числе и теории упругости) принципа Сен-Венана
ОПРЕДЕЛЕНИЕ ДЕФОРМАЦИЙ И ПЕРЕМЕЩЕНИЙ
Определим упругие деформации стержня предполагая, что изменение его длины при растяжении , называемое абсолютной продольной деформацией или удлинением, мало по сравнению с его первоначальной длиной . Тогда относительная продольная деформация будет равна
Учитывая, что согласно закону Гука для одноосного растяжения (сжатия)
,
где Е;модуль продольной упругости материала стержня, а нормальные напряжения определяются по формуле (в нашем случае Nz=P),для абсолютной деформации получаем
(2) |
Произведение EF принято называть жесткостью поперечного сечения стержня при растяжении (сжатии), так как удлинение обратно пропорционально EF.
Рис.6. Модели продольной и поперечной деформаций
Как показывают эксперименты, при растяжении стержня размеры его поперечного сечения уменьшаются (рис. 6), а при сжатии увеличиваются. Это явление получило название эффекта Пуассона.
По аналогии с продольной деформацией изменение размеров поперечного сечения (на рис. 6 ) будем называть абсолютной поперечной деформацией, а относительной поперечной деформацией. Относительные продольная и поперечная деформации, имеющие противоположные знаки, связаны между собой коэффициентом , являющимся константой материала и называемым коэффициентом поперечной деформации или коэффициентом Пуассона:
Как известно, для изотропного материала .
Формула (2) для удлинения стержня применима только в случае, когда по длине стержня ни жесткость поперечного сечения, ни продольная сила не изменяются (EF=const, Nz =const). Удлинение стержня со ступенчатым изменением EF и Nz (рис. 7) может быть определено как сумма удлинений ступеней, у которых EF и Nz постоянны:
(индекс k у модуля продольной упругости означает, что участки стержня могут быть изготовлены из различных материалов). В случае, когда Nz и EF меняются по длине стержня l непрерывно и их можно считать постоянными лишь в пределах ступеней длиной dz, обобщая формулу эту, получаем
В качестве тестов для практики расчетов определенных интегралов рекомендую воспользоваться системой входных тестов Т-5, указанных в ПРИЛОЖЕНИИ.
Рис.7. Ступенчатый брус
С упругими продольными деформациями стержня при растяжении (сжатии) связаны продольные перемещения его сечений. На рис. 8 приведены три случая определения таких перемещений, откуда видно, что перемещения поперечных сечений численно равны удлинениям заштрихованных частей стержня:
- перемещение свободного торцевого сечения 11 при неподвижном другом торцевом сечении (рис. 8, а) численно равно удлинению стержня;
- перемещение промежуточного сечения 22 (рис. 8, б) численно равно удлинению части стержня, заключенной между данным сечением и сечением неподвижным;
- взаимное перемещение сечений 33 и 44 (рис, 8, в) численно равно удлинению части стержня, заключенной между этими сечениями.
Рис.8. Модели перемещений
НАПРЯЖЕННОЕ СОСТОЯНИЕ ПРИ РАСТЯЖЕНИИ (СЖАТИИ)
Напряженное состояние при растяжении стержня является одноосным (рис. 9, а). Поскольку на поперечных и продольных площадках касательные напряжения не возникают, то эти площадки являются главными. Причем в случае растяжения , а в случае сжатия .
Рис.9. Напряженное состояние: а ) исходный элемент, б ) компоненты напряжений
Напряжения на площадках, наклоненных к оси стержня под углом , определяются по формулам для упрощенного плоского напряженного состояния:
Площадки с экстремальными касательными напряжениями (рис. 9, б), как известно, наклонены по отношению к исходным под углами (следует и из формулы для ) и равны .
Именно с действием экстремальных связывается появление на боковой поверхности образца из малоуглеродистой стали, испытываемого на растяжение, линий скольжения, ориентированных под углом к оси образца. На площадках с экстремальными действуют и нормальные напряжения, равные .
Дальше…
Источник
Если нормальная
сила и поперечное сечение меняются по
длине ступенчато, то стержень надо
разбить на участки, так чтобы в пределах
каждого участка
![]()
и
![]()
были постоянны, определить удлинение
каждого из участков и тогда полное
удлинение стержня будет равняться
алгебраической сумме, (знак определяется
знаком
![]() )
)
удлинений участков.
Е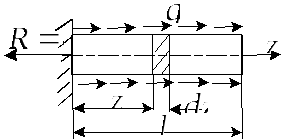 сли
сли
же напряженное состояние в стержне
неоднородно, то выделив малый элемент
длиной
![]() определим
определим
его удлинение
![]() ,
,
Здесь
![]()
и
![]()
рассматривается как функции z.
Полное удлинение стержня будет равно:
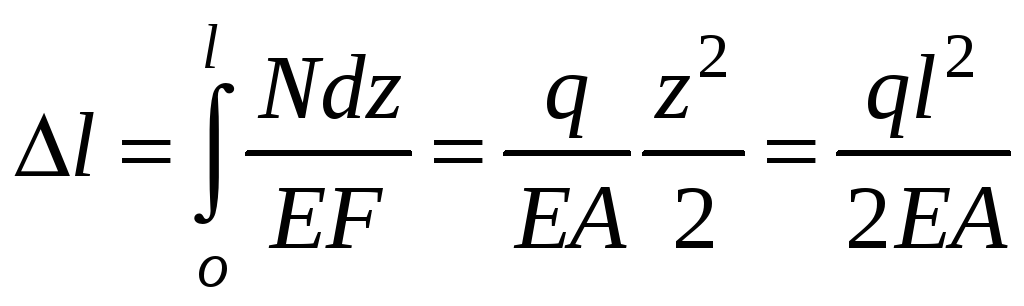
16)
Закон парности касательных напряжений (из напряжений по косым площадкам)
Выясним, каковы
касательные напряжения по площадке
перпендикулярной данной, т.е. задаваемой
углом
![]()
![]() т.е.
т.е.
![]()
Знак
“минус” указывает на то, что касательные
напряжения на взаимно перпендикулярных
площадках направлены либо к ребру между
площадками либо от ребра. Таким образом
имеет место
закон парности касательных напряжений.
Касательные
напряжения по взаимно перпендикулярным
площадкам равны по величине и направлены
как было указано выше.
17)
Расчёты на прочность (проектировочный, проверочный, определение несущей способности)

18)
Напряженное состояние при растяжении и сжатии (напряжения по косым площадкам)
Во вводной лекции
мы уже упоминали о напряженном состоянии
в точке и в частности, говорили, что
знать напряженное состояние в точке –
это уметь вычислить напряжения по любой
площадке, проходящей через данную точку.
Теперь уже мы рассмотрим этот вопрос в
случае, когда исследуемая точка
принадлежит растянутому или сжатому
стержню.
П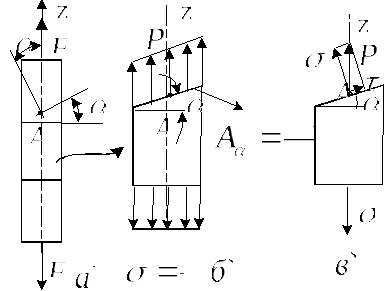 усть
усть
стержень растянут силой F
и в поперечных сечениях стержня, как мы
знаем, возникают нормальные напряжения
равные
![]() ,
,
где А — площадь поперечного сечения.
Проведем через
исследуемую точку А произвольное
сечение, положение которого задается
углом
![]()
между осью стержня и внешней нормалью
к сечению. Кроме того, проведем еще
поперечное сечение. Выделим с помощью
указанных сечений элемент и рассмотрим
равновесие данного элемента.
По наклонной
площадке действует полное напряжение
![]() .
.
проектируя силы, действующие на элемент
на ось стержня, получаем
![]()
![]()
Разлагая
![]()
на нормальное
![]()
и касательное напряжение, получаем
![]()
![]()
Переходя к функциям
угла
![]()
имеем
![]()
Уравнения (5) дают
возможность вычислить напряжения по
любым площадкам, проходящим через данную
точку, т.е. определяют напряженное
состояние при растяжении и сжатии.
Очевидно, что касательные напряжения
обращаются в нуль по двум площадкам
![]()
(поперечное сечение) и
![]()
(продольное сечение). Площадки, по которым
касательные напряжения равны нулю,
называются главными площадками, а
нормальные напряжения, действующие по
ним, главными напряжениями.
Очевидно, что одно
из главных напряжений, действующее в
поперечном сечении —
![]()
является максимальным по модулю, что
обосновывает использование формулы
(1), как основной расчетной формулы при
растяжении, сжатии, а другое главное
напряжение, действующее в продольных
площадках рано нулю. Таким образом,
продольные площадки свободны от
напряжений.
Из второго уравнения
(5) видно, что максимальные касательные
напряжения возникают по площадкам,
наклоненным к оси на угол
![]() ,
,
и равняются по величине
![]()
Максимальные
касательные напряжения являются причиной
разрушения образцов из хрупких материалов,
испытываемых на сжатие.
19)_А
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
