Объемная деформация при растяжении
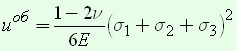
Объемным напряженным состоянием называют напряженное состояние, которое можно представить в виде трех ненулевых главных напряжений. Это напряженное состояние является общим случаем напряженного состояния тела в точке.
Обобщенный закон Гука
Напомним, что при одноосному растяжению или сжатию возникают деформации – продольные (в направлении действия силы) $varepsilon = sigma /E$ и поперечные (в двух других перпендикулярных направлениях) $varepsilon ‘ = — nu cdot varepsilon = — nu sigma /E$.
В случае действия трех главных напряжений ${sigma _1}$, ${sigma _2}$ и ${sigma _3}$ от каждого из них будут возникать продольные и поперечные деформации. Например, от напряжения ${sigma _2}$ будет возникать продольная деформация в направлении 2, которая равна ${varepsilon _2} = {sigma _2}/E$ и поперечные деформации в направлениях 1 и 3 ${varepsilon _1} = {varepsilon _3} = — nu cdot {sigma _2}/E$. Таким образом, деформации в направлении главных осей от системы трех главных напряжений будут определяться так
$begin{gathered} {varepsilon _1} = frac{1}{E}left( {{sigma _1} — nu ({sigma _2} + {sigma _3})} right) hfill \ {varepsilon _2} = frac{1}{E}left( {{sigma _2} — nu ({sigma _1} + {sigma _3})} right) hfill \ {varepsilon _3} = frac{1}{E}left( {{sigma _3} — nu ({sigma _1} + {sigma _2})} right) hfill \ end{gathered} $ – обобщенный закон Гука.
Объемная деформация. Объемный закон Гука
Определим изменение объема тела, которое находится в условиях объемного напряженного состояния.
Объем элементарного куба сторонами $dx$, $dy$ и $d$
${V_0} = dx cdot dy cdot d$.
После деформации, когда длина сторон куба изменилась на величину $Delta x$, $Delta y$ и $Delta z$, об’ем
[begin{gathered} {V_1} = (dx + Delta x) cdot (dy + Delta y) cdot (dz + Delta z) = hfill \ dx cdot dy cdot d + dx cdot dy cdot Delta z + dx cdot Delta y cdot d + underline {underline {dx cdot Delta y cdot Delta z} } + hfill \ + Delta x cdot dy cdot d + underline {underline {Delta x cdot dy cdot Delta z} } + underline {underline {Delta x cdot Delta y cdot d} } + underline {underline {underline {Delta x cdot Delta y cdot Delta z} } } hfill \ end{gathered} ]
Поскольку удлинения являются ничтожно малыми по сравнению с размерами элемента (например, $Delta x < < dx$), то в данной формуле можно пренебречь слагаемыми, которые являются бесконечно малыми второго и третьего порядка (подчеркнуты).
Абсолютное изменение о’объема
[Delta V = {V_1} — {V_0} = dx cdot dy cdot Delta z + dx cdot Delta y cdot d + Delta x cdot dy cdot d]
Относительное изменение о’объема
[{varepsilon _v} = frac{{Delta V}}{{{V_0}}} = frac{{dx cdot dy cdot Delta z + dx cdot Delta y cdot d + Delta x cdot dy cdot d}}{{dx cdot dy cdot d}} = frac{{Delta x}}{{dx}} + frac{{Delta y}}{{dy}} + frac{{Delta z}}{{d}} = {varepsilon _1} + {varepsilon _2} + {varepsilon _3}].
Если подставить вдносні деформации из обобщенного закона Гука, получим
[begin{gathered} {varepsilon _v} = {varepsilon _1} + {varepsilon _2} + {varepsilon _2} = frac{1}{E}left( {{sigma _1} — nu {sigma _2} — nu {sigma _3} + {sigma _2} — nu {sigma _1} — nu {sigma _3} + {sigma _3} — nu {sigma _1} — nu {sigma _2}} right) = hfill \ = frac{1}{E}left( {{sigma _1} + {sigma _2} + {sigma _3} — 2nu cdot left( {{sigma _1} + {sigma _2} + {sigma _3}} right)} right) = frac{{1 — 2nu }}{E}left( {{sigma _1} + {sigma _2} + {sigma _3}} right) hfill \ end{gathered} ]
[{varepsilon _v} = frac{{1 — 2nu }}{E}left( {{sigma _1} + {sigma _2} + {sigma _3}} right)] – об’емкий закон Гука.
Если среднее арифметическое значение главных напряжений ![]() , то объемный закон Гука можно записать так
, то объемный закон Гука можно записать так
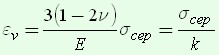 ,
,
где [k = frac{E}{{3left( {1 — 2nu } right)}}] – модуль объемной деформации, а
[{varepsilon _v} = frac{{{sigma _1} + {sigma _2} + {sigma _3}}}{k}].
Потенциальная энергия деформации
При деформации любого тела тратится определенное количество энергии, которая может превращаться в тепловую (при пластическом деформировании), или накапливаться внутри тела в виде внутренней энергии деформации (при упругом деформировании). В последнем случае при разгрузке тела эта накопленная внутренняя энергия выполняет работу.
Определим внутреннюю энергию, которая накапливается в стержне, растянутом силой $F$. Удлинение, которую приобретет стержень, определится по закону Гука
$Delta l = frac{{F cdot l}}{{EA}}$.
Работа, затраченные силой $F$ на перемещении $Delta l$, определяется как $F cdot Delta l$, но это справедливо только в случае, когда сила является неизменной в процессе удлинения стержня. На самом деле, значение силы изменяется от 0 до [F] пропорционально удлинению. Поэтому в случае деформирования тела работа, затраченные на деформирование, а вместе с ней и потенциальная энергия деформации будет определяться как
[U = frac{{F cdot Delta l}}{2} = frac{F}{2} cdot frac{{F cdot l}}{{EA}} = frac{{{F^2} cdot l}}{{2EA}}].
Удельная потенциальная энергия, которая накапливается в единице об’объема материала)
[u = frac{U}{V} = frac{{F cdot Delta l}}{{2 cdot A cdot l}} = frac{1}{2} cdot frac{F}{A} cdot frac{{Delta l}}{l} = frac{1}{2} cdot sigma cdot varepsilon = frac{{sigma cdot varepsilon }}{2} = frac{{{sigma ^2}}}{{2E}}].
В случае действия касательных напряжений аналогично
[u = frac{{tau cdot gamma }}{2} = frac{{{tau ^2}}}{{2G}}].
В случае о’объемного напряженного состояния
[begin{gathered} u = frac{{{sigma _1} cdot {varepsilon _1}}}{2} + frac{{{sigma _2} cdot {varepsilon _2}}}{2} + frac{{{sigma _3} cdot {varepsilon _3}}}{2} = hfill \ = frac{1}{{2E}}left( {{sigma _1} cdot left( {{sigma _1} — nu ({sigma _2} + {sigma _3})} right) + {sigma _2} cdot left( {{sigma _2} — nu ({sigma _1} + {sigma _3})} right) + {sigma _3} cdot left( {{sigma _3} — nu ({sigma _1} + {sigma _2})} right)} right) hfill \ end{gathered} ]
После упрощения имеем
[u = frac{1}{{2E}}left( {sigma _1^2 + sigma _2^2 + sigma _3^2 — 2nu cdot left( {{sigma _1}{sigma _2} + {sigma _2}{sigma _3} + {sigma _1}{sigma _3}} right)} right)].
При этом можно отдельно выделить потенциальную энергию, которая соответствует изменению о’объема тела
![]()
и изменении формы тела
![]() .
.
Зависимости между модулем упругости E и модулем сдвига G
Рассмотрим частный случай плоского напряженного состояния – чистый сдвиг, при котором на некоторых площадках возникают только касательные напряжения [tau ]. Ранее показано, что при чистом сдвиге главными площадками являются площадки, которые находятся под углом 45 в рассматриваемых. Главные напряжения при этом
[begin{gathered} {sigma _1} = tau hfill \ {sigma _2} = 0 hfill \ {sigma _3} = — tau hfill \ end{gathered} ]
Тогда потенциальная энергия деформации
[u = frac{1}{{2E}}left( {tau _{}^2 + 0 + tau _{}^2 — 2nu cdot left( {0 + 0 — {tau ^2}} right)} right) = frac{{2 + 2nu }}{{2E}}{tau ^2} = frac{{1 + nu }}{E}{tau ^2}].
Если рассмотреть ту же самую энергию на площадках, где возникают только касательные напряжения, то
[u = frac{{{tau ^2}}}{{2G}}].
Отсюда [frac{{1 + nu }}{E}{tau ^2} = frac{{{tau ^2}}}{{2G}}], то есть между модулем упругости E, модулем сдвига G и коэффициентом Пуассона $nu$ существует взаимозависимость
[G = frac{E}{{2left( {1 + nu } right)}}]
которая справедлива для всех изотропных материалов (материалов, деформівні свойства которых одинаковы во всех направлениях).
Источник
В машиностроении, строительстве и архитектуре при расчетах прочности и жесткости материалов используется математический аппарат технической механики. Деформация растяжения – одно из ключевых понятий, характеризующее механические процессы, происходящие в материалах при приложении к ним внешних воздействий. Для наглядности изучаются изменения, происходящие в брусе с постоянным сечением, характерные для упругой деформации при приложении внешних усилий.
Закон Гука (английский физик Р. Гук, 1653-1703) для упругой деформации растяжения/сжатия гласит, что нормальное напряжение находится в линейной зависимости (прямо пропорционально) к относительному удлинению/укорочению. Математический аппарат технической механики описывает эту формулу следующим образом:
Коэффициент пропорциональности E (модуль упругости, модуль Юнга) – величина определяющая жесткость материала, единица измерения – паскаль (ПА).
Его значения были установлены эмпирическим путем для большинства конструкционных материалов, необходимую информацию можно почерпнуть в справочниках по машиностроению. Относительная деформация является отношением изменения длины бруса к его изначальным размерам, это безразмерная величина, которая иногда отражается в процентном соотношении.
При растяжении или сжатии у бруса меняется не только длина, но происходят поперечные деформации: при сжатии образуется утолщение, при растяжении толщина сечения становится меньше. Величины этих изменений находятся в линейной зависимости друг от друга, причем установлено, что коэффициент пропорциональности Пуассона (фр. ученый С. Пуассон, 1781-1840) остается всегда неизменным для исследуемого материала.
Внутренние усилия при растяжении и сжатии
При приложении к брусу с постоянным сечением внешних воздействий, действие которых в любом поперечном разрезе направлено параллельно его центральной оси и перпендикулярно сечению, с ним происходит следующий вид деформации: растяжение или сжатие. На основе гипотезы о принципе независимости внешнего воздействия для каждого из поперечных разрезов можно рассчитать внутреннее усилие как векторную сумму всех приложенных внешних воздействий. Растягивающие нагрузки в сопромате принято считать положительными, а сжимающие отрицательными.
Рассмотрев произвольный разрез бруса или стержня, можно сказать что внутренние напряжения равны векторной сумме всех внешних сил, сгруппированных по одной из его сторон. Это верно только с учетом принципа Сен-Венана (фр. инженер А. Сен-Венан, 1797-1886) о смягчении граничных условий, т.к. распределение внутренних усилий по поверхности разреза носит сложный характер с нелинейными зависимостями, но в данном случае значением погрешности можно пренебречь как несущественным.
Применяя гипотезу Бернулли (швейцарский математик, И. Бернулли, 1667-1748) о плоских сечениях, для более наглядного представления процессов распределения сил и напряжений по центральной оси бруса можно построить эпюры. Визуальное представление более информативно и в некоторых случаях позволяет получить необходимые величины без сложных расчетов. Графическое представление отражает наиболее нагруженные участки стержня, инженер может сразу определить проблемные места и ограничиться расчетами только для критических точек.
Все вышесказанное может быть применимо при квазистатической (система может быть описана статически) нагрузке стержня с постоянным диаметром. Потенциальная энергия системы на примере растяжения стержня определяется по формуле:
U=W=FΔl/2=N²l/(2EA)
Потенциальная энергия растяжения U концентрируется в образце и может быть приравнена к выполнению работы W (незначительное выделение тепловой энергии можно отнести к погрешности), которая была произведена силой F для увеличения длины стержня на значение абсолютного удлинения. Преобразуя формулу, получаем, что вычислить значение величины потенциальной энергии растяжения можно, рассчитав отношение квадрата продольной силы N помноженной на длину стержня l и удвоенного произведения модуля Юнга E материала на величину сечения A.
Как видно из формулы, энергия растяжения всегда носит положительное значение, для нее невозможно применить гипотезу о независимости действия сил, т.к. это не векторная величина. Единица измерения – джоуль (Дж). В нижней части формулы стоит произведение EA – это так называемая жесткость сечения, при неизменном модуле Юнга она растет только за счет увеличения площади. Величина отношения жесткости к длине бруса рассматривается как жесткость бруса целиком.
Напряжения при растяжении сжатии
Используя гипотезу Бернулли для продольной упругой деформации стержня, можно определить продольную силу N как равнодействующую всех рассредоточенных по сечению внутренних усилий. Гипотеза Бернулли совместно с гипотезой о ненадавливании волокон позволяет сказать, что σ в произвольной точке разреза будут постоянны, т.к. реакция продольных волокон одинакова на всем поперечном разрезе. Для определения величины нормального напряжения σ используется следующая формула:
Напряжение для упруго деформированного стержня описывается как отношение внутренней силы N к площади сечения A. Считается положительным при растяжении, при сжатии рассматривается как отрицательное.
Абсолютная деформация зависит от жесткости сечения, величины продольной силы и длины бруса. Зависимость можно описать по следующей формуле:
Δl=Nl/EA
Таким образом, методика расчета величины абсолютного изменения длины такова: необходимо просчитать отношение значения продольной силы N умноженной на длину стержня l и жесткости сечения (произведение модуля Юнга E на площадь сечения A).
В реальных расчетах на брус действует достаточно много разнонаправленных сил, для решения таких задач требуется построение эпюр, которые могут наглядно показать какие напряжения действуют на разных участках, чем обусловлена деформация при растяжении и сжатии.
В рамках такой квазистатической (условно статической) системы, как брус или стержень с переменным сечением или отверстием, потенциальная энергия растяжения может быть рассмотрена как сумма энергий однородных участков. При проведении расчетов важно правильно разделить стержень на участки и смоделировать все участвующие в процессе силы и напряжения. Для реальных расчетов построение эпюр – сложная задача, которая требует от инженера хорошего понимания действующих на деталь нагрузок. Например, вал со шкивами разного диаметра требует сначала определения критических точек и разбивки на соответствующие участки, затем построения графиков по ним.
Деформации при растяжении сжатии
При растяжении/сжатии бруса могут возникать 2 вида деформации. Первый – упругая, второй – пластическая. Для упругой деформации характерно восстановление первоначальных параметров после прекращения воздействия. В случае пластической стадии деформации материала он утрачивает и не восстанавливает форму и размеры. Величина воздействия для перехода одного вида в другой называется пределом текучести.
Для расчета перемещения при растяжении бруса или стержня следует использовать метод разделения на участки, в рамках которых осуществляется приложение внешних воздействий. В точках воздействия силы следует вычислить величину изменения длины, используя формулу: Δl=Nl/EA. Как видно она зависит от жесткости сечения, длины бруса или стержня и величины действующей продольной силы. Итоговым перемещением для бруса целиком будет сумма всех частичных перемещений, рассчитанных для точек приложения силы.
Поперечные деформации бруса (становится более толстым при сжатии и тонким при растяжении) также характеризуются абсолютной и относительной величиной деформации. Первая – разность между размером сечения после и до приложения внешних воздействий, вторая – отношение абсолютной деформации к его исходному размеру. Коэффициент Пуассона, отражающий линейную зависимость продольной и поперечной деформаций, определяет упругие качества материалов и считается неизменным для растяжения и сжатия. Продольные наиболее наглядно отражают процессы, происходящие в брусе или стержне при внешнем воздействии. Зная величину любой из них (продольной или поперечной) и используя коэффициент Пуассона, можно рассчитать значение неизвестной.
Для определения величины деформации пружины при растяжении можно применить закон Гука для пружин:
F=kx
В данном случае х – увеличение длины пружины, k – коэффициент жесткости (единица измерения Н/м), F – сила упругости, направленная в противоположную от смещения сторону. Величина абсолютной деформации будет равна отношению силы упругости к коэффициенту жесткости. Коэффициент жесткости определяет упругие свойства материала, используемого для изготовления, может быть использован для выбора материала изготовления в условиях решения конкретной задачи.
Расчеты на прочность и жесткость
Прочность характеризует способность конструкционного материала сопротивляться внешним воздействиям без разрушений и остаточных изменений. Жесткость находится в линейной зависимости от модуля Юнга и размера сечения. Чем больше площадь, модуль упругости не меняется, тем больше жесткость. В общем случае жесткость подразумевает способность деформироваться без значительных изменений. Коэффициент запаса прочности – безразмерная величина, равная отношению предельного напряжения к допустимому. Запас прочности характеризует штатный режим работы конструкции даже с учетом случайных и не предусмотренных нагрузок. Наименьшим запасом прочности обладают пластические (1.2-2.5) и хрупкие (2-5) материалы.
Применение в расчетах этих коэффициентов позволяет, например, рассчитать опасную толщину для стержня, при которой может возникнуть максимальное нормальное напряжение. Используя коэффициент прочности и возможное предельное напряжение возможно произвести расчет необходимого диаметра вала, который гарантированно обеспечит упругую деформацию и не приведет к пластической. Для инженеров-экономистов важны расчеты наименьших безопасных размеров деталей конструкции по заданным нагрузкам.
Большинство практических расчетов на прочность и жесткость производятся для получения минимальных значений геометрических размеров конструкционных элементов и деталей машин в условиях известных внешних воздействий и необходимого и достаточного запаса прочности. Может решаться обратная задача получения значений предельных нагрузок при условии сохранения геометрических размеров и для конкретного материала.
Сложные конструкции могут быть разделены на элементарные части, для которых будут производиться расчеты, затем полученные результаты интерпретируются в рамках всей системы, для этого удобно строить эпюры распределения внешних воздействий и внутренних напряжений статически определенной системы.
С помощью известной жесткости материала делают расчеты максимально возможной длины балки или стержня (вала) при условии неизменности его сечения. Для ступенчатых валов необходимо строить эпюры воздействия внешних сил и возникающих в точках их приложения внутренних напряжений в критических точках. От правильно построенной теоретической модели будет зависеть насколько эффективно и долго прослужит вал для станка, не разрушится ли он от динамических крутящих моментов. На этапе проектирования можно выявить потенциальные слабые точки и рассчитать необходимые параметры для заданного предела прочности.
С расчетами на прочность связаны такие понятия, как срез и смятие. Срез проявляется в виде разрушения детали соединения в условиях возникновения в ее поперечном сечении перпендикулярной к нему и достаточной силы.
При расчетах соединений используют пределы текучести используемых материалов и коэффициенты запаса прочности, вычисляют максимально возможные напряжения.
Исследования на прочность обычно подразумевают решение нескольких задач: в условиях проведения поверочного расчета на проверку прочности при известных усилиях и площади сечения оценивают фактический коэффициент запаса прочности; подбор оптимального диаметра при заданных нагрузках и допустимом напряжении; вычисляют грузоподъемность или несущую способность с помощью определения внутреннего усилия при известной площади сечения и напряжении.
Прочностные расчеты при разных видах воздействий в рамках условно статических систем сложны, требуют учета многих, иногда не очевидных, факторов, их практическая ценность заключается в вычислении допустимых размеров конструкционных материалов для заданных параметров запаса прочности.
Источник
