Напряженное состояние при растяжении сжатии кручении
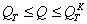
Рассмотрим более детально особенности напряженного состояния, возникающего в однородном растянутом стержне.
Рис. 1.18
Определим сначала напряжения в некоторой наклонной площадке, составляющей угол а с плоскостью нормального сечения (рис. 1.18). Полное напряжение на этой площадке, согласно условию однородности напряженного состояния для всех точек площадки, будет одним и тем же. Равнодействующая же внутренних сил в сечении должна быть направлена по оси стержня и равна растягивающей силе т. е.
где — площадь косого сечения, . Таким образом, полное напряжение на наклонной площадке
Раскладывая это напряжение по нормали и по касательной к наклонной площадке (рис. 1.18, б), находим
или
Как видим, для одной и той же точки растянутого стержня значения возникающих в сечении напряжений оказываются различными в зависимости от ориентации секущей площадки. Поэтому, в частности, неточным было бы утверждение, что при растяжении возникают только нормальные напряжения. Это верно только для площадок, нормальных к оси стержня.
Если положить то из выражений (1.10) и (1.11) мы получим напряжения в поперечном сечении стержня, т. е.
При т. е. в продольных сечениях, ста Это значит, что продольные слои растянутого стержня не имеют между собой силового взаимодействия по боковым поверхностям. В этом смысле растяжение стержня можно уподобить растяжению пучка не связанных между собой параллельных нитей.
Касательное напряжение та, обращаясь в нуль в продольных и поперечных сечениях, имеет наибольшее значение на площадках, наклоненных под углом 45° к оси растянутого стержня:
Если из растянутой полосы мы выделим прямоугольник (рис. 1.19, а), то на его гранях АВ и следует приложить напряжения , определяемые выражениями (1.10) и (1.11).
Рис. 1.19
На рис. 1.19, б эти напряжения отмечены сверху штрихом. На гранях и напряжения вычисляют также по формулам (1.10), (1.11), в которых только угол а заменяют углом а Эти напряжения отмечены двумя штрихами. Таким образом, то напряженное состояние, которое показано на рис. 1.19, б, представляет собой обыкновенное растяжение, но изображенное в непривычном для нас ракурсе.
Существенно отметить, что переход от произвольной площадки а к площадке не сказывается на абсолютной величине касательного напряжения та. Действительно,
Следовательно, на двух взаимно перпендикулярных площадках (если отвлечься пока от знаков) касательные напряжения должны быть равными. Это условие является общей особенностью любого напряженного состояния и носит название закона парности касательных напряжений.
Этому закону можно дать наглядное толкование. Если рассмотреть произвольно взятый элемент (см. рис. 1.19, а), то легко заметить, что, независимо от значений нормальных напряжений о и касательные напряжения должны иметь такое значение и такое направление, чтобы моменты их пар взаимно уравновешивались (см. рис. 1.19, б). Для произвольно взятого элемента, имеющего толщину , очевидно, что
Таким образом,
При этом, как видно на рис. 1.19, б, векторы касательных напряжений в двух взаимно перпендикулярных площадках направлены либо оба к общему ребру (ребра А и С), либо от общего ребра
Закон парности касательных напряжений в самом общем виде сложного напряженного состояния будет рассмотрен еще раз в гл. 7.
Теперь обратимся к анализу деформированного состояния растянутого стержня.
Наблюдения показывают, что удлинение стержня в осевом направлении сопровождается уменьшением его поперечных размеров (рис. 1.20). Таким образом, при растяжении возникает не только продольная, но и поперечная деформация стержня:
Рис. 1.20
Экспериментально установлено, что в пределах применимости закона Гука поперечная деформация пропорциональна продольной:
где — безразмерный коэффициент пропорциональности, называемый коэффициентом Пуассона. Коэффициент характеризует свойства материала. Определяют его экспериментальным путем. Для всех металлов числовые значения лежат в пределах . В дальнейшем, в гл. 7, будет показано, что для изотропного материала значение вообще не может превышать 0,5.
Вернемся к рис. 1.19, а. Полоса удлиняется в продольном направлении и сужается в поперечном. Стороны прямоугольника начерченного на поверхности полосы, изменят свою длину, а сам прямоугольник перекосится и превратится в параллелограмм. Углы А и С уменьшатся, а В и — увеличатся. Это изменение прямого угла для заданной ориентации сторон, как нам уже известно, называется угловой деформацией или углом сдвига. Чтобы найти его, мы определим сначала углы, на которые повернутся отрезки АВ и Разность этих углов и даст нам искомый угол сдвига.
Начнем с отрезка АВ (рис. 1.21). Построим на нем, как на диагонали, вспомогательный прямоугольник стороны которого и ориентированы по продольной оси стержня. Вследствие продольного удлинения точка В переместится вправо и отрезок АВ повернется на угол
Рис. 1.21
В результате поперечного сужения отрезок АВ получит дополнительный угол поворота
Сумма этих углов дает нам искомый угол поворота отрезка АВ:
или
Изменяя угол а на 90°, найдем положение отрезка АВ:
Угловая деформация (угол сдвига) определяется разностью углов поворота отрезков, и, следовательно,
Сопоставляя это выражение с выражением (1.11), выведенным для напряжения та, замечаем, что угол сдвига между плоскостями АВ и АС независимо от а пропорционален касательному
напряжению, т.е.
Это соотношение в случае изотропного материала является единым для всех типов напряженных состояний и носит название закона Гука для сдвига. Опуская индекс а, напишем последнее выражение в виде
где величина называется модулем сдвига, или модулем упругости второго рода:
Модуль измеряется в тех же единицах, что и модуль Е.
Таким образом, если закон Гука для растяжения постулируется при помощи соотношений (1.4) и (1.12), то для сдвига он вытекает из них как следствие.
Источник
Напряженное состояние сдвиге
Кроме деформации растяжения или сжатия материал нагруженного элемента конструкции может испытывать деформацию сдвига.
Рассмотрим частный случай плоского напряженного состояния, для которого отличные от нуля главные напряжения равны по модулю и противоположны по знаку (рис. 2.6.1, а).
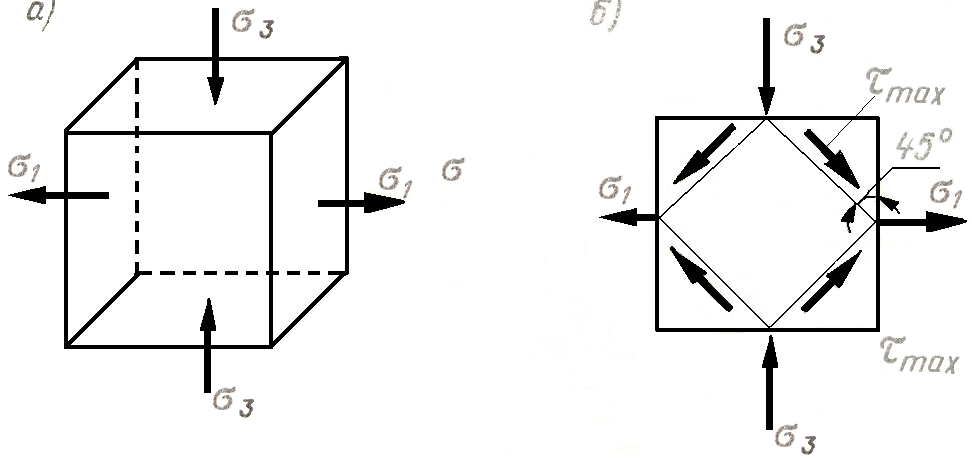
Рисунок 2.6.1
Такое напряженное состояние носит название чистого сдвига (происхождение этого названия разъяснено несколько ниже).
На рис. 2.6.1,б показана проекция элемента на плоскость, совпадающую с нулевой главной площадкой (отмечена на рис.2.6.1,а точками).
Максимальное для исследуемой серии площадок касательное напряжение при α = 45°, max τα= σ1. Это напряжение максимально для данной точки тела, а не только для исследуемой серии площадок, так как эти площадки параллельны вектору σ2.
Итак, при чистом сдвиге:
τ13=τmax=σ1= -σ3 (2.6.3)
На площадках действия максимальных касательных напряжений нормальные напряжения отсутствуют; эти площадки показаны на рис. 2.6.1,б.
Чистый сдвиг — единственный случай плоского напряженного состояния, когда через точку можно проверти две взаимно перпендикулярные площадки, на которых касательные напряжения максимальны, а нормальные напряжения отсутствуют.
Итак, наряду с определением
чистый сдвиг — это частный случай плоского напряженного состояния, при котором не равные нулю главные напряжения равны по значению н противоположны по знаку,
возможно и другое определение, вытекающее из проведенного исследования:
чистым сдвигом называют такое плоское напряженное состояние, при котором в окрестности данной точки можно выделить элемент таким образом, чтобы на четырех его гранях были только равные между собой касательные напряжения.
Это последнее определение можно рассматривать как объяснение названия, принятого для данного напряженного состояния.
Деформации сдвига
Рассмотрим теперь вопрос о деформации сдвига. Изобразим элемент, выделенный площадками, на которых возникают только касательные напряжения, в проекции на плоскость, параллельную свободной от напряжений грани (рис. 2.6.2), Учитывая, что нас интересуют деформации элемента, а не его перемещения как твёрдого тела, будем считать одну из граней неподвижной.
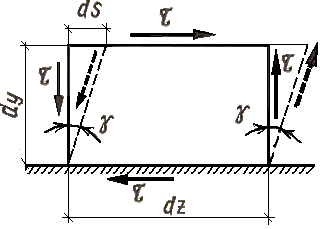
Рисунок 2.6.2
В результате деформации элемент примет форму показанную на рис. 2.6.2 штриховыми линиями. Мерой деформации сдвига служит изменение первоначального прямого угла между гранями элемента, называемое углом сдвига и обозначаемое γ. Угол сдвига выражается в радианах.
В известных пределах, зависящих от свойств материала, между углом сдвига и соответствующим касательным напряжением существует прямая пропорциональность — закон Гука при сдвиге. Математическая запись этого закона имеет вид:
τ=Gγ (2.6.4)
Здесь G — упругая постоянная материала, характеризующая его жесткость при деформации сдвига и называемая модулем сдвига или модулем упругости 2-го рода. Очевидно, размерность модуля сдвига та же, что и напряжения.
Можно доказать, что для изотропного тела между тремя упругими постоянными — модулем продольной упругости Е коэффициентом Пуассона ν и модулем сдвига G — существует следующая зависимость:
(2.6.5)
Как известно, значение коэффициента Пуассона лежит в пределах 0 < ν < 0,5 (см. лекцию 2.4). Следовательно, модуль сдвига составляет 0,33…0,5 от модуля продольной упругости. Для многих металлов и сплавов, в частности для стали, G = 0,4Е; в среднем для стали G = 8,0* 104 МПа.
.
Напряженное состояние при кручении. Деформации кручения.
Общая деформация кручен стержня с круглым сечением изображена на рис. 2.6.3. Эта деформация характерна тем, что по сечения поворачиваются вокруг оси стержня на φ=φ(z), называемые углами закручивания, а в поперечных сечениях возникают касательные напряжения τ приводящие к крутящему моменту Мг
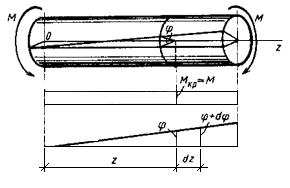
Рисунок 2.6.3
Напомним правило знаков для момента Мг: при взгляде на торцевое сечения элемента стержня со стороны его внешней нормали положительный момент направлен походу часовой стрелки. Угол поворота φ>0, если при взгляде на сечение в положительном направлении оси z видим поворот против часовой стрелки, см. рис.2.6.4:
Рисунок 2.6.4
Вывод формулы для касательных напряжений. Первое допущение состоит в том, что будем считать справедливой гипотезу плоских сечений, т. е. примем, что поперечные сечения при кручении, поворачиваясь вокруг оси z, остаются плоскими. Заметим, что для сечения не круглой формы это положение в общем случае не справедливо сечения при кручении искривляются, что существенно усложняет задачу см.рис 2.6.5:
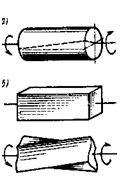
Рисунок 2.6.5
Второе допущение утверждает, что все радиусы данного сечения остаются прямыми и поворачиваются на один и тот же угол φ, т. е. каждое поперечное сечение поворачиваясь вокруг оси z как жесткий тонкий диск.
Согласно этим допущениям кручение представляет деформацию сдвига материала, заключенного между соседними поперечными сечениями, вызванную относительным поворотом этих сечений вокруг оси z.
С использованием указанных допусков на рис. 5 изображена деформация элемента стержня длинной dz выделенного из закручиваемого стержня (см. рис. 2.6.6) при произвольном значении z.
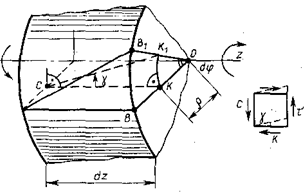
Рисунок 2.6.6
Произведя необходимые вычисления получим формулу для касательных напряжений τ:
(2.6.6)
, где Мг – крутящий момент;
ρ – радиус окружности (см. рис. 2.6.6);
Jρ – полярный момент инерции сечения, для круглого стержня:
Подчеркнем, что по закону о парности касательных напряжений формула (2.6.6) определяет касательное напряжение в плоскости поперечного сечения и одновременно возникающее напряжение в перпендикулярной плоскости диаметрального продольного сечения вала. На рис. 2.6.7 показано распределение касательных напряжений вдоль радиуса в двух указанных сечениях. Каждый прямоугольный элемент материала, показанный на рис. 2.6.7, испытывает напряженное состояние чистого сдвига
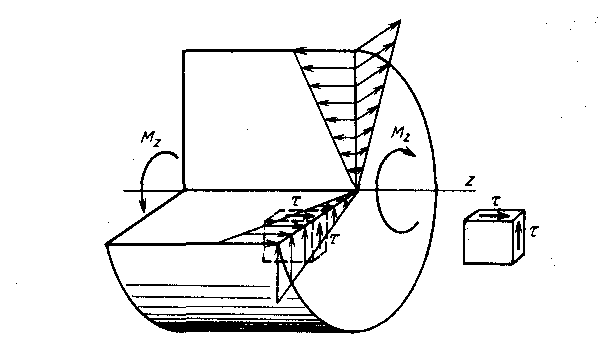
Рисунок 2.6.7
Источник
В начале курса при первом знакомстве с понятием «напряжение» было подчеркнуто, что нельзя говорить о напряжении в данной точке тела, не указывая положения площадки, на которой оно возникает. Действительно, через точку можно провести бесчисленное множество различно ориентированных площадок, и, конечно, в общем случае нет никаких оснований предполагать, что возникающие на них напряжения одинаковы.
Совокупность нормальных и касательных напряжений, возникающих на всем бесчисленном множестве площадок, которые можно провести через данную точку, характеризует напряженное состояние в этой точке.
Исследовать напряженное состояние в данной точке — это значит получить зависимости, позволяющие определить напряжения, возникающие в любой проведенной через нее площадке. Для решения этой задачи надо знать напряжения по любым трем взаимно перпендикулярным площадкам, проведенным через исследуемую точку (доказательства этого положения не приводим). Эти площадки и возникающие на них напряжения (они, повторяем, должны быть известны) называют исходными.
При исследовании напряженного состояния в различных точках прямого бруса в любом случае его нагружения исходными являются напряжения, возникающие на площадках, соответствующих поперечному и двум продольным сечениям, проходящим через рассматриваемую точку. При растяжении (сжатии) прямого бруса в поперечных сечениях возникают только нормальные напряжения, определяемые по формуле:
σz=N/A (2.5.1)
Индекс z показывает, что это напряжение возникает на площадке, нормаль к которой параллельна оси z . В продольных сечениях нет ни нормальных, ни касательных напряжений.
Отсутствие нормальных напряжений в продольных сечениях является следствием того, что при растяжении (сжатии) нет взаимного надавливания волокон бруса. В отсутствии касательных напряжений легко убедиться, рассекая брус продольной плоскостью и рассматривая условие равновесия одной из его отсеченных частей,
Для исследования напряженного состояния мысленно вырежем вокруг произвольной точки бруса бесконечно малый параллелепипед (рис. 2.5.3, а). В дальнейшем такие элементарные параллелепипеды будем называть элементами или частицами.
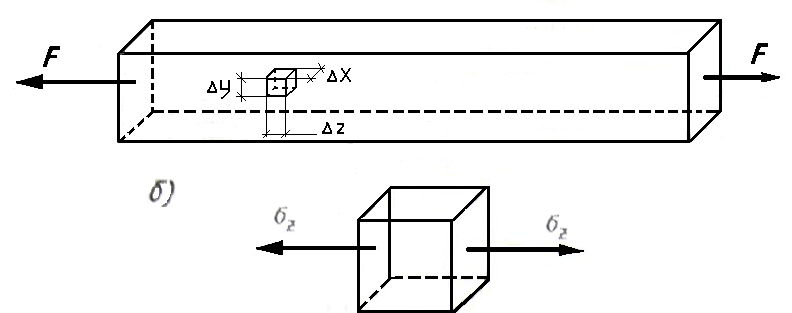
Рисунок 2.5.3
В рассматриваемом случае совершенно безразлично, где именно вырезать эту частицу, так как напряженное состояние всех точек бруса одинаково — однородное напряженное состояние.
Для того чтобы выделенный элемент находился в равновесии, следует приложить к его граням внутренние силы, заменяющие действие отброшенных частей тела (бруса) на оставленную. Обращаем внимание, что здесь мы поступаем в полном соответствии с требованиями метода сечений, но если ранее при определении продольных сил было достаточно рассечь брус плоскостью, совпадающей с интересующим нас поперечным сечением, то новая задача — исследование напряженного состояния — потребовала иного применения этого метода: элемент вырезан шестью сечениями.
Выделенный элемент (модель напряженной точки) изображен отдельно на рис. 2.5.3,6. На его гранях, совпадающих с плоскостями поперечного сечения бруса, возникают нормальные напряжения, остальные четыре грани от напряжений свободны.
Источник
Напряженное
состояние при растяжении стержня
является одноосным (рис. 9, а). Поскольку
на поперечных и продольных площадках
касательные напряжения не возникают,
то эти площадки являются главными.
Причем в случае растяжения
,
а в случае сжатия
.
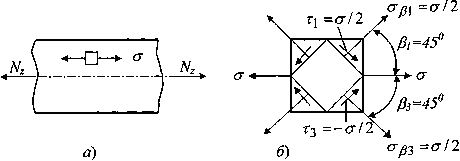Рис.9.
Напряженное состояние: а
) исходный элемент, б
) компоненты напряжений
Напряжения
на площадках, наклоненных к оси стержня
под углом
,
определяются по формулам для упрощенного
плоского напряженного состояния:
Площадки
с экстремальными касательными напряжениями
(рис.
9, б),
как известно, наклонены по отношению к
исходным под углами
(следует
и из формулы для
)
и равны
.
Именно
с действием экстремальных
связывается
появление на боковой поверхности образца
из малоуглеродистой стали, испытываемого
на растяжение, линий скольжения,
ориентированных под углом
к
оси образца. На площадках с экстремальными
действуют
и нормальные напряжения, равные
.
Лекция
№ 13.
Расчет статически неопределимых систем
по допускаемым нагрузкам.
Применение к статически определимым системам.
В
предыдущем изложении методов расчета
мы исходили из основного условия
прочности
.
Это неравенство требует выбора размеров
конструкции с таким расчетом, чтобы
наибольшее напряжение в самом опасном
месте не превосходило допускаемого.
Но
можно стать на другую точку зрения.
Можно задать условие, чтобы действительная
нагрузка на всю конструкцию не превосходила
некоторой допускаемой величины. Условие
это можно выразить таким неравенством:
За
допускаемую нагрузку надо выбрать
некоторую
часть
той нагрузки, при которой конструкция
перестанет функционировать правильно,
перестанет выполнять свой назначение.
Такая нагрузка обычно называется
предельной,
иногда—разрушающей
в широком смысле слова (под разрушением
конструкции подразумевают прекращение
ее нормальной работы).
В
качестве примера возьмем систему из
двух стальных стержней АВ
и АС,
(рис.1), нагруженных силой P.
Рис.1.
Расчетная схема статически определимой
стержневой системы
Рассчитывая
эту систему обычным путем, найдем усилия
N1
= N2
no формуле:
(из
равновесия узла А). Отсюда площадь
каждого из стержней равна:
По
способу допускаемых нагрузок имеем:
Введя
в качестве коэффициента запаса для
конструкции в целом ту же величину k,
которая была принята в качестве
коэффициента запаса для напряжений, мы
получим, что величина
Предельной,
опасной величиной Pпр
будет та, при которой напряжения в
стержнях дойдут до предела текучести:
Таким
образом, допускаемая величина Р
равна:
Условие
прочности принимает вид
а
учитывая, что
,
получаем:
Отсюда:
Таким
образом, расчет по допускаемым нагрузкам
привел в данном случае к тем же результатам,
что и расчет по допускаемым напряжениям.
Это всегда имеет место для статически
определимых конструкций при равномерном
распределении напряжений, когда материал
по всему сечению используется полностью.
Расчет статически неопределимых систем по способу допускаемых нагрузок.
Совсем
другие результаты мы получим, если будем
применять способ допускаемых нагрузок
к статически неопределимым системам,
стержни которых изготовлены из материала,
обладающего способностью к большим
пластическим деформациям, например из
малоуглеродистой стали.
В
качестве примера рассмотрим систему
из трех стержней, нагруженных силой Q
(рис. 2). Пусть все стержни сделаны из
малоуглеродистой стали с пределом
текучести
.
Длины крайних стержней, как и выше,
обозначим
;
длину среднего
.
Допускаемое напряжение
Рис.2.
Расчетная схема однократно статически
неопределимой стержневой системы.
Как
и раньше, при расчете этой статически
неопределимой системы зададимся
отношением площадей стержней; примем,
что все три стержня будут иметь одинаковую
площадь F.
Получим:
Используя
закон Гука, получим:
Следовательно:
Так
как
,
средний стержень напряжен больше, чем
крайние; поэтому подбор площади сечения
F надо произвести по формуле:
Ту
же величину площади надо дать и боковым
стержням; в них получается некоторый
дополнительный запас.
Применим
способ допускаемых нагрузок; условием
прочности будет:
Что
в данном случае следует понимать под
предельной нагрузкой конструкции? Так
как конструкция выполнена из материала,
имеющего площадку текучести, то, по
аналогии с простым растяжением стержня
из такого материала, за предельную
нагрузку следует взять груз, соответствующий
достижению состояния текучести для
всей конструкции в целом.
Назовем эту нагрузку
.
Пока сила Q
не достигла этого значения, для дальнейшей
деформации (опускания точки A)
требуется возрастание нагрузки. Когда
же Q
сделается
равным
,
дальнейший рост деформаций будет
происходить уже без увеличения нагрузки,
— конструкция выйдет из строя.
Для
определения величины
рассмотрим
постепенный ход деформации нашей
стержневой системы. Так как средний
стержень напряжен сильнее крайних, то
в нем раньше, чем в других, напряжение
дойдет до предела текучести. Нагрузку,
соответствующую этому моменту, обозначим
QТ;
она будет равна:
где
—
усилие в среднем стержне, соответствующее
его пределу текучести.
Напряжения
в крайних стержнях, имеющих ту же площадь,
в этот момент еще не дойдут до предела
текучести, и эти стержни будут упруго
сопротивляться дальнейшей деформации.
Для того чтобы эта деформация происходила,
необходимо дальнейшее увеличение
нагрузки до тех пор, пока в крайних
стержнях напряжения тоже не дойдут до
предела текучести. Лишь тогда будет
достигнута предельная грузоподъемность
конструкции
.
Так
как при нагрузке QТ
напряжения в среднем стержне дойдут
уже до предела текучести
,
то при дальнейшем возрастании груза
они, а стало быть и усилие N3,
останутся без
увеличения.
Наша статически неопределимая система
превратится в статически определимую,
состоящую из двух стержней АВ
и АС
и нагруженную в точке А
силой Q,
направленной вниз, и известным
усилием
,
равным
(Рис.3).
Рис.3.
Эквивалентная статически определимая
система
Такая
схема работы нашей конструкции будет
иметь место, пока
Для
иллюстрации хода деформации рассматриваемой
конструкции изобразим графически
зависимость между силой Q
и перемещением f
точки А
(Рис. 4). Пока
опускание
точки А
равно удлинению среднего стержня и
определяется формулой
Рис.4.
Динамика деформации в зависимости от
нагрузочной способности системы
Как
только Q
будет заключаться в промежутке
перемещение
точки А
должно быть вычислено, как опускание
этого узла в системе двух стержней АС
и АВ,
нагруженных в точке А
силой
.
Так как:
и,
в свою очередь:
Отсюда
Для
f12
(на втором участке) получаем уравнение
прямой, но уже не проходящей через начало
координат. После достижения нагрузкой
Q
значения
напряжения
в крайних стержнях достигнут предела
текучести, и система будет деформироваться
без увеличения нагрузки. График
перемещения идет теперь параллельно
оси абсцисс.
Для
определения предельной грузоподъемности
всей системы
мы
должны для системы двух стержней,
нагруженных силой
,
найти то значение Q,
при котором напряжения и в крайних
стержнях дойдут до предела текучести.
Такая задача решена в предыдущем
параграфе; подставляя в выражение (а)
§ 26 вместо Р
величину
,
получаем:
Отсюда
Допускаемая
нагрузка будет равна
а
учитывая, что
,
получаем
Окончательно:
и
Эта
величина меньше, чем полученная обычным
методом расчета, т. е.
При
(сталь)
получаем: по обычному способу
по
способу допускаемых нагрузок:
Таким
образом, метод расчета по допускаемым
нагрузкам позволяет спроектировать
статически неопределимую систему из
материала, обладающего площадкой
текучести, экономичнее,
чем при расчете по допускаемым,
напряжениям. Это понятно: при способе
расчета по допускаемым напряжениям мы
считали за предельную нагрузку нашей
конструкции величину QТ,
при которой до предела текучести доходил
лишь материал среднего стержня, крайние
же были недонапряжены. При методе расчета
по допускаемым нагрузкам предельная
грузоподъемность определяется величиной
.
При нагрузке
полностью
используется материал всех трех стержней.
Таким
образом, новый метод расчета позволяет
реализовать скрытые при старом способе
запасы прочности в статически неопределимых
системах, добиться повышения их расчетной
грузоподъемности и действительной
равнопрочности
всех частей конструкции. Не представит
никаких затруднений распространить
этот метод на случай, когда соотношение
площадей среднего и крайних стержней
не будет равно единице.
Изложенные
выше теоретические соображения
проверялись неоднократно на опыте,
причем всегда наблюдалась достаточно
близкая сходимость величин предельной
нагрузки — вычисленной и определенной
при эксперименте. Это дает уверенность
в правильности теоретических предпосылок
метода допускаемых нагрузок.
Лекция
№ 14.
Учет собственного веса при растяжении
и сжатии.
Соседние файлы в предмете Сопротивление материалов
- #
- #
02.05.201422.02 Кб70Курсовая работа — Расчет на прочность.xls
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник