Напряженное состояние одноосное растяжение
В начале курса при первом знакомстве с понятием «напряжение» было подчеркнуто, что нельзя говорить о напряжении в данной точке тела, не указывая положения площадки, на которой оно возникает. Действительно, через точку можно провести бесчисленное множество различно ориентированных площадок, и, конечно, в общем случае нет никаких оснований предполагать, что возникающие на них напряжения одинаковы.
Совокупность нормальных и касательных напряжений, возникающих на всем бесчисленном множестве площадок, которые можно провести через данную точку, характеризует напряженное состояние в этой точке.
Исследовать напряженное состояние в данной точке — это значит получить зависимости, позволяющие определить напряжения, возникающие в любой проведенной через нее площадке. Для решения этой задачи надо знать напряжения по любым трем взаимно перпендикулярным площадкам, проведенным через исследуемую точку (доказательства этого положения не приводим). Эти площадки и возникающие на них напряжения (они, повторяем, должны быть известны) называют исходными.
При исследовании напряженного состояния в различных точках прямого бруса в любом случае его нагружения исходными являются напряжения, возникающие на площадках, соответствующих поперечному и двум продольным сечениям, проходящим через рассматриваемую точку. При растяжении (сжатии) прямого бруса в поперечных сечениях возникают только нормальные напряжения, определяемые по формуле:
σz=N/A (2.5.1)
Индекс z показывает, что это напряжение возникает на площадке, нормаль к которой параллельна оси z . В продольных сечениях нет ни нормальных, ни касательных напряжений.
Отсутствие нормальных напряжений в продольных сечениях является следствием того, что при растяжении (сжатии) нет взаимного надавливания волокон бруса. В отсутствии касательных напряжений легко убедиться, рассекая брус продольной плоскостью и рассматривая условие равновесия одной из его отсеченных частей,
Для исследования напряженного состояния мысленно вырежем вокруг произвольной точки бруса бесконечно малый параллелепипед (рис. 2.5.3, а). В дальнейшем такие элементарные параллелепипеды будем называть элементами или частицами.
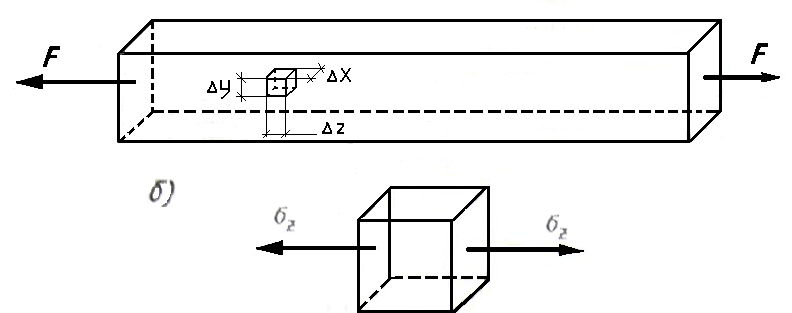
Рисунок 2.5.3
В рассматриваемом случае совершенно безразлично, где именно вырезать эту частицу, так как напряженное состояние всех точек бруса одинаково — однородное напряженное состояние.
Для того чтобы выделенный элемент находился в равновесии, следует приложить к его граням внутренние силы, заменяющие действие отброшенных частей тела (бруса) на оставленную. Обращаем внимание, что здесь мы поступаем в полном соответствии с требованиями метода сечений, но если ранее при определении продольных сил было достаточно рассечь брус плоскостью, совпадающей с интересующим нас поперечным сечением, то новая задача — исследование напряженного состояния — потребовала иного применения этого метода: элемент вырезан шестью сечениями.
Выделенный элемент (модель напряженной точки) изображен отдельно на рис. 2.5.3,6. На его гранях, совпадающих с плоскостями поперечного сечения бруса, возникают нормальные напряжения, остальные четыре грани от напряжений свободны.
Источник
Рассмотрим более детально особенности напряженного состояния, возникающего в однородном растянутом стержне.
Рис. 1.18
Определим сначала напряжения в некоторой наклонной площадке, составляющей угол а с плоскостью нормального сечения (рис. 1.18). Полное напряжение на этой площадке, согласно условию однородности напряженного состояния для всех точек площадки, будет одним и тем же. Равнодействующая же внутренних сил в сечении должна быть направлена по оси стержня и равна растягивающей силе т. е.
где — площадь косого сечения, . Таким образом, полное напряжение на наклонной площадке
Раскладывая это напряжение по нормали и по касательной к наклонной площадке (рис. 1.18, б), находим
или
Как видим, для одной и той же точки растянутого стержня значения возникающих в сечении напряжений оказываются различными в зависимости от ориентации секущей площадки. Поэтому, в частности, неточным было бы утверждение, что при растяжении возникают только нормальные напряжения. Это верно только для площадок, нормальных к оси стержня.
Если положить то из выражений (1.10) и (1.11) мы получим напряжения в поперечном сечении стержня, т. е.
При т. е. в продольных сечениях, ста Это значит, что продольные слои растянутого стержня не имеют между собой силового взаимодействия по боковым поверхностям. В этом смысле растяжение стержня можно уподобить растяжению пучка не связанных между собой параллельных нитей.
Касательное напряжение та, обращаясь в нуль в продольных и поперечных сечениях, имеет наибольшее значение на площадках, наклоненных под углом 45° к оси растянутого стержня:
Если из растянутой полосы мы выделим прямоугольник (рис. 1.19, а), то на его гранях АВ и следует приложить напряжения , определяемые выражениями (1.10) и (1.11).
Рис. 1.19
На рис. 1.19, б эти напряжения отмечены сверху штрихом. На гранях и напряжения вычисляют также по формулам (1.10), (1.11), в которых только угол а заменяют углом а Эти напряжения отмечены двумя штрихами. Таким образом, то напряженное состояние, которое показано на рис. 1.19, б, представляет собой обыкновенное растяжение, но изображенное в непривычном для нас ракурсе.
Существенно отметить, что переход от произвольной площадки а к площадке не сказывается на абсолютной величине касательного напряжения та. Действительно,
Следовательно, на двух взаимно перпендикулярных площадках (если отвлечься пока от знаков) касательные напряжения должны быть равными. Это условие является общей особенностью любого напряженного состояния и носит название закона парности касательных напряжений.
Этому закону можно дать наглядное толкование. Если рассмотреть произвольно взятый элемент (см. рис. 1.19, а), то легко заметить, что, независимо от значений нормальных напряжений о и касательные напряжения должны иметь такое значение и такое направление, чтобы моменты их пар взаимно уравновешивались (см. рис. 1.19, б). Для произвольно взятого элемента, имеющего толщину , очевидно, что
Таким образом,
При этом, как видно на рис. 1.19, б, векторы касательных напряжений в двух взаимно перпендикулярных площадках направлены либо оба к общему ребру (ребра А и С), либо от общего ребра
Закон парности касательных напряжений в самом общем виде сложного напряженного состояния будет рассмотрен еще раз в гл. 7.
Теперь обратимся к анализу деформированного состояния растянутого стержня.
Наблюдения показывают, что удлинение стержня в осевом направлении сопровождается уменьшением его поперечных размеров (рис. 1.20). Таким образом, при растяжении возникает не только продольная, но и поперечная деформация стержня:
Рис. 1.20
Экспериментально установлено, что в пределах применимости закона Гука поперечная деформация пропорциональна продольной:
где — безразмерный коэффициент пропорциональности, называемый коэффициентом Пуассона. Коэффициент характеризует свойства материала. Определяют его экспериментальным путем. Для всех металлов числовые значения лежат в пределах . В дальнейшем, в гл. 7, будет показано, что для изотропного материала значение вообще не может превышать 0,5.
Вернемся к рис. 1.19, а. Полоса удлиняется в продольном направлении и сужается в поперечном. Стороны прямоугольника начерченного на поверхности полосы, изменят свою длину, а сам прямоугольник перекосится и превратится в параллелограмм. Углы А и С уменьшатся, а В и — увеличатся. Это изменение прямого угла для заданной ориентации сторон, как нам уже известно, называется угловой деформацией или углом сдвига. Чтобы найти его, мы определим сначала углы, на которые повернутся отрезки АВ и Разность этих углов и даст нам искомый угол сдвига.
Начнем с отрезка АВ (рис. 1.21). Построим на нем, как на диагонали, вспомогательный прямоугольник стороны которого и ориентированы по продольной оси стержня. Вследствие продольного удлинения точка В переместится вправо и отрезок АВ повернется на угол
Рис. 1.21
В результате поперечного сужения отрезок АВ получит дополнительный угол поворота
Сумма этих углов дает нам искомый угол поворота отрезка АВ:
или
Изменяя угол а на 90°, найдем положение отрезка АВ:
Угловая деформация (угол сдвига) определяется разностью углов поворота отрезков, и, следовательно,
Сопоставляя это выражение с выражением (1.11), выведенным для напряжения та, замечаем, что угол сдвига между плоскостями АВ и АС независимо от а пропорционален касательному
напряжению, т.е.
Это соотношение в случае изотропного материала является единым для всех типов напряженных состояний и носит название закона Гука для сдвига. Опуская индекс а, напишем последнее выражение в виде
где величина называется модулем сдвига, или модулем упругости второго рода:
Модуль измеряется в тех же единицах, что и модуль Е.
Таким образом, если закон Гука для растяжения постулируется при помощи соотношений (1.4) и (1.12), то для сдвига он вытекает из них как следствие.
Источник
Для того чтобы иметь представление о прочности материала, необходимо знать действующие напряжения не только в плоскости поперечного сечения, но и по любому наклонному сечению.
Рассмотрим стержень, который находится под действием растягивающей силы (рис. 29). Полагаем, что в поперечных сечениях стержня, достаточно удалённых от точек приложения сосредоточенных сил, нормальные напряжения распределяются равномерно и определяются по формуле (2.3):
.
В окрестности какой-либо точки S, лежащей в плоскости сечения abb′a′ (рис. 29), выделим бесконечно малый элемент (рис. 30а). Поскольку на грани, перпендикулярной к направлению растягивающей силы, действует нормальное напряжение , а на остальных гранях напряжения отсутствуют, то элемент находится в линейном напряжённом состоянии (главные напряжения, ). Условимся такой элемент изображать в виде плоской фигуры (рис. 30б), хотя в действительности он имеет форму прямоугольного параллелепипеда.
Определим напряжение, возникающее в наклонном сечении a1b1b1′a1′(рис. 30а,б), перпендикулярном к плоскости рисунка. Положение наклонной площадки определяется углом α между направлением главного вектора и внешней нормалью n−n к площадке. Этот угол считают положительным, если его отсчитывают против часовой стрелки от направления . Наклонную площадку обозначают углом, определяющим её положение. Так, для принятого на рис. 6.3б обозначения угла имеем α-площадку (площадка a1b1). На этой площадке будут действовать нормальное, σα и касательное τα напряжения, для определения которых применяют метод сечений. Так как наклонная площадка рассекла элемент на две части, отбросим одну из них (например, верхнюю) и рассмотрим равновесие оставшейся (нижней) части (рис. 30в). Условие равновесия запишем в виде проекций всех сил на нормаль n−n и площадку t−t:
;
где – площадь наклонного сечения.
Учитывая, что , из уравнений равновесия находим:
(6.1)
. (6.2)
Для определения напряжений на площадке, перпендикулярной к площадке a1b1 (рис. 30г), расположенной под углом ( ), заменим в формулах (6.1) и (6.2) угол α на ( ), получим:
; (6.3)
. (6.4)
Для направлений напряжений σ и τ, действующих по наклонным площадкам, принимаем следующее правило знаков: нормальное напряжение положительно, если оно растягивающее; касательное напряжение положительно, если для совпадения с его направлением нормаль к площадке необходимо повернуть по направлению движения часовой стрелки.
Отметим некоторые свойства линейного напряжённого состояния, вытекающие из зависимостей (6.1)–(6.4):
1. Сумма нормальных напряжений, действующих по двум взаимно перпендикулярным площадкам, постоянна и равна главному напряжению, т. е.
. (6.5)
Этим свойством нормальных напряжений обычно пользуются для проверки правильности их вычислений.
2. На двух взаимно перпендикулярных площадках касательные напряжения равны, но противоположны по знаку, т. е.
. (6.6)
Данное свойство является общим для любого напряжённого состояния (закон парности касательных напряжений).
3. Величина нормального напряжения в любом наклонном сечении ( ) меньше и достигает максимума лишь в поперечных сечениях ( ).
4. Касательное напряжение наибольшее значение имеет в сечении, составляющем угол с направлением . В этом случае
. (6.7)
Оценивая напряжённое состояние стержня при его осевом растяжении или сжатии, можно сделать заключение о том, что стержень разрушается либо по поперечному сечению в результате действия максимальных нормальных напряжений, либо по наклонной (под углом ) плоскости от действия наибольших касательных напряжений.
Источник
Понятие о напряжениях в точке
На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению.
Выделим в произвольной точке малую площадку ΔA, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение
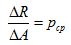
представляет собой среднее напряжение на данной площадке.
Если площадку ΔA уменьшить, то в пределе получим полное напряжение в точке
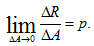
Полное напряжение р может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Проекция вектора полного напряжения р на нормаль обозначается через σ и называется нормальным напряжением.
Составляющие в плоскости сечения называются касательными напряжениями и обозначаются τ. В зависимости от расположения и наименования осей обозначения σ и τ снабжаются системой индексов.
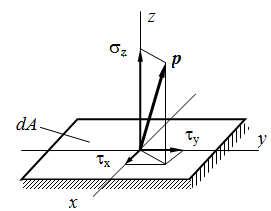
Связь между напряжениями и внутренними силами
Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA и приложим к ней элементарные силы σ dA, τx dA, τy dA.
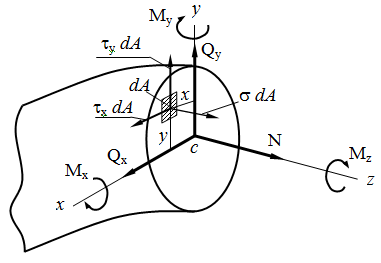
Суммируя проекции этих элементарных сил, а также их моменты относительно осей Ox, Oy, Oz, найдём;
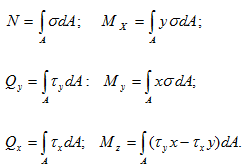
Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению.
Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например N, могут соответствовать различные законы распределения нормальных напряжений по сечению.
Одной из основных задач сопротивления материалов является задача об определении напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса.
Объемное напряженное состояние
Совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку, составляет напряженное состояние в рассматриваемой точке. На площадках общего положения действуют нормальные и касательные напряжения (рис. 3.1).
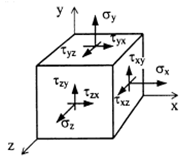
Рис. 3.1
Значения касательных напряжений на взаимно перпендикулярных площадках подчиняются закону парности касательных напряжений:
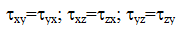
Относительные деформации и напряжения связаны обобщенным законом Гука.
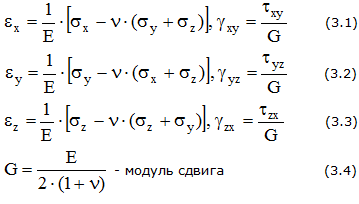
Площадки, на которых отсутствуют касательные напряжения, называются главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями (рис. 3.2).
Обозначение главных напряжений:
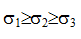
Напряженное состояние называется объемным или трехосным, если
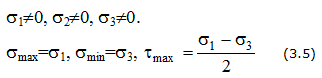
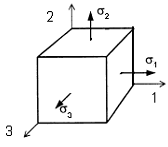
Рис. 3.2
Относительное изменение объема:
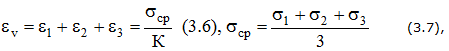
где К – модуль объемной упругости,
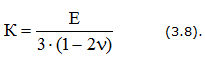
Удельная потенциальная энергия упругой деформации:
— полная
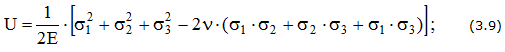
— изменение объема
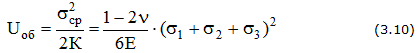
— изменение формы
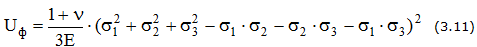
Плоское напряженное состояние
Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3).
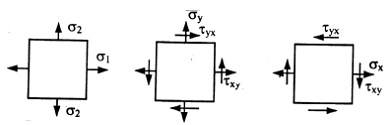
Рис.3.3
Напряжения на наклонной площадке (рис. 3.4,а)
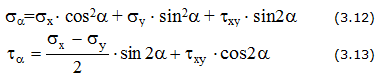
Величина и направление главных напряжений (рис. 3.4,б)
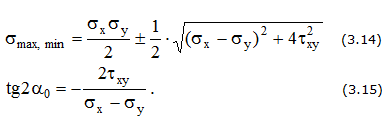
Чистый сдвиг σx = σy = 0 (рис. 3.4,в)
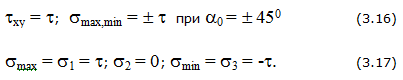
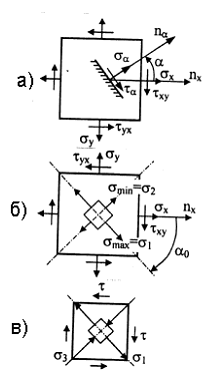
Рис. 3.4
Линейное напряженное состояние
Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю.
Проверка прочности при линейном напряженном состоянии проводится по условию прочности:
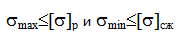
В сложном напряженном состоянии проверку прочности проводят по гипотезам прочности по эквивалентному напряжению:
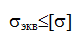
Величина σэкв определяется, исходя из принятого критерия эквивалентности, лежащего в основе одной из гипотез разрушения или гипотез прочности, при котором сложное напряженное состояние заменяется эквивалентным ему растяжением или сжатием.
Гипотезы прочности
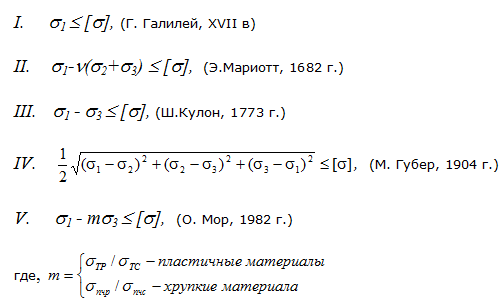
Примеры расчета напряжений >
Осевое растяжение-сжатие >
Источник
При любом напряженном состоянии наибольшие касательные напряжения будут равны
,
и действуют они в площадках равнонаклоненных к первой и третьей главным площадкам.
Когда все три главных напряжения отличны от нуля, в точке имеет место трехосное (объемное) напряженное состояние. Напряженное состояние, в котором два главных напряжения отличны от нуля, а третье равно нулю, называется двухосным (плоским) напряженным состоянием. Если только одно главное напряжение отлично от нуля, а два других равны нулю, называется одноосным (линейным) напряженным состоянием.
В общем случае напряженного состояния главные напряжения являются корнями следующего характеристического уравнения
s3 + J1 ×s2 + J2 ×s — J3 = 0,
где коэффициенты уравнения J1 = sx + sy + sz,
J2 = sx × sy + sy × sz + sz × sx — tху2 — tух2 — tzх2,
J3 = sx × sy × sz — sx × t уz2 — sy × tzх2 — sz × tху2 + 2 × tху × tуz × tzх
являются первым, вторым и третьим инвариантами тензора напряжений.
4.2. Двухосное напряженное состояние
При расчетах стержней наиболее часто приходится иметь дело с двухосным (плоским) напряженным состоянием. Поэтому рассмотрим этот случай более подробно.
При двухосном напряженном состоянии J3 = 0 и характеристическое уравнение принимает вид
s × (s2 — J1 × s + J2) = 0.
Откуда видно, что одно главное напряжение равно нулю, в стержнях это s2, а два других найдем по формуле
s1,3 = 0,5 × .
Поскольку в стержнях sХ = sу = 0, то J1 = sz, а J2 = — t2. Таким образом, получаем
s1,3 = 0,5 × .
Положение второй главной площадки всегда известно. Это одно из продольных сечений стержня. Две других главных площадки будут перпендикулярны ей, а углы между нормалями к этим площадкам и осью Х или У определятся по формулам
tg a 1 = s1/tzх; tg a2 = s3/tzх.
4.3. Одноосное напряженное состояние
При растяжении стержня, а также в крайних точках сечения стержня при изгибе имеет место одноосное напряженное состояние. В этих точках сечении стержня возникают, только нормальные напряжения и в зависимости от знака это будет соответственно:
s1 = + s z, s2 = 0, s3 = 0,
или s1 = 0, s2 = 0, s3 = — sz.
Таким образом, положение главных площадок заранее известно: это поперечное сечение и два продольных сечения. В сечениях же наклонных к указанным будут возникать и нормальные и касательные напряжения. Если обозначить угол между осью стержня (осью z) и нормалью к наклонному стержню через a, то выражения для нормальных и касательных напряжений в этом сечении будут
sa = sz × cos2 a, ta = .
При повороте площадки на угол p/4 касательные напряжения достигают наибольшего значения tmax = sz/2. Нормальные напряжения в этой площадке
sa = sz/2.
4.4. Обобщенный закон Гука
На основании принятой гипотезы об идеальной линейной упругости материала стержня деформации в точке стержня пропорциональны напряжениям. А если учесть и гипотезу об изотропности материала, то получим следующие соотношения, которые связывают напряжения и упругие деформации при сложном напряженном состоянии:
;
;
,
где eх, eу, ez – линейные деформации в направлении координатных осей;
gху, gyz, gzx – угловые деформации или угол сдвига в точке;
Е – модуль упругости первого ряда или модуль Юнга. Для стали можно принимать Е = 2 × 1011 Па;
G – модуль сдвига, для стали – G = 8 × 1010 Па;
m – коэффициент поперечной деформации или коэффициент Пуассона. Для металлов можно брать m = 0,3.
Эти формулы выражают обобщенный закон Гука.
Коэффициент Пуассона численно равен отношению поперечной деформации к продольной. Для стержней:
.
Так как в стержнях sх = sу = 0, то формулы закона Гука примут вид
eх = ey = — m × sz /E; ez = sz /E.
5. Напряжения в поперечных сечениях стержня
5.1. Нормальные напряжения в стержнях
В зависимости от вида внешних нагрузок в поперечных сечениях стержня могут возникать и нормальные, и касательные напряжения.
Если в поперечном сечении стержня продольная сила N и изгибающие моменты Мх и Му не равны нулю, то на основании интегральных зависимостей (гл. 2) в точках этого поперечного сечения возникают нормальные напряжения. В поперечных сечениях прямых стержней эти напряжения можно вычислять по следующей формуле
где F – площадь поперечного сечения, х, у – координаты точки, в которой определяется напряжение, относительно главных центральных осей.
Эта формула выведена относительно главных центральных осей поперечного сечения. Поэтому величины, стоящие в знаменателе, Jx и Jy есть главные центральные моменты инерции поперечного сечения. Порядок вычисления этих характеристик описан в главе 1.
Из формулы видно, что напряжения есть функция двух координат, следовательно, эпюра функции напряжений будет представлять собой некоторую плоскость, наклоненную к плоскости поперечного сечения и пересекающую его по некоторой линии. Нормальные напряжения в точках этой линии будут равны нулю, и она называется нулевой линией.
Очевидно, что наибольшие напряжения будут возникать в точках, наиболее удаленных от нулевой линии.
Уравнение нулевой линии относительно главных центральных осей:
.
С одной стороны от нулевой линии волокна стержня будут растянуты, а с другой – сжаты, то есть напряжения будут иметь разный знак.
В частных случаях нагружения в поперечном сечении стержня могут возникать не все внутренние силовые факторы.
5.2. Растяжение (сжатие)
Это такой вид нагружения, когда в поперечном сечении действует только продольная сила N ≠ O, остальные внутренние силы равны нулю. В этом случае нормальные напряжения во всех точках поперечного сечения будут одинаковы, и определяются по формуле sz = N/F.
Это самый рациональный способ нагружения стержня. Все точки поперечного сечения – равноопасны и в них имеет место одноосное напряженное состояние. При растяжении N > 0, sz > 0, тогда s1 = sz, s2 = 0, s3 = 0. При сжатии N < 0, sz < 0, тогда s3 = sz, s1 = s2 = 0.
5.3. Прямой изгиб
В этом случае нагружения только один из изгибающих моментов равен нулю. Пусть это будет Мх ≠ O, тогда формула для определения нормальных напряжений будет
sz = .
В этом случае нулевая линия будет совпадать с осью Х ( при у = 0; sz = 0).
Наибольшее напряжения будут возникать в точках наиболее удаленных от оси Х, когда у = уmax
szmax = .
Отношение Jx/ymax есть величина постоянная для данного сечения. Её обозначают Wх и называют осевой момент сопротивления.
Также как и для геометрических характеристик плоских фигур, так и для осевых моментов сопротивления, формулы можно найти в справочниках. Моменты сопротивления прокатных профилей проведены в таблицах ГОСТ.
Следовательно, нормальные наибольшие напряжения в поперечных сечениях стержня при прямом изгибе можно вычислить по формуле
sz = Мх/Wх.
5.4. Косой изгиб
Косым изгибом называется такой вид нагружения, когда оба изгибающих момента отличны от нуля Мх ¹ 0; Му ¹ 0, а продольная сила N = 0.
Нормальные напряжения при косом изгибе:
sz = .
Уравнение нулевой линии:
y = .
Это уравнение прямой, проходящей через начало координат. Тангенс угла наклона этой прямой к оси Х:
tga = .
Опасными точками будут являться точки, наиболее удаленные от нулевой линии.
5.5. Растяжение с изгибом
В этом случае продольная сила и один изгибающий момент отличны от нуля
Мх ¹ 0, N ¹ 0. Формула для определения нормальных напряжений примет вид
Уравнение нулевой линии:
.
Это прямая параллельная оси Х, лежащая выше или ниже оси на расстоянии
ay = N × Jx/Mx × F.
Опасными также будут точки, наиболее удаленные от нулевой линии.
5.6. Касательные напряжения при поперечном изгибе стержня
Если в поперечном сечении стержня изгибающий момент и поперечная сила не равны нулю Mx ¹ 0, Qy ¹ 0, то такой вид нагружения называется поперечным изгибом. Из интегральных зависимостей:
следует, что в точках поперечного сечения будут возникать нормальные и касательные напряжения. На основании принятой гипотезы плоских сечений нормальные напряжения следует определять по формуле
sz = ,
а касательные напряжения определяют по формуле Журавского:
,
где Qy – поперечная сила в рассматриваемом сечении;
Jx – главный центральный момент инерции сечения;
b(y) – ширина поперечного сечения в том месте, где определяют касательное напряжение;
– статический момент отсеченной части поперечного сечения.
За отсеченную часть принимают часть поперечного сечения, лежащая ниже или выше линии параллельной оси Х и проходящей через точку, в которой находят касательное напряжение.
На рисунке 5.1 показано произвольное сечение с главными, центральными осями ХУ. Для того, чтобы определить касательное напряжение tzy в точке А, проводим через эту точку прямую параллельную оси Х. Длина этой линии и будет шириной b(y). Сечение оказывается рассеченным на две части F1 и F2 с центрами тяжести С1 и С2.
За отсеченную часть можно принять лю —
бую из этих частей, так как
= F1× у1 = F2 × у2.
При расчетах за отсеченную обычно выбирают ту часть, для которой проще вычислить статический момент.
Если ширина сечения постоянна (прямоугольное сечение), то наибольшее касательное напряжение возникает в точках на оси Х. Если же ширина сечения меняется по высоте, то в этом случае касательные напряжения достигают наибольшей величины, там, где ширина сечения наименьшая. В крайних верхних и нижних точках, а также в угловых точках, касательные напряжения равны нулю.
Если сечение составлено из прокатных профилей, то при вычислении статического момента следует считать, что каждая часть профиля представляет собой прямоугольник, то есть не учитывать закругления.
5.7. Касательные напряжения при кручении стержня
Рассматриваем только кручение стержней круглого и кольцевого поперечного сечения.
Полное касательное напряжение t всегда будет направлено перпендикулярно радиусу вектора r точки, в которой определяется напряжение.
Касательные напряжения в произвольной точке
,
где — полярный момент поперечного сечения.
Для круга = p × d4/32 = 0,1× d4.
В точках, лежащих на контуре, напряжения достигают наибольшего значения:
,
где = Jr/rmax – полярный момент сопротивления.
Для круга = p × d3/16 = 0,2× d3.
Поскольку нормальные напряжения в точках поперечного сечения отсутствуют, то в них имеет место s напряженное состояние чистого сдвига, при котором s1 = t; s2 = 0; s3 = -t.
6. Расчет стержней на прочность
6.1. Основные механические характеристики материалов.
Допускаемые напряжения
Для определения характеристик прочности материала проводят испытание образцов на растяжение. При этом в рабочей части образца будет одноосное напряженное состояние. В процессе испытания определяют следующие механические характеристики материала: предел пропорциональности sп, предел упругости sу, предел текучести sт, и временное сопротивление разрыву или предел прочности sв. Для деталей, изготовленных из пластичных материалов, опасным считают предел текучести sт, а для деталей из хрупких материалов – предел прочности sв. Эти напряжения будем считать предельными slim. Для расчетов на прочность их следует уменьшить настолько, чтобы в эксплуатационных условиях действующие напряжения всегда были меньше предела упругости.
Таким образом, получают допускаемое напряжение
[s] = slim/n,
где slim – предельное напряжение (sт или sв);
n – коэффициент запаса прочности, показывающий во сколько раз допускаемое напряжение меньше опасного.
В зависимости от материала и условий эксплуатации коэффициент запаса прочности может измениться в пределах 1,5 ¸ 3,0.
6.2. Расчет на прочность при одноосном напряженном состоянии
Если в опасной точке стержня, независимо от вида нагружения, имеет место одноосное напряженное состояние, то, очевидно, что материал в этой точке будет вести себя также как в растягиваемом образце. Следовательно, опасными напряже-ниями будут: предел текучести sт – при пластическом состоянии материала или предел прочности sв – при хрупком состоянии материала:
slim = sт,
или slim = sв.
По опасным напряжениям устанавливают допускаемые напряжения [s], обеспечивая известный коэффициент запаса против наступления предельного состояния. Таким образом, условия прочности для одноосного напряженного состояния примет вид
s1 £ [s] или ½s3½£ [s] . (6.1)
Поскольку речь идет о расчете стержней, то в зависимости от знака максимального напряжения главные напряжения будет равны s1 = szmax или s3 =
= szmax и, следовательно, условие прочности (6.1) примет вид
½s zmax ½ £ [s].
При растяжении szmax = .
При изгибе szmax = Мхmax/£ [s].
При расчетах на прочность стержней приходится решать следующие задачи:
1. Заданы внешние нагрузки, схема нагружения, форма поперечного сечения, размеры поперечного сечения. Требуется определить размеры поперечного сечения.
2. Заданы размеры и форма поперечного сечения стержня, схема нагружения. Требуется подобрать допускаемую нагрузку.
3. Заданы нагрузки и все размеры стержня. Известно допускаемое напряжение для материала стержня. В этом случае необходимо произвести проверочный расчет, то есть выполняется или нет условие прочности для стержня при заданных условиях.
6.3. Расчет на прочность при сложном напряженном состоянии
Пусть в некоторой точке стержня два или все три напряжения s1, s2, s3, не равны нулю. В этом случае, как показывают опыты, для одного и того же материала опасное состояние может наступить при различных предельных значениях главных напряжениях в зависимости от соотношения между ними. Поэтому экспери-ментально установить величины главных напряжений очень сложно.
Другой путь решения задачи заключается в установлении критерия прочности. Для этого вводят гипотезу о преимущественном влиянии на прочность материала того или иного фактора: полагают, что нарушение прочности материала при любом напряженном состоянии наступит только тогда, когда величина выбранного фактора достигнет некоторого предельного значения. Таким образом, введение критерия прочности позволяет составить данное сложное напряженное состояние с одноосным напряженным состоянием, равноопасным заданному.
Единственное главное напряжение одноосного напряженного состояния в этом случае называют эквивалентным sэкв или расчетным sрасч.
Таким образом, расчет на прочность сложного напряженного состояния заменяем расчетом на прочность равноопасного ему одноосного напряженного состояния, условия прочности для которого уже известно. Следовательно, условие прочности для сложного напряженного состояния можно записать в виде sэкв. £ [s] .
Выбранная указанным образом гипотеза обычно называется механической теорией прочности.
В инженерной практике наиболее часто используется теория наибольших касательных напряжений и энергетическая теория прочности. Согласно первой
sэкв = s1 — s3, (6.2)
по второй
sэкв = . (6.3)
Эти две теории хорошо подтверждаются опытами для материалов, одинаково работающих на растяжение и сжатие, каким можно считать стиль.
Преобразуем формулы (6.2) и (6.3) применительно к расчету стержней.
В опасных точках стержней, согласно принятым гипотезам, напряженное состояние может быть только двухосным, при котором
s2 = 0,
s1 = ,
s3=.
После подстановки s1 и s3 в формулы (6.2) и (6.3) получаем по теории наибольших касательных напряжений
sэкв = ,
по энергетической теории
sэкв = .
Как видно, разница между величинами эквивалентного напряжения, вычислен-ного по приведенным теориям прочности, незначительна.
6.4. Расчет валов на прочность
Рассмотрим подробнее расчет на прочность стержня круглого поперечного сечения, подверженного изгибу в двух плоскостях и кручению, то есть в поперечном сечении стержня Мх ≠ 0, Му ≠ 0, Мz ≠ 0.
Поскольку любой диаметр для круга является осью симметрии и, следовательно, главной центральной осью. Поэтому изгибающие моменты Мх и Му можно привести к равнодействующему Мизг = . Тогда нормальное наибольшее напряжение в одной из точек контура сечения, можно вычислить по формуле
| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 |
Источник

