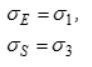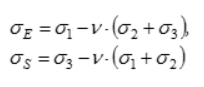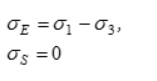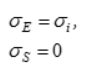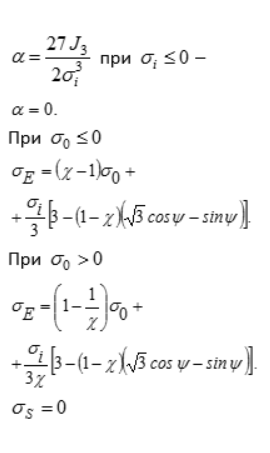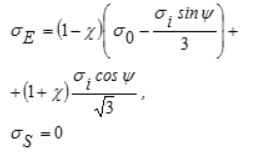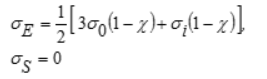Лира грунт предельное напряжение растяжения

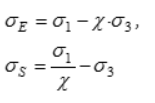
Расчётчик всегда должен помнить, что все расчётные функции, реализованные в любом программном комплексе, имеют под собой теоретическую основу, поэтому тема сегодняшней заметки посвящается теории расчёта эквивалентных напряжений.

В расчетах на прочность при простых напряженных состояниях, в частности, при одноосном напряженном состоянии и состоянии чистого сдвига, задача является сравнительно простой, так как эти напряженные состояния воспроизводятся при испытаниях на растяжение и на кручение стержней. Об опасности действующих напряжений можно судить, сопоставляя их с экспериментально полученным пределом текучести для пластических материалов или с временным сопротивлением для хрупких. Но чаще напряженное состояние является сложным. Технически невозможно проводить испытания материалов при сложном напряженном состоянии из-за бесконечного числа этих напряженных состояний. Поэтому ученые мужи выбрали другой путь решения данной задачи: сведении сложного напряженного состояния к эквивалентному ему простому — одноосному и сравнение эквивалентного напряжения с предельным одноосным, определяемым экспериментально. При сведении сложного напряженного состояния к эквивалентному обычно используется некоторый критерий прочности – теории прочности, которые дают возможность находить эквивалентное напряженное состояние как функцию одного, двух или всех трех главных напряжений.

К сожалению, наука не смогла определить истинную причину разрушения материалов, поэтому единой общей теории прочности не существует, есть много разрозненных теорий, каждая из которых базируется на своем критерии разрушения материала.

Для удобства все теории, позволяющие произвести расчёт эквивалентных напряжений и их характеристик, реализованные в ЛИРА 10.6, сведены в таблицу 1.

№ п/п	Наименование теории прочности	Формула	Геометрическая интерпретация		Примечания
1	2	3	4		5
1	Наибольших главных напряжений		Куб с центром, смещенным относительно начала координат в сторону гидростатического давления		Исторически первая теория прочности – предложенная Г. Галилеем. Удовлетворительно описывает предельное состояние весьма хрупких, достаточно однородных материалов, таких как стекло, гипс, некоторые виды керамики
2	Наибольших главных деформаций		Равносторонний косоугольный параллелепипед с осью симметрии, равнонаклоненной к координатным осям		Предложена Э. Мариоттом и развита Б. Сен-Венаном. Ввиду малой достоверности в настоящее время почти не применяется
3	Наибольших касательных напряжений		Правильная шестигранная призма, равно наклоненная к осям координат		Предложена Ш. Кулоном. Удовлетворительно описывает предельное состояние пластичных малоупрочняющихся материалов (отпущенные стали), для которых характерна локализация пластических деформаций
4	Энергетическая		Круговой цилиндр, описанный вокруг призмы, интерпретирующей теорию максимальных касательных напряжений		Предложена М.Губером, Г. Генки, Р.Мизесом. Хорошо описывает предельное состояние широкого класса пластичных материалов (медь, никель, алюминий, углеродистые и хромоникелевые стали)
5	Теория О. Мора		Шестигранная равнонаклоненная к осям пирамида		Применяется для установления предельного состояния достаточно однородных материалов, по разному сопротивляющихся растяжению и сжатию
6	Друккера – Прагера		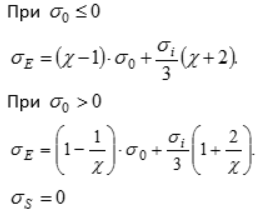Двуполостной параболоид вращения, равнонаклоненный к осям координат		Удовлетворительно описывает предельное состояние сравнительно пластичных материалов, для которых параметр
7	Писаренко – Лебедева		Коническая поверхность, описанная вокруг пирамиды Мора. В сечении октаэдрической плоскостью – равносторонний криволинейный треугольник		Хорошо описывает предельное состояние широкого класса достаточно однородных конструкционных материалов. При преобразуется в энергетическую теорию. В случае, когда (весьма хрупкие материалы), результаты вычислений практически совпадают с данными расчета по теории наибольших главных напряжений
8	Гениева		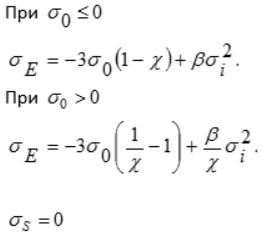—	Хорошо описывает предельное состояние бетона
9	Кулона – Мора		—	Грунт
10	Боткина		—	Грунт

Условные обозначения

σE — эквивалентное напряжение при растяжении;
σS — эквивалентное напряжение при сжатии;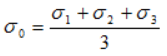
— среднее напряжение
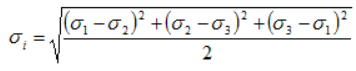— интенсивность напряжений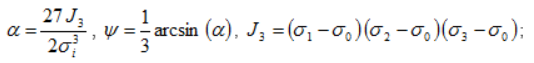

Rt, Rc — предельные напряжения растяжения и сжатия, для грунтов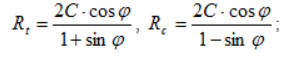

С — сцепление;
φ — угол внутреннего трения;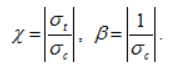

Стоит отметить, что описанные выше теории расчёта эквивалентных напряжений реализованы в ЛИРА 10.6 для пластинчатых и объемных элементов, узнать о расчете напряжений в стержнях можно в соответствующей заметке.

Использованная литература:

Писаренко Г. С. Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, В. В. Матвеев. – Киев: Наукова думка, 1988. – 736 с.

Источник

Общие сведения о результатах расчёта стальных конструкций

ПК ЛИРА-САПР позволяет выполнять расчёты основных типов стальных конструкций: ферм, балок и колонн.

Для каждого типа конструкции выполняется проверка или подбор сечения элемента по трём группам критериев:

Первое предельное состояние (1ПС);
Второе предельное состояние (2ПС);
Местная устойчивость (МУ);

Кнопки для отображения результатов проверки или подбора сечения по каждой из трёх групп критериев расположены на ленте, закладка «Сталь».

Результаты_расчета_СТК_01.png

Местоположение кнопок для отображения результатов расчётов стальных конструкций не ленте ЛИРА САПР

Вышеуказанные команды позволяют отобразить максимальные результаты проверки сечения или его подбора, которые, в свою очередь, выбираются из всех выполняемых проверок для каждого типа элемента и каждой группы критериев. Кнопки для отображения результатов по каждому из критериев расположены на вкладке «Сталь», в группе команд «Результаты расчёта по сечениям»

Результаты_расчета_СТК_02.png

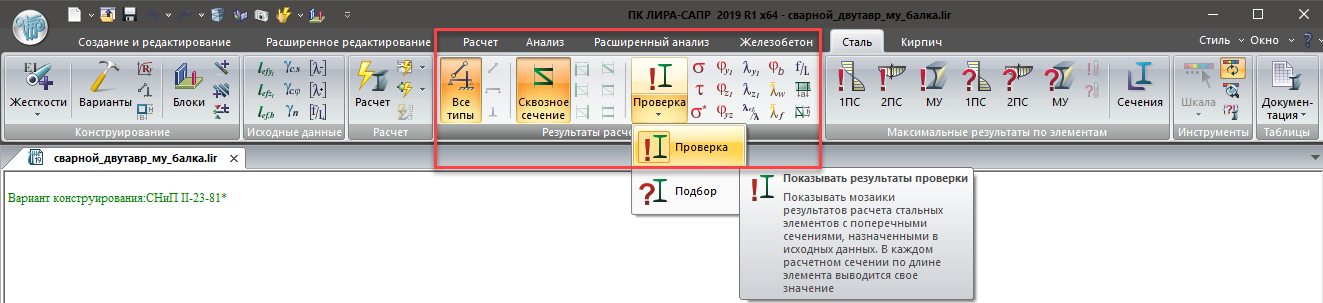
Местоположение кнопок для отображения результатов расчётов стальных конструкций по сечениям не ленте ЛИРА САПР

Важно: результаты по сечениям формируются на основании принятого количества расчётных сечений в каждом стержне. Как назначить расчётные сечения стержней см. в статье https://rflira.ru/kb/3/112/

Рассмотрим, как формируются результаты стального расчёта на примере конструкций сплошного сечения.

Результаты расчёта элементов тип «Ферменный»

При расчёте центрально-сжатых элементов выполняется определение процентов использования по 1ПС, 2ПС и МУ.

Первое предельное состояние (1ПС):

Нормальные напряжения;
Устойчивость относительно оси Y1;
Устойчивость относительно оси Z1;
Устойчивость в двух плоскостях;

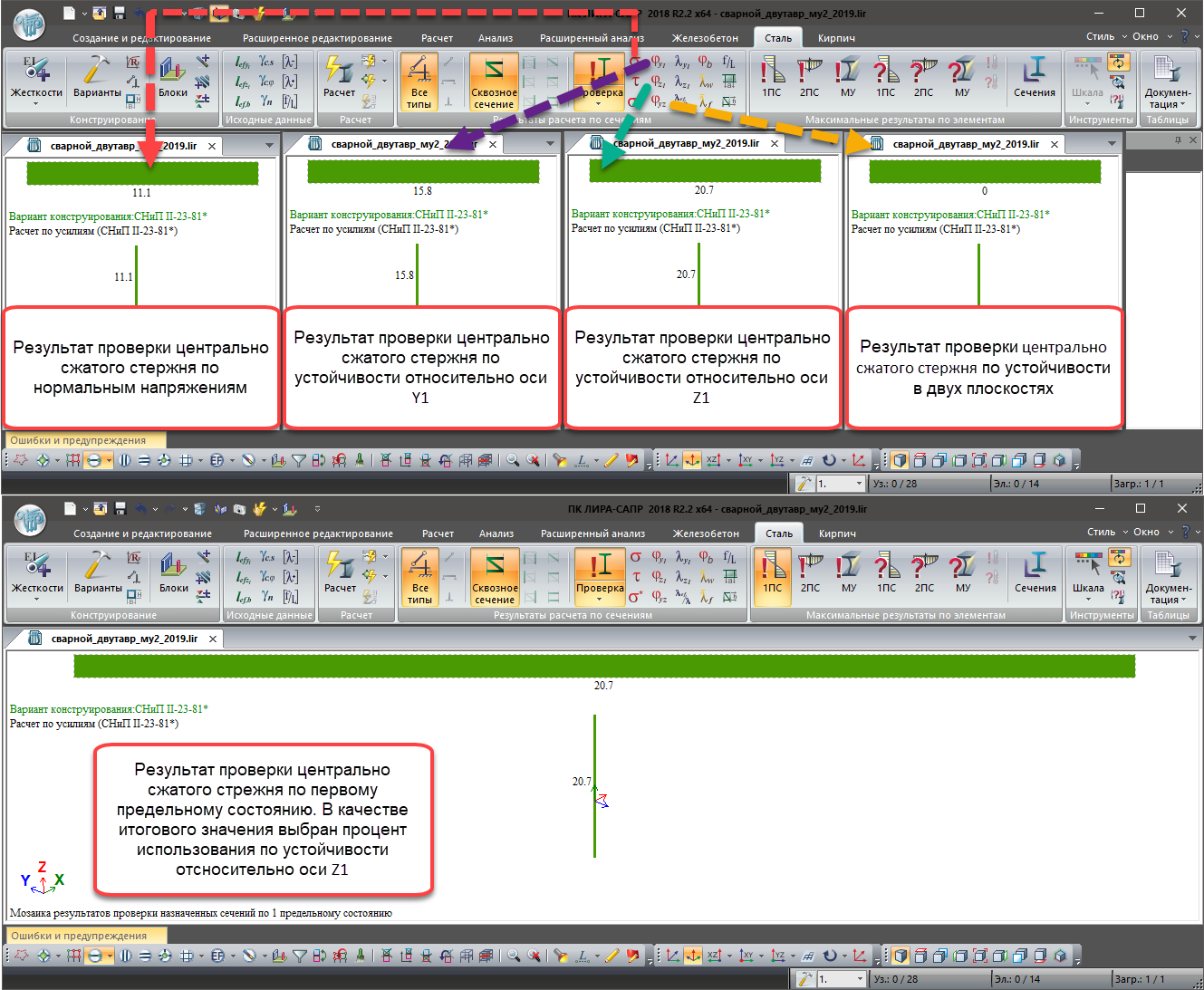
Результаты_расчета_СТК_03.png

Результаты проверки центрально-сжатого стержня по критериям первой группы предельных состояний

Второе предельное состояние (2ПС):

Гибкость относительно оси Y1;
Гибкость относительно оси Z1;

Результаты_расчета_СТК_04.png

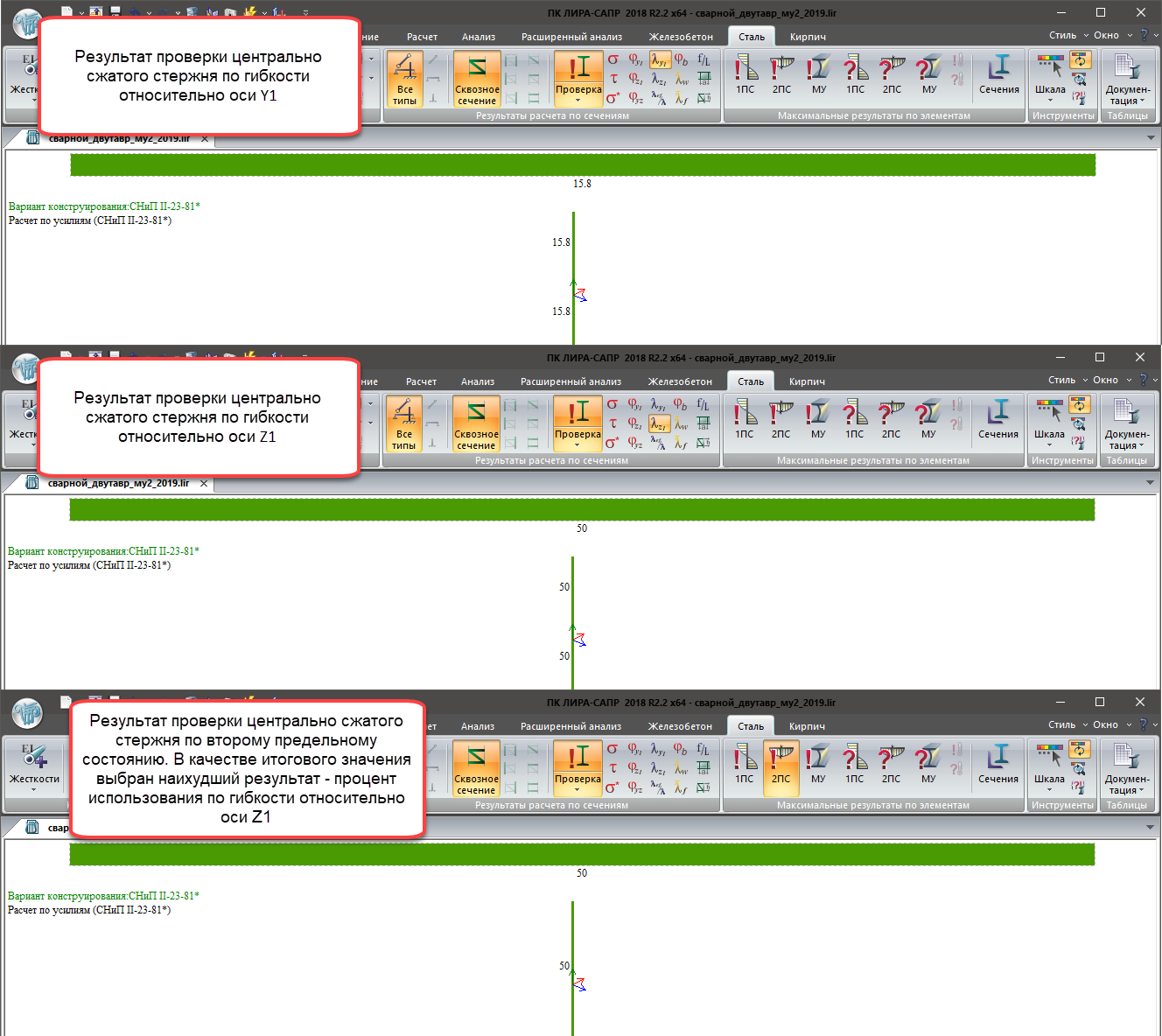
Результаты проверки центрально-сжатого стержня по критериям второй группы предельных состояний

Важно: в результатах проверки элемента по гибкости показано значение в процентах использования элемента по данному критерию.

Местная устойчивость (МУ):

Устойчивость стенки;
Устойчивость пояса;

Результаты_расчета_СТК_05.png

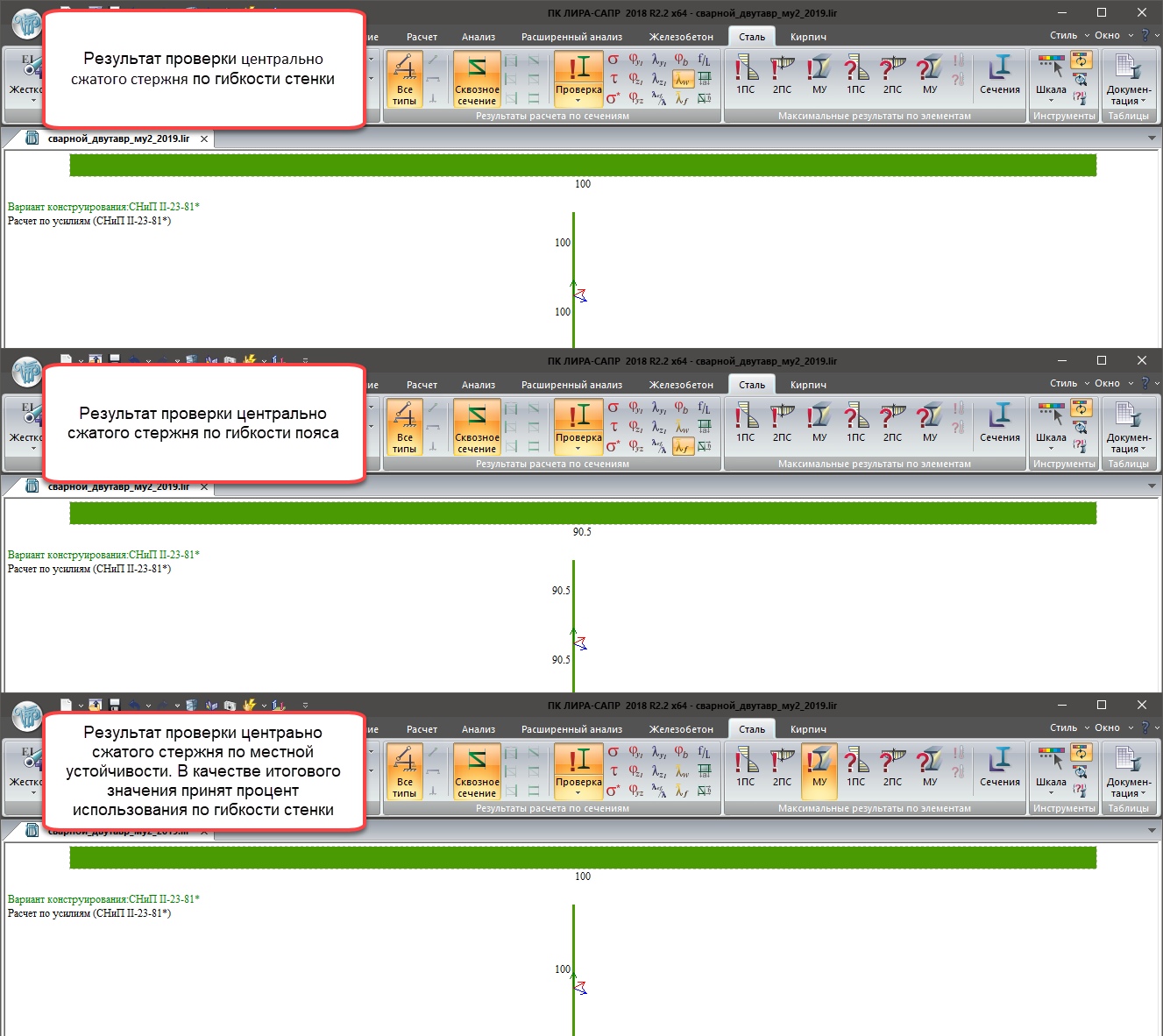
Результаты проверки центрально-сжатого стержня по критериям местной устойчивости

Результаты расчёта элементов тип «Балка»

При расчёте изгибаемых элементов выполняется определение процентов использования по 1ПС, 2ПС и МУ.

Первое предельное состояние (1ПС):

Нормальные напряжения;
Касательные напряжения;
Приведённые напряжения;
Общая устойчивость;

Результаты_расчета_СТК_06.png

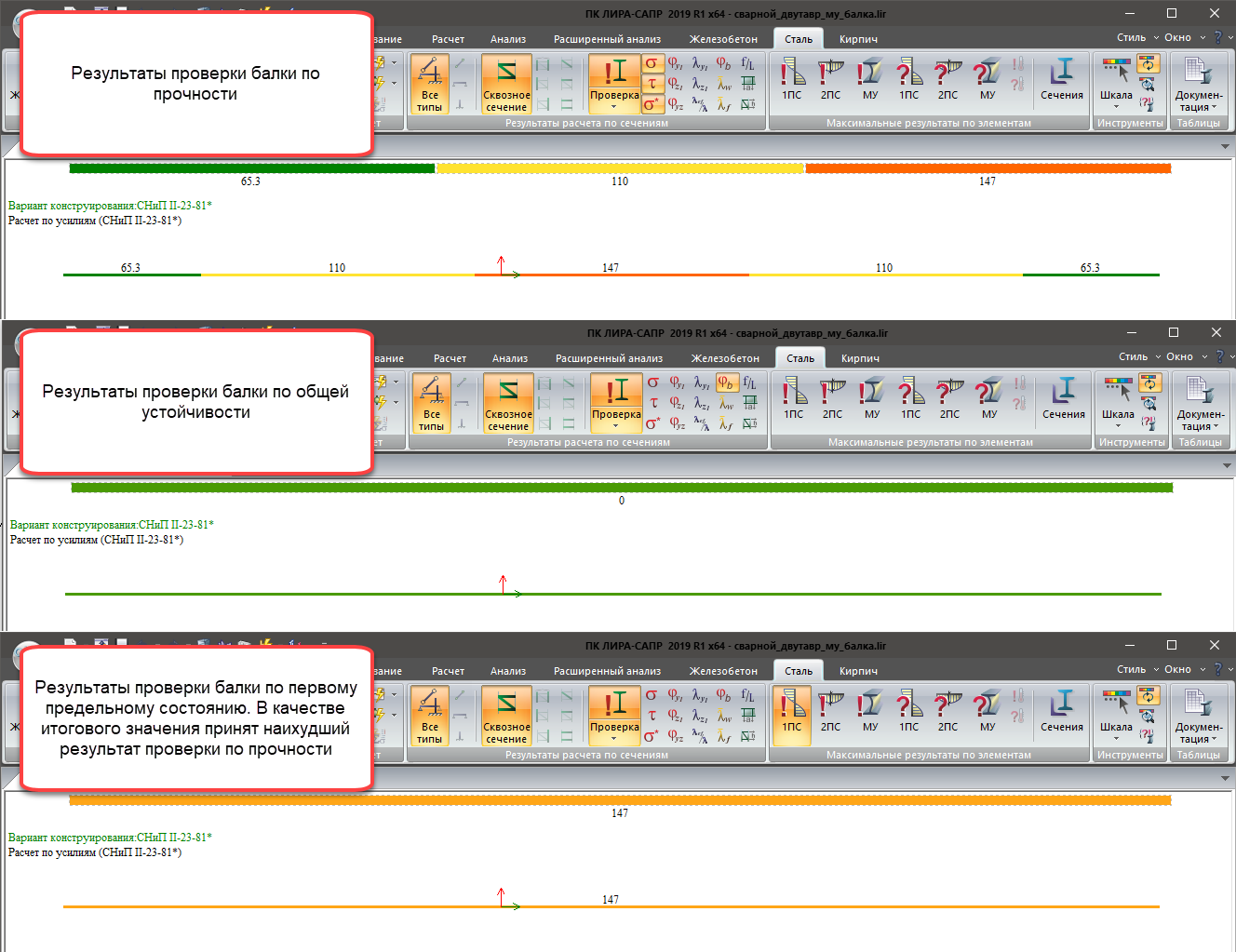
Результаты проверки изгибаемого стержня по критериям первой группы предельных состояний

Второе предельное состояние (2ПС):

Относительный прогиб;
Наименьший коэффициент поперечного изгиба;

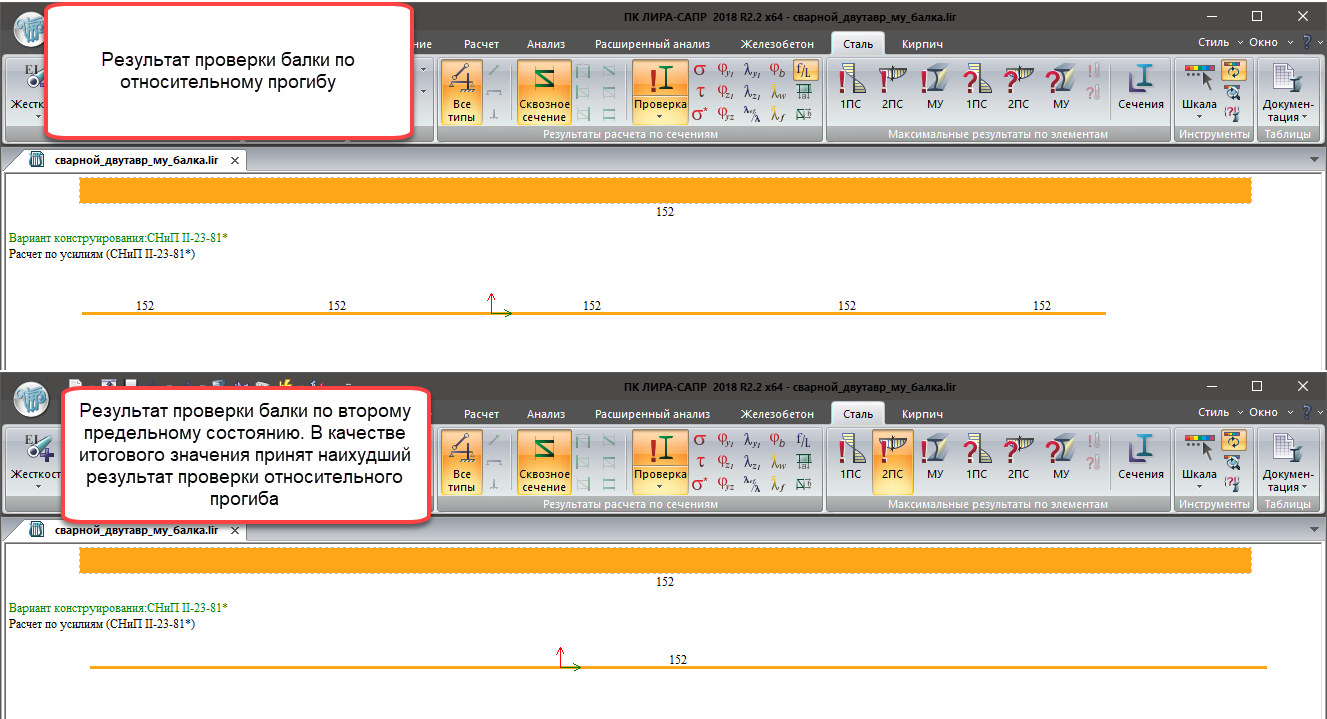
Результаты_расчета_СТК_07.png

Результаты проверки изгибаемого стержня по критериям второй группы предельных состояний

Местная устойчивость (МУ):

Устойчивость стенки;
Устойчивость пояса;

Результаты_расчета_СТК_08.png

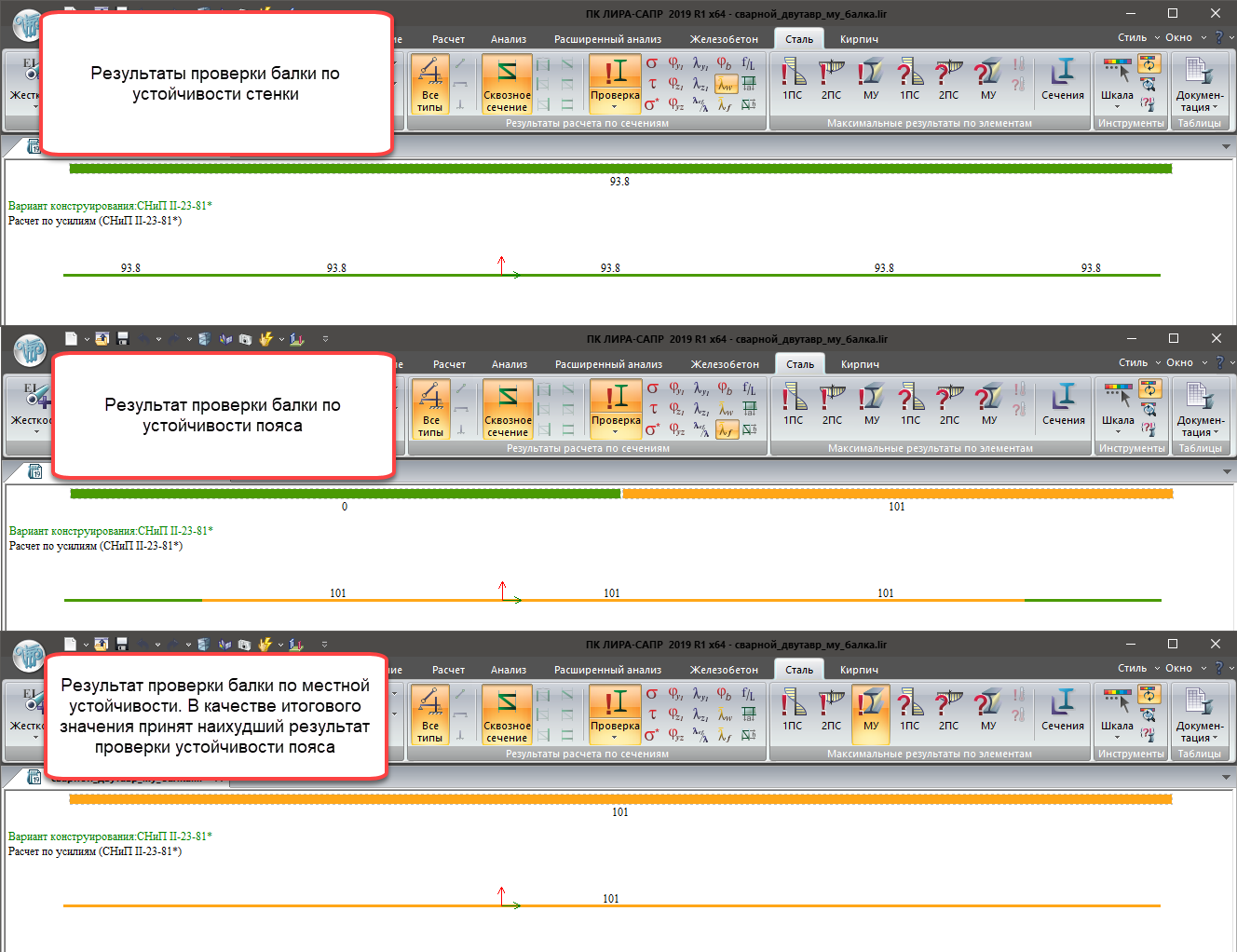
Результаты проверки изгибаемого стержня по критериям местной устойчивости

В качестве итогового значения по 1ПС, 2ПС, МУ, выбирается наихудший результат.

Результаты расчёта элементов тип «Колонна»

При расчёте внецентренно-сжатых элементов выполняется определение процентов использования по 1ПС, 2ПС и МУ.

Первое предельное состояние (1ПС):

Нормальные напряжения;
Касательные напряжения;
Приведённые напряжения;
Устойчивость относительно оси Y1;
Устойчивость относительно оси Z1;
Устойчивость в двух плоскостях

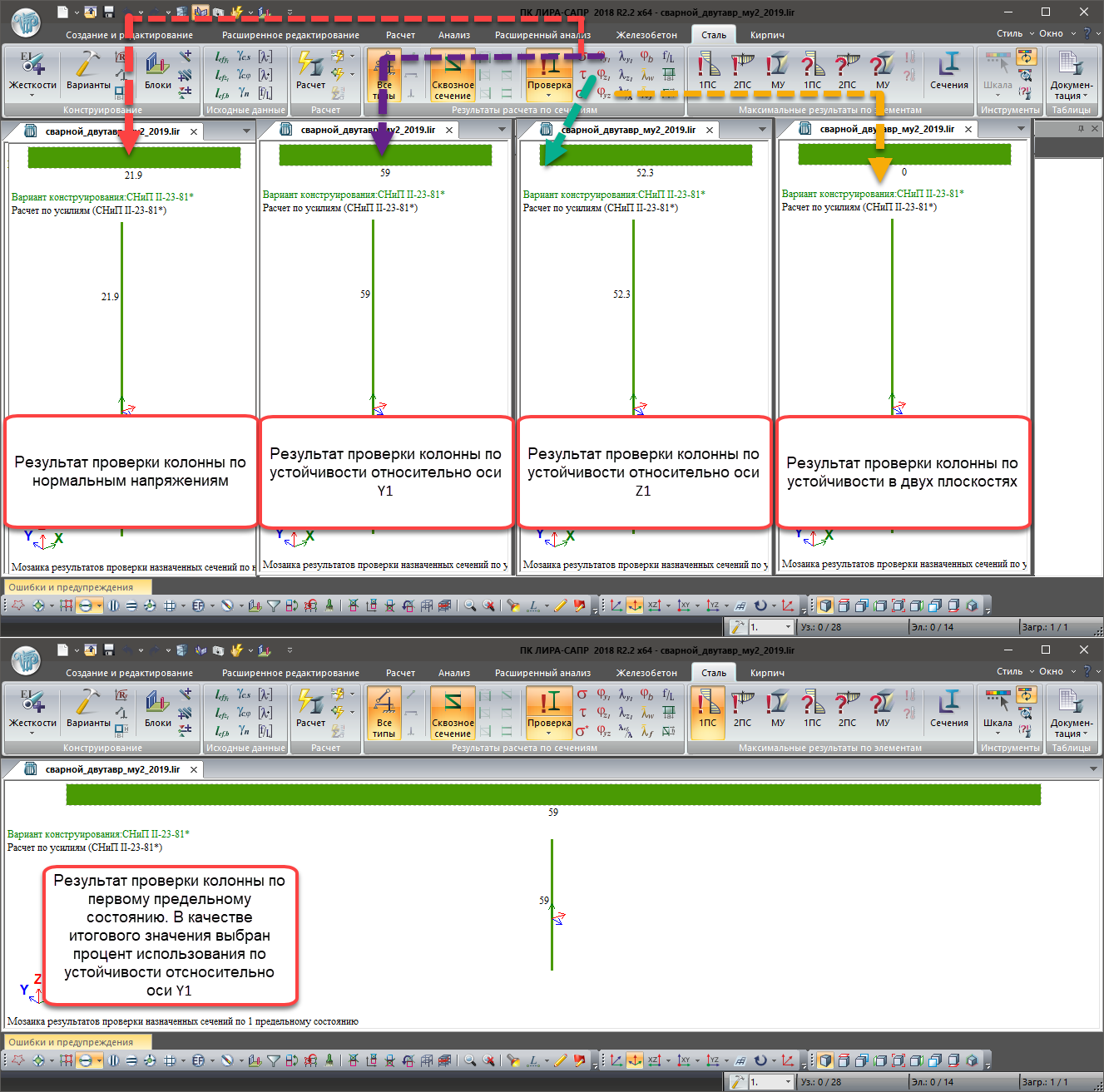
Результаты_расчета_СТК_09.png

Результаты проверки внецентренно-сжатого стержня по критериям первой группы предельных состояний

Второе предельное состояние (2ПС):

Гибкость относительно оси Y1;
Гибкость относительно оси Z1;

Результаты_расчета_СТК_10.png

Результаты проверки внецентренно-сжатого стержня по критериям второй группы предельных состояний

Местная устойчивость (МУ):

Устойчивость стенки;
Устойчивость пояса;

Результаты_расчета_СТК_11.png

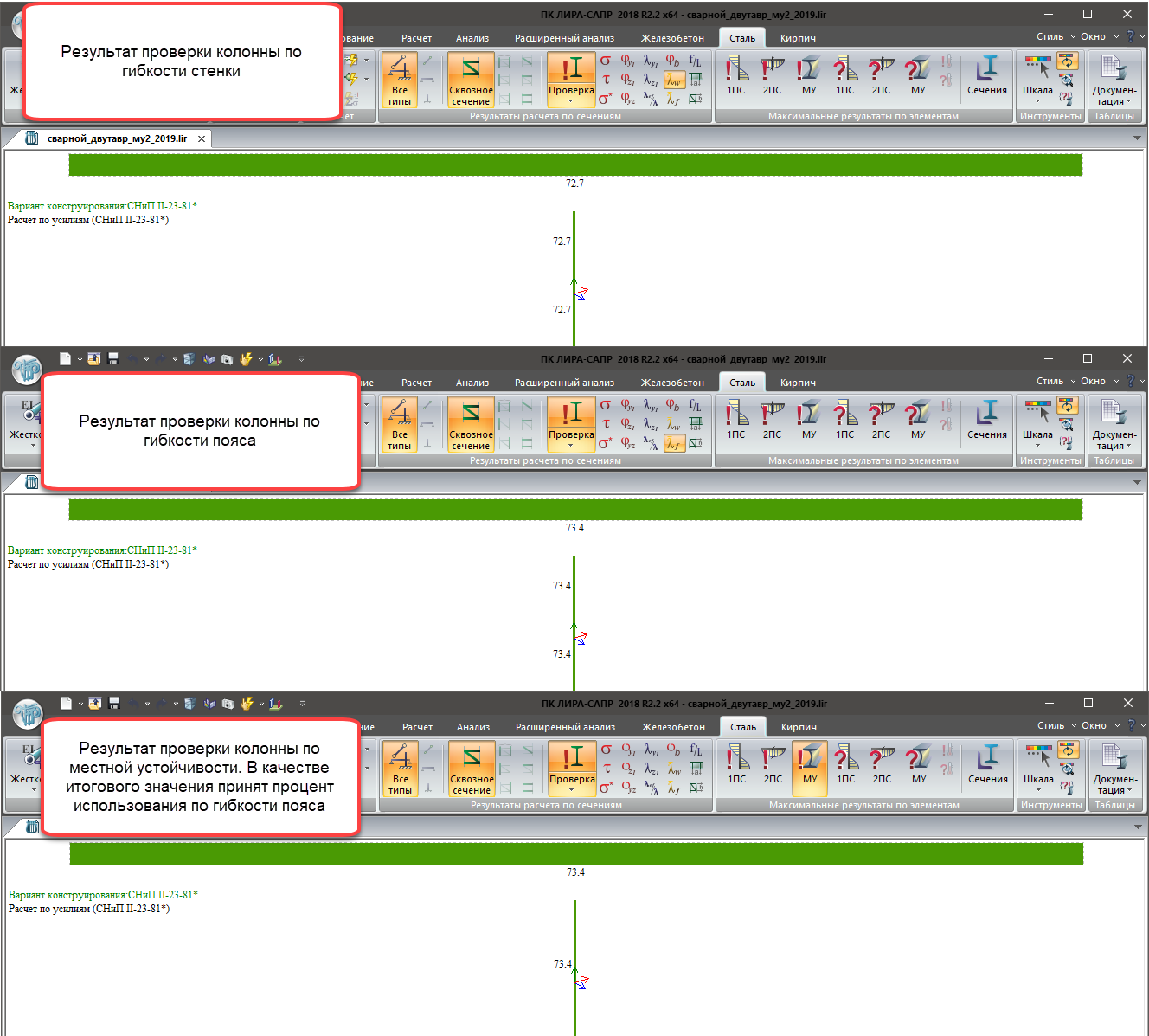
Результаты проверки внецентренно-сжатого стержня по критериям местной устойчивости

Источник

Рекомендации по применению разных признаков схемы и типов стрежневых КЭ для решения задач в ЛИРА САПР

Теоретические предпосылки

Признаки схемы

В ПК ЛИРА-САПР, при создании новой задачи, требуется выбрать признак схемы. Всего признаков схемы шесть (в версии 2018 и старше):

Признак 1 — схемы, располагаемые в плоскости XOZ; каждый узел имеет 2 степени свободы – линейные перемещения вдоль осей X, Z или X2, Z2
Признак 2 — схемы, располагаемые в плоскости XOZ; каждый узел имеет 3 степени свободы – линейные перемещения вдоль осей X, Z или X2, Z2 и поворот вокруг оси Y или Y2
Признак 3 — схемы, располагаемые в плоскости XOY; каждый узел имеет 3 степени свободы – линейное перемещение вдоль оси Z или Z2 и повороты вокруг осей X, Y или X2, Y2
Признак 4 — пространственные схемы, каждый узел которых имеет 3 степени свободы – линейные перемещения вдоль осей X, Y, Z или X2, Y2, Z2.
Признак 5 — пространственные схемы общего вида с 6 степенями свободы в узле.
Признак 6 — пространственные схемы общего вида с 7 степенями свободы в узле. То же что и Признак 5, но с дополнительной степенью свободы W — депланация сечения стержня.

Теоретически признак схемы 5 (шесть степеней свободы в узле) применим для подавляющего большинства расчётных моделей, однако использование только данного признака схемы, вызывает необходимость соответствующим образом дорабатывать расчётные модели, для обеспечения их корректной работы.

В данной статье будут даны рекомендации по применению различных признаков схем для решения разных типов задач с целью экономии времени на создание модели.

Тип конечного элемента

Перечень типов конечных элементов (типов КЭ) представлен в Библиотеке КЭ в соответствующем разделе справки ЛИРА САПР.

При составлении стержневых моделей, в подавляющем большинстве случаев, используется тип КЭ10 – Универсальны пространственный стержневой КЭ, имеющий шесть степеней свободы в узле. Повсеместное применение данного Типа КЭ, так же, как и пятого признака схемы, вызывает необходимость доработки расчётной модели для её корректной работы.

Практическое использование

Признак схемы 1 (две степени свободы в узле, перемещения X, Z) XOZ

При выполнении расчёта плоской металлической фермы из металлических уголков целесообразно применять признак схемы 1 (Две степени свободы в узле), а стержневым элементам назначать Тип КЭ 1.
Чтобы назначить КЭ тип 1 элементам схемы, следует отметить нужные элементы и вызвать команду смена типа КЭ (см. статью https://rflira.ru/kb/3/488/)

Признак_схемы_1.png

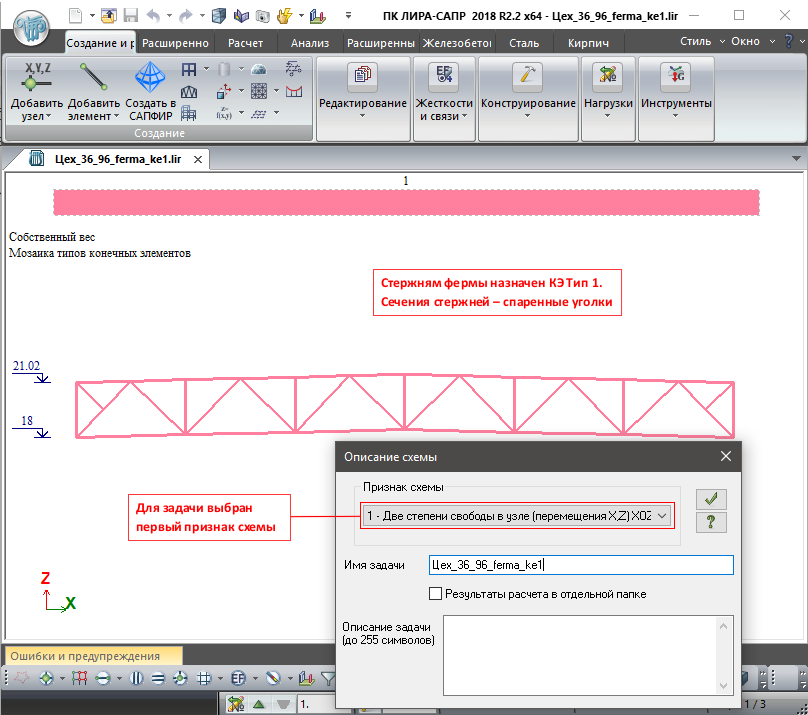
Ферма из спаренных уголков

По умолчанию ЛИРА назначает вновь создаваемым стержням КЭ тип 10 – универсальный пространственный стержневой КЭ, обладающий шестью степенями свободы в узле. Для корректной работы данного элемента в составе фермы для задачи с пятым признаком схемы, требуется дополнительно выполнить следующие операции:
1 Отметка стержней и установка шарниров на концах;
2 Отображение местных осей стержней для правильного назначения узлов установки шарниров в стержнях

Применение КЭ1 позволит сэкономить время на выполнении вышеуказанных операций и сократит время выполнения расчёта компьютером.

Область применения первого признака схемы:

Плоские шарнирно-стержневые системы;
Однопролётные балки;

Ограничения метода: отсутствует возможность узловой передачи момента, т.к. повороты узлов в данной схеме не предусмотрены. Подходит для задач: балка-стенка, плоская шарнирно-стержневая система.

Признак схемы 2 (три степени свободы в узле, перемещения X, Z, Uy) XOZ

При выполнении расчёта фермы из замкнутых гнуто-сварных профилей по серии 1.263.2-4, а также ферм серии 1.460.3-14 типа «Молодечно», требуется выполнить её расчёт как плоской рамной системы, т.к. в узлах соединения элементов данной фермы будут возникать изгибающие моменты, влияющие на проверку и подбор стального сечения.

Признак_схемы_2.png

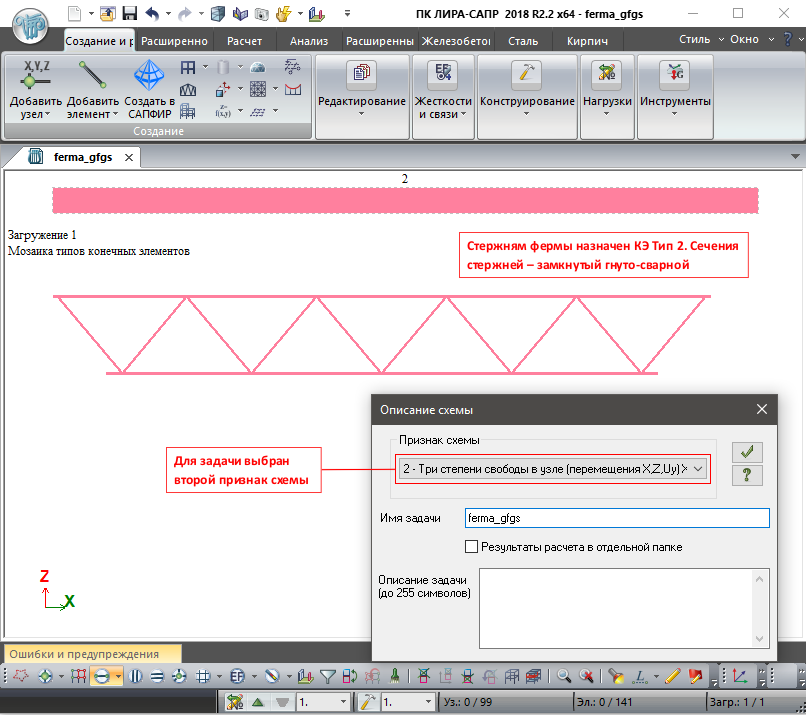
Ферма из замкнутых-гнуто-сварных профилей (прямоугольных или квадратных труб)

Применяемый тип конечного элемента для расчёта фермы: Тип 2, Тип 10.

Для каждого из этих типов КЭ нет необходимости установки шарниров, так что операцию по смене типа КЭ выполнять необязательно.

Область применения второго признака схемы:

Расчёт плоских рам
Расчёт неразрезных многопролётных балок

Ограничения метода: работа в плоскости XOZ

Признак схемы 3 (три степени свободы в узле, перемещения Z, Ux, Uy) XOY

При выполнении расчёта плит, расположенных в горизонтальной плоскости, целесообразно применять признак схемы 3 (три степени свободы в узле), элементам пластин при этом следует назначить тип КЭ11.

Важно: конструктивная схема плиты должна исключать возможность появления в ней мембранных усилий (сил в плоскости самой плиты)

Признак_схемы_3.png

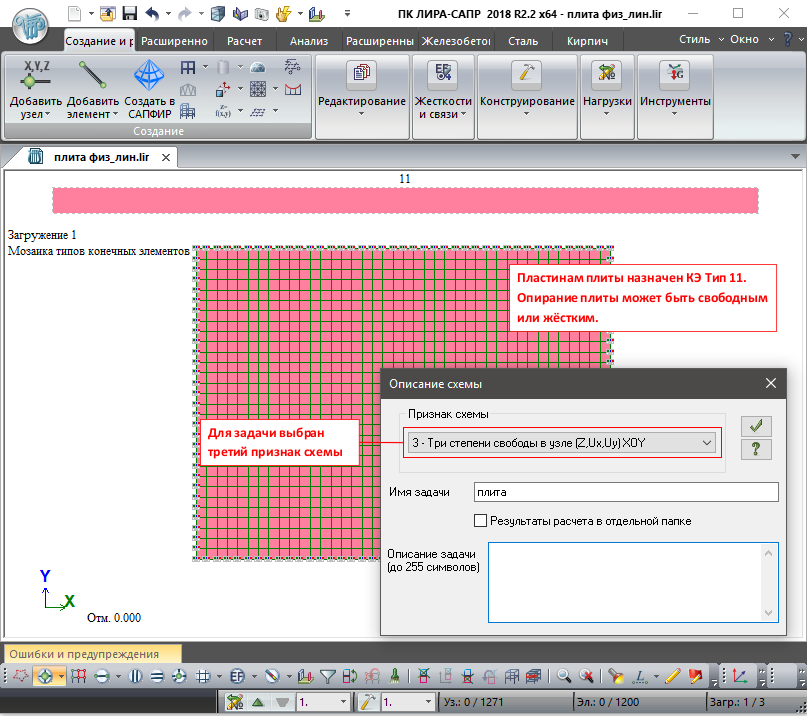
Плита в горизонтальной плоскости

Применение КЭ11 позволит сэкономить время при выполнении расчёта компьютером.

Область применения данного признака схемы:

расчёт неразрезных многопролётных балок
расчёт плитных конструкций со свободным опиранием и жёстким защемлением

Ограничения метода: работа в горизонтальной плоскости (XOY)

Признак схемы 4 (три степени свободы в узле, перемещения X, Y, Z)

При выполнении расчёта пространственной шарнирно-стержневой конструкции, целесообразно применять данный признак схемы. К таким конструкциям, как правило, относятся металлические башни с шарнирным соединением стержней. Рекомендации по расчёту металлических башен можно посмотреть здесь https://rflira.ru/kb/105/722/

Признак_схемы_4.png

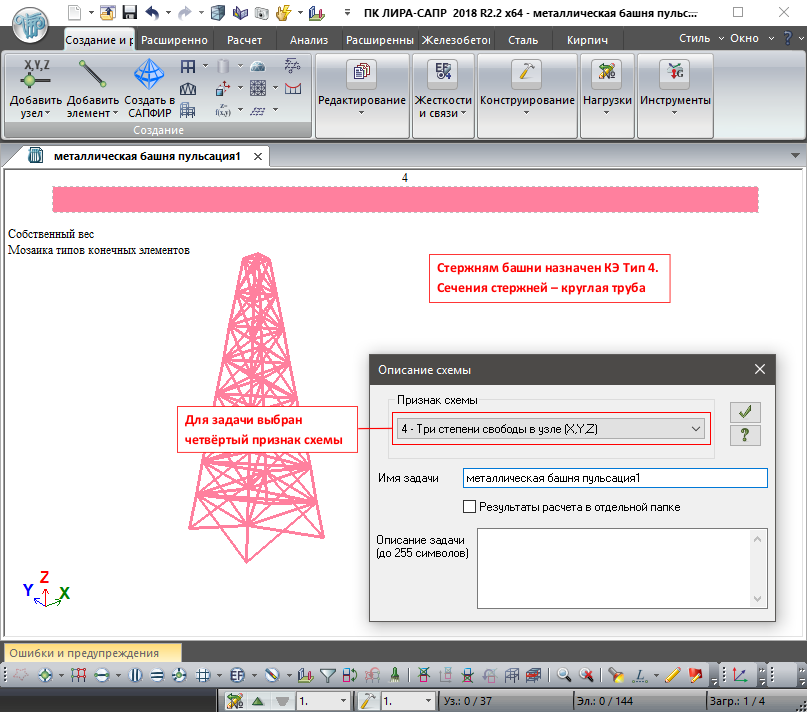
Металлическая башня из круглых труб

Применяемый тип конечного элемента – Тип 4, Тип 10

Выгоды применения данного признака схемы такие же, как у признака 1 – нет необходимости врезки шарниров. Ввиду отсутствия поворотов узлов, тип КЭ менять не обязательно

Область применения четвёртого признака схемы: Шарнирно-стержневые модели

Ограничения метода: нет возможности расчёта пространственных рам, с передачей моментов в узлах схемы.

Признак схемы 5 (шесть степеней свободы в узле, перемещения X, Y, Z, Ux, Uy, Uz)

Это самый широко используемый признак схемы, подходящий для решения подавляющего большинства задач. При моделировании шарнирно-стержневых систем, рекомендуется использовать признак схемы 4, однако, в случае невозможности применения данного признака схемы, когда, к примеру, шарнирно-стержневая модель находится в составе пространственной рамы, используется пятый признак схемы.

Для исключения возможности передачи изгибающего момента, на концах стержней следует устанавливать шарниры (см. статью https://rflira.ru/kb/108/667/). Применение конечного элемента Тип 4 позволит сэкономить время на выполнении данной операции.

При моделировании многостержневых систем, в целях экономии времени целесообразно использовать КЭ Тип 4 для элементов, конструктивная схема которых подразумевает работу элемента только при действии осевых сил.

Данный приём позволит сэкономить время на установке шарниров на концах стержней, а также сократит время расчёта такой схемы компьютером.

Признак_схемы_5.png

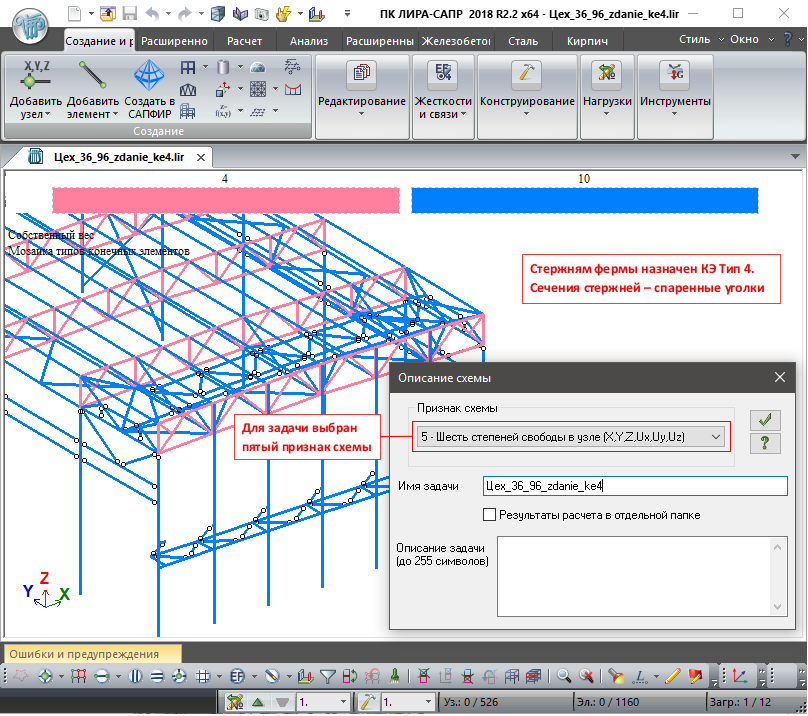
Расчётная модель одноэтажного промышленного здания

Ограничения применения КЭ Тип 4 в пятом признаке схемы: При расчёте на действие динамических нагрузок, подразумевающих определение форм и вычисление периодов/частот колебаний системы, не допускается собирать массы для динамики из нагрузок (в т.ч. собственного веса) стержней КЭ Тип 4, в противном случае будет получена геометрически изменяемая система.

Источник

Пользователь

Сообщений: 155Баллов: 1008Регистрация: 03.08.2015

Таблица 1

№ п/п	Наименование теории прочности	Формула	Геометрическая интерпретация	Примечания
1	2	3	4	5
1	Наибольших главных напряжений	Куб с центром, смещенным относительно начала координат в сторону гидростатического давления	Исторически первая теория прочности – предложенная Г.Галилеем. Удовлетворительно описывает предельное состояние весьма хрупких, достаточно однородных материалов, таких как стекло, гипс, некоторые виды керамики
2	Наибольших главных деформаций	Равносторонний косоугольный параллелепипед с осью симметрии, равнонаклоненной к координатным осям	Предложена Э. Мариоттом и развита Б. Сен-Венаном. Ввиду малой достоверности в настоящее время почти не применяется
3	Наибольших касательных напряжений	Правильная шестигранная призма, равно наклоненная к осям координат	Предложена Ш. Кулоном. Удовлетворительно описывает предельное состояние пластичных малоупрочняющихся материалов (отпущенные стали), для которых характерна локализация пластических деформаций
4	Энергетическая	Круговой цилиндр, описанный вокруг призмы, интерпретирующей теорию максимальных касательных напряжений	Предложена М. Губером, Г. Генки, Р. Мизесом. Хорошо описывает предельное состояние широкого класса пластичных материалов (медь, никель, алюминий, углеродистые и хромоникелевые стали)
5	Теория О. Мора	Шестигранная равнонаклоненная к осям пирамида	Применяется для установления предельного состояния достаточно однородных материалов, по разному сопротивляющихся растяжению и сжатию
6	Друккера–рагера	Двуполостной параболоид вращения, равнонаклоненный к осям координат	Удовлетворительно описывает предельное состояние сравнительно пластичных материалов, для которых параметр
7	Писаренко–Лебедева	Коническая поверхность, описанная вокруг пирамиды Мора. В сечении октаэдрической плоскостью – равносторонний криволинейный треугольник	Хорошо описывает предельное состояние широкого класса достаточно однородных конструкционных материалов. При преобразуется в энергетическую теорию. В случае, когда (весьма хрупкие материалы), результаты вычислений практически совпадают с данными расчета по теории наибольших главных напряжений
8	Гениева	—	Хорошо описывает предельное состояние бетона
9	Кулона – Мора	—	Грунт
10	Боткина	—	Грунт

Условные обозначения
— эквивалентное напряжение при растяжении;
— эквивалентное напряжение при сжатии;
— главные напряжения;
— среднее напряжение;
— интенсивность напряжений

– предельные напряжения растяжения и сжатия, для грунтов

— сцепление;
— угол внутреннего трения;

соответствующей заметке

Использованная литература:
1. Писаренко Г. С. Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, В. В. Матвеев. – Киев: Наукова думка, 1988. – 736 с.

Источник