Линейное растяжение гистограммы изображения

Всем привет. Сейчас мы с научным руководителем готовим к изданию монографию, где пытаемся простыми словами рассказать об основах цифровой обработки изображений. В данной статье раскрывается очень простая, но в тоже время очень эффективная методика повышения качества изображений – эквализация гистограмм.

Для простоты начнём рассмотрение с монохромных изображений (т.е. изображений содержащих информацию только о яркости, но не о цвете пикселей). Гистограммой изображения будем называть дискретную функцию H, определённую на множестве значений [0;2bpp], где bpp – количество бит, отводимое для кодирования яркости одного пиксела. Хоть это и не является обязательным, но гистограммы часто нормируют в диапазон [0;1], выполняя деление каждого значения функции H[i] на общее количество пикселов изображения. В Табл. 1 представлены примеры тестовых изображений и гистограмм, построенных на их основе:
Табл. 1. Изображения и их гистограммы

Внимательно изучив соответствующую гистограмму можно сделать некоторые выводы и о самом исходном изображении. Например, гистограммы очень тёмных изображений характеризуются тем, что ненулевые значения гистограммы сконцентрированы около нулевых уровней яркости, а для очень светлых изображений наоборот – все ненулевые значения сконцентрированы в правой части гистограммы.
Интуитивно можно сделать вывод, что наиболее удобным для восприятия человеком будет изображение, у которого гистограмма близка к равномерному распределению. Т.е. для улучшения визуального качества к изображению надо применить такое преобразование, чтобы гистограмма результата содержала все возможные значения яркости и при этом в примерно одинаковом количестве. Такое преобразование называется эквализацией гистограммы и может быть выполнено с помощью кода, приведённого в Листинг 1.
Листинг 1. Реализация процедуры эквализации гистограммы

procedure TCGrayscaleImage.HistogramEqualization;
const
  k = 255;
var
  h: array [0 .. k] of double;
  i, j: word;
begin
  for i := 0 to k do
    h[i] := 0;
  for i := 0 to self.Height — 1 do
    for j := 0 to self.Width — 1 do
      h[round(k * self.Pixels[i, j])] := h[round(k * self.Pixels[i, j])] + 1;
  for i := 0 to k do
    h[i] := h[i] / (self.Height * self.Width);

  for i := 1 to k do
    h[i] := h[i — 1] + h[i];
  for i := 0 to self.Height — 1 do
    for j := 0 to self.Width — 1 do
      self.Pixels[i, j] := h[round(k * self.Pixels[i, j])];
end;

В результате эквализации гистограммы в большинстве случаев существенно расширяется динамический диапазон изображения, что позволяет отобразить ранее не замеченные детали. Особенно сильно этот эффект проявляется на тёмных изображениях, что показано в Табл. 2. Кроме того, стоит отметить ещё одну важную особенность процедуры эквализации: в отличие от большинства фильтров и градационных преобразований, требующих настройки параметров (апертуры и констант градационных преобразований) эквализация гистограммы может выполняться в полностью автоматическом режиме без участия оператора.
Табл. 2. Изображения и их гистограммы после эквализации

Легко можно заметить, что гистограммы после эквализации имеют своеобразные заметные разрывы. Это связано с тем, что динамический диапазон выходного изображения шире диапазона исходного. Очевидно, что в этом случае рассмотренное в Листинг 1 отображение не может обеспечить ненулевые значения во всех карманах гистограммы. Если всё-таки необходимо добиться более естественного вида выходной гистограммы, можно использовать случайное распределение значений i-ого кармана гистограммы в некоторой его окрестности.
Очевидно, что эквализация гистограмм позволяет легко повышать качество монохромных изображений. Естественно хочется применить подобный механизм и к цветным изображениям.
Большинство не очень опытных разработчиков представляют изображение в виде трёх цветовых каналов RGB и пытаются применить процедуру эквализации гистограммы к каждому цветовому в отдельности. В некоторых редких случаях это позволяет добиться успеха, но в большинстве случаев результат так себе (цвета получаются неестественными и холодными). Это связано с тем, что модель RGB неточно отображает цветовосприятие человека.
Вспомним о другом цветовом пространстве – HSI. Эта цветовая модель (и другие родственные ей) очень широко используются иллюстраторами и дизайнерам так как позволяют оперировать более привычными для человека понятиями цветового тона, насыщенности и интенсивности.
Если рассмотреть проекцию RGB-куба в направлении диагонали белый-чёрный, то получится шестиугольник, углы которого соответствуют первичным и вторичным цветам, а все серые оттенки (лежащие на диагонали куба) при этом проецируются в центральную точку шестиугольника (см. Рис. 1):

Рис. 1. Проекция цветового куба
Чтобы с помощью этой модели можно было закодировать все цвета, доступные в RGB-модели, необходимо добавить вертикальную ось светлоты (или интенсивности) (I). В итоге получается шестигранный конус (Рис. 2, Рис. 3):

Рис. 2. Пирамида HSI (вершины)
В этой модели цветовой тон (H) задаётся углом относительно оси красного цвета, насыщенность (S) характеризует чистоту цвета (1 означает совершенно чистый цвет, а 0 соответствует оттенку серого). При нулевом значении насыщенности тон не имеет смысла и не определен.

Рис. 3. Пирамида HSI
В Табл. 3 показано разложение изображения по компонентам HSI (белые пикселы в канале тона соответствуют нулевой насыщенности):
Табл. 3. Цветовое пространство HSI

Считается, что для повышения качества цветных изображений наиболее эффективно применять процедуру эквализации к каналу интенсивности. Именно это и продемострировано в Табл. 4
Табл. 4. Эквализация различных цветовых каналов

Надеюсь, этот материал показался вам как минимум интересным, как максимум полезным. Спасибо.

Источник

2.8. Выравнивание гистограмм

Существует три основных метода повышения контраста изображения:

линейная растяжка гистограммы (линейное контрастирование),
нормализация гистограммы,
выравнивание (линеаризация или эквализация, equalization) гистограммы.

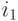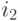Линейная растяжка сводится к присваиванию новых значений интенсивности каждому пикселю изображения. Если интенсивности исходного изображения изменялись в диапазоне от $i_{1}$ до $i_{2}$ , тогда необходимо линейно «растянуть» указанный диапазон так, чтобы значения изменялись от 0 до 255. 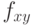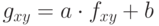Для этого достаточно пересчитать старые значения интенсивности $f_{xy}$ для всех пикселей (x,y) согласно формуле $g_{xy} = a cdot f_{xy} + b$ , где коэффициенты 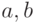a,b просто вычисляются, исходя из того, что граница 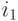$i_{1}$ должна перейти в 0, а 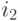$i_{2}$ – в 255.

Нормализация гистограммы в отличие от предыдущего метода обеспечивает растяжку не всего диапазона изменения интенсивностей, а только его наиболее информативной части. Под информативной частью понимается набор пиков гистограммы, т.е. интенсивности, которые чаще остальных встречаются на изображении. Бины, соответствующие редко встречающимся интенсивностям, в процессе нормализации отбрасываются, далее выполняется обычная линейная растяжка получившейся гистограммы.

Выравнивание гистограмм – это один из наиболее распространенных способов. Цель выравнивания состоит в том, чтобы все уровни яркости имели бы одинаковую частоту, а гистограмма соответствовала равномерному закону распределения. Допустим, что задано изображение в оттенках серого, которое имеет разрешение N times M пикселей. Количество уровней квантования яркости пикселей (число бинов) составляет 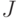. Тогда в среднем на каждый уровень яркости должно выпадать $n_{aver} = frac{N cdot M}{J}$ пикселей. Базовая математика лежит в сопоставлении двух распределений. 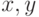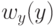Пусть x,y – случайные величины, описывающие изменение интенсивности пикселей на изображениях, $w_{x}(x)$ – плотность распределения интенсивности на исходном изображении, $w_{y}(y)$ – желаемая плотность распределения. Необходимо найти преобразование плотностей распределения 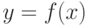y=f(x) , которое позволило бы получить желаемую плотность:

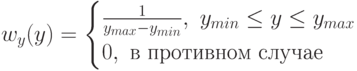
$w_y(y)=begin{cases} frac{1}{y_{max}-y_{min}}, y_{min} le y le y_{max}\ 0, в противном случае\ end{cases}$

Обозначим через 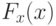$F_{x}(x)$ и $F_{y}(y)$ интегральные законы распределения случайных величин и . Из условия вероятностной эквивалентности следует, что $F_{x}(x)=F_{y}(y)$ . Распишем интегральный закон распределения по определению:

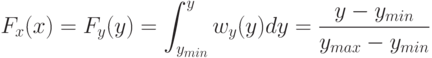
$F_{x}(x)=F_{y}(y) = int_{y_{min}}^{y}{w_{y}(y)dy = frac{y-y_{min}}{y_{max}-y_{min}}}$

Отсюда получаем, что

$y=(y_{max}-y_{min})F_{x}(x)+y_{min}$

Осталось выяснить, как оценить интегральный закон распределения 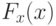$F_{x}(x)$ . Для этого необходимо сначала построить гистограмму исходного изображения, затем нормализовать полученную гистограмму, разделив величину каждого бина на общее количество пикселей 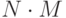N cdot M . Значения бинов можно рассматривать как приближенное значение функции плотности распределения $w_{x}^{*}(x),0leq x leq 255.$ . Таким образом, значение интегральной функции распределения можно представить как сумму следующего вида:

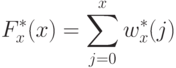
$F_{x}^{*}(x) = sum_{j=0}^{x}{w_{x}^{*}(j)}$

Построенную оценку можно использовать для вычисления новых значений интенсивности. Заметим, что перечисленные преобразования гистограмм можно применять не только ко всему изображению, но и к отдельным его частям.

В библиотеке OpenCV реализована функция equalizeHist, которая обеспечивает повышение контрастности изображения посредством выравнивания гистограммы [1, 7]. Прототип функции показан ниже.

void equalizeHist(const Mat& src, Mat& dst)

Функция работает в четыре этапа:

Вычисление гистограммы исходного изображения src. Отметим, что src – 8-битное одноканальное изображение.
Нормализация гистограммы. Нормализация посредством деления величины каждого бина гистограммы на общее количество пикселей.
Построение интегральной гистограммы $H_{i}' = sum_{0 leq j < H_{j}$ .
Определение нового значения интенсивности пикселя dst(x,y) = H'(src(x,y)).

Далее приведем пример программы, обеспечивающей выравнивание гистограммы. Приложение принимает в качестве аргумента командной строки название исходного изображения. После выполнения операции выравнивания гистограммы выполняется отображение исходного изображения1, переведенного в оттенки серого (рис. 7.11, слева), и изображения с выровненной гистограммой (рис. 7.11, справа).

#include <stdio.h>
#include <opencv2/opencv.hpp>

using namespace cv;

const char helper[] =
«Sample_equalizeHist.exe <img_file>n
t<img_file> — image file namen»;

int main(int argc, char* argv[])
{
const char *initialWinName = «Initial Image»,
*equalizedWinName = «Equalized Image»;
Mat img, grayImg, equalizedImg;
if (argc < 2)
{
printf(«%s», helper);
return 1;
}
// загрузка изображения
img = imread(argv[1], 1);
// преобразование в оттенки серого
cvtColor(img, grayImg, CV_RGB2GRAY);
// выравнивание гистограммы
equalizeHist(grayImg, equalizedImg);

// отображение исходного изображения и гистограмм
namedWindow(initialWinName, CV_WINDOW_AUTOSIZE);
namedWindow(equalizedWinName, CV_WINDOW_AUTOSIZE);
imshow(initialWinName, grayImg);
imshow(equalizedWinName, equalizedImg);
waitKey();

// закрытие окон
destroyAllWindows();
// осовобождение памяти
img.release();
grayImg.release();
equalizedImg.release();
return 0;
}

Результат выравнивания гистограммы

Рис.
7.11.
Результат выравнивания гистограммы

Источник

В этой статье мы расскажем вам о том, как можно своими руками реализовать один из методов улучшения качества изображений с помощью усиления контраста отдельных областей. Данный метод называется эквализацией (выравниванием) гистограммы и его реализацию мы покажем далее.

Эквализация гистограммы — это один самых простых методов улучшения качества изображения, однако, в литературе и интернете сложно найти пример какой-либо простой реализации без погружения в смутные детали. Эквализация, это просто процедура выравнивания гистограммы изображения, путем воздействия (т.е. коррекции) яркости отдельных пикселей.

Дело в том, что гистограмма произвольного изображения представляет собой график, отображающий в виде пиков, количество пикселей в изображении с определенной яркостью, и, как правило, для некоторого изображения она представляет собой множество пиков неравномерно распределенных по графику.

Неравномерное распределение, в данном случае, означает что в гистограмме есть области в которых сосредоточена большая часть пиков или наоборот меньшая, т.е. в пространстве графика присутствуют участки, где плотность значений выше/ниже, чем в среднем по графику. Процедура эквализации сделает распределение значений в гистограмме более равномерным, а это значит что в ней почти не останется пропусков и областей с чрезмерно высоким количеством (и высотой) пиков.

Возможно, подробное объяснение непонятно, однако, я предлагаю вам взглянуть на код примера, сделанный с использованием библиотеки ppmformats:

import std.conv;
import std.stdio;

import ppmformats;

auto histogram(PixMapFile pmf)
{
float[256] histogram = 0;

foreach (e; pmf.array)
{
auto I = cast(int) e.luminance;
histogram[I]++;
}

return histogram;
}

auto equalize(PixMapFile pmf)
{
import std.algorithm : filter, map, min, reduce, sum;
import std.range : iota;

auto histogram = pmf.histogram;

auto cdf(float x)
{
return histogram[0..x.to!int].sum;
}
auto m = iota(0, 256)
.map!(a => cdf(a))
.filter!(a => (a > 0))
.reduce!min;
auto S = pmf.width * pmf.height;

foreach (i,e; pmf.array)
{
auto I = e.luminance;
auto X = cdf(I);
float L = ((X — m) / (S — 1)) * 255;
float NI = L / I;
pmf[i] = e * NI;
}
}

auto histogramToPPM(PixMapFile pmf, int width = 256, int height = 128)
{
import std.algorithm : map;
import std.range : array;

auto S = pmf.width * pmf.height;
auto hist = pmf
.histogram[]
.map!(a => a / S)
.array;

auto img = new P6Image(width, height, new RGBColor(255, 255, 255));
foreach (i, e; hist)
{
auto H = cast(int) (100 * e * (height >> 2));
foreach (j; 0..H)
{
img[i, height-j] = new RGBColor(0,0,0);
}
}
return img;
}

void main()
{
auto pmf = new P6Image;
pmf.load(`/home/aquareji/D/Lenna.ppm`);
pmf.histogramToPPM.save(`Lenna_before.ppm`);
pmf.equalize;
pmf.histogramToPPM.save(`Lenna_after.ppm`);
pmf.save(`/home/aquareji/D/Lenna_equalize.ppm`);
}

Результат применения скрипта к уже всем приевшемуся изображению Лены:

Линейное растяжение гистограммы изображения

А вот оригинальное изображение для сравнения:

Линейное растяжение гистограммы изображения

Спросите, а причем тут гистограмма?

Для ответа на этот вопрос была создана вспомогательная функция histogramToPPM, которая генерирует из некоторого изображения рисунок его гистограммы (в виде PPM P6) и позволит увидеть разницу между двумя изображениями. До процедуры эквализации в изображении, содержащем график яркостей (т.е. гистограмму) будут присутствовать множественные разрывы и большие области, в которых сосредоточена большая часть ярких участков изображения, вот гистограмма оригинального изображения:

Линейное растяжение гистограммы изображения

А вот для сравнения выровненная гистограмма, которая получена после процедуры эквализации:

Линейное растяжение гистограммы изображения

Видно, что график стал более равномерным, а локальные области максимальной плотности ярких участков исчезли и гистограмма стала более равномерной. В свою очередь, это привело к тому, что контраст некоторых областей стал сильнее и динамический диапазон изображения стал более насыщенным, а это означает, что качество изображения стало несколько выше.

Теперь давайте приступим к разбору реализации алгоритма эквализации. Прежде всего, большое спасибо автору статьи о реализации данного алгоритма на F#. Объяснения этого автора оказались очень качественными, а некоторые идеи мы применили в своей реализации алгоритма.

Но, возвращаемся к коду.

Процедура equalize использует функцию histogram, которая возвращает массив float с фиксированной размерностью (а, именно — 256, поскольку яркости пикселей находятся в диапазоне от 0 до 255, и их всего 256) и принимает в качестве аргумента универсальный тип изображений в ppmformats под названием PixMapFile. Функция histogram в самом начале своей работы присваивает всем элементам одноименного массива 0 (поскольку иначе не сработает дальнейшая схема подсчета яркостей), а затем проходит по всем пикселям изображения, вычисляет яркость каждого, приводит к int и использует приведенное значение в качестве индекса массива, увеличивая таким образом значение в массиве яркостей на 1. Весь цикл при этом приведет к тому, что из-за ограниченности целого значения яркостей, каждый пиксель внесет свое значение яркости в копилку массива гистограммы.

Примечание автора. Если вначале функции histogram не присвоить 0 фиксированному массиву с тем же именем, то он будет инициализирован значением float.nan, и прибавление каждый раз 1 к этом значению приведет к тому, что весь массив окажется заполнен только значениями float.nan. За подробными объяснениями почему это так, лучше обратиться к спецификации IEEE 754 относительно формата float.

Процедура equalize сначала получает гистограмму и сохраняет ее в переменную histogram.

Примечание автора. Обращаем ваше внимание на то, что здесь точно также как и в функции histogram, в качестве типа входного аргумента использован тип PixMapFile и, соответственно, процедура не возвращает никакого значения, а лишь модифицирует входной аргумент.

Эта переменная нужна для того, чтобы рассчитать функцию распределения для изображения, которая для некоторой яркости I представляет собой сумму всех яркостей в гистограмме histogram от нулевой до I. Соответственно, вычисление функции распределения реализовано по указанной схеме с помощью внутренней функции cdf, принимающей в качестве аргумента некоторую яркость x, приводимую к int. Процедура sum, использованная для суммирования всего среза в cdf, взята из std.algorithm, как указано в импортах.

После определения функции распределения необходимо вычислить ее минимально возможное значение отличное от нуля. Для этого была определена переменная m, в которую помещается вычисленное значение ненулевого минимума.

Само вычисление реализовано следующим образом: поскольку область определения функции распределения лежит в интервале от 0 до 256 (не включая последнее значение), то с помощью iota генерируется весь диапазон входных значений, к которому далее применяется map совместно с cdf (это обеспечивает генерацию всех возможных значений cdf). Данный диапазон значений фильтруется с помощью filter на предмет ненулевых значений и таким образом избавленный от нулей поступает на вход функции reduce c шаблонным параметром в виде функции min, находящей минимум для двух значений. Поскольку reduce реализует поэлементную свертку диапазона (в данном случае, попарную) с помощью некоторой функции, то применение min здесь дает минимальное значение из всей выборки, и именно оно сохраняется в переменную m.

Дальнейшая часть алгоритма предельно простая и для ее работы необходима переменная S, которая содержит количество всех пикселей в изображении (длина, умноженная на ширину). После вычисления площади изображения, необходимо скорректировать яркость каждого пикселя в отдельности для чего вычисляется его яркость I, значение функции распределения для данной яркости X, а также новая яркость L, вычисление которой представляет реализацию формулы из статьи с HabrHabr, так сказать, «в лоб».

На вычислении трех этих значений сходство с упоминающейся статьей заканчивается, и начинается зыбкая область смутных догадок: для коррекции пикселя потребуется вычислить во сколько раз отличаются его новая (L) и исходная яркости (I) и соответственно увеличить в это количество яркость текущего пикселя, что реализовано банальным умножением пикселя на получившийся коэффициент коррекции (NI).

Примечание автора. Данная идея работает отчасти потому, что умножение/деление пикселя на некое число приводит к изменению его яркости: умножение ее увеличивает, а деление — уменьшает. Однако, мы используем умножение, т.к. значение NI большее 1 эквивалентно увеличению яркости (работает так, будто у нас обычное умножение с повышением яркости), а меньшее 1 — делению (обычный математический факт для чисел).

Теперь, мы перейдем к описанию вспомогательной функции histogramToPPm, которая принимает в качестве аргументов общий тип изображений PixMapFile, длину и ширину графического представления гистограммы, которое будет представлено типом P6Image.

Сначала, мы рассчитываем площадь изображения (т.е. общее количество в нем точек-пикселей), затем получаем и несколько обрабатываем гистограмму для того, чтобы вместо количества точек с конкретной яркостью, у нас было процентное отношение количества точек с данной яркостью ко всему изображению: для этого используется map с обычным делением значения на общее количество точек и array, для превращение диапазона в обычный массив.

Примечание автора. Здесь применен небольшой лайфхак, про который вам нигде и никогда не расскажут. Заключается он в том, что к функции, дающей некоторый массив (особенно это касается массивов с фиксированной размерностью) добавлены квадратные скобки, говорящие о том, что берется срез размером с весь массив и его тип — массив того же типа, что и был, но уже с динамической размерностью! Дело в том, что некоторые функции стандартной библиотеки не любят разного рода массивы и предпочитают вместо них диапазоны, а срез, по мнению D, также является входным диапазоном. Таким образом, если вдруг функция из стандартной библиотеки не принимает массив, то просто добавьте квадратные скобки после аргумента — и все будет как надо.

После предварительной подготовки массива-гистограммы, создается новое изображение формата P6 с длиной width, шириной height и в качестве заполнителя используется белый цвет (по умолчанию, в ppmformats используется черный). С полученным изображением производиться отрисовка столбцов гистограммы, для чего происходит проход по всем значениям гистограммы: с помощью текущего ее значения e вычисляется высота столбца H для отрисовки пиков гистограммы.

Высота H считается из того факта, что значения в массиве представлены процентным отношением, выраженном в долях единицы, и предположения о том, что высота занимает какой-то процент от половины ширины изображения (половина выражена сдвигом на 2, что позволяет избавиться от операции деления). Внутренний цикл с переменной j выполняет отрисовку отдельного столбца, просто заполняя пиксели, соответствующие высоте H на картинке черным цветом, рисуя тем самым одну черную линию. Таким образом и получается отрисовка всех столбцов гистограммы.

Примечание редактора. Хотя длина и ширина изображения гистограммы настраиваются, но все же лучше будет, если длина гистограммы останется равной 256 (по количеству возможных яркостей). Кроме того, лишний раз напоминаем о том, что вам потребуется сменить пути в примере, если захотите тестировать пример на своих файлах.

Ради интереса (а также для того, чтобы поместить результирующее изображение и графики гистограмм в статью), мы переписали пример с использованием dlib вместо ppmformats:

#!/usr/bin/env dub
/+ dub.sdl:
name «exp»
dependency «dlib» version=»~>0.17.0″
+/
//

import dlib.image;

auto histogram(SuperImage simg)
{
float[256] histogram = 0;

foreach (i; 0..simg.width)
{
foreach (j; 0..simg.height)
{
auto I = cast(int) (simg[i, j].luminance * 255.0);
histogram[I]++;
}
}

return histogram;
}

auto histogramToPNG(SuperImage simg, int width = 256, int height = 128)
{
import std.algorithm : map;
import std.range : array;

auto S = simg.width * simg.height;
auto hist = simg
.histogram[]
.map!(a => a / S)
.array;

auto img = image(width, height);
foreach (i; 0..width)
{
foreach (j; 0..height)
{
img[i, j] = Color4f(1.0f, 1.0f, 1.0f);
}
}

foreach (i, e; hist)
{
auto H = cast(int) (100 * e * (height >> 2));
foreach (j; 0..H)
{
img[cast(int) i, height-j] = Color4f(0.0f, 0.0f, 0.0f);
}
}
return img;
}

auto equalize(SuperImage simg)
{
import std.algorithm : filter, map, min, reduce, sum;
import std.conv : to;
import std.range : iota;

auto histogram = simg.histogram;

auto cdf(float x)
{
return histogram[0..x.to!int].sum;
}
auto m = iota(0, 256)
.map!(a => cdf(a))
.filter!(a => (a > 0))
.reduce!min;
auto S = simg.width * simg.height;

foreach (i; 0..simg.width)
{
foreach (j; 0..simg.height)
{
auto I = simg[i, j].luminance;
auto X = cdf(I * 255);
float L = ((X — m) / (S — 1));
float NI = L / I;
simg[i, j] = simg[i, j] * NI;
}
}
}

void main()
{
auto img = load(`/home/aquareji/Downloads/Lenna.png`);
img.histogramToPNG.savePNG(`Lenna_before.png`);
img.equalize;
img.histogramToPNG.save(`Lenna_after.png`);
img.savePNG(`Lenna_equalized.png`);
}

Как видите, код почти такой же, за исключением пары моментов: в функции получения гистограмм histogram, а также внутри функции equalize получаемые значения из luminance умножаются на 255 (поскольку, в dlib яркость может принимать значения от 0.0f до 1.0f); функция histogramToPPM заменена на аналог histogramToPNG, а тип цвета сменился с RGBColor на Color4f. Кроме того, в предыдущем случае, мы запускали приложение с помощью rdmd (при этом неявно предполагается, что файл примера находиться в той же папке, что и файл ppmformats.d, взятый с гитхаба разработчика), но в этом случае используется dub с аргументом —single в опции run, как описывалось в одной из наших статей.

В заключение остается только сказать, что теперь в ваших руках оказался один из инструментов улучшения изображений и мы от имени блога LightHouse Software желаем вам успеха в использовании и улучшении данного инструмента.

Источник