Энергия упругой деформации растяжения

Любое
упруго деформированное тело обладает
потенциальной энергией,
так как
изменяется взаимное расположение
отдельных частей тела. Рассмотрим случай
растяжения пружины.
Растяжение
будем производить очень медленно, чтобы
силу
![]() ,
,
с которой мы действуем на пружину, можно
было считать все время равной по модулю
упругой силе![]() .
.
Тогда![]() гдек, х –
гдек, х –
соответственно жесткость и удлинение
пружины. Тогда работа, которую нужно
совершить, чтобы вызвать удлинение (или
сокращение) х
пружины,
равна
![]() (8.12)
(8.12)
Эта
работа идет на увеличение потенциальной
энергии пружины. Следовательно,
зависимость потенциальной энергии
пружины от удлинения х
имеет вид
![]() ,(8.13)
,(8.13)
если
считать, что потенциальная энергия
недеформированной пружины равна нулю.
Потенциальная энергия упруго деформированного стержня равна
![]() ,
,
(8.14)
где
![]() –
–
объем стержня.
Отношение
энергии
![]() к тому объему
к тому объему![]() ,
,
в котором она заключена, называетсяплотностью
энергии u.
Тогда
![]()
– плотность энергии упругой деформации
при растяжении (или сжатии).
Аналогично
нетрудно получить, что плотность энергии
деформации при сдвиге равна
![]() .
.
6. Кручение
Деформации
кручения и изгиба являются деформациями
неоднородными. Это значит, что в этих
случаях деформации внутри тела меняются
от точки к точке.
Возьмем
однородную проволоку, верхний конец ее
закрепим, а к нижнему концу приложим
закручивающие силы. Они создадут
вращающий момент относительно продольной
оси проволоки. При этом каждый радиус
нижнего основания повернется вокруг
продольной оси на угол
![]() .
.
Такая деформация называется кручением.
Закон Гука для деформации кручения
имеет вид
![]() , (8.15)
, (8.15)
где
![]() – модуль кручения, постоянная для данной
– модуль кручения, постоянная для данной
проволоки. Модуль кручения зависит не
только от материала, но и от геометрических
размеров проволоки.
Выведем
выражение для модуля кручения.
Пусть
имеется цилиндрическая трубка радиуса
![]() .
.
Причем толщина ее![]() очень
очень
мала по сравнению с радиусом. Площадь
сечения трубки равна
![]() .
.
Обозначим через![]() касательное напряжение в том же основании.
касательное напряжение в том же основании.
Тогда момент сил, действующий на это
основание, будет![]() .
.
При закручивании совершается работа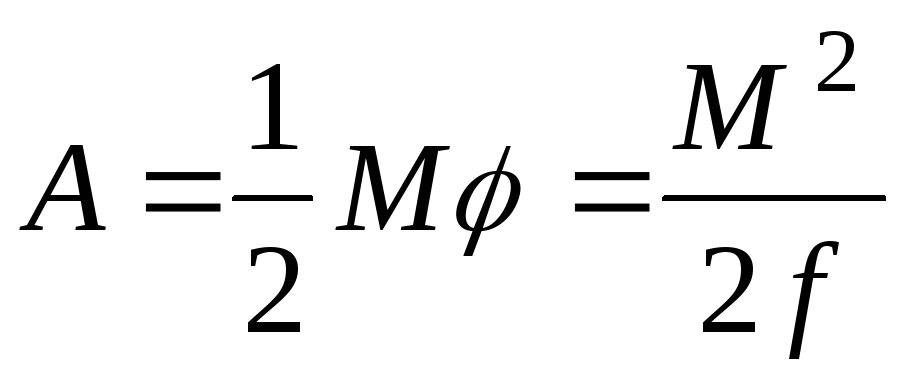 .
.
Разделим
ее на объем трубки
![]() .
.
Найдем плотность упругой энергии при
деформации кручения
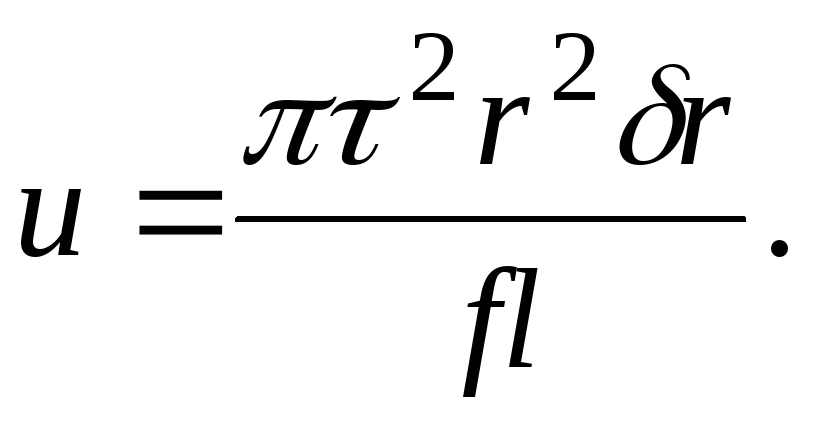 (8.16)
(8.16)
Найдем
эту же величину иначе.
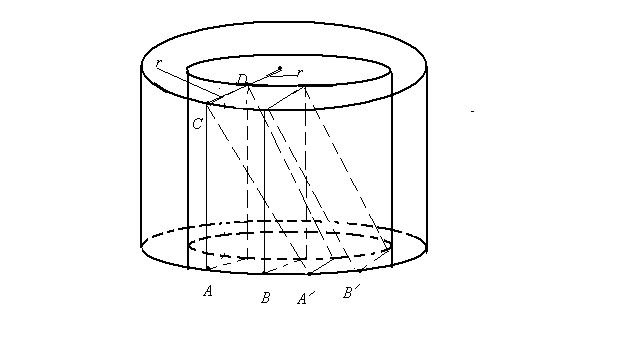
Мысленно
вырежем из трубки бесконечно короткую
часть (рис.8.5).
| Рис. |
В
результате кручения бесконечно малый
элемент трубки ABDC
перейдет в положение
![]() .
.
Это есть сдвиг. Таким образом, деформацию
кручения можно рассматривать как
неоднородный сдвиг. Плотность упругой
энергии при сдвиге равна
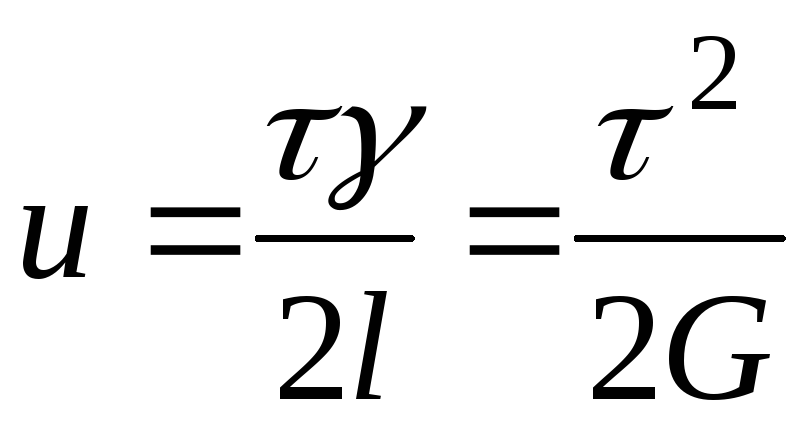 (8.17)
(8.17)
Приравнивая
его выражению (8.16), находим искомое
соотношение
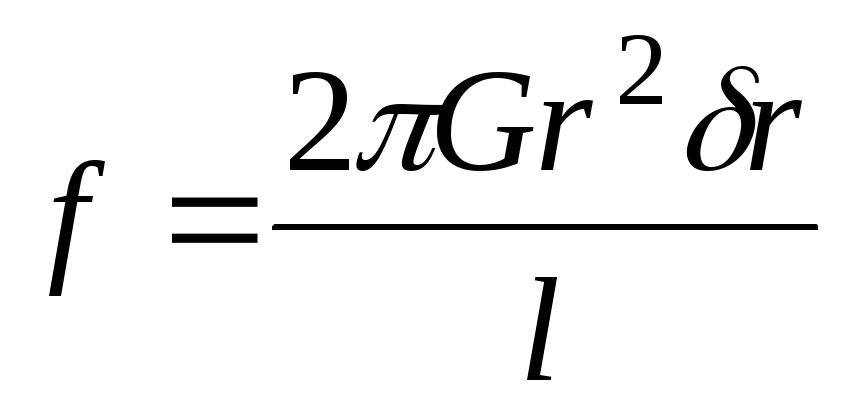 (8.18)
(8.18)
Если
стенка трубки имеет конечную толщину,
то модуль
![]() найдется интегрированием последнего
найдется интегрированием последнего
выражения по![]() .
.
Это дает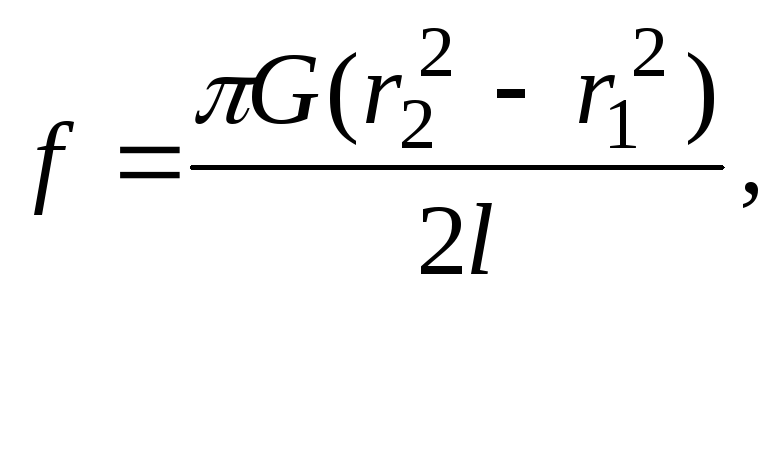 где
где
![]() – внутренний радиус трубки,
– внутренний радиус трубки,![]() – внешний радиус трубки.
– внешний радиус трубки.
Для
сплошной проволоки радиуса
![]() модуль
модуль
кручения .
Контрольные вопросы
Что
называется деформацией? Какие деформации
называются упругими? Приведите примеры
упругих деформаций.Какова физическая
сущность упругих сил?Сформулируйте
закон Гука? Когда он справедлив?Дайте
объяснение качественной диаграмме
напряжений. Что такое предел
пропорциональности, упругости и
прочности?Что такое упругий
гистерезис и упругое последействие?Каков физический
смысл модуля Юнга и модуля сдвига?Что такое упругое
последействие?Выведите выражения
для деформаций при всестороннем
растяжении.Что называется
коэффициентом Пуассона?Определите энергию
деформированного тела.Что называется
плотностью упругой энергии? Получите
формулы этой энергии при растяжении и
сдвиге.Какой вид имеет
закон Гука при кручении.Выведите выражение
для модуля кручения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Считая процесс нагружения квазистатическим и учитывая линейную связь Al(N), для потенциальной энергии деформации имеем
Если брус неоднородный, то
Удельная потенциальная энергия деформации, соответственно, равна
Статически неопределимые системы. Перемещение систем в пространстве ограничено связями. Если число связей, наложенных на систему, больше, чем необходимое для ее решения число уравнений статики, то такие системы называют статически неопределимыми. Для их решения используют дополнительные уравнения совместности деформаций. Характерной особенностью статически неопределимых систем является возникновение в них температурных напряжений, образующихся без внешних усилий под воздействием температуры.
При испытании на растяжение обеспечивается однородность напряженного состояния всех точек образца на рабочей длине. Испытание на растяжение достаточно просто, а его результаты в меньшой степени зависят от формы и размеров образца, чем испытания других видов. Наконец, испытание на растяжение позволяет получить достоверные характеристики прочности, упругости и пластичности материала, которые можно также использовать в расчетах деталей, работающих в условиях сложного напряженного состояния.
Характерный вид диаграммы растяжения образца из пластичного материала представлен на рис. 14.3. На этой диаграмме можно выделить четыре основных участка (зоны).
Рис. 143. Диаграммы растяжения образцов
На участке ОЛ материал подчиняется закону Гука. Деформации образца очень малы и при разгрузке исчезают. Участок ОЛ называют зоной упругости. За пределами этого участка деформация образца складывается из упругой и пластической (остаточной) составляющих.
Участок ВС характеризуется нарастанием пластической деформации без увеличения осевой нагрузки (Р = Рт) и называется зоной общей текучести. При нагрузке Рт во всем объеме рабочей части образца происходят необратимые деформации сдвига между кристаллическими слоями. В результате текучести происходит перестройка кристаллической решетки, несущая способность образца увеличивается и для его дальнейшего деформирования требуется повышение нагрузки.
Участок CD называют зоной упрочнения. Здесь удлинение образца сопровождается возрастанием нагрузки, но гораздо более медленным, чем на участке ОЛ. В точке D диаграммы осевая растягивающая нагрузка достигает максимального значения (Р = Ртах). К этому моменту на образце наметилось место будущего разрыва — образовалось местное сужение, называемое шейкой (или пластический шарнир).
Дальнейший ход испытания связан с прогрессирующим утонением шейки и сосредоточением деформации образца в районе шейки. Участок DFдиаграммы носит название зоны местной текучести. Здесь нагрузка плавно уменьшается (Р тах) вплоть до разрушения образца в шейке.
Если образец нагрузить до точки L диаграммы, а затем плавно уменьшить нагрузку, то зависимость между силой и деформацией изобразится отрезком LM, параллельным прямой О А При полной разгрузке образца его удлинение уменьшится, но не исчезнет. Таким образом, полное удлинение образца в точке L складывается из двух составляющих — упругой А/у и остаточной — Д/(кт. При повторном нагружении такого образца материал будет деформироваться упруго до точки L (см. рис. 14.3, б). В результате предварительной вытяжки материал приобрел способность воспринимать без остаточных деформаций большие нагрузки. Исчезла площадка текучести, материал стал более хрупким. Подобное явление, называемое наклепом (или нагартовкой), широко используют в технике.
Параметры диаграммы растяжения в координатах А/—Р зависят не только от свойств материала образца, но и от его размеров. Чтобы получить характеристики материала, машинную диаграмму А/—Р перестраивают в координатах е —а (относительная деформация — напряжение). Связь между координатами определяется зависимостями
где А() — начальная площадь поперечного сечения образца; /() — начальная расчетная длина образца.
Поскольку А0 и /() — константы, диаграмма деформаций при растяжении имеет ту же форму (рис. 14.4, кривая 1). Обработка диаграммы деформаций позволяет определить следующие основные характеристики материала:
- • физический предел текучести от = Рт/Л();
- • предел прочности (временное сопротивление) овр = Ртах/Л0;
• относительное удлинение после разрыва
• относительное сужение после разрыва
Рис. 14.4. Диаграммы деформаций пластичного материала:
1 — условная для испытания на растяжение; 2 — истинная; 3 — условная для испытания
на сжатие
Первые две характеристики относятся к характеристикам прочности, две другие — к характеристикам пластичности. Здесь /к — конечная расчетная длина образца; Ак — площадь поперечного сечения образца в месте его разрыва.
По величине относительного удлинения после разрыва 5 материалы условно разделяют на следующие группы:
- • 8
- • 5%
- • 8 > 15% — пластичные материалы.
Более тщательная обработка диаграммы деформаций при растяжении позволяет определить дополнительные характеристики материала. Предел пропорциональности стм определяют как условное напряжение, при котором отступление от прямой пропорциональной зависимости между нагрузкой и удлинением составляет 50% (рис. 14.5). Для получения величины ап к кривой диаграммы деформаций проводится касательная под углом ап = = arctg(tga/l,5).
Под пределом упругости ау понимается наибольшее напряжение, до которого образец не получает остаточных деформаций. Поскольку определить это значение практически невозможно, условным пределом упругости называют то напряжение, при котором остаточная деформация составляет 0,01% (см. рис. 14.5, б). Для материалов без четко выраженной площадки текучести определяют условный предел текучести а0 2, который соответствует остаточной деформации 0,2% (рис. 14.5, в).
Рис. 14.5. Диаграммы a — е
Следует заметить, что рассмотренная диаграмма деформаций является условной, поскольку в процессе испытания площадь поперечного сечения образца А0 не остается постоянной, а постепенно уменьшается. Напряжение в шейке ак существенно отличается от рассчитанного но формуле a = = Р/А0 Продольная деформация в шейке ?к также значительно превосходит среднюю деформацию образца, характеризуемую величиной 8 (рис. 14.6). Диаграмма зависимости между напряжением и деформацией в шейке носит название истинной диаграммы деформаций (см. рис. 14.4, кривая 2). На участках упругости, текучести и упрочнения она практически совпадает с условной диаграммой деформаций. Последний участок истинной диаграммы деформаций строится как касательная к условной диаграмме,
Рис. 14.6. Характер деформации и эпюра остаточных деформаций в месте разрыва образца пластичного материала
проведенная из точки FK, координаты которой рассчитываются по формулам:
Рис. 14.7. Диаграммы деформации хрупкого материала:
- 1 — при растяжении:
- 2 — при сжатии
Диаграмма деформаций при растяжении образца хрупкого материала не имеет площадки текучести и зоны упрочнения (рис. 14.7). Разрушение образца происходит при наибольшей величине нагрузки (Р = РП1ах) и весьма малой остаточной деформации без образования шейки. Здесь определяется только одна характеристика предела прочности при растяжении ствр = PmJA0.
Испытание на сжатие применяется в основном для определения характеристик малопластичных и хрупких материалов. Его можно рассматривать как обратное испытанию на растяжение (растяжение с обратным знаком).
При малых деформациях пластичные материалы имеют весьма близкие характеристики растяжения и сжатия. Диаграммы деформаций при растяжении и сжатии (в последней напряжения и деформации условно считают положительными) практически совпадают на участках упругости, текучести и упрочнения. Однако по мере нарастания пластических деформаций при сжатии все больше сказывается влияние трения на торнах и увеличение размеров поперечного сечения образца. В результате нагрузка резко возрастает (см. рис. 14.4, кривая 3), а образец сжимается в тонкий диск (рис. 14.8). Пластичный образец довести до разрушения практически не удается — испытание ограничивается силовыми возможностями испытательной машины.
Диаграмма деформаций при сжатии хрупкого образца подобна диаграмме при растяжении (см. рис. 14.7, кривая 2), однако прочность хрупких материалов при сжатии выше, чем при растяжении. Отношение соответству-
Ж 3 и
Рис. 14.8. Испытание на сжатие:
а — сферическая опора нижнего захвата; 6, в — формы выточек на торцах образца; г—е — стадии деформирования пластичного образца; ж—и — характер разрушения хрупкого образца
ющих пределов прочности а]к./а1ф характеризует степень хрупкости материала и составляет:
- • 2,5—3 — для текстолита;
- • 3—5 — для чугунов;
- • 8—14 — для керамики;
- • 12—150 — для вакуумных стекол.
Испытание на сжатие имеет некоторые особенности по сравнению с испытанием на растяжение. Для устранения перекоса образца при непараллель- ности его торцов в одном из захватов испытательной машины предусмотрена установка сферической опоры (см. рис. 14.8, а). Силы трения между торцами образца и плоскими элементами испытательной машины сдерживают поперечную деформацию образца вблизи его торцов.
В результате образец приобретает характерную бочкообразную форму, в его объеме создается сложное неоднородное напряженное состояние, не соответствующее расчетной схеме. Для уменьшения влияния внешнего трения применяют смазки (вазелин, солидол), прокладки (бумага, пропитанная парафином, тефлон), цилиндрические или конические выточки на торцах (рис. 14.8, б, в). Разрушение хрупкого образца при испытании на сжатие происходит вследствие сколов по плоскостям, наклоненным под углом 45° к оси образца (рис. 14.8, ж, з). Если удается устранить влияние сил внешнего трения на образце, при его разрушении возникают продольные трещины (рис. 14.8, и).
Для испытания на растяжение чаще всего используют образцы с цилиндрической рабочей частью (рис. 14.9). Начальный диаметр d0 выбирается из стандартного ряда в пределах d{) = (3 — 25) мм. Начальное значение расчетной длины образца /() = 11,3~ 10d() («длинный» образец) или /() = 5,65~ ~ 5d0 («короткий» образец). Длина цилиндрического участка 1{ > 1,1 /0.
Концы образца оформляются в виде утолщений (головок), форма и размеры которых определяются захватными устройствами испытательной машин. Между рабочей частью и головками предусмотрены переходные уча-
Рис. 14.9. Стандартные образцы для испытания на растяжение:
а, б — цилиндрические; в — плоский
стки, которые служат для уменьшения концентрации напряжений. Для получения характеристик листового материала с толщиной менее 5 мм применяют плоские образцы (см. рис. 14.9, в). Размер s0 равен толщине листа, ширина Ь0 составляет КНЗО мм, расчетная длина /0 =11,3yjs0b0.
Испытание на сжатие проводят на образцах цилиндрической или кубической формы (рис. 14.10). Для предотвращения потери устойчивости цилиндрического образца во время испытания его высота ограничена: А0 = (1-^3)с70
Рис. 14.10. Образцы для испытания на сжатие:
а — цилиндрический; б — кубический
Источник
Для решения сложных задач расчета на прочность успешно применяется энергетический подход, в основе которого лежит определение работы внешних и внутренних сил, определение потенциальной энергии упругой деформации.
Рассмотрим один подход к определению потенциальной энергии упругой деформации.
Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу А на соответствующих перемещениях. Одновременно с этим в упругом теле накапливается потенциальная энергия его деформирования U. При действии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:
А = U + K
При действии статических нагрузок (или если сила прикладывается достаточно медленно, т. е. ее скорость приложения стремится к нулю) К = 0, следовательно,
А = U
Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформации. При разгрузке тела производится работа за счет потенциальной энергии деформации, накопленной телом. То есть, упругое тело является аккумулятором энергии. Это свойство упругого тела широко используется, например, в заводных пружинах часовых механизмов, в луке и т.д. Для вывода необходимых расчетных зависимостей потенциальной энергии деформации рассмотрим простейший случай — растяжение стержня.
На рисунке изображен растягиваемый силой F стержень, удлинение которого соответствует отрезку Δl, а ниже показан график изменения величины удлинения стержня Δl в зависимости от силы F. В соответствии с законом Гука этот график носит линейный характер (стержень растягивается в пределах упругих деформаций).
Пусть некоторому значению силы F соответствует удлинение стержня Δl. Дадим некоторое приращение силе dF. Соответствующее приращение удлинения составит d (Δl ). Тогда элементарная работа на этом приращении удлинения составит:
dA = (F + dF)·d (Δl ) = F·d (Δl ) + dF· d (Δl )
вторым слагаемым, в силу его малости, можно пренебречь, и тогда
dA = F·d (Δl)
Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка — перемещение”, работа внешней силы F на перемещении Δl будет равна площади треугольника ОСВ
A = U = 1/2·F·Δl
Для однородного стержня с постоянным поперечным сечением и при F = const, зная из закона Гука что Δl = FL/EA (здесь и далее_A_ – площадь сечения), получим:
$$ U={1over2} F Delta l = {1over2} F {FLover EA} = {F^2 Lover 2EA}$$
Здесь
U – потенциальная энергия упругой деформации
F – нагрузка
E – Модуль Юнга
L – длина
A – площадь сечения
Для оценки энергоемкости материала используют удельную потенциальную энергию, накапливаемую в единице объема: u= U/V, где V— объем стержня (V=L·A). Зная, что σ=F/A= Eε, для стержня (напряжения σ и деформации ε распределены по объему тела V равномерно) можем записать
$$u={Uover V}= {{{F^2 Lover 2EA}{1over LA}}}
= {sigma^2over 2E}={sigmaepsilonover 2}$$
Потенциальную энергию упругой деформации можем выразить через удельную потенциальную энергию:
$$U=int_{V}udV$$
Связанные статьи
- Теория прочности Мора
- Теории прочности
- Правило знаков
- Концентрация напряжений
- Статически определимые и неопределимые конструкции
- Общие принципы расчета конструкции и условия прочности
- Напряжения
метки: деформация,
потенциальная энергия деформации
Источник
Сопротивление материалов
Деформации при растяжении и сжатии
Продольные деформации при растяжении и сжатии
Характер деформаций, которым подвергается прямой брус при растяжении или сжатии мы определили, проведя опыт с резиновым брусом, на котором была нанесена сетка линий.
Теперь представим себе брус постоянного сечения имеющий длину l, один из концов которого защемлен, а к свободному концу приложена растягивающая сила F. Под действием этой силы брус удлинится на некоторую величину Δl, которую назовем абсолютным удлинением бруса.
Отношение абсолютного удлинения Δl к первоначальной длине бруса l назовем относительным удлинением и обозначим ε:
ε = Δl / l
Относительное удлинение – величина безразмерная, иногда его выражают в процентах.
Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.
***
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой линейной зависимостью, которая называется законом Гука, по имени английского физика Р. Гука (1653-1703 г.г.), установившего этот закон.
Сформулировать закон Гука можно так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.
Математически эта зависимость записывается так:
σ = E ε.
Здесь Е – коэффициент пропорциональности, который характеризует жесткость материала бруса, т. е. его способность сопротивляться деформации; его называют модулем продольной упругости, или модулем упругости первого рода.
Модуль упругости, как и напряжение, выражаются в паскалях (Па).
Значения Е для различных материалов устанавливаются экспериментально-опытным путем, и их величину можно найти в соответствующих справочниках.
Так, для стали Е = (1,96.…2,16) х 105 МПа, для меди Е = (1,00…1,30) х 105 МПа и т. д.
Следует оговориться, что закон Гука справедлив лишь в определенных пределах нагружения.
Если в формулу закона Гука подставить полученные ранее значения относительного удлинения и напряжения: ε = Δl / l , σ = N / А, то можно получить следующую зависимость:
Δl = Nl / (EА).
Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.
Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение ЕА / l называют жесткостью бруса при растяжении и сжатии.
Приведенные выше формулы закона Гука справедливы лишь для брусьев и их участков, имеющих постоянное поперечное сечение, изготовленных из одного материала и при постоянной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами сечения, продольной силой, изменение длины всего бруса определяется, как алгебраическая сумма удлинений или укорочений отдельных участков:
Δl = Σ (Δli)
***
Поперечные деформации при растяжении и сжатии
Описанный ранее опыт с резиновым брусом, на котором нанесена сетка линий, показал, что при растяжении поперечные размеры бруса уменьшаются, а при сжатии – увеличиваются, т. е. брус становится либо тоньше, либо толще. Это явление характерно для брусьев, изготовленных из всех материалов.
Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций для данного материала – величина постоянная.
Впервые на эту зависимость указал французский ученый С. Пуассон (1781-1840 г.г.) и математически она записывается так:
|ε1| = ν |ε|,
где ν – коэффициент поперечной деформации, называемый коэффициентом Пуассона.
Коэффициент Пуассона является безразмерной величиной, и характеризует упругие свойства материала. При растяжении и сжатии этот коэффициент принимается одинаковым.
Значения коэффициента Пуассона для разных материалов установлены опытным путем и их величины можно найти в соответствующих справочниках.
***
Потенциальная энергия деформации при растяжении
При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W.
Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что W = U.
Путем изучения диаграмм растяжения образцов, установлено, что потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна:
U = W = F Δl / 2 = N2 l / (2E А)
Сопротивление материалов оперирует, также, таким понятием, как удельная потенциальная энергия деформации, которая подсчитывается, как потенциальная энергия, приходящаяся на единицу объема бруса.
При одновременном действии растягивающих и сжимающих нагрузок или ступенчатом изменении размеров поперечного сечения бруса, его разбивают на однородные участки и для каждого подсчитывают потенциальную энергию деформации. Потенциальную энергию деформации всего бруса определяют, как сумму потенциальных энергий отдельных участков.
Анализируя формулу потенциальной энергии деформации можно сделать вывод, что эта величина всегда положительная, поскольку в ее выражения входят квадраты линейных и силовых величин. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (поскольку квадрат суммы не равен сумме квадратов слагаемых).
Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж).
***
Материалы раздела «Растяжение и сжатие»:
- Основные понятия о деформации растяжения и сжатия.
- Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.
Смятие
Правильные ответы на вопросы Теста № 5
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 3 | 3 | 1 | 2 | 1 | 3 | 2 | 2 | 1 | 1 |
Источник