Испытание на растяжение является
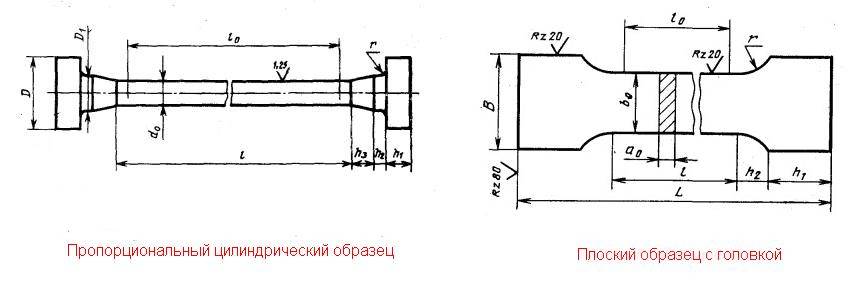
Испытание на растяжение металла заключаются в растяжении образца с построением графика зависимости удлинения образца (Δl) от прилагаемой нагрузки (P), с последующим перестроением этой диаграммы в диаграмму условных напряжений (σ — ε)
Испытания на растяжение проводятся по ГОСТ 1497, по этому же ГОСТу определяются и образцы на которых проводятся испытания.
 Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
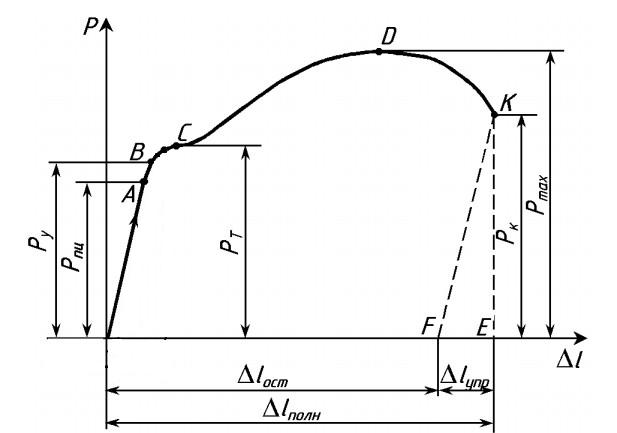
- Участок ОА — участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
- Участок ОВ — участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении
Выше точки В диаграмма растяжения отходит от прямой — деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.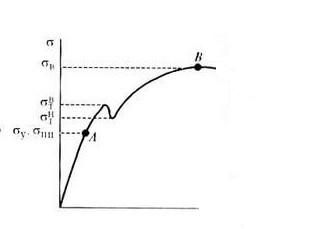 Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение — шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.
Прилагаемая нагрузка для растяжения образца зависит от геометрии этого образца. Чем больше площадь сечения, тем более высокая нагрузка необходима для растяжения образца. По этой причине, получаемая машинная диаграмма не дает качественной оценки механических свойств материала. Чтобы исключить влияние геометрии образца, машинную диаграмму перестраивают в координатах σ − ε путем деления ординат P на первоначальную площадь сечения образца A0 и абсцисс ∆l на lо. Перестроенная таким образом диаграмма называется диаграммой условных напряжений. Уже по этой, новой диаграмме, определяют механические характеристики материала.
Определяются следующие механические характеристики:
Предел пропорциональности σпц – наибольшее напряжение, после которого нарушается справедливость закона Гука σ = Еε , где Е – модуль продольной упругости, или модуль упругости первого рода. При этом Е =σ/ε = tgα , т. е. модуль E это тангенс угла наклона прямолинейной части диаграммы к оси абсцисс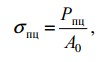
Предел упругости σу — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σу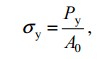
Предел текучести σт – напряжение, при котором происходит увеличение деформации без заметного увеличения растягивающей нагрузки
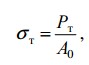 Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести
Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести
Предел прочности (временное сопротивление разрыву) σв – напряжение, соответствующее наибольшей нагрузке Pmax , предшествующей разрыву образца
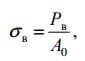
Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности — относительное удлинение δ и относительное сужение ψ
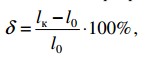
где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца
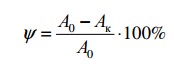

Источник
Испытание на растяжение
Испытание на растяжение — это относительно простой для понимания и объяснения метод испытания материала, и, возможно, его используют чаще остальных. При проведении этого испытания, образец материала растягивают вдоль продольной оси с помощью растягивающего приспособления испытательной машины (Рис. 1.7.4). Испытание проводят с постоянной скоростью, (т.е. с постоянной скоростью растяжения образца), а нагрузку измеряют с помощью датчика нагрузки. Одновременно с этим измеряют удлинение, соответствующее прилагаемой нагрузке. Удлинение можно измерить несколькими способами, в том числе, по пути движения подвижной траверсы, или путем прикрепления к материалу тензодатчика при очень низких величинах деформации.

Рис. 1.7.4. Схема испытания образца для определения прочности на растяжение
Напряжение и соответствующая ему деформация могут быть рассчитаны по приведенным выше формулам. По этим данным можно построить кривую напряжение — деформация, а по этой кривой можно определить ряд свойств. Типичные примеры кривых напряжения-деформации для некоторых материалов представлены на Рис. 1 .7.5.

Рис. 1.7.5. Вид кривых напряжение-деформация для материалов различного типа. Кривые представлены не в масштабе
Примером пластичного или ковкого материала является мягкая сталь, на графике напряжение-деформация для которой показаны: область линейной упругости, четко определяемая точка предела текучести и высокая степень пластичности материала. И, напротив, на графике такого твердого материала, как гипс, видна только линейная область упругости, а затем происходит разрушение без каких-либо признаков пластической деформации.
Многие пластмассы, такие, как полиметилметакрилат, также являются жесткими материалами, однако они обладают меньшей хрупкостью, чем гипс. Поведение эластомера, примером которого является силиконовый оттискной материал, очень необычно по сравнению с другими материалами. Оказывается на графике напряжение-деформация у него отсутствует область линейной упругости, а область упругого восстановления у эластомера очень обширна. Относительное удлинение у него значительно выше, чем, например, у стали или гипса. Эластомер эластичен по своей природе, и, подобно резине, он восстанавливает свои исходные размеры сразу же после снятия напряжения. Кроме того, резина обладает крайне низкой прочностью при растяжении.
Образование шейки при испытании на растяжение
При упругой деформации наблюдается небольшое увеличение объема материала за счет того, что расстояние между атомами, из которых состоит твердое тело, удлиняется при растяжении. Однако при пластической деформации таких изменений объема не наблюдается. При такой деформации увеличение длины материала может привести к уменьшению площади его поперечного сечения. Это в свою очередь приведет к возникновению локализованной области материала, которая представлена на Рис. 1.7.6. Эта область уменьшения поперечного сечения образца называется шейкой. Часто такое явление наблюдается при растяжении материалов с повышенной вязкостью (пластичных материалов).

Рис. 1.7.6. Образование «шейки» при растяжении пластичного материала
Результаты испытаний на растяжение могут быть очень полезными при создании новых конструкций, поскольку для того, чтобы предсказать поведение конструкции, находящейся под нагрузкой, необходимо знание параметров упругой деформации материала.
Максимальное напряжение, которое может безопасно выдержать материал, определяется пределом текучести. Следовательно, от предела текучести зависит максимальная нагрузка, которой этот материал способен противостоять, хотя благоразумнее было бы включить в расчеты некоторый коэффициент запаса прочности.
Жесткость материала можно рассчитать по модулю упругости. Например, сочетание этих двух свойств (предела текучести и жесткости) позволит легко определить упругость или пружинистость металлической проволоки.
Если в технологический процесс изготовления продукции включены такие операции, как прокатка, протяжка проволоки или прессование, необходимо знать величину пластической деформации, которую материал сможет выдержать без разрушения. Если материал обладает высокой пластичностью, то ему можно придавать нужную форму, однако если пластичность материала невысока, то создание формы путем воздействия нагрузки будет невозможным.
Испытание на сжатие
Испытания на растяжение проводить сложно, особенно, если материал хрупкий — в таких случаях наблюдается большой разброс результатов. Альтернативным методом оценки прочности материала является испытание на сжатие, которое легче провести, если материал хрупкий, так как в этом случае разброс результатов будет меньшим. Другой причиной, по которой хрупкие образцы следует испытывать на сжатие, является тот факт, что эти материалы используются в условиях, где действуют сжимающие нагрузки.
На Рис. 1.7.7 схематически представлено проведение испытания на сжатие. Поскольку образец удерживается за счет трения в точках контакта с опорными пластинами испытательного прибора, здесь наблюдается увеличение площади поперечного сечения в середине образца, и одновременно с этим материал приобретает форму бочонка. Этот эффект «приобретения формы бочонка» приводит к возникновению очень сложной модели распределения напряжений в материале (также представленной на Рис. 1.7.7). Анализировать такую модель очень сложно. Это затрудняет интерпретацию результатов испытаний на сжатие.

Рис. 1.7.7. Распределение напряжений растяжения и сдвига в образце при определении прочности материала на сжатие
Компромиссным испытанием является измерение так называемой диаметральной прочности, в который изготовленный из испытываемого материала диск подвергают воздействию сжимающей нагрузки. В результате приложения этой нагрузки к диску, в направлении, перпендикулярном направлению приложения сжимающей нагрузки, возникают напряжения растяжения, что схематически представлено на Рис. 1.7.8.

Рис. 1.7.8. Схема испытания образца для определения прочности материала на диаметральный разрыв
Растягивающее напряжение, а, рассчитывают по формуле:
а = 2P/JT.DT,
где Р — нагрузка, D — диаметр диска, Т — толщина диска. Обычно этот метод используют для испытаний хрупких стоматологических материалов, поскольку он прост и позволяет получать более воспроизводимые результаты, чем в случае испытаний на растяжение.
Испытание твердости
Испытание твердости — это измерение сопротивления поверхности материала воздействию инструмента, внедряемого или вдавливаемого в поверхность (индентеров), или режущего инструмента. Испытание твердости проводят для определения сопротивления материала царапанью или стиранию. Кроме того, существует приближенная зависимость между твердостью материала и пределом прочности на растяжение.
Для испытаний используют индентер в форме шарика (при испытании твердости по Бринелю), пирамидки (при испытании твердости по Виккерсу или по Кнуппу) или конуса (при испытании твердости по Роквеллу). Разумеется, твердость самого индентера должна быть выше твердости испытываемого материала. Образец вдавливают в поверхность материала в течение определенного периода времени, и на поверхности материала остается отпечаток шарика, пирамидки или конуса (Рис. 1.7.9).

Рис. 1.7.9 Вид отпечатка индентера на поверхности образца для различных видов твердомеров
Размер полученного отпечатка будет зависеть от твердости испытуемого материала. Размеры отпечатка можно измерить и подсчитать из них эмпирическое значение числа твердости. Выбор метода испытания твердости до некоторой степени зависит от природы материала, который будет подвергнут испытанию.
Испытание на ударную прочность
Испытание на ударную прочность — это оценка сопротивления материала мгновенному приложению нагрузки. Стандартный образец в виде балки с насечками подвергают воздействию импульсной нагрузки, создаваемой маятниковым копром. Схематическое изображение испытания на ударную прочность представлено на Рис. 1.7.10.

Рис. 1.7.10. Расположение образца при определении прочности на удар по Шарли. Маятник с ударником, который падает с определенной высоты
Маятниковый копер отпускают с определенной высоты, он ударяет и разрушает образец, который установлен на параллельных опорах. Часть энергии маятника используется для разбивания образца. Если будут известны начальная высота, на которой находился маятник, и высота, на которую он поднялся после разрушения образца, то нетрудно будет рассчитать разницу энергий. Эта разница является мерой количества энергии, которая была поглощена образцом, что и вызвало его разрушение. Несмотря на то, что результаты этого испытания являются эмпирическими, его можно применять для оценки ударной прочности ряда материалов. Присутствие насечек на образце делает условия проведения испытания очень жесткими, а также является показателем чувствительности материала к присутствию надрезов на его поверхности.
Испытание на усталостную прочность
Во многих практических ситуациях материалы подвергаются воздействию переменных нагрузок чаще, чем статических, о которых говорилось выше. Постепенное накопление незначительных количеств пластической деформации, возникающих в результате воздействия цикла переменных напряжений, известно под названием усталости материала.
Усталость может стать причиной разрушения материала при напряжениях, величина которых значительно ниже предела текучести. Для проведения испытания на усталостную прочность образцы материала подвергают воздействию циклических нагрузок в некотором их диапазоне. В каждом случае подсчитывают число циклов, требуемых для разрушения образцов.
Величину напряжения выражают графически в виде логарифмической зависимости от соответствующего числа циклов напряжений, которое требуется для разрушения образца. Кривая зависимости напряжения от числа циклов (кривая Н — Ч) представлена на Рис. 1.7.11.

Рис. 1.7.11.
Существуют две формы поведения материалов. Для некоторых материалов по мере увеличения числа циклов нагрузки происходит снижение напряжений, которые способен выдержать материал. Однако для других материалов существует уровень напряжений, называемый пределом выносливости, ниже которого материал можно подвергать неопределенному числу циклов нагрузки, не вызывая его разрушения.
Усталостная прочность в значительной степени определяется характеристиками поверхности материала. Улучшение качества обработки поверхности или создание на поверхности напряжений сжатия механическими, термическими или химическими методами, приводит к повышению усталостной кривой Н — Ч.
Кроме того, на характер кривой Н — Ч выраженное влияние оказывает среда, в которой проходит эксперимент. Например, в коррозионных средах усталостная прочность материала снижается.
Клиническое значение
В некоторых случаях материал может быть достаточно прочным, чтобы выдерживать нагрузки в начале его использования в полости рта, но это не означает, что он сможет противостоять таким же нагрузкам в отдаленные сроки клинической службы.
Испытание на крип (ползучесть)
Если материал долгое время находится под нагрузкой, то под воздействием постоянного напряжения он может непрерывно деформироваться, даже несмотря на то, что величины действующих на него напряжений значительно ниже предела упругости. Эта деформация материала, зависящая от времени его нахождения под нагрузкой, называется крипом, который, в конечном итоге, ведет к разрушению материала. В частности, понимание этого явления важно, если материал используют при температурах, превышающих половину значения температуры плавления или температуры размягчения, что, например, характерно для некоторых амальгамных фаз или многих пластических материалов. При температурах на 40 — 50% меньше абсолютной точки плавления материала, крип ничтожно мал.
На Рис. 1.7.12 представлена типичная кривая крипа. На ней можно выделить 4 стадии деформации:
• начальное удлинение, возникшее в результате приложения нагрузки;
• переходный или первичный крип, который стремится к непрерывному увеличению;
• устойчивое состояние (вторичный крип);
• третичный крип.

Рис. 1.7.12. Кривая крипа, на которой можно выделить четыре стадии ползучести в условиях долговременных испытаний при высокой температуре
Клиническое значение
Механические свойства материалов можно определять в широких пределах. Это позволяет сравнивать между собой разные стоматологические материалы, хотя значение результатов таких испытаний для клиники остается предметом многочисленных дебатов.
Основы стоматологического материаловедения
Ричард ван Нурт
Опубликовал Константин Моканов
Источник
Отвечает эксперт ЗАО ЦНИИПСК им. Мельникова
Испытание на растяжение металла заключаются в растяжении образца с построением графика зависимости удлинения образца (Δl) от прилагаемой нагрузки (P), с последующим перестроением этой диаграммы в диаграмму условных напряжений (σ — ε)
Испытания на растяжение проводятся по ГОСТ 1497, по этому же ГОСТу определяются и образцы на которых проводятся испытания.
Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
- Участок ОА — участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
- Участок ОВ — участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении
Выше точки В диаграмма растяжения отходит от прямой — деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.
Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение — шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.
Прилагаемая нагрузка для растяжения образца зависит от геометрии этого образца. Чем больше площадь сечения, тем более высокая нагрузка необходима для растяжения образца. По этой причине, получаемая машинная диаграмма не дает качественной оценки механических свойств материала. Чтобы исключить влияние геометрии образца, машинную диаграмму перестраивают в координатах σ − ε путем деления ординат P на первоначальную площадь сечения образца A0 и абсцисс ∆l на lо. Перестроенная таким образом диаграмма называется диаграммой условных напряжений. Уже по этой, новой диаграмме, определяют механические характеристики материала.
Определяются следующие механические характеристики:
Предел пропорциональности σпц – наибольшее напряжение, после которого нарушается справедливость закона Гука σ = Еε , где Е – модуль продольной упругости, или модуль упругости первого рода. При этом Е =σ/ε = tgα , т. е. модуль E это тангенс угла наклона прямолинейной части диаграммы к оси абсцисс
Предел упругости σу — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σу
Предел текучести σт – напряжение, при котором происходит увеличение деформации без заметного увеличения растягивающей нагрузки
Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести
Предел прочности (временное сопротивление разрыву) σв – напряжение, соответствующее наибольшей нагрузке Pmax , предшествующей разрыву образца
Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности — относительное удлинение δ и относительное сужение ψ
где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца
Источник
