Жесткость на растяжение трубы

Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
ГлавнаяСтатьи и материалыКольцевая жёсткость труб
содержание
Кольцевая жёсткость труб
Основные понятия кольцевой жесткости
В процессе исследований было установлено, что трубы с гибкими поверхностями более восприимчивы к нагрузкам, которые передаются через почву, нежели трубы с жёсткими стенками. Грунт может иметь разную степень уплотнения, которая влияет на выбор кольцевой жёсткости.
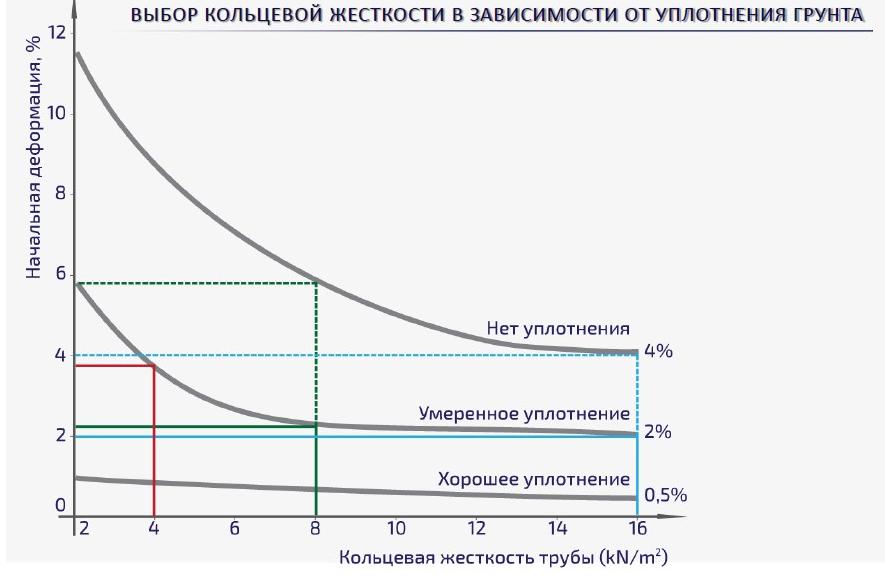
Чем больше кольцевая жёсткость, тем более высокие нагрузки может выдерживать труба. Данный показатель измеряется в кН/м2. От него зависит область использования труб и условия их монтажа.
Классы жёсткости SN
Все полимерные трубы имеют свой класс жёсткости, который указывает какую именно нагрузку способно выдержать то или иное изделие. Значение данного параметра принято исчислять с шагом в степенях числа два. То есть класс жёсткости (SN) у полимерных труб может равняться 2, 4, 8 и т.д.
- SN 2 – трубы с таким классом жёсткости могут располагаться на глубине от 1 м и более, но они не предназначены для эксплуатации в условиях нагрузок от транспортных средств;
- SN 4 – такие изделия могут закладываться на глубину от 1 м и больше. Рассчитаны на использование в местах, где планируется движение легкового автотранспорта;
- SN 8 – также могут укладываться на расстоянии от 1 м и больше от поверхности земли, но по сравнению с трубами предыдущего класса, способны ещё выдерживать нагрузки от грузовых машин.
При определении глубины заложения учитывается степень уплотнения почвы.
Как тип грунта связан с классом жёсткости
При выборе труб по классу жёсткости также учитывается тип почвы. Чем менее цепкая почва и большая нагрузка на грунт, тем выше требования жёсткости.
| Условия прокладки | Материал засыпки трубы | Рекомендуемая минимальная жесткость труб (kN/м) | |||||
|---|---|---|---|---|---|---|---|
| Глубина укладки труб | 3 — 6 м | ||||||
| Плотный грунт с хор. сцеп-ем | Насосы и плотн. глина | Разрых. глина | Плотный грунт с хор. сцеп-ем | Насосы и плотн. глина | Разрых. глина | ||
| Естественный грунт (нет нагрузки от наземного транспорта) | Местный грунт | 2 | — | — | 4 | — | — |
| 2 | 4 | 8 | 4 | 8 | 16 | ||
| Песок, гравия | 2 | 4 | 8 | 4 | 4 | 8 | |
| Галька, щебень 4 — 22 мм | 2 | — | — | 4 | — | — | |
| Второстепенны! улицы с незначительной интенсивности движения транспорта | Местный грунт | 4 | 4 | 8 | 4 | 8 | 16 |
| Песок, гравия | 4 | 4 | 4 | 4 | 4 | 8 | |
| Галька, щебень 4 — 22 мм | 4 | — | — | 4 | — | — | |
| Главные улицы с интенсивным движением транспорта | Местный грунт | 8 | — | — | 8 | — | |
| Песок, гравия | 8 | 8 | 8 | 8 | 8 | 8 | |
| Галька, щебень 4 — 22 мм | 8 | — | — | 8 | — | — | |
Как увеличить кольцевую жёсткость
Для увеличения данного показателя следует:
- Использовать материалы с более высоким модулем упругости. Если нужно выбрать, какой материал использовать, например, ПВХ либо полиэтилен, то стоит отдать предпочтение поливинилхлориду;
- Повысить модуль инерции стенки трубопроводного изделия. Этого можно добиться разными способами. Толщина стенок может быть увеличена не только традиционным путём, но и за счёт применения профилированных (ребристых) конструкций.
Жёсткость труб из разных материалов
Трубы ПВХ
| Номинальный диаметр труб | SN 2 | SN 4 | SN 8 | |||
|---|---|---|---|---|---|---|
| Толщина стенки мм. | Вес 1п/м (кг) | Толщина стенки мм. | Вес 1п/м (кг) | Толщина стенки мм. | Вес 1п/м (кг) | |
| 110 | 2.7 | 1.46 | 3.4 | 1.81 | 3.2 | 1.74 |
| 160 | 3.2 | 2.56 | 4.0 | 3.14 | 4.9 | 3.69 |
| 200 | 3.9 | 3.87 | 4.9 | 4.84 | 5.9 | 5.77 |
| 225 | — | — | 5.5 | 6.02 | 6.9 | 7.44 |
| 250 | 4.9 | 6.08 | 6.2 | 7.69 | 7.3 | 8.98 |
| 315 | 6.2 | 9.75 | 7.7 | 12.0 | 9.7 | 14.3 |
| 400 | 7.8 | 15.8 | 9.8 | 19.5 | 11.7 | 23.2 |
| 500 | 9.8 | 24.7 | 12.3 | 30.9 | 14.6 | 36.2 |
| 630 | — | — | 15.4 | 48.7 | 18.4 | 58.2 |
Трубы ПП двухслойные, гофрированные
| Трубы ПП для наружной канализации | Размер L, мм | de, мм внешний | DN, мм внутренний | Вес 1 кг/м SN4, SN 8 |
|---|---|---|---|---|
| 110×6000 | 110 | 93 | 0.6 | |
| 160×6000 | 137 | 160 | 1.3 | |
| 200×6000 | 227 | 200 | 2.3; 2,7 | |
| 250х6000 | 282 | 250 | 3,5 | |
| 300х6000 | 340 | 300 | 4,4; 5,1 | |
| 400х6000 | 453 | 400 | 7,2; 9,0 | |
| 500х5900 | 567 | 500 | 10,95; 14,5 | |
| 600х5900 | 680 | 600 | 15,8; 20,5 | |
| 800х5850 | 906 | 800 | 26,04; 32,5 | |
| 1000х5850 | 1135 | 1000 | 40,6 |
Трубы ПНД
| Тип технической трубы | Значение, кН/м2 |
|---|---|
| Тип «Л» (SDR33) | |
| Тип «СЛ» (SDR26) | 3 |
| Тип «ОС» (SDR21) | 5 |
| Тип «С» (SDR17,6) | 8 |
| Тип «с+» (SDR17) | 8 |
| Тип «СТ» (SDR13,6) | 18 |
| Тип «Т» (SDR11) | 32 |
Трубы корсис (двухслойные, профилированные)
| Наружный диаметр мм | Внутренний диаметр мм | Толщина стенки вн. слоя мм | Высота гофра мм | Толщина стенки гофра по жесткости | Шаг гофра мм | Ширина выступа гофра мм | Расчетная масса 1м трубы (кг) | ||
|---|---|---|---|---|---|---|---|---|---|
| SN-6 | SN8 | SN-6 | SN8 | ||||||
| 110 | 93 | 1.1 | 8.75 | — | 0.5 | 12.6 | 8.6 | 0.9 | 1.0 |
| 139 | 1.2 | 11 | — | 0.5 | 12.6 | 8.6 | 0.9 | 1.0 | |
| 200 | 176 | 1.4 | 13 | 0.7 | 0.8 | 16.5 | 12 | 1.8 | 2.5 |
| 250 | 216 | 1.7 | 15 | 0.8 | 1 | 37 | 23 | 2.9 | 3.7 |
| 315 | 271 | 1.9 | 21 | 1 | 1.5 | 42 | 27 | 4.6 | 5.7 |
| 400 | 343 | 2.3 | 26 | 1 | 1.8 | 49 | 30 | 7.0 | 8.7 |
| 500 | 427 | 2.8 | 33 | 1.1 | 1.9 | 58 | 38 | 12.0 | 13.2 |
| 630 | 535 | 3.3 | 45 | 1.1 | 1.9 | 75 | 47 | 17.7 | 20.3 |
| 800 | 678 | 4.1 | 61 | 1.7 | 2.7 | 89 | 56 | 24.5 | 33.1 |
| 1000 | 851 | 5 | 75 | 1.8 | 2.8 | 98 | 60 | 40.5 | 51.7 |
| 1200 | 1030 | 5 | 85 | 2 | 3 | 110 | 80 | 56.0 | 66.9 |
Трубы ПЭ
| Внутренний диаметр, мм | Максимальный внешний диаметр, (мм) для труб с кольцевой жесткостью | Внутренний диаметр, мм | Максимальный внешний диаметр, (мм) для труб с кольцевой жесткостью | ||||
|---|---|---|---|---|---|---|---|
| Номинальное значение | Предельное отклонение | SN2 | SN4 | SN6 | Номинальное значение | Предельное отклонение | SN2 |
| 600 | -18 | 648 | 656 | 672 | 3600 | -80 | 3864 |
| 800 | 858 | 874 | 896 | 3800 | 4080 | ||
| 1000 | -60 | 1072 | 1094 | 1120 | 4000 | 4296 | |
| 1200 | 1288 | 1314 | 1344 | 4200 | -100 | 4512 | |
| 1400 | 1504 | 1532 | 1568 | 4400 | 4728 | ||
| 1600 | 1718 | 1752 | 1792 | 4600 | 4944 | ||
| 1800 | 1934 | 1970 | 2016 | 4800 | 5160 | ||
| 2000 | 2150 | 2190 | 2240 | 5000 | 5376 | ||
| 2400 | 2576 | 2628 | 2688 | 5200 | -120 | 5592 | |
| 2550 | 2742 | 2794 | 2862 | 5400 | 5806 | ||
| 3000 | 3222 | 3286 | 3364 | 5600 | 6022 | ||
| 3200 | -80 | 3436 | 5800 | 6234 | |||
| 3400 | 3650 | 6000 | 6450 | ||||
Как правильно выбрать материал трубы с учётом кольцевой жесткости
Выбор труб по кольцевой жёсткости в первую очередь зависит от условий эксплуатации канализационной коммуникации и возможных нагрузок. Так, например, безнапорные поливинилхлоридные трубы D = 110-200 мм с SN 2 получили широкое распространение для создания канализационных систем в частном секторе, но они не подходят для использования в промышленных и коммунальных целях. В этом случае оптимальным вариантом станут полипропиленовые 2-слойные гофрированные трубы D = 300 мм и больше с SN 8 или SN 16.
По показателям кольцевой жёсткости трубы из полиэтилена проигрывают аналогичным изделиям из полипропилена. Ввиду невысокой кольцевой жёсткости ПЭ трубопроводы нельзя сильно заглублять, поскольку под воздействием давления со стороны грунта произойдёт деформация труб.
Расчёт кольцевой жёсткости трубы
Расчётные данные кольцевой жёсткости труб получают экспериментально при испытаниях изделий на специальных стендах. При этом выбирается отрезок трубы и определяется нагрузка и деформация, которая соответствует деформации примерно 4% тестируемого изделия. Испытаниям подвергаются три экземпляра из партии, определяется среднеарифметическое число, которое округляется до наиболее близкого минимального стандартного показателя. То есть от класса жёсткости зависит, какая номинальная нагрузка может приходится на единицу площади изделия в случае 4-процентной деформации сечения по вертикали, не учитывая отпора сбоку.
Для определения SN применяется формула:
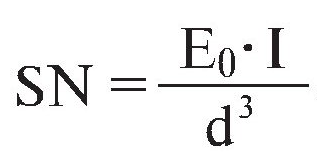
Где:
E0 – модуль упругости материала, из которого изготовлено изделие;
I – момент инерции стенки изделия;
d – диаметр, который измеряется в месте центра тяжести стенки изделия, и равен:
Где:
di – внутренний диаметр изделия;
y – расстояние до центра тяжести стенки изделия.
Выбор труб для внешней канализации с учётом кольцевой жесткости
При выборе труб для создания внешней канализационной сети, важно учитывать показатели кольцевой жёсткости. Это позволит в будущем избежать неприятных ситуаций и обеспечит бесперебойную длительную эксплуатацию трубопровода. Несоблюдение требований по классу жёсткости грозит деформацией трубопровода. А это способно привести к снижению эффективности работы системы и преждевременному выходу её из строя, а, следовательно, дополнительным расходам на её восстановление.
Трубы с высокой кольцевой жесткостью
трубы для водоснабжения из сырья Fusiolen произведенные в Германии.
- Коэффициент линейного расширения составляет 0,035 мм/м
- Низкий коэффициент теплопроводности — всего 0.15 Вт/м*K
- Рабочая температура 95 градусов, давление 10 бар
- Гарантия 10 лет и 20 миллионов Евро
- Срок службы до 100 лет (Сертификат DVS)
трубы для водоснабжения из сырья Fusiolen произведенные в Германии.
- Коэффициент линейного расширения составляет 0,035 мм/м
- Низкий коэффициент теплопроводности — всего 0.15 Вт/м*K
- Рабочая температура 95 градусов, давление 10 бар
- Гарантия 10 лет и 20 миллионов Евро
- Срок службы до 100 лет (Сертификат DVS)
- Регламентом для использования НПВХ труб в канализационных системах является ГОСТ 32413-2013.
- Шумопоглощение 12 Db
- Напорная (10 бар) и безнапорная система (3 бара)
- Группа горючести Г1
Вопросы, комментарии, отзывы
Чтобы задать любой интересующий Вас вопрос, отправить запрос на расчет продукции или запросить необходимую документацию Вы можете воспользоваться специальной формой на сайте, отправить письмо по электронной почте или позвонить по телефону
Источник
