Закон гука при растяжении и сжатии пружины
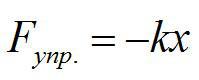
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Механика
Силы в природе
1.12. Сила упругости. Закон Гука
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).
| Рисунок 1.12.1. Деформация растяжения ( x > 0 ) и сжатия ( x < 0 ). Внешняя сила |
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
| Рисунок 1.12.2. Деформация изгиба. |
Упругую силу действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: Сила с которой тело действует на стол, называется весом тела.
В технике часто применяются спиралеобразные пружины (рис. 1.12.3). При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
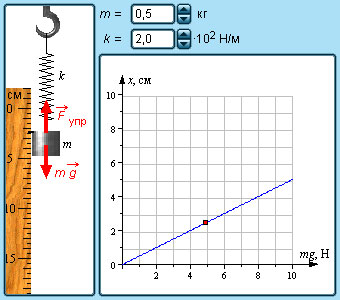 |
Модель. |
Источник
Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация — изменение положения частиц тела друг относительно друга. Результат деформации — изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости — сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации — растяжение и сжатие
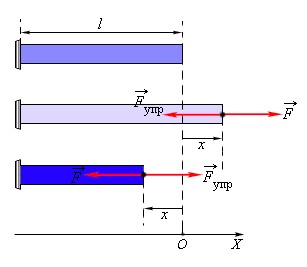
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Закон Гука
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k — коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S — площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E — так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
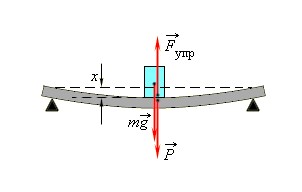
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела — это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого — динамаметр.
Динамометр — пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения — текучесть и разрушения.
Источник
Физика, 10 класс
Урок 9. Закон Гука
Перечень вопросов, рассматриваемых на этом уроке
1.Закона Гука.
2.Модели видов деформаций.
3. Вычисление и измерение силы упругости, жёсткости и удлинение пружины.
Глоссарий по теме
Сила упругости – это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.
Деформация – изменение формы или размеров тела, происходящее из-за неодинакового смещения различных частей одного и того же тела в результате воздействия другого тела. Виды деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
Закон Гука – сила упругости, возникающая при деформации тела (растяжение или сжатие пружины), пропорциональна удлинению тела (пружины), и направлена в сторону противоположную направлению перемещений частиц тела
Основная и дополнительная литература по теме:
Г.Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр. 107-112
Рымкевич А.П. Сборник задач по физике. 10-11класс.- М.:Дрофа,2009. Стр 28-29
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Основное содержание урока
В окружающем нас мире мы наблюдаем, как различные силы заставляют тела двигаться, делать прыжки, перемещаться, взаимодействовать.
Однако можно также наблюдать как происходят разрушения, так называемые деформации, различных сооружений: мостов, домов, разнообразных машин.
Что необходимо знать инженеру конструктору, строителю, чтобы строить надёжные сооружения: дома, мосты, машины?
Почему деформации различны, какие виды деформации могут быть у конкретных тел? Почему одни тела после деформации могут восстановиться, а другие нет? От чего зависит и можно ли рассчитать величину этих деформаций?
Деформация — это изменение формы или размеров тела, в результате воздействия на него другого тела.
Почему деформации не одинаковы у различных тел, если мы их, к примеру, сжимаем? Давайте вспомним что мы знаем о строении вещества.
Все вещества состоят из частиц. Между этими частицами существуют силы взаимодействия- эти силы электромагнитной природы. Эти силы в зависимости от расстояний между частицами проявляются, то как силы притяжения, то как силы отталкивания.
Сила упругости – сила, возникающая при деформации любых тел, а также при сжатии жидкостей и газов. Она противодействует изменению формы тел.
Мы можем наблюдать несколько видов деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
При деформации растяжения межмолекулярные расстояния увеличиваются. Такую деформацию испытывают струны в музыкальных инструментах, различные нити, тросы, буксирные тросы.
При деформации сжатия межмолекулярные расстояния уменьшаются. Под такой деформацией находятся стены, фундаменты сооружений и зданий.
При деформации изгиба происходят неординарные изменения, одни межмолекулярные слои увеличиваются, а другие уменьшаются. Такие деформации испытывают перекрытия в зданиях и мостах.
При кручении – происходят повороты одних молекулярных слоёв относительно других. Эту деформацию испытывают: валы, витки цилиндрических пружин, столярный бур, свёрла по металлу, валы при бурении нефтяных скважин. Деформация среза тоже является разновидностью деформации сдвига.
Первое научное исследование упругого растяжения и сжатия вещества провёл английский учёный Роберт Гук.
Роберт Гук установил, что при малых деформациях растяжения или сжатия тела абсолютное удлинение тела прямо пропорционально деформирующей силе.

F упр = k ·Δℓ = k · Iℓ−ℓ0I закон Гука.
k− коэффициент пропорциональности, жёсткость тела.
ℓ0 — начальная длина.
ℓ — конечная длина после деформации.
Δℓ = I ℓ−ℓ₀ I- абсолютное удлинение пружины.
 — единица измерения жёсткости в системе СИ.
— единица измерения жёсткости в системе СИ.
При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе, а слишком большие деформации разрушают тело.
Для расчёта движения тел под действием силы упругости, нужно учитывать направление этой силы. Если принять за начало отсчёта крайнюю точку недеформированного тела, то абсолютное удлинение тела можно характеризовать конечной координатой деформированного тела. При растяжении и сжатии сила упругости направлена противоположно смещению его конца.
Закон Гука можно записать для проекции силы упругости на выбранную координатную ось в виде:
F упр x = − kx — закона Гука.
k – коэффициент пропорциональности, жёсткость тела.
x = Δℓ = ℓ−ℓ0 удлинение тела (пружины, резины, шнура, нити….)
Fупр x = − kx
Закон Гука:
Fупр = k·Δℓ = k · Iℓ−ℓ0I
Графиком зависимости модуля силы упругости от абсолютного удлинения тела является прямая, угол наклона которой к оси абсцисс зависит от коэффициента жёсткости k. Если прямая идёт круче к оси силы упругости, то коэффициент жёсткости этого тела больше, если же уклон прямой идёт ближе к оси абсолютного удлинения, следует понимать, что жёсткость тела меньше.

График, зависимости проекции силы упругости на ось ОХ, того же тела от значения х.

Необходимо помнить, что закон Гука хорошо выполняется при только при малых деформациях. При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе.
Разбор тренировочных заданий
1. По результатам исследования построен график зависимости модуля силы упругости пружины от её деформации. Чему равна жёсткость пружины? Каким будет удлинение этой пружины при подвешивании груза массой 2кг?

Решение: По графику идёт линейная зависимость модуля силы упругости и удлинение пружины. Зависимость физических величин по Закону Гука:
F упр x = − kx (1)
Fупр =k·Δℓ = k · Iℓ−ℓ0I (2)
Из формулы (1) выражаем:

Зная что Fт = mg = 20 Н, Fт = Fупр= k·Δℓ следовательно

Ответ: жёсткость пружины равна 200 Н/м, удлинение пружины равно 0,1м.
2. К системе из кубика массой 1 кг и двух пружин приложена постоянная горизонтальная сила. Система покоится. Между кубиком и опорой трения нет. Левый край первой пружины прикреплён к стенке. Удлинение первой пружины 0,05 м. Жёсткость первой пружины равна 200 Н/м. Удлинение второй пружины 0,25 м.

- Чему равна приложенная к системе сила?
- Чему равна жёсткость второй пружины?
- Во сколько раз жёсткость второй пружины меньше чем первой?
Решение:
1. По условию задачи система находится в покое. Зная жёсткость и удлинение пружины найдём силу, которая уравновешивает приложенную постоянную горизонтальную силу.
F = F упр =k1·Δℓ1= 200 Н/м·0,05 м = 10 Н
2. Жёсткость второй пружины:

3. k1/ k2 = 200/40 = 5
Ответ: F=10 Н; k2 = 40 Н/м; k1/k2 = 5.
Источник
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
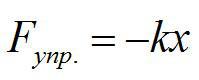
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
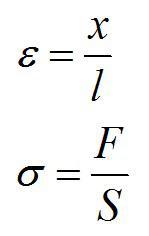
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
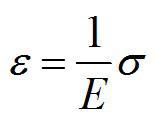
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
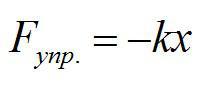
По третьему закону Ньютона:
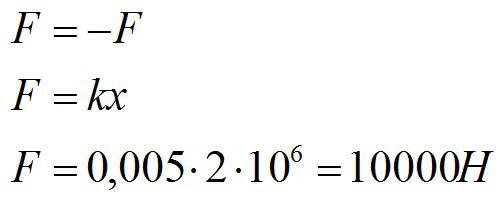
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
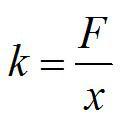
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
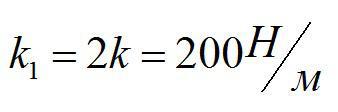
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
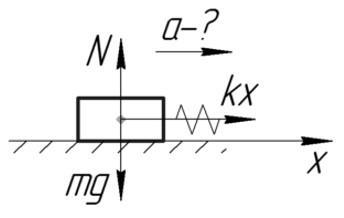
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
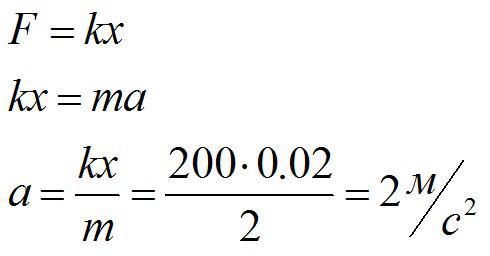
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
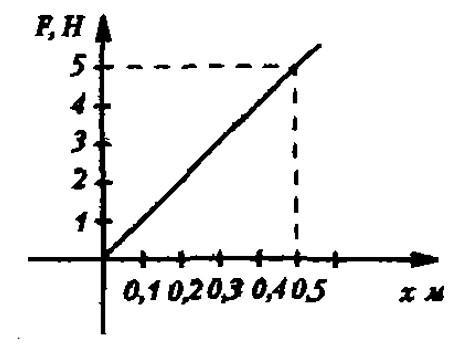
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
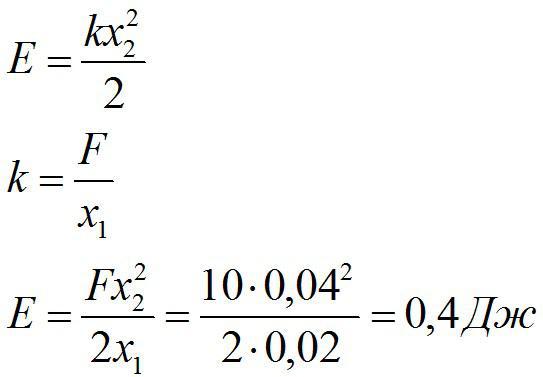
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Автор
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
Сопротивление материалов
Деформации при растяжении и сжатии
Продольные деформации при растяжении и сжатии
Характер деформаций, которым подвергается прямой брус при растяжении или сжатии мы определили, проведя опыт с резиновым брусом, на котором была нанесена сетка линий.
Теперь представим себе брус постоянного сечения имеющий длину l, один из концов которого защемлен, а к свободному концу приложена растягивающая сила F. Под действием этой силы брус удлинится на некоторую величину Δl, которую назовем абсолютным удлинением бруса.
Отношение абсолютного удлинения Δl к первоначальной длине бруса l назовем относительным удлинением и обозначим ε:
ε = Δl / l
Относительное удлинение – величина безразмерная, иногда его выражают в процентах.
Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.
***
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой линейной зависимостью, которая называется законом Гука, по имени английского физика Р. Гука (1653-1703 г.г.), установившего этот закон.
Сформулировать закон Гука можно так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.
Математически эта зависимость записывается так:
σ = E ε.
Здесь Е – коэффициент пропорциональности, который характеризует жесткость материала бруса, т. е. его способность сопротивляться деформации; его называют модулем продольной упругости, или модулем упругости первого рода.
Модуль упругости, как и напряжение, выражаются в паскалях (Па).
Значения Е для различных материалов устанавливаются экспериментально-опытным путем, и их величину можно найти в соответствующих справочниках.
Так, для стали Е = (1,96.…2,16) х 105 МПа, для меди Е = (1,00…1,30) х 105 МПа и т. д.
Следует оговориться, что закон Гука справедлив лишь в определенных пределах нагружения.
Если в формулу закона Гука подставить полученные ранее значения относительного удлинения и напряжения: ε = Δl / l , σ = N / А, то можно получить следующую зависимость:
Δl = Nl / (EА).
Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.
Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение ЕА / l называют жесткостью бруса при растяжении и сжатии.
Приведенные выше формулы закона Гука справедливы лишь для брусьев и их участков, имеющих постоянное поперечное сечение, изготовленных из одного материала и при постоянной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами сечения, продольной силой, изменение длины всего бруса определяется, как алгебраическая сумма удлинений или укорочений отдельных участков:
Δl = Σ (Δli)
***
Поперечные деформации при растяжении и сжатии
Описанный ранее опыт с резиновым брусом, на котором нанесена сетка линий, показал, что при растяжении поперечные размеры бруса уменьшаются, а при сжатии – увеличиваются, т. е. брус становится либо тоньше, либо толще. Это явление характерно для брусьев, изготовленных из всех материалов.
Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций для данного материала – величина постоянная.
Впервые на эту зависимость указал французский ученый С. Пуассон (1781-1840 г.г.) и математически она записывается так:
|ε1| = ν |ε|,
где ν – коэффициент поперечной деформации, называемый коэффициентом Пуассона.
Коэффициент Пуассона является безразмерной величиной, и характеризует упругие свойства материала. При растяжении и сжатии этот коэффициент принимается одинаковым.
Значения коэффициента Пуассона для разных материалов установлены опытным путем и их величины можно найти в соответствующих справочниках.

***
Потенциальная энергия деформации при растяжении
При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W.
Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что W = U.
Путем изучения диаграмм растяжения образцов, установлено, что потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна:
U = W = F Δl / 2 = N2 l / (2E А)
Сопротивление материалов оперирует, также, таким понятием, как удельная потенциальная энергия деформации, которая подсчитывается, как потенциальная энергия, приходящаяся на единицу объема бруса.
При одновременном действии растягивающих и сжимающих нагрузок или ступенчатом изменении размеров поперечного сечения бруса, его разбивают на однородные участки и для каждого подсчитывают потенциальную энергию деформации. Потенциальную энергию деформации всего бруса определяют, как сумму потенциальных энергий отдельных участков.
Анализируя формулу потенциальной энергии деформации можно сделать вывод, что эта величина всегда положительная, поскольку в ее выражения входят квадраты линейных и силовых величин. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (поскольку квадрат суммы не равен сумме квадратов слагаемых).
Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж).
***
Материалы раздела «Растяжение и сжатие»:
- Основные понятия о деформации растяжения и сжатия.
- Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.
Смятие
Правильные ответы на вопросы Теста № 5
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 3 | 3 | 1 | 2 | 1 | 3 | 2 | 2 | 1 | 1 |
Источник
