Внецентренное растяжение бруса это
Внецентренным растяжением или сжатием называется такой вид деформации, когда в поперечном сечении бруса одновременно действуют продольная (растягивающая или сжимающая) сила и. изгибающий момент; в этом сечении может действовать и поперечная сила.
Внецентренно растянутый или сжатый брус, при расчете которого можно не учитывать дополнительные изгибающие моменты, равные произведениям продольных внешних сил Р на прогибы , называется жестким, а брус, при расчете которого их следует учитывать, — гибким.
Жесткими являются внецентренно сжатые и растянутые брусья, изображенные на рис. 10.9, а, г, д, если наибольшие их прогибы малы по сравнению с расстояниями сил Р от осей брусьев, и брусья, изображенные на рис. 10.9, б, в, в тех случаях, когда произведения малы по сравнению с внешними моментами
Рассмотрим расчет жестких брусьев; метод расчета гибких брусьев изложен ниже в § 5.13.
На рис. 11.9, а изображен жесткий брус; в его верхнем поперечном сечении одновременно действуют продольная сила N и изгибающий момент М, составляющие которого относительно главных осей и у инерции сечения равны Нормальное напряжение в произвольной точке С сечения с координатами у и равно сумме напряжений от продольной силы N и изгибающих моментов , т. е.
Продольная сила N и моменты могут рассматриваться как результат воздействия на брус внецентренно приложенной силы
Именно поэтому случай одновременного действия в поперечном сечении продольной силы и изгибающего момента называют внецентренным растяжением (при растягивающей продольной силе) или сжатием (при сжимающей).
Рис. 10.9
Координаты точки А приложения силы Р называются эксцентриситетами этой силы относительно главных осей инерции и у, соответственно:
Точку А приложения силы Р называют центром давления или полюсом.
Подставим в формулу (10.9) выражения [на основании формул (11.9) и рис. 1.9, б]:
Знаки плюс перед всеми членами этой формулы поставлены потому, что положительная продольная сила а также изгибающие моменты (при положительных эксцентриситетах ) вызывают в точках поперечного сечения с положительными координатами у и z растягивающие (положительные) напряжения.
В формулу (12.9) величина растягивающей силы Р подставляется со знаком плюс, а сжимающей — со знаком минус; координаты у и z в эту формулу подставляются со своими знаками. Знак нормальных напряжений, возникающих в какой-либо точке сечения от изгибающего момента вызванного эксцентрично (внецентренно) приложенной силой Р, можно установить также, представив поперечное сечение в виде пластинки, закрепленной на валу, ось которого совпадает с осью ; пластинка опирается на жесткое основание через систему пружин (рис. 12.9).
Момент от силы Р, показанной, например, на рис. 12.9, вызывает поворот пластинки вокруг оси z, в результате чего пружины, расположенные под заштрихованной частью пластинки, оказываются сжатыми; следовательно, в этой части сечения бруса от момента возникают сжимающие напряжения. Аналогично, для того чтобы установить знак напряжений от момента надо пластинку представить закрепленной на валу, ось которого совпадает с осью у.
Формула (12.9) служит для определения нормальных напряжений в любой точке поперечного сечения при внецентренном растяжении и сжатии.
Рис. 11.9
Формулу (12.9) можно представить в следующем виде:
ИЛИ
где — радиусы инерции поперечного сечения бруса относительно главных центральных осей инерции гну соответственно.
Следует иметь в виду, что в формулах (10.9)-(14.9) оси у и z являются главными центральными осями инерции поперечного сечения бруса.
Формулы (12.9)-(14.9) удобно использовать, когда известны равнодействующая внутренних усилий в поперечном сечении бруса (т. е. сила Р) и координаты точки ее приложения (полюса). Формулу же (10.9) удобно применять, когда известны внутренние усилия действующие в поперечном сечении.
Варианты эпюр нормальных напряжений, возникающих в поперечном сечении бруса при внецентренном сжатии (т. е. при отрицательной силе Р), изображены в аксонометрии на рис. 13.9.
Они ограничены с одной стороны плоскостью поперечного сечения 1-2-3-4, а с другой — плоскостью 1-2-3-4. Ординаты эпюр в центре тяжести сечения (при y = z = 0) равны
Рис. 12.9
Все ординаты эпюры, показанной на рис. 13.9, а, отрицательны, так как плоскость ограничивающая их, не пересекает плоскость 1-2-3-4 в пределах поперечного сечения бруса. Ординаты же эпюры, изображенной на рис. 13.9, б, по одну сторону от прямой отрицательны, а по другую — положительны.
Рис. 13.9
Прямая пп представляет собой линию пересечения плоскости 1-2-3-4 с плоскостью поперечного сечения бруса. Во всех точках, расположенных на прямой пп, напряжения а равны нулю, и, следовательно, эта прямая является нейтральной осью (нулевой линией).
Определим положение нейтральной оси (рис. 14.9). Для этого приравняем нулю правую часть выражения (14.9):
Так как , то
Выражение (15.9) является уравнением прямой (так как координаты у и входят в него в первой степени) и представляет собой уравнение нейтральной оси. Для определения положения нейтральной оси найдем ординату точки В ее пересечения с осью у (рис. 14.9); абсцисса этой точки а потому на основании выражения (15.9)
откуда
Рис. 14.9
Абсцисса точки С пересечения нейтральной оси с осью равна (рис. 14.9), а ордината этой точки Подставляя значения в выражение (15.9), находим
откуда
Итак, величины отрезков, отсекаемых нейтральной осью (нулевой линией) на осях координат, определяются выражениями:
Из этих выражений следует:
1) положение нулевой линии не зависит от величины и знака силы Р;
2) нулевая линия и полюс лежат по разные стороны от начала координат;
3) чем дальше от начала координат расположен полюс (т. е. чем больше по абсолютной величине координаты ), тем ближе к центру сечения проходит нейтральная ось (т. е. тем меньше отрезки ), и наоборот;
4) если полюс расположен на одной из главных центральных осей инерции, то нулевая линия перпендикулярна этой оси; например, когда полюс расположен на оси , то т. е. нейтральная ось параллельна оси у.
При внецентренном растяжении и сжатии нормальные напряжения в каждой точке поперечного сечения бруса, как и при изгибе, прямо пропорциональны расстоянию от этой точки до нейтральной оси. Наибольшие напряжения возникают в точках поперечного сечения, наиболее удаленных от нейтральной оси.
Эпюра нормальных напряжений, значения которых отложены от линии, перпендикулярной нейтральной оси, показана на рис. 14.9.
Каждая ордината этой эпюры определяет величину нормальных напряжений, возникающих в точках поперечного сечения, расположенных на прямой DD, проходящей через эту ординату параллельно нейтральной оси. Для построения этой эпюры достаточно определить положение нейтральной оси и вычислить нормальные напряжения в одной из точек поперечного сечения (не расположенной на этой оси), например в центре тяжести сечения. С помощью такой эпюры наиболее просто определяются значения нормальных напряжений в любых точках поперечного сечения.
Расчет на прочность стержня, сжатого или растянутого внецентренно приложенными продольными внешними силами (т. е. при отсутствии поперечных сил), производится наиболее просто, так как в таком случае внутренние усилия одинаковы во всех поперечных сечениях каждого участка стержня. Это исключает необходимость определения опасного поперечного сечения, так как при стержне с постоянными поперечными размерами в пределах каждого участка все сечения одного участка являются равноопасными. При стержне же с переменными поперечными размерами опасным в пределах каждого участка является сечение наименьшего размера.
При наличии в поперечных сечениях стержня поперечных сил изгибающие моменты непрерывно изменяются по длине стержня, а потому определение опасного сечения становится более сложным. Обычно в таких случаях проводят проверку прочности, определяя нормальные напряжения в ряде сечений (которые предположительно могут оказаться опасными) и сопоставляя их с допускаемыми напряжениями.
Для определения положения опасных точек в сечении следует параллельно нейтральной оси провести линии, касающиеся контура сечения. Таким путем находят точки сечения, расположенные по обе стороны от нейтральной оси и наиболее удаленные от нее, которые и могут быть опасными.
При пластичном материале для проверки прочности достаточно определить напряжения в одной точке сечения в точке с наибольшим по абсолютной величине нормальным напряжением. При хрупком материале необходимо определить наибольшее растягивающее и наибольшее сжимающее напряжения, т. е. найти напряжения в двух точках (за исключением тех случаев, когда в сечении действуют напряжения одного знака).
Поперечная сила вызывает в поперечном сечении бруса касательные напряжения, которые определяются по формуле Журавского (см. § 8.7).
Рассмотрим частный случай внецентренного сжатия или растяжения, когда полюс А расположен на одной из главных осей инерции, например на оси у, т. е. случай, когда Для этого случая формула (10.9) принимает вид
и, следовательно,
При прямоугольном поперечном сечении, основание которого b параллельно оси , а высота h параллельна оси у (рис. 15.9), получаем
или
Нейтральная ось при этом перпендикулярна оси у.
Рис. 15.9
Рис. 16.9
Формула (19.9) позволяет легко установить зависимость между видом эпюры нормальных напряжений и величиной эксцентриситета продольной силы (рис. 15.9). При
и, следовательно, эпюра напряжений а имеет вид прямоугольника (рис. 16.9, а).
При напряжения имеют одинаковые знаки и, следовательно, эпюра а имеет вид трапеции (рис. 16.9, б).
Источник

11. 2. Внецентренное растяжение или сжатие брусьев большой жесткости
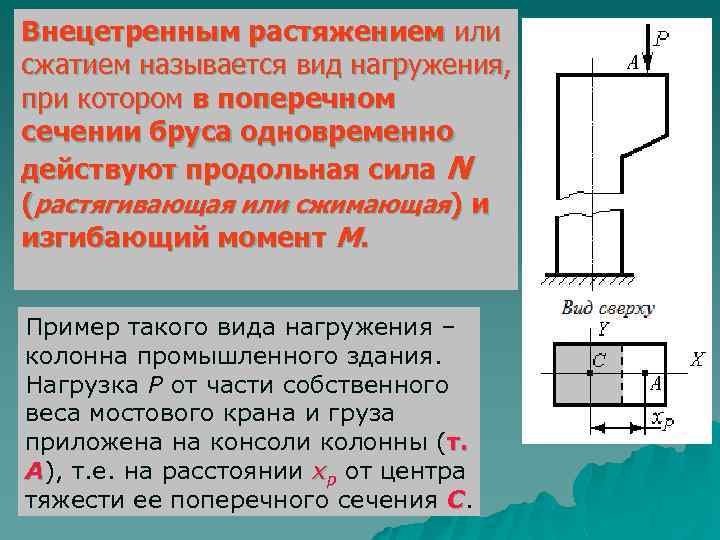
Внецетренным растяжением или сжатием называется вид нагружения, при котором в поперечном сечении бруса одновременно действуют продольная сила N (растягивающая или сжимающая) и изгибающий момент M. Пример такого вида нагружения – колонна промышленного здания. Нагрузка Р от части собственного веса мостового крана и груза приложена на консоли колонны (т. А), т. е. на расстоянии xp от центра тяжести ее поперечного сечения С.
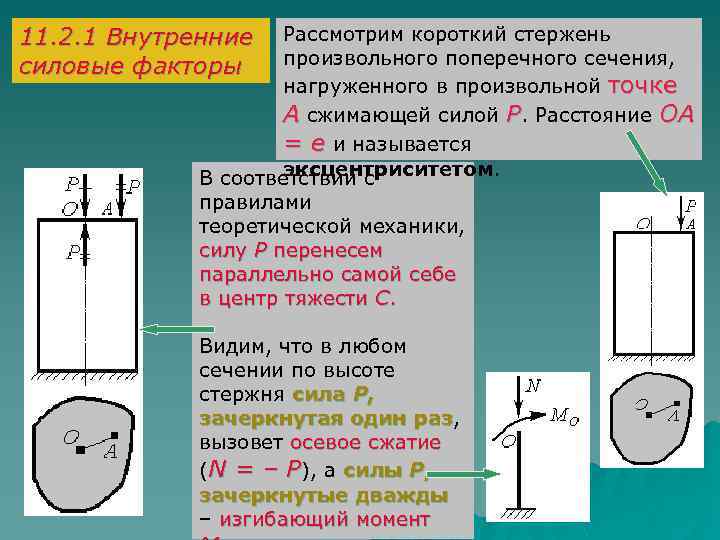
11. 2. 1 Внутренние силовые факторы Рассмотрим короткий стержень произвольного поперечного сечения, нагруженного в произвольной точке А сжимающей силой Р. Расстояние ОА = е и называется эксцентриситетом. В соответствии с правилами теоретической механики, силу Р перенесем параллельно самой себе в центр тяжести С. Видим, что в любом сечении по высоте стержня сила Р, зачеркнутая один раз, раз вызовет осевое сжатие (N = – P), а силы Р, зачеркнутые дважды – изгибающий момент
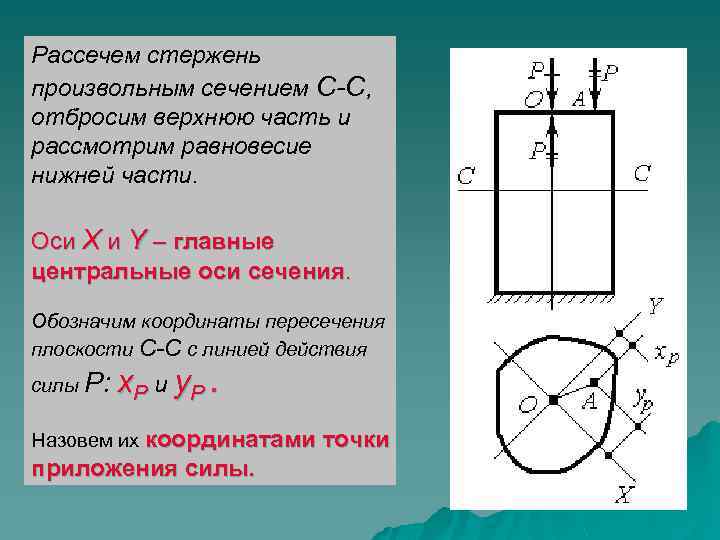
Рассечем стержень произвольным сечением С-С, отбросим верхнюю часть и рассмотрим равновесие нижней части. Оси Х и Y – главные центральные оси сечения. Обозначим координаты пересечения плоскости С-С с линией действия силы Р: x. Р и y. P. Назовем их координатами точки приложения силы.
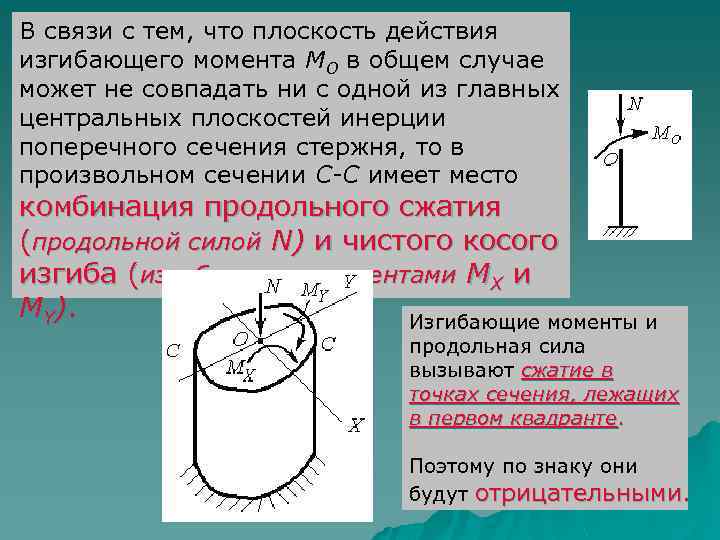
В связи с тем, что плоскость действия изгибающего момента МО в общем случае может не совпадать ни с одной из главных центральных плоскостей инерции поперечного сечения стержня, то в произвольном сечении С-С имеет место комбинация продольного сжатия (продольной силой N) и чистого косого изгиба (изгибающими моментами MX и M Y ). Изгибающие моменты и продольная сила вызывают сжатие в точках сечения, лежащих в первом квадранте. Поэтому по знаку они будут отрицательными.
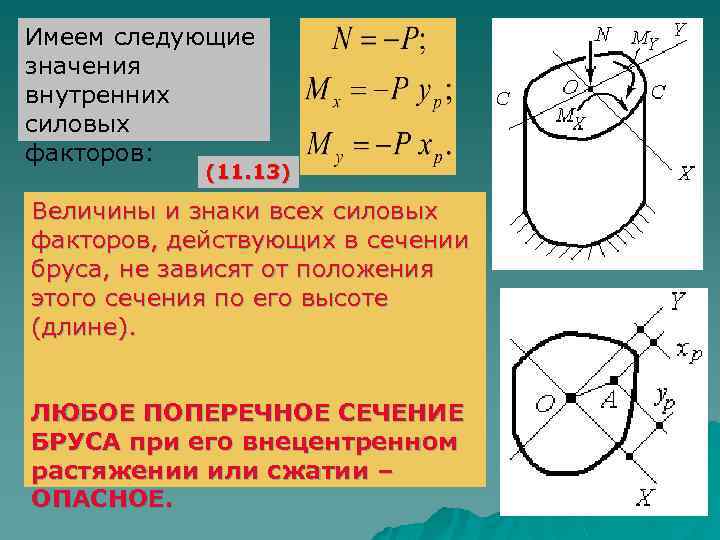
Имеем следующие значения внутренних силовых факторов: (11. 13) Величины и знаки всех силовых факторов, действующих в сечении бруса, не зависят от положения этого сечения по его высоте (длине). ЛЮБОЕ ПОПЕРЕЧНОЕ СЕЧЕНИЕ БРУСА при его внецентренном растяжении или сжатии – ОПАСНОЕ.
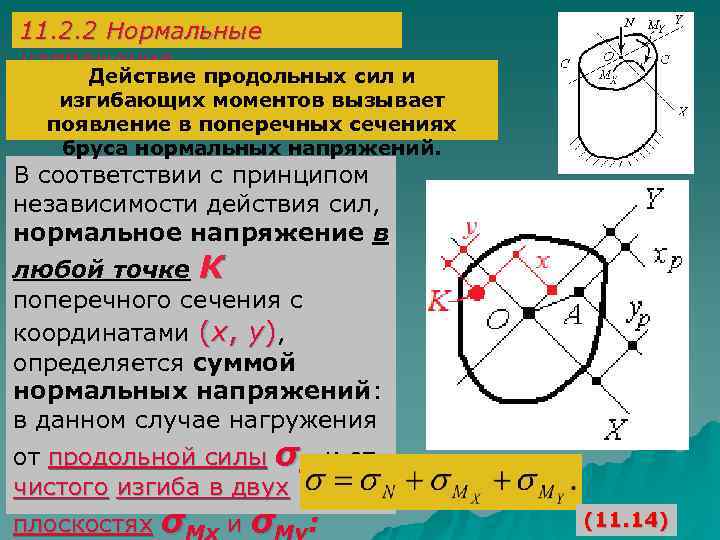
11. 2. 2 Нормальные напряжения Действие продольных сил и изгибающих моментов вызывает появление в поперечных сечениях бруса нормальных напряжений. В соответствии с принципом независимости действия сил, нормальное напряжение в любой точке К поперечного сечения с координатами (х, у), определяется суммой нормальных напряжений: в данном случае нагружения от продольной силы σN и от чистого изгиба в двух плоскостях σ иσ : (11. 14)

В соответствии с (11. 14): Для определения нормальных напряжений от действия рассматриваемых силовых факторов используем известные зависимости и получим: (11. 13) Окончательно: (11. 14) i. X и i. Y (11. 15) – радиусы инерции сечени

Легко видеть, что при изменении направления внешней силы, знак перед всеми слагаемыми в формуле (11. 14) силы изменится на плюс. Поэтому для того, чтобы по этой формуле получить правильный знак напряжений как при внецентренном сжатии, так и при внецентренном растяжении, нужно кроме знаков координат исследуемой точки сечения x и y, учесть знак приложенной внешней силы. При внецентренном растяжении перед всем выражением должен стоять знак плюс, при внецентренном сжатии – знак Формула для определения минус. нормальных напряжений при внецентренном растяжении или сжатии для любого направления внешней силы (11. 16)

11. 2. 3 Положение нейтральной линии Переменными в формуле являются два последних слагаемых, отражающих влияние изгиба. При изгибе наибольшие нормальные напряжения действуют в точках, наиболее удаленных от нейтральной оси. Следовательно, для определения опасных точек сечения необходимо определить положение нейтральной оси. Известно, что нормальные напряжения на нейтральной оси при изгибе равны нулю. Приравняем (11. 16) нулю: Обозначим координаты точек, принадлежащих нейтральной оси, х 0 и у 0.
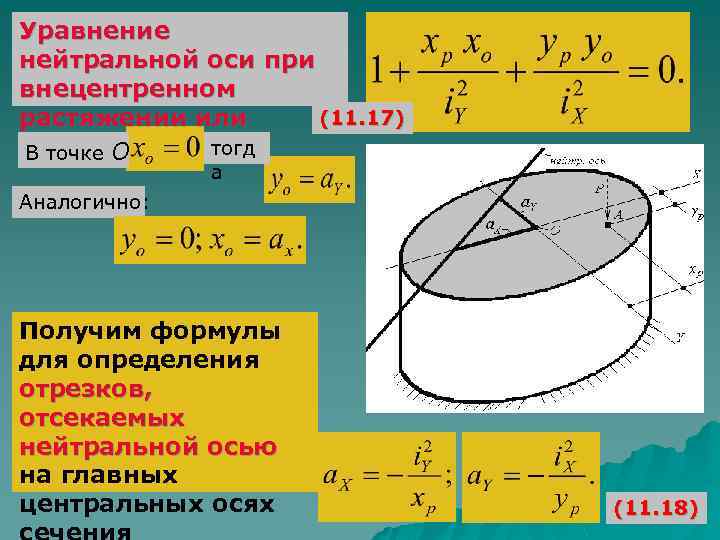
Уравнение нейтральной оси при внецентренном (11. 17) растяжении или сжатии: тогд В точке О а Аналогично: Получим формулы для определения отрезков, отсекаемых нейтральной осью на главных центральных осях (11. 18)
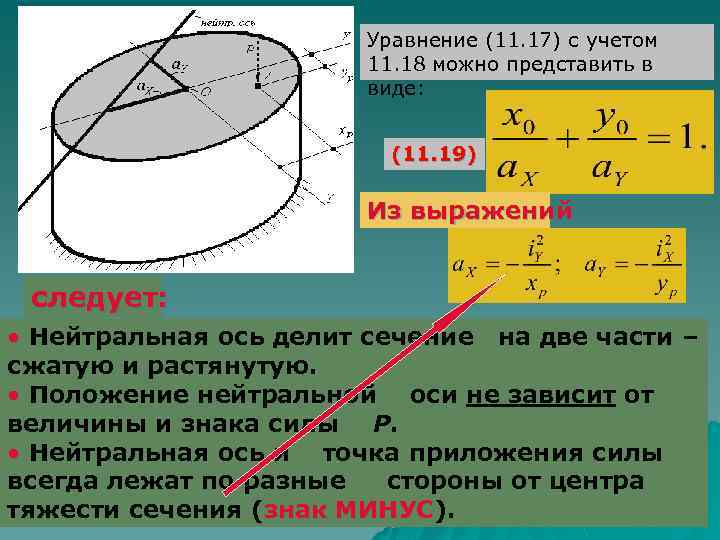
Уравнение (11. 17) с учетом 11. 18 можно представить в виде: (11. 19) Из выражений следует: • Нейтральная ось делит сечение на две части – сжатую и растянутую. • Положение нейтральной оси не зависит от величины и знака силы Р. • Нейтральная ось и точка приложения силы всегда лежат по разные стороны от центра тяжести сечения (знак МИНУС). МИНУС

• Если точка приложения силы расположена на одной из главных центральных осей инерции сечения, то нейтральная ось перпендикулярна к этой оси. Например: когда точка приложения силы расположена на оси X, то y. P = 0 и ay = ∞ , то нейтральная ось перпендикулярна оси X и параллельна оси Y. • Чем дальше от начала координат расположена точка приложения силы Р (чем больше x. P и y. P), тем ближе к центру тяжести сечения проходит нейтральная ось (тем меньше отрезки ax и ay) и наоборот.

11. 2. 4 Эпюра нормальных напряжений Рассмотрим произвольное поперечное сечение стержня, отложим значения отрезков a. X и a. Y, полученные по формулам (11. 18), и покажем положение нейтральной оси. К контуру сечения проведем касательные, параллельные нейтральной оси. Определим две точки D 1, которые наиболее удалены от нейтральной оси.
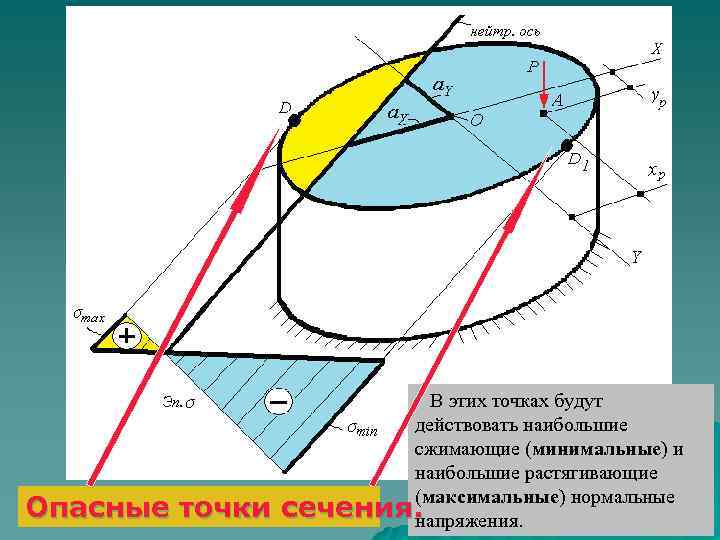
Опасные точки В этих точках будут действовать наибольшие сжимающие (минимальные) и наибольшие растягивающие (максимальные) нормальные сечения. напряжения.

11. 2. 5 Условие прочности составляется для опасных точек опасного сечения бруса. При составлении условия прочности необходимо учитывать геометрические особенности сечения и особенности поведения материалов в зависимости от знака напряжений. 1. Если сечение бруса имеет ОСЬ СИММЕТРИИ (прямоугольник, двутавр, швеллер), то определение опасных точек не вызывает затруднений. Экстремальные по величине нормальные напряжения возникают в волокне (в точке), где суммируются напряжения от всех внутренних силовых факторов (угловая точка сечения).

2. ХРУПКИЕ материалы плохо воспринимают действие растягивающих напряжений и достаточно хорошо – сжимающих (бетон и чугун). ПЛАСТИЧНЫЕ материалы безразличны к знаку напряжений. 3. Условие прочности для ПЛАСТИЧНОГО МАТЕРИАЛА записывается для максимальных по абсолютной величине напряжений. 3. 1. Для указанных в 1 пункте видов сечений: (11. 20)

3. 2. Для любого по форме поперечного сечения брус (11. 21) x и y – координаты точек сечения, наиболее удаленных от нейтральной оси. 4. Условие прочности для ХРУПКОГО МАТЕРИАЛА составляется в двух вариантах: 4. 1. Для волокон, где возникают максимальные по величине напряжения (11. 22)

4. 2. для волокон, где возникают минимальные по величине напряжения (11. 23) Каждое из значений сравнивается с соответствующим значением допускаемого напряжения. В формулы подставляются значения координат x и y точек сечения, наиболее удаленных от нейтральной оси, в которых возникают оси соответственно максимальные и минимальные напряжения. На основе составленного для заданных поперечного сечения и материала бруса условия (условий) прочности возможно решение трех типов задач: ПРОВЕРКА ПРОЧНОСТИ, ПРОЕКТИРОВОЧНЫЙ РАСЧЕТ, ОПРЕДЕЛЕНИЕ НЕСУЩЕЙ СПОСОБНОСТИ.
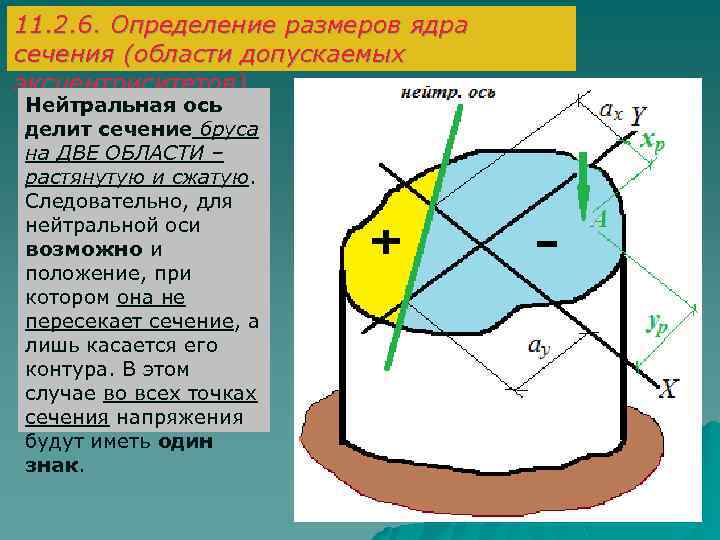
11. 2. 6. Определение размеров ядра сечения (области допускаемых эксцентриситетов) Нейтральная ось делит сечение бруса на ДВЕ ОБЛАСТИ – растянутую и сжатую. Следовательно, для нейтральной оси возможно и положение, при котором она не пересекает сечение, а лишь касается его контура. В этом случае во всех точках сечения напряжения будут иметь один знак.
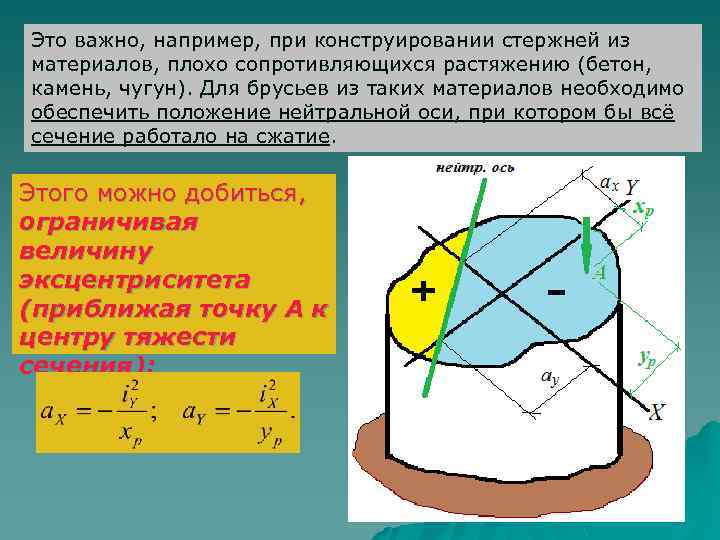
Это важно, например, при конструировании стержней из материалов, плохо сопротивляющихся растяжению (бетон, камень, чугун). Для брусьев из таких материалов необходимо обеспечить положение нейтральной оси, при котором бы всё сечение работало на сжатие. Этого можно добиться, ограничивая величину эксцентриситета (приближая точку А к центру тяжести сечения):
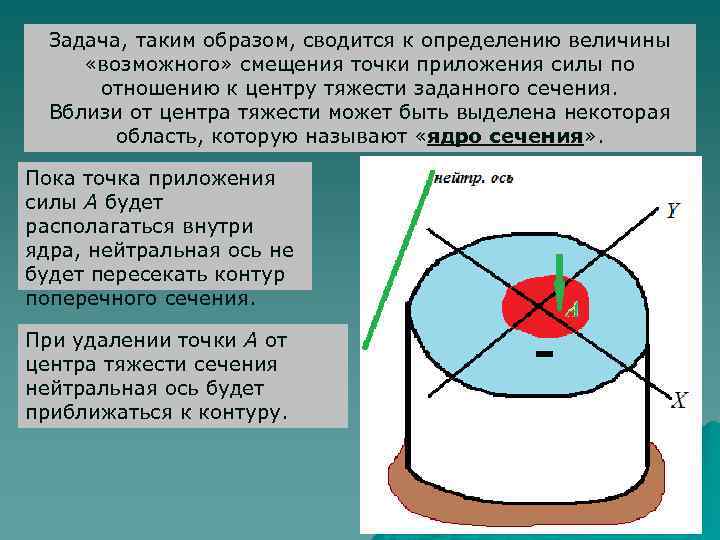
Задача, таким образом, сводится к определению величины «возможного» смещения точки приложения силы по отношению к центру тяжести заданного сечения. Вблизи от центра тяжести может быть выделена некоторая область, которую называют «ядро сечения» . Пока точка приложения силы А будет располагаться внутри ядра, нейтральная ось не будет пересекать контур поперечного сечения. При удалении точки А от центра тяжести сечения нейтральная ось будет приближаться к контуру.
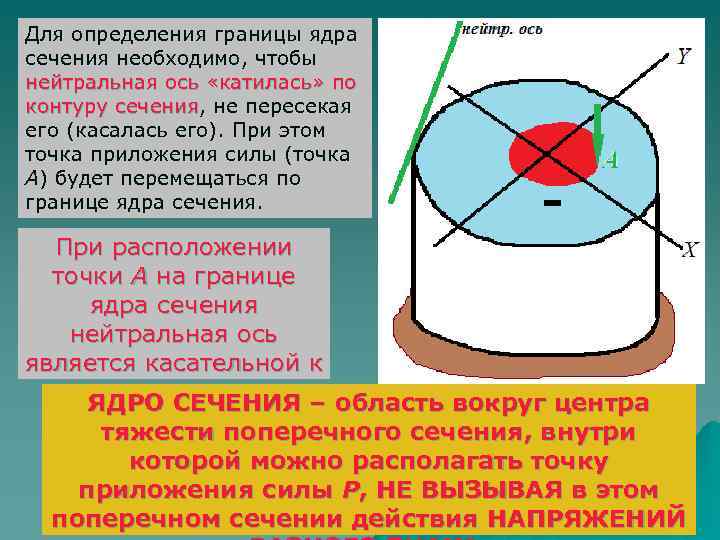
Для определения границы ядра сечения необходимо, чтобы нейтральная ось «катилась» по контуру сечения, не пересекая сечения его (касалась его). При этом точка приложения силы (точка А) будет перемещаться по границе ядра сечения. При расположении точки А на границе ядра сечения нейтральная ось является касательной к сечению. ЯДРО СЕЧЕНИЯ – область вокруг центра тяжести поперечного сечения, внутри которой можно располагать точку приложения силы Р, НЕ ВЫЗЫВАЯ в этом поперечном сечении действия НАПРЯЖЕНИЙ
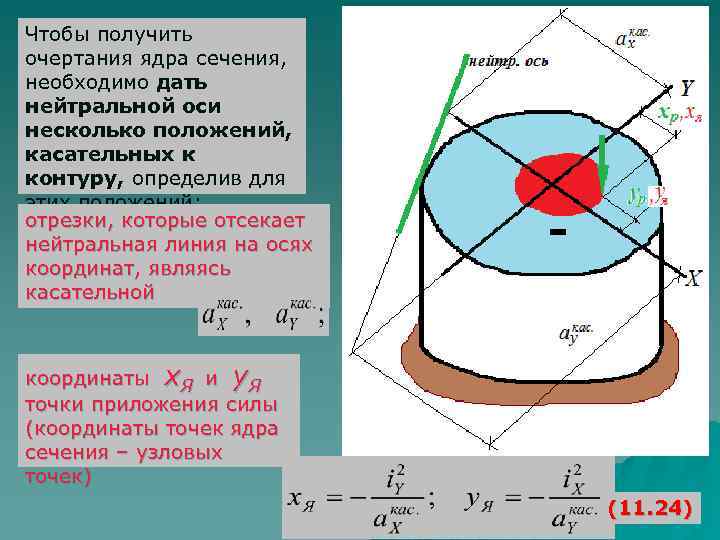
Чтобы получить очертания ядра сечения, необходимо дать нейтральной оси несколько положений, касательных к контуру, определив для этих положений: отрезки, которые отсекает нейтральная линия на осях координат, являясь касательной координаты х. Я и у. Я точки приложения силы (координаты точек ядра сечения – узловых точек) (11. 24)
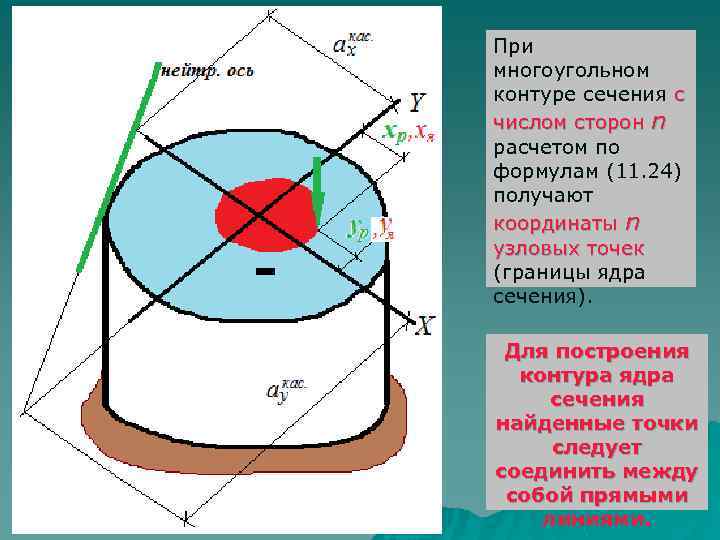
При многоугольном контуре сечения с числом сторон n расчетом по формулам (11. 24) получают координаты n узловых точек (границы ядра сечения). Для построения контура ядра сечения найденные точки следует соединить между собой прямыми линиями.

11. 2. 7. Примеры построения ядра сечения Круг диаметром d. Круг имеет две оси симметрии. Очевидно, что для построения ядра достаточно определить положение (величину отрезка и знак) одной точки, лежащей на контуре ядра сечения и, следовательно, достаточно провести одну касательную к контуру сечения. Касательная АВ отсекает на оси X отрезок на оси Y отрезок По формулам (11. 24) получаем: Ядро сечения круглого поперечного сечения – круг

Прямоугольник со сторонами b и h. Прямоугольник обладает двумя осями симметрии. Также очевидно, что в данном случае достаточно провести две касательные к контуру сечения и определить величину и знак двух отрезков на осях координат. Для касательной AB: Для касательной CD:
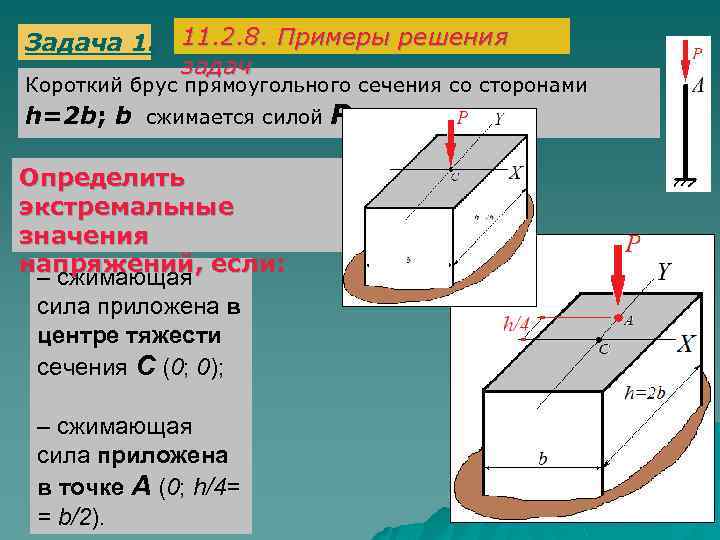
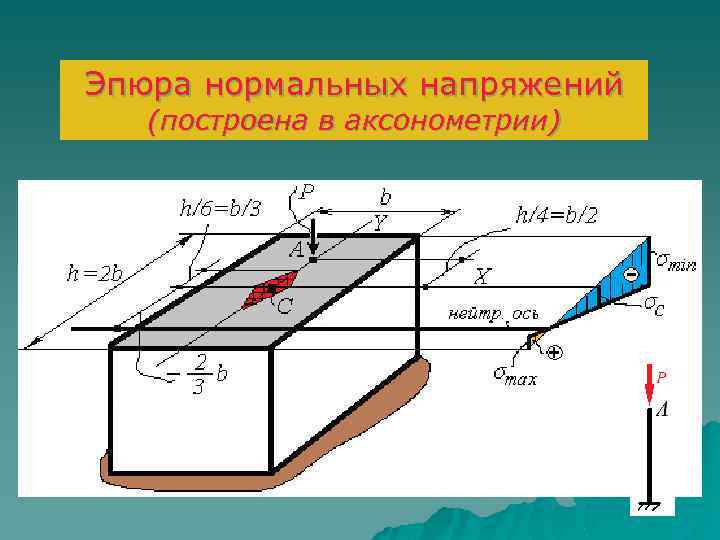
Задача 1. 11. 2. 8. Примеры решения задач Короткий брус прямоугольного сечения со сторонами h=2 b; b сжимается силой Р. Определить экстремальные значения напряжений, если: – сжимающая сила приложена в центре тяжести сечения С (0; 0); – сжимающая сила приложена в точке А (0; h/4= = b/2).
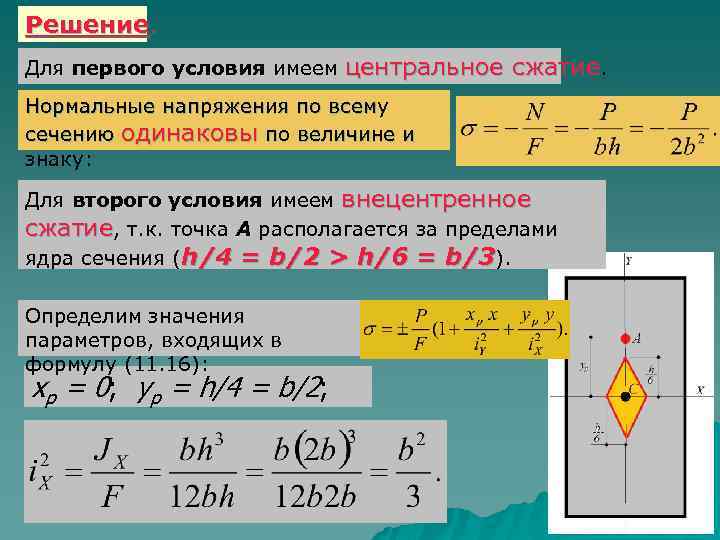
Решение. Для первого условия имеем центральное сжатие. Нормальные напряжения по всему сечению одинаковы по величине и знаку: Для второго условия имеем внецентренное сжатие, т. к. точка А располагается за пределами ядра сечения (h/4 = b/2 > h/6 = b/3). Определим значения параметров, входящих в формулу (11. 16): xp = 0; yp = h/4 = b/2;
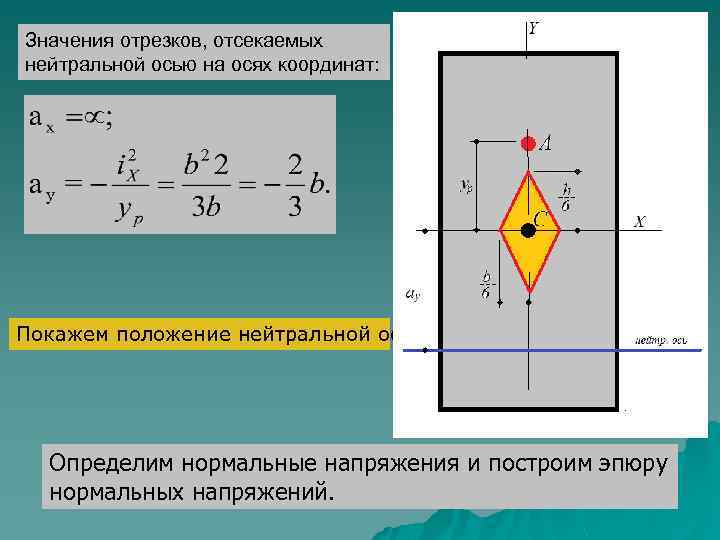
Значения отрезков, отсекаемых нейтральной осью на осях координат: Покажем положение нейтральной оси. Определим нормальные напряжения и построим эпюру нормальных напряжений.

Минимальные напряжения будут действовать в верхнем от нейтральной оси слое (y = h/2 = b): Максимальные напряжения будут действовать в нижнем от нейтральной оси слое (y = – h/2 = – b): Видим, что ошибка при монтаже (точка приложения силы за пределами центра тяжести и ядра сечения) приводит к увеличению сжимающих напряжений в 2, 5 раза.
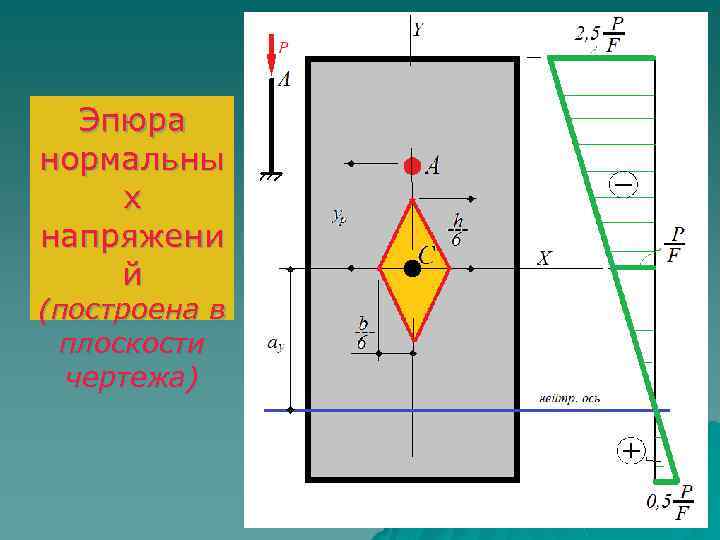
Эпюра нормальны х напряжени й (построена в плоскости чертежа)
Эпюра нормальных напряжений (построена в аксонометрии)
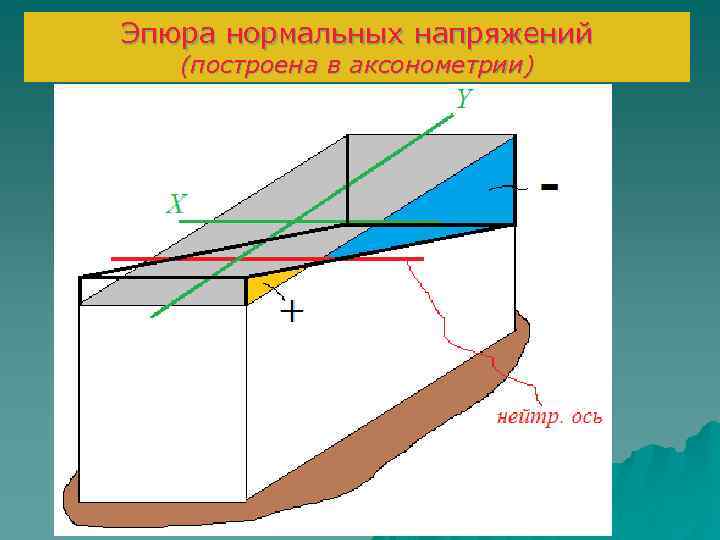
Эпюра нормальных напряжений (построена в аксонометрии)

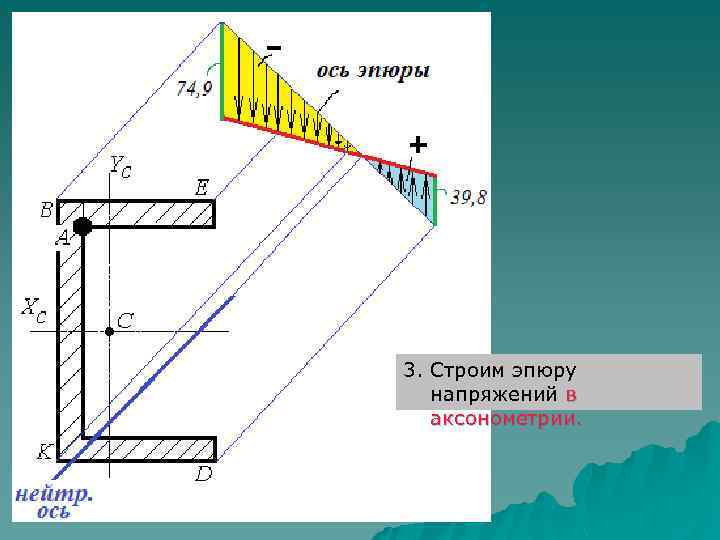
Задача 2. Проверить прочность короткой чугунной стойки, сжимаемой силой 200 к. Н, если допускаемые напряжения [σ]раст. = 40 МПа и [σ]сж = 100 МПа. Построить ядро сечения. 1) Положение центра сечения в Решение. системе координат X, Y:
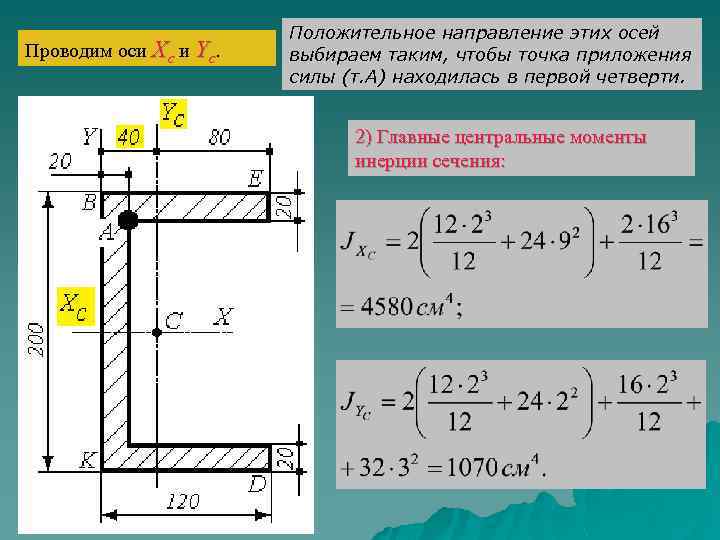
Проводим оси Хс и Yс. Положительное направление этих осей выбираем таким, чтобы точка приложения силы (т. А) находилась в первой четверти. 2) Главные центральные моменты инерции сечения:
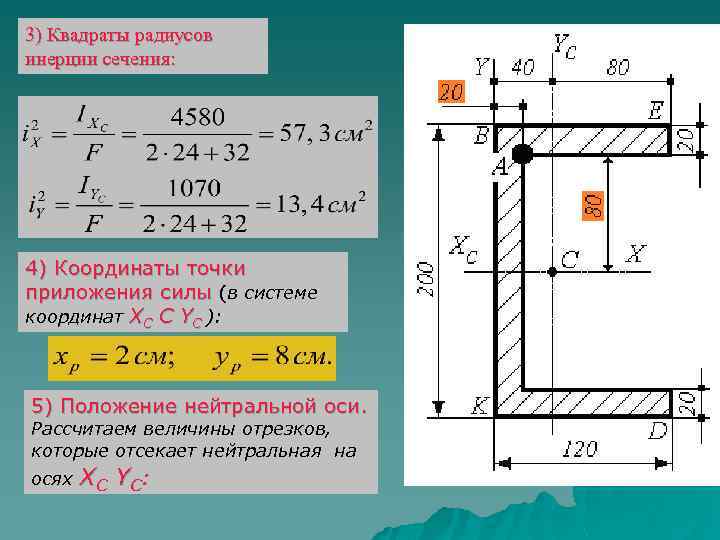
3) Квадраты радиусов инерции сечения: 4) Координаты точки приложения силы (в системе координат XС C YС ): 5) Положение нейтральной оси. Рассчитаем величины отрезков, которые отсекает нейтральная на осях XС Y С :
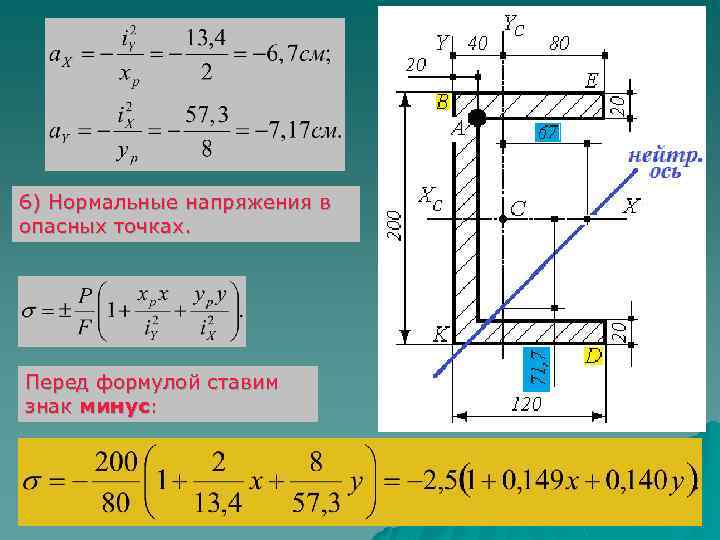
6) Нормальные напряжения в опасных точках. Перед формулой ставим знак минус:

Опасными являются точки сечения, наиболее удаленные от нейтральной оси (точки Координаты точек B и D: Подставляем эти координаты в формулу для нормальных напряжений. B и D).

3. Строим эпюру напряжений в аксонометрии.
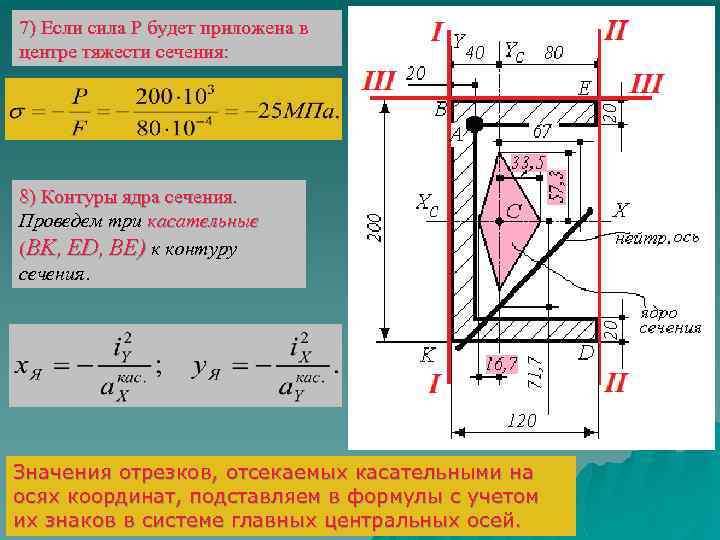
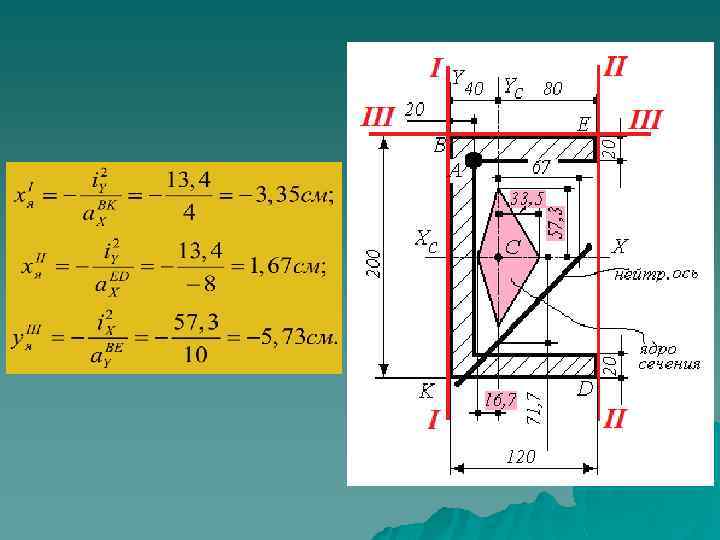
7) Если сила Р будет приложена в центре тяжести сечения: 8) Контуры ядра сечения. Проведем три касательные (BK, ED, BE) к контуру сечения. Значения отрезков, отсекаемых касательными на осях координат, подставляем в формулы с учетом их знаков в системе главных центральных осей.
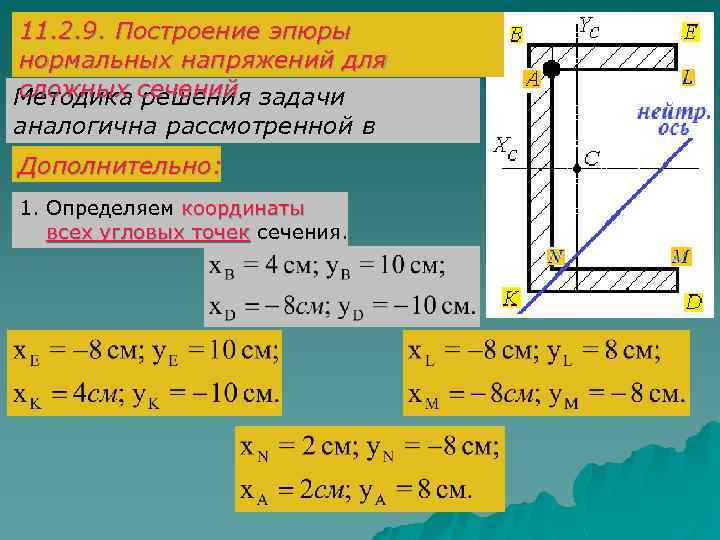
11. 2. 9. Построение эпюры нормальных напряжений для сложных решения Методика сечений задачи аналогична рассмотренной в примерах. Дополнительно: 1. Определяем координаты всех угловых точек сечения.
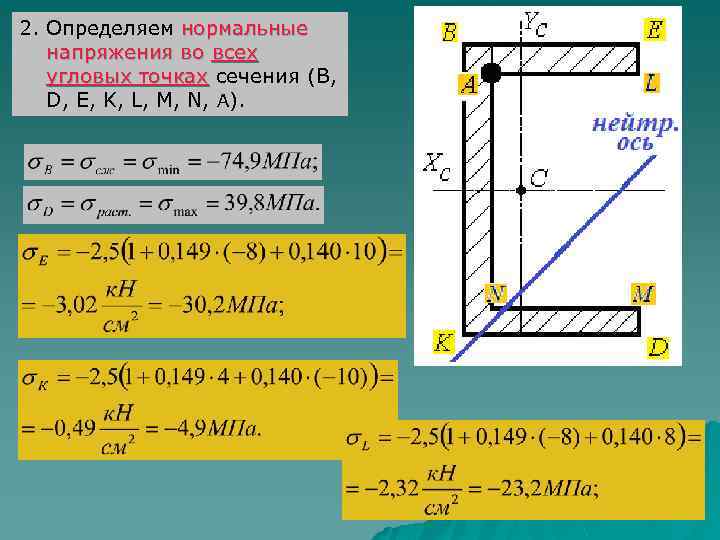
2. Определяем нормальные напряжения во всех угловых точках сечения (B, D, E, K, L, M, N, A).
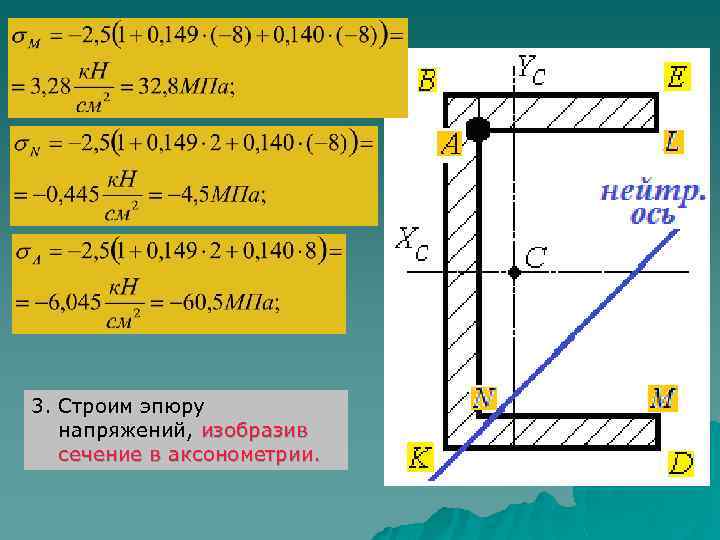
3. Строим эпюру напряжений, изобразив сечение в аксонометрии.
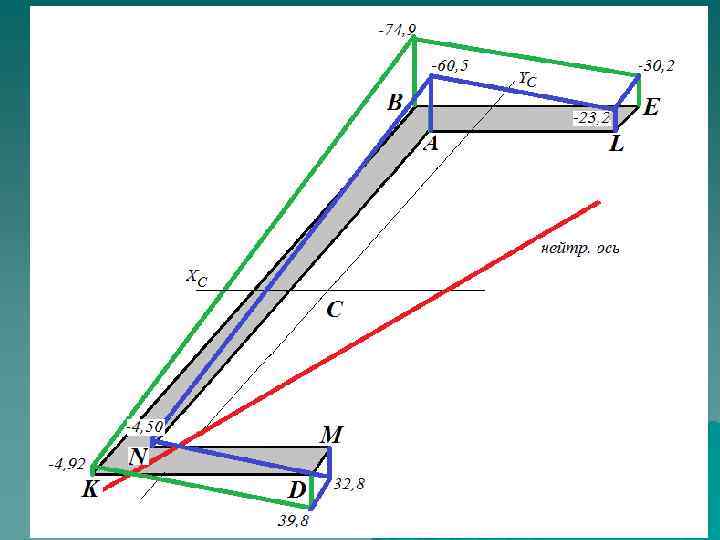
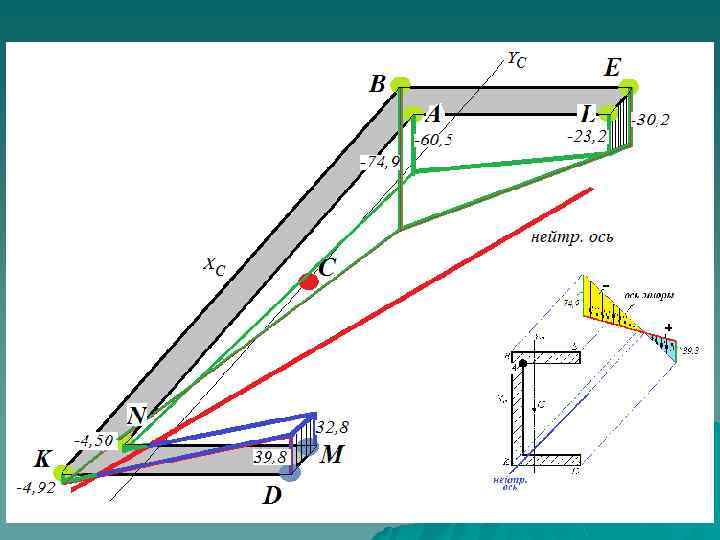
Источник
