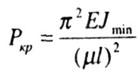Условие прочности при внецентренном растяжении или сжатии

Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения.
Косой изгиб.
Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса.
В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.

Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Условие прочности при косом изгибе:

где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси.
Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности:

где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей.
Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям.
Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей:

Изгиб с растяжением (сжатием).
При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M.
Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса:

К расчёту на прочность бруса при изгибе с растяжением:
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид:

Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле:

где А — площадь поперечного сечения.
Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле:

Условие прочночти имеет вид:

Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям.
Внецентренное растяжение или сжатие.
При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.

К расчёту на прочность бруса при внецентренном растяжении
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Приведём силу F к центру тяжести:

где уF , xF — координаты точки приложения силы F.
В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле:

Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:

Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.
Кручение с изгибом.
Сочетание деформаций изгиба и кручения характерно для работы валов машин.

Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения:

Эпюры напряжений в сечении бруса при кручении с изгибом
Нормальное напряжение достигает максимума на поверхности:

Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала:

Из третьей и четвёртой теории прочности:

При кручении с изгибом условие прочности имеет вид:

Источник
Многие элементы строительных конструкций (колонны, стойки, опоры) находятся под воздействием сжимающих сил, приложенных не в центре тяжести сечения. Рассмотрим, например, колонну, на которую опирается балка перекрытия (рис. 11.11). Поскольку сила Р, характеризующая передачу нагрузки от балки на колонну, действует по отношению к ее оси с эксцентриситетом е, колонна испытывает сжатие с изгибом. При этом в поперечных сечениях колонны наряду с продольной силой N = —Р возникает изгибающий момент, величина которого равна М = Ре.
Таким образом, внецентренное растяжение и сжатие стержня имеют место в случае, когда нагрузки действуют вдоль прямой, параллельной оси стержня. Будем рассматривать в основном задачи внецентренного сжатия, наиболее характерные для элементов строительных конструкций. При внецентренном растяжении во всех приводимых ниже формулах надо изменить знак перед силой Р на противоположный.
Рассмотрим стержень, нагруженный на торце внецентренно приложенной в точке К сжимающей силой Р, направленной параллельно оси Ох (рис. 11.12, а). Обозначим координаты точки приложения силы через ур и zp- Перенесем силу в центр тяжести сечения и согласно правилам статики добавим два момента Mz=—Pyp и Му = —Pzp (рис. 11.12, б). При этом внутренние усилия в произвольном поперечном сечении стержня будут равны:


Рис. 11.11

Рис. 11.12
Согласно принятому правилу знаков внутренние усилия являются отрицательными, поскольку в точках первой четверти сечения они вызывают сжатие. Отметим также, что величины внутренних усилий не изменяются по длине стержня и, таким образом, распределение нормальных напряжений в сечениях, достаточно удаленных от места приложения нагрузки, будет одинаковым.
Подставив (11.11) в (11.1), получим формулу для определения нормальных напряжений при внецентренном сжатии:

Эту формулу можно преобразовать к виду

где iy, iz — главные радиусы инерции сечения, определяемые по формулам:

Приравняв выражение (11.12) к нулю, получим уравнение нулевой линии

Полагая в этом уравнении последовательно у = 0 и z — 0, получим формулы для определения отрезков, отсекаемых нулевой линией на осях координат:

Отложив эти отрезки на осях, проведем нулевую линию (рис. 11.13), в каждой точке которой о = 0. Отметим, что при внецентренном сжатии (растяжении) нулевая линия не проходит через центр тяжести сечения, а ее положение не зависит от величины силы Р.
Поскольку знаки величин ^и^ противоположны знакам соответственно zp и у , нулевая линия проходит через те четверти системы координат, которые не содержат точки приложения силы (рис. 11.13).

Рис. 11.13
Рис. 11.14
Положение нулевой линии зависит от геометрических характеристик сечения и от координат точки приложения силы. При этом величины Zq, zp и у0, ^являются обратно пропорциональными по отношению друг к другу.
Исследуем изменение положения нулевой линии при перемещении точки приложения силы вдоль прямой, проходящей через центр тяжести сечения. Из формул (11.14) следует, что все нулевые линии будут при этом параллельными, причем при приближении точки приложения силы к центру тяжести сечения величины zp и у уменьшаются и нулевая линия удаляется от него, и наоборот (рис. 11.14).
Нетрудно доказать также следующее положение. Если точка приложения силы перемещается вдоль прямой, не проходящей через центр тяжести сечения, то нулевая линия поворачивается относительно некоторой точки (рис. 11.15). Справедливо и обратное утверждение. Это свойство используется при построении особой фигуры — ядра сечения.

Рис. 11.16
Рис. 11.15
Нормальные напряжения в сечении изменяются по линейному закону, увеличиваясь по абсолютной величине по мере удаления от нулевой линии. Эпюра о строится на прямой, перпендикулярной к нулевой линии. При этом она может быть разнозначной или однозначной (см. рис. 11.14). Последнее имеет место в случае, если точка приложения силы Р расположена вблизи центра тяжести сечения. Напомним, что при центральном сжатии или растяжении нормальные напряжения являются одинаковыми по величине, а эпюра с представляет собой прямоугольник.
В точках прямой, проходящей через центр тяжести сечения и параллельной нулевой линии, нормальные напряжения равны °о =—P/F.
Рассмотрим случай разнозначной эпюры с (рис. 11.14, а). Так же как и при косом изгибе, наибольшие растягивающие и сжимающие напряжения действуют в точках сечения, наиболее удаленных от нулевой линии (угловые точки А и В на рис. 11.14). Для произвольного сечения эти точки и их координаты устанавливаются с помощью касательных к сечению, параллельных нулевой линии (например, точка А на рис. 11.16). В общем случае онбф |онм|.
Если материал стержня неодинаково сопротивляется растяжению и сжатию, то необходимо обеспечить выполнение двух условий прочности по наибольшим растягивающим и наибольшим сжимающим напряжениям в точках А и В:

где Rp и Rc — расчетные сопротивления материала при растяжении и сжатии; zA, УА и zB, У в ~ координаты наиболее напряженных точек сечения.
Из условий прочности (11.15) можно определить величину предельной расчетной силы.
Для стержней из материала, одинаково сопротивляющегося растяжению и сжатию (R^ = Rc = R), а также в случае однозначной эпюры о (рис. 11.14, б) достаточно обеспечить выполнение одного условия прочности по точке с наибольшими по абсолютной величине напряжениями.
В инженерной практике чаще имеет место случай внецент- ренного сжатия (или растяжения), когда точка приложения силы Р расположена на одной из главных осей (рис. 11.17, а). При этом согласно формулам (11.14) нулевая линия параллельна другой главной оси (рис. 11.17, б). Нормальные напряжения определяются по двухчленной формуле. Например, для случая, показанного на рис. 11.17, имеем


Рис. 11.17
Многие строительные материалы (бетон, кирпичная кладка, чугун и др.) плохо сопротивляются растяжению. Поэтому в элементах конструкций из таких материалов, работающих на вне- центренное сжатие, нежелательно появление растягивающих нормальных напряжений. Это условие будет выполнено, если точка приложения силы расположена внутри или на границе некоторой области вокруг центра тяжести, которая называется ядром сечения.
Граница или контур ядра строится с помощью нулевых линий, которые являются касательными к сечению. При этом координаты точек контура ядра определяются с помощью формул
(11.14):

Здесь у0, Zq — координаты точек пересечения нулевых линий, касательных к контуру сечения, с осями координат; ур, zp — координаты точек контура ядра, соответствующие положению данной касательной.
Таким образом, если точка приложения силы расположена на контуре ядра, то нулевые линии являются касательными к сечению, а эпюра с представляет собой треугольник. При приложении силы внутри ядра нулевая линия проходит вне сечения (условная нулевая линия) и эпюра о является трапецией.
Ядро сечения содержит центр тяжести и является выпуклой фигурой, поскольку соответствующие границе ядра нулевые линии должны касаться огибающей контура сечения и не пересекать его.
При построении контура ядра его точки надо соединить соответствующими линиями. Если нулевые линии, касательные к сечению, перемещаются при переходе от одного положения к другому путем поворота вокруг угловых точек, то на основании изложенного выше положения линии контура ядра являются прямыми.

Рис. 11.18

Рис. 11.19

Рис. 11.20
Построим ядро сечения для некоторых фигур. Для прямоугольника достаточно провести две нулевые линии, являющиеся касательными к сечению (рис. 11.18). Для касательной 1 — 1 имеем у() = И/2 и Zq= °°. Учитывая, что

определяем координаты точки 1 контура ядра сечения:

Аналогично для касательной 2—2 находим координаты точки 2: zp = — b/6, ур = 0. Точки 3 и 4 расположены симметрично по отношению к точкам 1 и 2. Ядро сечения представляет собой ромб с длинами диагоналей h/З и Ь/3 (рис. 11.18).
Ядро сечения для двутавра также представляет собой ромб, значительно вытянутый вдоль оси Оу (рис. 11.19), поскольку J. » Jy. Ядро сечения для швеллера является четырехугольником, симметричным относительно оси Oz (рис. 11.20).
При построении ядра сечения для круга достаточно провести одну касательную 1—1 (рис. 11.21), для которой у0 = R, Zq = °°.

Рис. 11.21

Рис. 11.22
Учитывая, что для круга

находим координаты точки 1:

Очевидно, что ядро сечения для круга представляет собой также круг с радиусом г = R/4. Такой же вид имеет ядро для кольцевого сечения (рис. 11.22), однако радиус ядра значительно больше, чем для сплошного круга. Нетрудно показать, что при 5 « R2 радиус ядра сечения приближенно равен Rq/2, где Rq — средний радиус кольца.

Рис. 11.23
При построения ядра сечения, показанного на рис. 11.23, достаточно провести четыре касательные к сечению и определить координаты четырех точек контура ядра. Точки 1, 2 и 3 надо соединить прямыми линиями. Контур ядра между точками 3, 4 является криволинейным. Точки 5 и 6 симметричны по отношению к точкам 3 и 2.
Пример 11.5. Для короткого чугунного стержня коробчатого сечения, испытывающего внецентренное сжатие (рис. 11.24, а), определим расчетную величину силы Р из условий прочности. Построим эпюру о и ядро сечения. В расчетах примем Rp = = 50 МПа = 5 кН/см2, Rc = 150 МПа = 15 кН/см2 и ус = 1,0.

Рис. 11.24
Определяем необходимые геометрические характеристики сечения (рис. 11.24, б):

Координаты точки приложения силы Р равны: ур = 6 см, zp — = —4,5 см. Определяем по формулам (11.14) величины отрезков, отсекаемых нулевой линией на осях координат:

Отложив эти отрезки на осях, проводим нулевую линию, которая пересекает сечение и делит его на зоны растяжения и сжатия. Эпюра с является разнозначной (рис. 11.24, б). Наибольшие растягивающие и сжимающие напряжения действуют в угловых точках Ли В, наиболее удаленных от нулевой линии. Координаты этих точек равны: уА = —6 см, zA = 4,5 см, ув= 6 см, zB = —4,5 см.
Из условий прочности при растяжении и сжатии находим два значения расчетной силы Р:

Для обеспечения прочности стержня в зонах растяжения и сжатия принимаем с округлением меньшую силу Р = 100 кН. При этом напряжения в точках Ли В равны:

Прочность стержня обеспечена. Эпюра о приведена на рис. 11.24, б.
Для построения ядра сечения достаточно провести две нулевые линии, касательные к контуру сечения, и определить координаты двух точек контура ядра.
Касательная 1—1:

Касательная 2—2:

Проведенные касательные соответствуют точкам 1 и 2 контура ядра сечения. Симметрично расположены точки 3 и 4. Поскольку касательные переходят из одного положения в другое путем поворота вокруг угловых точек сечения, все линии контура ядра являются прямыми. Ядро сечения представляет собой ромб (рис. 11.24, б). Так как точка приложения силы принадлежит одновременно касательным 1—1 и 2—2 , нулевая линия проходит по линии контура ядра 1—2.
Пример 11.6. Для короткого стального стержня составного сечения, находящегося в условиях внецентренного сжатия (рис. 11.25, а), определим величину расчетной силы Риз условия прочности. В расчетах примем Р = 210МПа = 21 кН/см2 и ус = 0,9. Построим эпюру о и ядро сечения.
Поскольку zp = 0, данная задача относится к частному случаю внецентренного сжатия. Определяем необходимые геометрические характеристики сечения:

Определяем положение нулевой линии:


Рис. 11.25
Нулевая линия параллельна оси Oz и не пересекает сечение. Эпюра а является однозначной (рис. 11.25, б). Наибольшие сжимающие напряжения действуют в крайних верхних точках сечения (у = ув = —11 см). Из условия прочности определяем расчетное значение силы Р:

При действии силы Р = 744 кН наибольшие сжимающие напряжения в крайних верхних точках сечения по абсолютной величине равны уCR = 189 МПа. Определяем напряжения в крайних нижних точках сечения (у = уА= 11 см):

Напряжения в поперечных сечениях стержня являются сжимающими. Эпюра а приведена на рис. 11.25, б.
Ядро сечения представляет собой ромб, координаты вершин которого определяем с помощью двух касательных к сечению. Касательная 1—1:

Касательная 2—2:

Точка приложения силы расположена внутри ядра сечения (рис. 11.25, б).
Источник
Нормальные |
|
Р — равнодействующая |
F — площадь |
ХP, |
х, у — текущие |
ix, |
Рис. 7.2 |
Квадраты главных |
|
моменты инерции |
|
Так как Р # 0, |
|
Нулевая линия |
|
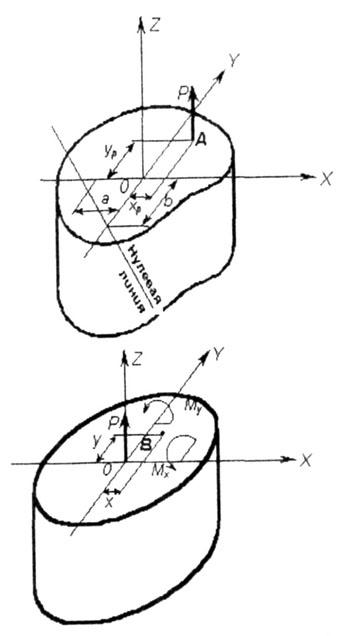
Центром |
(На рис. 7.2, а |
При проектировании |
Ядром |
Чтобы в поперечном |
Условияпрочности
при внецентренном растяжении-сжатии:
![]() ,
, ![]() .
.
32.Внецентренное сжатие коротких стержней. Определение положения нейтральной линии. Понятие о ядре сечения.
Нейтральная
линия при внецентренном растяжении
(сжатии) – это прямая, не проходящая
через центр тяжести сечения. Строить
эту прямую удобно с помощью отрезков
a0 и b0, отсекаемых на осях координат
(рис. 5.2.3.)
Формулы
для расчета этих отрезков имеют вид: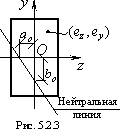
![]() (5.2.3)
(5.2.3)
В
этих формулах величины ey и ez , как
уже отмечалось, являются координатами
точки приложения силы F, т.е. берутся со
своими знаками.
Область
вокруг центра тяжести, внутри которой
приложение силы вызывает во всех точках
сечения напряжения одного знака,
называется ядром сечения. Для определения
ядра сечения необходимо задаться рядом
положений нейтральной линии, проводя
ее через граничные точки контура и
вычислить координаты точек приложения
силы ey и ez, используя формулы (5.2.3).
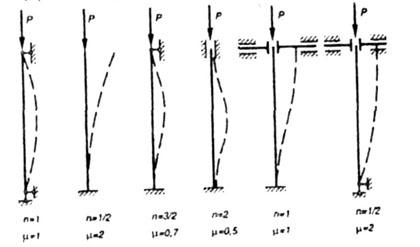
33.Расчет сжатых стержней на устойчивость . Определение критической силы. Формула л.Эйлера.
ОПРЕДЕЛЕНИЕ |
Для шарнирно |
|
где Е — модуль |
Jmin — |
Для стержней |
|
где |
|
Выражение |
Коэффициент |
|
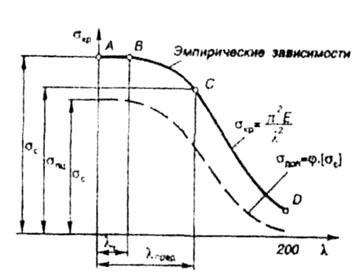
На рис. 8.2 |
|
Рис. 8.2 |
Формула Эйлера |
|
в свое время |
Применимость |
|
где |
|
|
Значение |
|
Предельная |
|
Так, для |
|
Для повышения |
верхней границей |
Следовательно, |
|
применима в |
|
(кривая СД на |
|
Рис. 8.3 |
Для малоуглеродистой |
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
10.02.20161.72 Mб11referat_turbaza.docx
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник

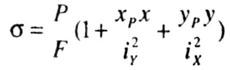
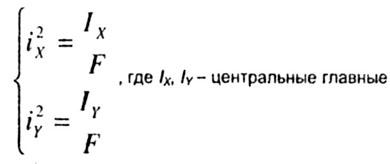
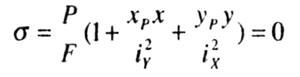
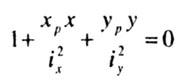
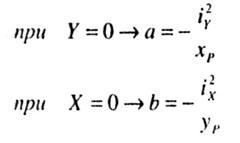
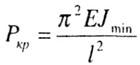
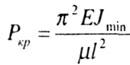
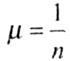
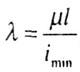
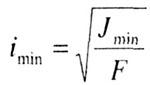 —
—