Условие прочности при растяжении сжатии записывается в виде

Министерство транспорта Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

Ульяновское высшее авиационное училище

Гражданской авиации (институт)

И.Н. Карпунина

Н.Ф. Леденева

И.А. Мельникова

И.Е. Сиднева

МЕХАНИКА

Методические указания
по выполнению расчетно-графических работ

(раздел «Сопротивление материалов»)

Ульяновск 2012

ББК В2

К 26

Карпунина, И. Н. Механика : метод. указания по выполнению расчетно-графических работ (раздел «Сопротивление материалов») / И. Н. Карпунина, Н. Ф. Леденева, И. А. Мель-никова, И. Е. Сиднева. – Ульяновск : УВАУ ГА(И), 2012. – 44 с.

Содержат задания и методические рекомендации по выполнению расчетно-графических работ по курсу «Механика» (раздел «Сопротивление материалов»). Для каждой темы приведены 30 вариантов схем, для каждой схемы – по 10 вариантов числовых значений.

Предназначены для курсантов направления 161000.62 – Аэронавигация, профилей подготовки 161000.62.08 – Поисковое и аварийно-спасательное обеспечение полетов воздушных судов и 161000.6209 – Обеспечение авиационной безопасности; для курсантов направления 280700.62 – Техносферная безопасность, профиля подготовки 280700.62.02 – Безопасность технологических процессов и производств.

Печатается по решению Редсовета института.

оглавление

1. Растяжение и сжатие. 4

1.1. Основные понятия. 4

1.2. Построение эпюр продольных сил, нормальных напряжений
и осевых перемещений. 6

1.3. Условие прочности при растяжении (сжатии) 8

1.4. Задание на расчетно-графическую работу № 1. 9

1.5. Пример выполнения расчетно-графической работы № 1. 9

1.6. Варианты расчетных схем.. 13

2. Сдвиг и кручение. 19

2.1. Основные понятия. 19

2.2. Задание на расчетно-графическую работу № 2. 20

2.3. Пример выполнения расчетно-графической работы № 2. 21

2.4. Варианты расчетных схем.. 24

3. Изгиб. 28

3.1. Основные понятия. 28

3.2. Задание на расчетно-графическую работу № 3. 30

3.3. Пример выполнения расчетно-графической работы № 3. 30

3.4. Варианты расчетных схем.. 34

Библиографический список. 42

РАСТЯЖЕНИЕ И СЖАТИЕ

Основные понятия

Растяжение (сжатие) – такой вид нагружения, при котором в поперечных сечениях бруса возникает только продольная сила N. При растяжении продольная сила направлена от сечения, при сжатии – к сечению.

На растяжение (сжатие) работают тросы, тяги приводов управления, шатуны, болты и многие другие детали.

Как показывает опыт, плоские поперечные сечения, перпендикулярные оси бруса, остаются плоскими и перпендикулярными к его оси при растяжении или сжатии (рис. 1.1). Это положение называют гипотезой плоских сечений. Из этой гипотезы следует, что напряжение во всех точках поперечного сечения одинаково, а значит, его можно найти как отношение внутренней силы N к площади поперечного сечения А.

Рис. 1.1

В поперечном сечении I–I при растяжении (сжатии) возникает только нормальное напряжение s, так как сила N перпендикулярна плоскости сечения:

. (1.1)

Под действием растягивающей силы (рис. 1.2) происходит удлинение бруса в продольном направлении и одновременное сужение в поперечном направлении.

Рис. 1.2

Абсолютное удлинение бруса:

. (1.2)

Относительное удлинение (относительная продольная деформация):

.(1.3)

Абсолютное сужение:

. (1.4)

Относительное сужение (относительная поперечная деформация):

. (1.5)

При растяжении абсолютная и относительная продольные деформации – величины положительные, поперечная деформация – величина отрицательная (так как ). При сжатии, наоборот, поперечная деформация – положительна, продольная – отрицательна.

Как показывает опыт, продольная и поперечная деформации связаны прямопропорциональной зависимостью:

, (1.6)

где m – коэффициент поперечной деформации (коэффициент Пуассона) – физическая постоянная материала, характеризующая его упругие свойства.

Величина коэффициента Пуассона определяется опытным путем. Его значения для разных материалов лежат в пределах . Для большинства сталей m = 0,3.

Для большинства материалов в определенных пределах справедлив закон Гука. Применительно к растяжению (сжатию) закон Гука формулируется так: нормальное напряжение при растяжении (сжатии) прямопропорционально относительной продольной деформации:

, (1.7)

где Е – модуль упругости (модуль Юнга) – физическая постоянная, характеризующая жесткость материала. Для сталей E = 2 × 105 МПа.

Подставим в формулу (1.7) зависимости для определения напряжения (1.1) и деформаций (1.3). Получим

откуда

. (1.8)

По формуле (1.8) определяют абсолютное удлинение (укорочение) бруса. Произведение EA называется жесткостью при растяжении (сжатии).

1.2. Построение эпюр продольных сил, нормальных напряжений
и осевых перемещений

Для проведения расчетов на прочность и жесткость необходимо знать, как изменяются продольные силы, нормальные напряжения и осевые перемещения по длине бруса. С этой целью строят специальные графики, называемые эпюрами. Рассмотрим построение эпюр на следующем примере.

Пусть ступенчатый брус с площадью поперечного сечения А в правой части и 2А – в левой нагружен осевыми силами F и 4F (рис. 1.3, а). Последовательность расчета бруса такова:

1. Разбиваем брус на участки, границами которых являются точки приложения сосредоточенных сил и места изменения поперечного сечения.

2. Методом сечений на каждом участке определяем продольную силу N. Расчет начинаем со свободного конца бруса. Разрежем третий участок произвольным поперечным сечением и отбросим левую часть. Покажем оставшуюся часть бруса и заменим действие отброшен-ной части продольной силой N3 (рис. 1.3, б).

Составляем уравнение равновесия:

, , .

Таким образом, третий участок испытывает сжатие ( ). По аналогии на втором и первом участках имеем

, ,

т. е. первые два участка испытывают растяжение.

Для построения эпюры продольных сил (рис. 1.3, д) проводим нулевую линию 0–0 параллельно оси бруса. Будем откладывать положительные величины вверх, а отрицательные – вниз от нулевой линии. На первом участке , т. е. первые два участка испытывают
растяжение. Поскольку сечение было сделано произ-вольно, можно утверждать, что в любом сечении на первом участке , т. е. эпюра имеет вид прямо-угольника, высота которого в выбранном масштабе равна силе 3F и отложена вверх от нулевой линии.

Рис. 1.3

По аналогии строится эпюра на втором и третьем участках.

3. Находим нормальное напряжение, возникающее в поперечных сечениях бруса на каждом участке:

На первом участке продольная сила N1 = 3F, площадь поперечного сечения – 2А, поэтому

На втором и третьем участках имеем

, .

Откладывая от нулевой линии найденные значения в масштабе, строим эпюру нормальных напряжений (рис. 1.3, е). Из эпюры видим, в частности, что максимальное напряжение возникает на втором участке.

4. Вычисляем осевые перемещения Δ. В заделке перемещение отсутствует (Δ = 0), поэтому расчеты начнем с заделки. В начале первого участка (z = 0) Δ0 = 0. В конце первого участка (z = 2a) перемещение будет равно удлинению бруса на этом участке, которое найдем по формуле (1.8):

В конце второго участка (z = 3a) перемещение будет складываться из перемещения правого конца первого участка и удлинения второго участка:

По аналогии на третьем участке (z = 4a):

В промежуточных точках участков перемещения определяются точками прямых, соединяющих значения Δ на границах участков, так как удлинение прямопропорционально расстоянию до сечения. С учетом этого строим эпюру осевых перемещений (рис. 1.3, ж). Из эпюры, в частности, видно, что свободный конец бруса переместится вправо (знак «+») на величину

Иногда производится расчет по условию жесткости, в соответствии с которым максимальное перемещение сравнивается с допускаемым значением осевого перемещения [Δ]: .

Условие прочности при растяжении (сжатии)

При расчете на прочность по допускаемым напряжениям считается, что прочность обеспечена, если максимальное возникающее в нем напряжение не превышает допускаемого напряжения, поэтому при растяжении (сжатии) условие прочности имеет следующий вид:

, (1.9)

здесь

или

где sТ – предел текучести; sВ– предел прочности; [n] – заданный запас прочности.

Условие прочности позволяет решать три типа задач:

1. Определение необходимых размеров поперечного сечения бруса.

Из неравенства (1.9) находится необходимая площадь поперечного сечения бруса:

Если сечение бруса – круг, то, зная площадь сечения, находят его диаметр; если сечение – прямоугольник, то по заданному соотношению сторон находят их размеры. Сечение бруса может быть стандартным профилем (уголок, двутавр, швеллер), в этом случае по найденной площади сечения находят соответствующий профиль по ГОСТам сортамента проката.

2. Определение безопасной нагрузки для бруса.

Из условия прочности (1.9) допустимое значение продольной силы, возникающей в брусе, удовлетворяет следующему условию:

По найденному значению Ν определяется и безопасная внешняя осевая нагрузка F. Если продольная сила постоянна по длине бруса, то F = Ν.

3. Проверка прочности бруса.

По заданным нагрузкам и размерам бруса определяется максимальное напряжение, возникающее в нем, и сравнивается с допустимым. Расхождение этих величин характеризует недогрузку или перегрузку бруса:

Рекомендуется, чтобы эта величина лежала в пределах ± 5 %.

Если материал бруса по-разному сопротивляется растяжению и сжатию, то проверку прочности ведут отдельно для растянутых и сжатых участков:

, .

Задание на расчетно-графическую работу № 1

Расчетно-графическая работа № 1 по теме «Растяжение и сжатие» включает две задачи: подбор сечений статически определимого бруса из хрупкого материала (чугуна) и определение безопасной нагрузки для статически определимого бруса.

Задача 1. Для чугунного бруса построить эпюру продольных сил. Из расчета на прочность подобрать размеры круглого и квадратного поперечных сечений участков бруса.

Вариант	I	II	III	IV	V	VI	VII	VIII	IX	X
F, кH
sВР, МПа
sВС, МПа
[n]	2,5	3,0	3,5	4,0	3,5	2,5	3,0	3,5	4,0	3,5

Варианты расчетных схем к задаче 1 приведены на с. 13–15.

Задача 2. Для стального бруса построить эпюры продольных сил, нормальных напряжений и осевых перемещений. Из расчета на прочность по допускаемым напряжениям определить безопасное значение силы F. Вычислить перемещение точки приложения этой силы.

Вариант	I	II	III	IV	V	VI	VII	VIII	IX	X
A, мм2
l, мм
[s], МПа

Варианты расчетных схем к задаче 2 приведены на с. 16–18.

Дата добавления: 2017-02-11; просмотров: 3407 | Нарушение авторских прав | Изречения для студентов

1. Зависимость,
выражающая закон Гука

1)
;

1. Для пластичных материалов
считается опасным напряжение

1)
;

2.
При продольном растяжении диаметр образца увеличили в 2
раза. При этом прочность

1) увеличится в 4 раза;

3.
Условие прочности при растяжении (сжатии)
записывается в виде

1) ;

4.
Условие жесткости при растяжении (сжатии)записывается
в виде

1)
;

6. К упругим постоянным свойствам
материала относятся

1) .

7. При
испытании на растяжение диаметр и длину образца увеличили в 2 раза, при этом
удлинение

1) уменьшится в 2 раза;

8. Сечение при растяжении (сжатии) является опасным, когда

1) возникают по модулю
наибольшие нормальные напряжения;

9. Условие
прочности при кручении

1) ;

10.
Если диаметр вала увеличить в 2 раза, то допускаемый крутящий момент

1) увеличится в 8 раз.

1.
При кручении является опасным сечение вала, в
котором

1) возникают максимальные касательные напряжения;

12. Система называется статически
неопределимой, если

1) для её решения недостаточны только уравнения статики;

13.
Условие прочности при изгибе

1)
.

14. При одинаковой площади сечений
более прочным при изгибе балки является

1) двутавровое;

15.
Высота балки — h, ширина
– b; h = 2b.
Если балку повернуть на 90°, то прочность при изгибе измениться

1) в 2 раза;

16.
При косом изгибе

1) изгибающий момент не совпадает ни с одной главной осью
инерции.

17.
Валы редукторов, как правило, испытывают деформации

1) изгиба и кручения;

18. Ядром сечения называется

1) область вокруг центра тяжести, при приложении в
которой продольной силы, в сечении возникают напряжения одинакового знака;

19. Стержень, у которого μ = 1, изображен на
рисунке

Условие прочности при растяжении сжатии записывается в виде

20.
По III теории прочности при
деформации изгиба с кручением эквивалентное напряжение определяется по формуле:

1) ;

21. При расположении продольной сжимающей
силы вне центра тяжести бруса возникает состояние, называемое

1) внецентренным сжатием;

22. Динамический коэффициент при ударной
нагрузке определяется по формуле

23. Стержень АВ испытывает деформацию

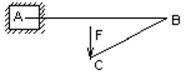
Условие прочности при растяжении сжатии записывается в виде

1) изгиба с кручением.

24.Гибкость стержня при
продольном изгибе зависит от

1) формы, размеров и способа закрепления стержня;

25.Потеря
устойчивости стержня происходит при превышении напряжения

1) критического значения;

26.Динамическое напряжение при ударе можно уменьшить,

1) используя балку на упругой опоре;

27.Пределом выносливости называется

1) наибольшее напряжение цикла, при котором не происходит
разрушения до базы испытания;

28.При
переменных нагрузках лучше использовать резьбы с шагом

1) мелким;

29.
Крепежные резьбы,
в основном, выполняют с профилем

1) треугольным;

30.
При
одинаковых параметрах меньшими габаритами обладает передача

1) зубчатая;

31.Основным критерием работоспособности
соединений является

1) прочность;

32. Проектный расчет закрытых зубчатых передач
выполняют, как правило, по

1) контактным напряжениям;

33. Условие прочности болта, когда он затянут, а
внешняя нагрузка отсутствует, определяется выражением

1) ;

34.Угловые швы рассчитывают по

1) касательным напряжениям относительно сечения по
биссектрисе прямого угла шва.

35.Шпоночные соединения обычно рассчитывают по
напряжениям

1) смятия;

36.При проектном
расчете по напряжениям изгиба вычисляется

1) модуль;

37. Для изготовления червячных колес при
скоростях скольжения, больших 5 м/с, рекомендуют
использовать

1) оловянную бронзу;

38.Передача усилия в ременной передаче
происходит за счет

1) сил трения между шкивами и ремнем, вследствие
натяжения;

39.Тяговая способность ременной передачи
характеризуется:

1) значением максимально допустимой окружной силы Ft
или полезного напряжения τt;

40.Проектный расчет цепной передачи выполняют по

1) износостойкости шарниров.

41.
Шатун
двигателя внутреннего сгорания совершает движение

1) плоско — параллельное;

42. При значительных передаточных числах в
одноступенчатом редукторе применяется передача

1) червячная;

43.В механизмах коромысло совершает движение

1) неполное вращательное;

44.В состав механизма входит тело, которое называют

1) звеном;

45.Звено в механизме, закон движения которого
задан, называется

1) начальным звеном;

46.Кинематическая пара II класса имеет количество звеньев, равное

1) 2;

47.Для закрепления деталей на осях и валах
служат соединения

1) все ответы, кроме первого, верны.

48.
Эпюры
изгибающих моментов строятся для:

1) определения опасного сечения;

2) определения перемещений графоаналитическим способом.

49. Когда внешняя нагрузка раскрывает стык
деталей резьбового соединения, расчет ведут по условию:

1) отсутствия сдвига деталей в стыке;

2) нераскрытия стыка.

50.Преимущества косозубого зацепления
обусловлены:

1) увеличением суммарной длины контактной линии;

2) плавностью зацепления.

51.Мелкомодульные зубчатые колеса
предпочтительны по условиям:

1) плавности хода;

2) экономичности;

52.Заклепки испытывают следующие виды
деформации:

1) смятие;

2) сдвиг;

53.Контактные напряжения в зубчатой передаче
зависят от:

1) диаметра колес;

2) ширины зубчатых колес.

54.Подшипники качения рассчитываются:

1) на статическую грузоподъемность;

2) на ресурс (долговечность) по усталостному
выкрашиванию;

55.
Перемещением
при изгибе называется

1) прогиб и угол поворота балки;

2) прогиб балки;

3) угол поворота балки;

56.Преимущества сварных соединений в следующем:

1) составные детали приближены к цельным,
равнопрочность элементов;

2) низкий расход материала;

3) низкая стоимость изделия.

57.К повреждениям поверхности зубьев относятся:

1) усталостное выкрашивание;

2) абразивный износ;

3) пластические сдвиги.

58.При высоких температурах нагрева масла в
редукторе:

1) обдувают корпус воздухом;

2) устраивают водяные рубашки или змеевики;

3) применяют циркуляционные системы смазки со специальным
холодильником;

59.Большую тяговую способность обеспечивают
ремни:

1) клиновые;

2) поликлиновые;

3) зубчатые.

60.Механические муфты предназначены для:

1) соединения концов вала, стержней, труб;

2) снижения перекосов валов;

3) предохранения машины от перегрузок.

УСТАНОВИТЕ СООТВЕТСТВИЕ

61. Установите соответствие между принципом действия и видом механической
передачи

Принцип действия	Вид механической передачи
1) трение	б) ременная
2) зацепление	а) цепная

62. Установите соответствие между видом
деформации и характеристикой
прочности сечения

Вид деформации	Характеристика прочности сечения
1) растяжение – сжатие	г) площадь
2) кручение	б) полярный момент сопротивления
3) изгиб	а) осевой момент сопротивления

63. Установите соответствие между видом
деформации и характеристикой
жесткости сечения

Вид деформации	Характеристика прочности сечения
1) растяжение – сжатие	г) площадь
2) кручение	в) полярный момент инерции
3) изгиб	д) осевой момент площади

УСТАНОВИТЕ ПРАВИЛЬНУЮ ПОСЛЕДОВАТЕЛЬНОСТЬ

64. Передачи в приводе рекомендуют
располагать в последовательности:

1)
ременная.

2)
зубчатая или червячная (редуктор);

3)
цепная;

65. Расчет клиноременной передачи
выполняют в последовательности:

1) выбирают сечение ремня и диаметры шкивов;

2) назначают межосевое расстояние и выбирают длину
ремня.

3) определяют мощность, передаваемую одним ремнем в
условиях
эксплуатации;

4) определяют число ремней;

5)определяют силу предварительного натяжения одного
ремня;

6) вычисляют силу, действующую на вал;

66. Расчет закрытой зубчатой передачи
выполняют в последовательности:

1)выбор материала и определение допускаемых напряжений.

2)проектный расчет передачи;

3)расчет геометрических параметров;

4)проверка зубьев по контактным напряжениям;

5)проверка зубьев по напряжениям изгиба;

ДОПОЛНИТЕ

67. Отношение делительного окружного
шага зубьев прямозубой цилиндрической передачи к числу π называется модуль.

68. Часть опоры вала, передающая опорной
части усилия от вала и обеспечивающая определенный режим вращения, называется подшипник.

69. Наибольшее напряжение, до
которого материал следует закону Гука, называется предел пропорциональности.

70. Способность элементов конструкции
сохранять исходную форму упругого    равновесия
   при
   воздействии    внешних    нагрузок   называется устойчивость.

Источник

Условие прочности при растяжении сжатии записывается в виде

1. Зависимость, выражающая закон Гука

3. Условие прочности при растяжении (сжатии) записывается в виде

6. К упругим постоянным свойствам материала относятся

8. Сечение при растяжении (сжатии) является опасным, когда

10. Если диаметр вала увеличить в 2 раза, то допускаемый крутящий момент

1. При кручении является опасным сечение вала, в котором

12. Система называется статически неопределимой, если

14. При одинаковой площади сечений более прочным при изгибе балки является

16. При косом изгибе

18. Ядром сечения называется

29. Крепежные резьбы, в основном, выполняют с профилем

30. При одинаковых параметрах меньшими габаритами обладает передача

41. Шатун двигателя внутреннего сгорания совершает движение

48. Эпюры изгибающих моментов строятся для:

55. Перемещением при изгибе называется

1. Зависимость,
выражающая закон Гука

3.
Условие прочности при растяжении (сжатии)
записывается в виде

6. К упругим постоянным свойствам
материала относятся

10.
Если диаметр вала увеличить в 2 раза, то допускаемый крутящий момент

1.
При кручении является опасным сечение вала, в
котором

12. Система называется статически
неопределимой, если

14. При одинаковой площади сечений
более прочным при изгибе балки является

16.
При косом изгибе

29.
Крепежные резьбы,
в основном, выполняют с профилем

30.
При
одинаковых параметрах меньшими габаритами обладает передача

41.
Шатун
двигателя внутреннего сгорания совершает движение

48.
Эпюры
изгибающих моментов строятся для:

55.
Перемещением
при изгибе называется