Условие прочности при кручении с растяжением

Эта статья будет посвящена расчетам на прочность, которые выполняются в сопромате и не только. Расчеты на прочность бывают двух видов: проверочные и проектировочные (проектные).
Проверочные расчеты на прочность – это такие расчеты, в ходе которых проверятся прочность элемента заданной формы и размеров, под некоторой нагрузкой.
В ходе проектировочных расчетов на прочность определяются какие-то размеры элемента из условия прочности. Причем, очевидно, что для разных видов деформаций эти условия прочности различны. Также к проектным расчетам можно отнести расчеты на грузоподъемность, когда вычисляется максимальная нагрузка, которую может выдерживать конструкция, не разрушаясь. Рассмотрим более подробно, как проводится прочностные расчеты для разных случаев.
Расчеты на прочность при растяжении (сжатии)
Начнем, пожалуй, с самого простого вида деформации растяжения (сжатия). Напряжение при центральном растяжении (сжатии) можно получить, разделив продольную силу на площадь поперечного сечения, а условие прочности выглядит вот так:

где сигма в квадратных скобках – это допустимое напряжение. Которое можно получить, разделив предельное напряжения на коэффициент запаса прочности:

Причем, за предельное напряжение для разных материалов принимают разное значение. Для пластичных материалов, например, для малоуглеродистой стали (Ст2, Ст3) принимают предел текучести, а для хрупких (бетон, чугун) берут в качестве предельного напряжения – предел прочности (временное сопротивление). Эти характеристики получают при испытании образцов на растяжение или сжатие на специальных машинах, которые фиксируют характеристики в виде диаграммы.

Коэффициент запаса прочности выбирается конструктором исходя из своего личного опыта, назначения проектируемой детали и сферы применения. Обычно, он варьируется от 2 до 6.
В случае если необходимо подобрать размеры сечения, площадь выражают таким образом:

Таким образом, минимальная площадь поперечного сечения при центральном растяжении (сжатии) будет равна отношению продольно силы к допустимому напряжению.
Расчеты на прочность при кручении
При кручении расчеты на прочность в принципе схожи с теми, что проводятся при растяжении. Только здесь вместо нормальных напряжений появляются касательные напряжения.
На кручение работают, чаще всего, детали, которые называются валами. Их назначение заключается в передаче крутящего момента от одного элемента к другому. При этом вал по всей длине имеет круглое поперечное сечение. Условие прочности для круглого поперечного сечения можно записать так:

где Ip — полярный момент сопротивления, ρ — радиус круга. Причем по этой формуле можно определить касательное напряжение в любой точке сечения, варьируя значение ρ. Касательные напряжения распределены неравномерно по сечению, их максимальное значение находится в наиболее удаленных точках сечения:

Условие прочности, можно записать несколько проще, используя такую геометрическую характеристику как момент сопротивления:

То бишь максимальные касательные напряжения равны отношению крутящего момента к полярному моменту сопротивления и должны быть меньше либо равны допустимому напряжению. Геометрические характеристики для круга, упомянутые выше можно найти вот так:

Иногда в задачах встречаются и прямоугольные сечения, для которых момент сопротивления определяется несколько сложнее, но об этом я расскажу в другой статье.
Расчеты на прочность при изгибе

Источник
Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения.
Косой изгиб.
Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса.
В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.

Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Условие прочности при косом изгибе:

где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси.
Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности:

где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей.
Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям.
Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей:

Изгиб с растяжением (сжатием).
При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M.
Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса:

К расчёту на прочность бруса при изгибе с растяжением:
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид:

Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле:

где А — площадь поперечного сечения.
Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле:

Условие прочночти имеет вид:

Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям.
Внецентренное растяжение или сжатие.
При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.

К расчёту на прочность бруса при внецентренном растяжении
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Приведём силу F к центру тяжести:

где уF , xF — координаты точки приложения силы F.
В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле:

Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:

Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.
Кручение с изгибом.
Сочетание деформаций изгиба и кручения характерно для работы валов машин.

Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения:

Эпюры напряжений в сечении бруса при кручении с изгибом
Нормальное напряжение достигает максимума на поверхности:

Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала:

Из третьей и четвёртой теории прочности:

При кручении с изгибом условие прочности имеет вид:

Источник
Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.
Брусья, испытывающие кручение, принято называть валами.
Внутренний крутящий момент
Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.
Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.
Величина крутящего момента в любом сечении вала определяется методом сечений: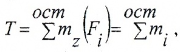
т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.
Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.
В технике наиболее широко используются валы круглого поперечного сечения.
Теория кручения круглых валов основана на следующих гипотезах:
- поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
- радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.
Напряжения при кручении
В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле: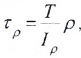
где Iρ — полярный момент инерции.
Эпюра касательных напряжений при кручении имеет следующий вид: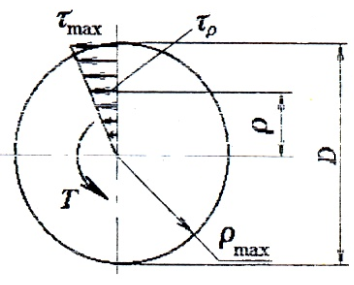
Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρmax: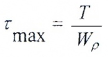
Здесь: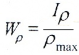
— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала: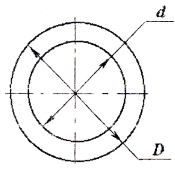
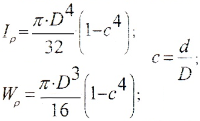
б) для вала сплошного сечения (c=0)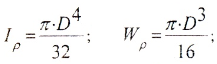
в) для тонкостенной трубы (t0,9)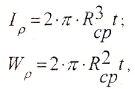
где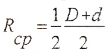
— радиус срединной поверхности трубы.
Деформации
Деформации валов при кручении заключаются в повороте одного сечения относительно другого.
Угол закручивания вала на длине Z определяется по формуле: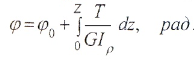
Если крутящий момент и величина GIρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем: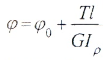
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания: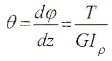
Расчет валов сводится к одновременному выполнению двух условий:
- условию прочности:
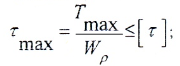
- условию жесткости:
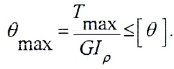
Для стальных валов принимается:
Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:
- проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
- Проектировочный расчет, при котором вычисляются диаметры:
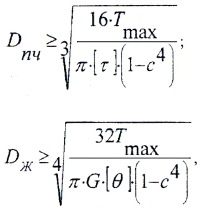
при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ. - Определение грузоподъемности вала:
Из двух найденных значений крутящего момента необходимо принять меньшее.
При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.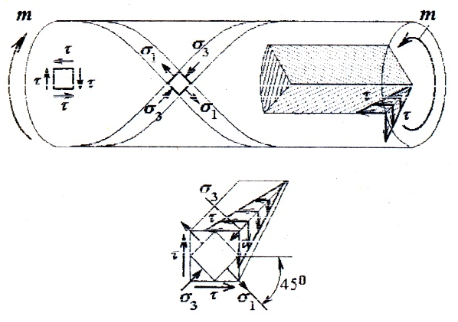
Главные напряжения σ1 = τ, σ3 = -τ наклонены под углом α=±45о к образующей.
Потенциальная энергия упругой деформации определяется по формуле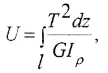
или для участка вала при постоянном T и GIρ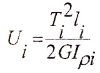
Лекции по сопромату >
Примеры решения задач >
Источник
Сопротивление материалов
Деформация кручения
Расчеты на прочность и жесткость при кручении
Условие прочности бруса при кручении заключается в том, что наибольшее касательное напряжение, возникающее в нем, не должно превышать предельно допустимое. При этом расчетная формула на прочность имеет вид:
τmax = Мкр / Wr≤ [τкр],
где [τкр] — предельное допускаемое напряжение.
При практических расчетах, определяя предельные допускаемые напряжения для различных материалов, используют зависимость между напряжениями при растяжении и напряжениями при кручении, которая для стали и чугуна имеет вид:
для стали — [τкр] = 0,55….0,6 [σр]
для чугуна — [τкр] = 1,0….1,2 [σр])
(здесь [σр] — справочная или определяемая экспериментально величина, (предельное допустимое напряжение растяжения) характеризующая материал бруса (вала).
Кроме требования прочности к валам предъявляются требования жесткости, которое заключается в том, что угол закручивания участка вала длиной 1 м не должен превышать предельной величины, определяемой требованиями конструкции.
Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ0°].
Расчетная формула на жесткость при кручении имеет вид:
φ0° = 180 Мкр / (пGIr) ≤ [φ0°]
В реальных механизмах обычно допускаются углы закручивания валов в пределах [φ0°] = 0,25…1 градус/м.
Пример решения задачи на кручение
Определить минимальный допустимый диаметр вала d, передающего крутящий момент Мкр = 464 Нм, если допускаемое напряжение кручения [τкр] = 30 МПа.
Решение
По известному передаваемому крутящему моменту можно определить момент сопротивления кручению:
Wr = Мкр / [τкр] = 464 / 30 х 106 = 15,6 х 10-6 м3.
Из зависимости между моментом сопротивления кручению и диаметром вала Wr ≈ 0,2D3 находим минимальный допустимый диаметр:
D ≈ 3√(Wr / 0,02) ≈ 43 мм (здесь и далее √ — знак корня).
Округляя найденное значение диаметра до стандартной величины (в большую сторону), принимаем D = 45 мм.
***
Потенциальная энергия деформации при кручении
Представим себе круглый цилиндрический брус (вал) постоянного сечения, жестко защемленный одним концом и нагруженный на другом конце моментом, приложенным статически, т. е. медленно возрастающим от нуля до какого-либо значения Т.
Полагаем, что момент остается в пределах, когда нагрузка и деформация пропорциональны, т. е. справедлив закон Гука.
Момент Т вызывает в брусе деформацию кручения и при этом совершает работу W, которая аккумулируется в виде потенциальной энергии деформации U, причем пренебрегая незначительными потерями энергии (например, на нагрев бруса), можно считать, что W = U.
Работа в случае статического нагружения равна: W = Т φ / 2, где φ — полный угол закручивания бруса.
Так как Т = Мкр, то справедливо равенство:
U = W = Т φ / 2 = Мкр2 l / (2Glr).
При одновременном действии нескольких моментов или ступенчатом изменении размеров поперечного сечения брус разбивают на однородные участки и потенциальную энергию деформации всего бруса определяют как сумму потенциальных энергий этих участков.
***
Материалы раздела «Деформация кручения»:
- Понятие о кручении цилиндрического бруса (вала)
- Построение эпюр крутящих моментов
- Деформации и напряжения, возникающие при кручении
- Расчеты на прочность и жесткость при кручении
- Расчет цилиндрических винтовых пружин
Деформация среза
Источник
| ОСНОВНОЕ УСЛОВИЕ ПРОЧНОСТИ. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. УСЛОВИЕ ЖЕСТКОСТИ |
| Ответы на вопросы о прочности может дать оценка прочности конструкции, которая сводится к сравнению расчетных напряжений с допускаемыми: |
| Это и есть основные условия прочности. |
| Расчетное напряжение — наибольшее по абсолютной величине сжимающее или стягивающее напряжение, возникающее в опасном сечении конструкции. |
| Допускаемые напряжения. |
| Допускаемое напряжение определяется по формуле: |
| Механические характеристики материалов — величины предела текучести и предела прочности определяются опытным путем. Автоматически вычерчивается график «сила — продольная деформация» (Р -l) Этот график переводится в диаграмму напряжение — относительная деформация . |
| где . (Здесь F0 и l0 — первоначальная площадь поперечного сечения и длина стандартного образца) (рис. 1.22). |
| Рис. 1.22 |
| — предел пропорциональности; наибольшее напряжение, при котором еще справедлив закон Гука; |
| — предеп текучести (деформации растут без увеличения нагрузки); |
| Рис. 1.23 |
| — предел прочности ипи временное сопротивпение разрыву (рис.1 23). |
| — предел прочности при растяжении, |
| — предеп прочности при сжатии, причем: |
| В спучае пластичного материапа в качестве предельного напряжения |
| — принимается предеп текучести при растяжении , соответствующий началу текучести материала, а в случае хрупкого материала — предел прочности при растяжении или сжатии, предшествующий разрыву образца. |
| В знаменателе стоит нормативный (требуемый) коэффициент запаса прочности по отношению соответственно к пределу текучести и пределу прочности n. |
| Он представляет собой величину, большую единицы, зависящую от класса конструкции (капитальная, временная и т.п.), срока ее эксплуатации, нагрузки (статическая, циклическая и т.п.), возможной неоднородности изготовления материала и от вида деформации (растяжение, сжатие, изгиб и т.п.). |
| Нормативный коэффициент запаса прочности регламентируется для строительных конструкций СН и Пами, для машиностроительных — внутризаводскими нормами. В большинстве случаев он принимается равным для пластичных материалов nT = 1,5 + 2,5, для хрупких nB = 2,5 + 5. |
| В случае, когда решающими для прочности конструкции являются не нормальные, а касательные напряжения (например, при кручении бруса круглого поперечного сечения), условие прочности имеет вид: |
| — расчетное касательное напряжение. |
| — допускаемое касательное напряжение, определяемое по формуле: |
| В случае пластичного материала в качестве предельного принимают предел текучести при сдвиге в случае хрупкого материала — предел прочности . |
| В большинстве случаев допускаемые напряжения при кручении принимают в зависимости от допускаемых напряжений при растяжении того же материала. Например, для стали = 0,5 [], для чугуна . |
| В практике инженерных расчетов считают возможным допускать перенапряжение материала до 3 — 5%. |
| Условие жесткости по логике строится так же, как и условие прочности. Однако, ограничения накладываются не на напряжения, а на изменение формы стержня (вала, балки), т.е. деформации. Для разных видов нагружения условия жесткости имеютвид: при растяжении (сжатии) |
| при кручении |
| где — угол закручивания, |
| при изгибе |
| где — угол поворота, у — прогиб. |
Источник
