Укажите единицу си абсолютной деформации при растяжении
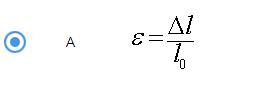

Пределом упругости называют величину, равную наибольшему напряжению, при котором
деформация сохраняет обратимый упругий характер
Пределом прочности называют величину, равную наибольшему напряжению которое способен
выдержать образец без разрушения
По диаграмме растяжения определяют, в частности, значение предела упругости
Диаграммой растяжения называют зависимость механического напряжения от относительной
деформации твердых тел при растяжении
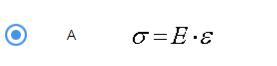
Укажите формулу закона Гука:
Упругой называется деформация, которая после прекращения действия силы полностью
исчезает
Пластической называется деформация, которая не исчезает после снятия нагрузки, она необратимо изменяет начальные размеры образца
При деформации сдвига внешняя сила направлена по касательной к поверхности тела
При деформации растяжения внешняя сила направлена вдоль оси деформируемого тела
Укажите единицу СИ модуля упругости Па или Н/м2
Закон Гука выполняется при любых способах деформирования тел, но только при малых деформациях и небольших значениях напряжения
Относительной деформацией при растяжении называется величина, равная отношению
абсолютного удлинения к первоначальной длине образца
При упругой деформации происходит обратимое изменение формы образца
При упругой деформации между механическим напряжением и относительной деформацией существует зависимость прямо пропорциональная
Укажите единицу СИ абсолютной деформации при растяжении: м
Механическим напряжением называется величина, равная отношению силы, приложенной к
сечению, к площади сечения
Деформацией называется изменение взаимного расположения точек тела, которое приводит к изменению его формы и размеров, под действием внешних факторов
При определении механического напряжения при деформации растяжения и сжатия
учитывается, в частности, площадь сечения образца, на которое действует деформирующая сила
При действии деформирующей силы в образце возникают внутренние силы, мерой
которых является механическое напряжение
При упругой деформации растяжения происходит удлинение образца
Деформацией, которая после прекращения действия силы полностью исчезает, называют деформацией упругой
При деформации изгиба материал, находящийся в нейтральном слое не испытывает
деформации растяжения или сжатия
Укажите формулу для определения относительной деформации при одноосном растяжении:
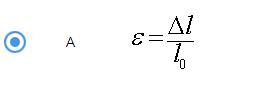
Изгиб — это вид деформации, который характеризуется . . . срединного (нейтрального) слоя деформируемого объекта (балки, стержня) под действием внешних сил искривлением
Модуль упругости численно равен: напряжению, при котором длина образца увеличивается вдвое
ПРАВИЛЬНЫЕ УТВЕРЖДЕНИЯ
Пластичность — свойство материала деформироваться без разрушения под действием внешних сил и сохранять новую форму после прекращения их действия
Единицы СИ модуля упругости и механического напряжения одинаковы (измеряются в Паскалях)
Предел упругости — напряжение, ниже которого деформация сохраняет упругий обратимый характер
Сдвиг — вид деформации, возникающей в случае, когда на тело действует касательная сила, приложенная параллельно закрепленному основанию
Закон Гука выполняется только при малых деформациях и небольших значениях напряжения
Относительная деформация при растяжении (сжатии) — величина, равная отношению абсолютного удлинения к первоначальной длине образца
При упругой деформации растяжения (сжатия) происходит обратимое изменение формы образца
Относительная деформация — безразмерная величина
Пластическая деформация — это деформация, которая не исчезает после снятия нагрузки, она необратимо изменяет начальные размеры образца
Модуль Юнга численно равен механическому напряжению, при котором длина образца увеличивается вдвое Деформация при изгибе характеризуется стрелой прогиба Относительная деформация — безразмерная величина
При упругой деформации растяжения (сжатия) происходит обратимое изменение формы образца
НЕПРАВИЛЬНЫЕ УТВЕРЖДЕНИЯ
Упругая деформация проявляется в любых материалах при длительном действии постоянной нагрузки При деформации изгиба материал, находящийся в нейтральном слое подвергается деформации растяжения или сжатия Предел прочности — деформация, начиная с которой в образце развивается текучесть
Растяжение (сжатие) — вид деформации, возникающей в случае, когда к стержню (бруску) с закрепленным основанием прикладывается сила F, направленная поперек его оси
Относительная деформация при растяжении (сжатии) — величина, равная отношению конечной длины образца к его абсолютному удлинению

Закон Гука выполняется при любых деформациях и любых значениях напряжения Единицей СИ относительной деформации является м
Модуль упругости при растяжении — напряжение, при котором длина образца уменьшается вдвое При длительном действии постоянной нагрузки во всех материалах проявляется вязкоупругая деформация Пластическая деформация — это деформация, которая частично исчезает после снятия напряжения
Модуль Юнга численно равен механическому напряжению, при котором длина образца увеличивается на 50%
Модуль упругости при растяжении — напряжение, при котором длина образца уменьшается вдвое Предел текучести — это относительная деформации, начиная с которой деформация становится текучей
Источник
    Äëÿ îòäåëüíî âçÿòîãî ýëåìåíòà êîíñòðóêöèè âçàèìîóðàâíîâåøåííûå àêòèâíàÿ ñèëà è ñèëà ðåàêöèè îïîðû ÿâëÿþòñÿ
âíåøíèìè ñèëàìè.
    Ðàññìîòðèì, êàêèì îáðàçîì êîíñòðóêöèÿ îêàçûâàåò ñîïðîòèâëåíèå âíåøíåé íàãðóçêå, çà ñ÷åò ÷åãî ïðîèñõîäèò èçìåíåíèå
ôîðìû è ðàçìåðîâ êîíñòðóêöèè — äåôîðìèðîâàíèå (îò ëàò. deformatio — èñêàæåíèå).
10.3.1. Ðàñòÿæåíèå
    Íå îáðàùàÿ âíèìàíèå íà òî, êàêèì îáðàçîì, ñ òî÷êè çðåíèÿ êîíñòðóêòèâíîãî ðåøåíèÿ, ïðèëîæåíû âíåøíèå ñèëû Ð,
ðàññìîòðèì ðàñòÿæåíèå ýëåìåíòà êîíñòðóêöèè, ñõåìà íàãðóæåíèÿ êîòîðîãî ïîêàçàíà íà ðèñ. 10.3,à.
|
Ðèñ. 10.3. Óïðîùåííàÿ ìîäåëü äåôîðìàöèè ïðè ðàñòÿæåíèè |
Íà ðèñ. 10.3 ïîêàçàíà òàêæå óïðîùåííàÿ ìîäåëü ìåæàòîìíûõ ñâÿçåé â òâåðäîì òåëå. Æåñòêèå è ïðî÷íûå ìåæàòîìíûå ñâÿçè, ñîåäèíÿþùèå àòîìû
íåäåôîðìèðîâàííîãî òåëà (ðèñ. 10.3,á), ïðè ðàñòÿæåíèè (ðèñ. 10.3,â) ñîçäàþò áîëüøèå
âíóòðåííèå ñèëû ïðîòèâîäåéñòâèÿ âíåøíåé íàãðóçêå, ñòðåìÿùèåñÿ ñîõðàíèòü òåëî êàê åäèíîå öåëîå.
    Ïîä äåéñòâèåì âíåøíèõ ñèë ÷àñòèöû (àòîìû) ìàòåðèàëà, èç êîòîðîãî ñäåëàíà êîíñòðóêöèÿ, áóäóò ïåðåìåùàòüñÿ, è
ïåðåìåùåíèå ÷àñòèö ïîä íàãðóçêîé áóäåò ïðîäîëæàòüñÿ, ïîêà ìåæäó âíåøíèìè è âíóòðåííèìè ñèëàìè íå óñòàíîâèòñÿ ðàâíîâåñèå.
    Òàêîå ñîñòîÿíèå íàçûâàåòñÿ äåôîðìèðîâàííûì
ñîñòîÿíèåì òåëà.
    Ìåðîé âîçäåéñòâèÿ âíåøíèõ ñèë íà àòîìû âåùåñòâà, êîòîðûå óäàëÿþòñÿ äðóã îò äðóãà (ïðè ðàñòÿæåíèè) èëè ñáëèæàþòñÿ
(ïðè ñæàòèè), ò. å. ìåðîé ïðîòèâîäåéñòâèÿ ìàòåðèàëà êîíñòðóêöèè âíåøíåìó ñèëîâîìó âîçäåéñòâèþ, ìåðîé âíóòðåííèõ ñèë â ìàòåðèàëå ÿâëÿåòñÿ
íàïðÿæåíèå. Íàïðÿæåíèåì íàçûâàåòñÿ âíóòðåííÿÿ ñèëà (âîçíèêàþùàÿ ïðè âîçäåéñòâèè âíåøíåé íàãðóçêè),
ïðèõîäÿùàÿñÿ íà åäèíèöó ïëîùàäè â îêðåñòíîñòè äàííîé òî÷êè ðàññìàòðèâàåìîãî ñå÷åíèÿ òåëà:
σ = Ð/F,
| ãäå    | σ |    - | íàïðÿæåíèå, Ïà (1Ïà=1Í/ì2); |
| P |    - | ñóììàðíàÿ ñèëà, Í; | |
| F |    - | ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ, ïåðïåíäèêóëÿðíîãî íàïðàâëåíèþ äåéñòâóþùåé ñèëû P,ì2. |
   Â èíæåíåðíîé ïðàêòèêå èíîãäà èçìåðÿþò íàïðÿæåíèÿ â äàÍ/ìì2 (1äàÍ= 10Í).
   Íàïðÿæåíèå, òàêèì îáðàçîì, ïîêàçûâàåò èíòåíñèâíîñòü ïðîòèâîäåéñòâèÿ âíóòðåííèõ ñèë âîçäåéñòâèþ âíåøíåé íàãðóçêè íà
ìåæàòîìíûå ñâÿçè ìàòåðèàëà êîíñòðóêöèè, èëè, ÷òî òî æå ñàìîå, èíòåíñèâíîñòü âîçäåéñòâèÿ âíåøíåé íàãðóçêè íà ìåæàòîìíûå ñâÿçè.
   Åñëè ðàññìîòðåòü äåôîðìèðîâàííîå ñîñòîÿíèå ñòåðæíÿ (áðóñà) (ðèñ. 10.4) ïðè ðàñòÿæåíèè âíåøíèìè ñèëàìè Ð
(ïîêàçàíû íà ðèñóíêå ÷åðíûìè ñòðåëêàìè), òî â ëþáîì ïðîèçâîëüíî âçÿòîì ïîïåðå÷íîì ñå÷åíèè (íàïðèìåð, ïëîñêîñòüþ À) ðàñïðåäåëåíèå
íîðìàëüíûõ íàïðÿæåíèé σ = Ð/F áóäåò ðàâíîìåðíûì.
|
Ðèñ. 10.4. Äåôîðìèðîâàííîå ñîñòîÿíèå áðóñà |
   Ðàâíîäåéñòâóþùàÿ ñèëà íàïðÿæåíèé σ — âíóòðåííÿÿ ñèëà
Ð = σF (íà ðèñ. 10.4 — áåëàÿ ñòðåëêà) — ïðîõîäèò ÷åðåç öåíòð òÿæåñòè ïîïåðå÷íîãî ñå÷åíèÿ âäîëü ëèíèè äåéñòâèÿ
âíåøíåé ñèëû è ðàâíà åé.
   Ïîä äåéñòâèåì ðàñòÿãèâàþùèõ ñèë Ð äëèíà ñòåðæíÿ l óâåëè÷èâàåòñÿ íà âåëè÷èíó Δl,
íàçûâàåìóþ àáñîëþòíûì óäëèíåíèåì. Ðàñòÿæåíèå ñîïðîâîæäàåòñÿ òàêæå óìåíüøåíèåì ïîïåðå÷íûõ ðàçìåðîâ
ñå÷åíèÿ. Ýòî ÿâëåíèå íîñèò íàçâàíèå «ýôôåêò Ïóàññîíà» (ïî èìåíè ôðàíöóçñêîãî ó÷åíîãî è ìåõàíèêà
Ñ. Ïóàññîíà). Àáñîëþòíîå ïîïåðå÷íîå ñóæåíèå
ñòåðæíÿ ïðè ðàñòÿæåíèè Δb =
b — b1; Δc = c — c1.
   Èìåííî çà ñ÷åò èçìåíåíèÿ ôîðìû è ðàçìåðîâ ëþáàÿ êîíñòðóêöèÿ ñîïðîòèâëÿåòñÿ (ñîçäàåò ñèëû ïðîòèâîäåéñòâèÿ) âíåøíèì íàãðóçêàì.
   Â èíæåíåðíîé ïðàêòèêå äåôîðìèðîâàííîå ñîñòîÿíèå ïðèíÿòî îöåíèâàòü íå òîëüêî àáñîëþòíûìè âåëè÷èíàìè èçìåíåíèé ôîðìû
( «ïåðåìåùåíèÿìè»), íî è îòíîñèòåëüíûìè áåçðàçìåðíûìè âåëè÷èíàìè —
«äåôîðìàöèÿìè»:
ε = Δl/l; ε = Δb/b = Δc/c,
| ãäå    | ε |    - | îòíîñèòåëüíîå óäëèíåíèå ïðè ðàñòÿæåíèè; |
| ε’ |    - | îòíîñèòåëüíûå ïîïåðå÷íûå äåôîðìàöèè. |
   Ïðè äîñòàòî÷íî áîëüøèõ âíåøíèõ íàãðóçêàõ (è, êàê ñëåäñòâèå, áîëüøèõ âíóòðåííèõ íàïðÿæåíèÿõ) ìåæàòîìíûå ñâÿçè ìàòåðèàëà ìîãóò
áûòü ðàçîðâàíû, ÷òî ïðèâåäåò ê ðàçðóøåíèþ êîíñòðóêöèè.
   Êîíñòðóêöèÿ äîëæíà áûòü ñïðîåêòèðîâàíà òàê, ÷òîáû îíà íå ðàçðóøèëàñü ïîä íàãðóçêîé. Äåôîðìàöèè (ïåðåìåùåíèÿ), êîòîðûå
íåèçáåæíî âîçíèêàþò â êîíñòðóêöèè ïîä íàãðóçêîé, äîëæíû áûòü âïîëíå îïðåäåëåííûìè è äîñòàòî÷íî ìàëûìè, ïîñêîëüêó âûáðàííûå ðàçìåðû è ôîðìà
ýëåìåíòîâ êîíñòðóêöèè îáåñïå÷èâàþò îïðåäåëåííîå êà÷åñòâî åå ôóíêöèîíèðîâàíèÿ.
   Òàê, èçìåíåíèå ïîä íàãðóçêîé ðàçìåðîâ è ôîðìû ýëåìåíòîâ êîíñòðóêöèè ñàìîëåòà, îáòåêàåìûõ ïîòîêîì âîçäóõà, ñóùåñòâåííûì îáðàçîì
âëèÿåò íà àýðîäèíàìè÷åñêèå õàðàêòåðèñòèêè è, êàê ñëåäñòâèå, — íà ëåòíî-òåõíè÷åñêèå õàðàêòåðèñòèêè ñàìîëåòà.
   Õàðàêòåð ðàáîòû êîíñòðóêöèè ïîä íàãðóçêîé âî ìíîãîì îïðåäåëÿåòñÿ âûáîðîì êîíñòðóêöèîííûõ
ìàòåðèàëîâ. Îäíîé èç îñíîâíûõ õàðàêòåðèñòèê ìàòåðèàëà êîíñòðóêöèè ÿâëÿåòñÿ äèàãðàììà ðàñòÿæåíèÿ (êðèâàÿ äåôîðìèðîâàíèÿ) — âçàèìîçàâèñèìîñòü íàïðÿæåíèé è äåôîðìàöèé
óäëèíåíèÿ, ïîëó÷àåìàÿ â ðåçóëüòàòå èñïûòàíèé îáðàçöîâ ìàòåðèàëîâ íà ðàñòÿæåíèå. Íà ðèñ. 10.5 ïîêàçàí òèïè÷íûé õàðàêòåð äèàãðàìì ðàñòÿæåíèÿ äëÿ
íåêîòîðûõ êîíñòðóêöèîííûõ ìàòåðèàëîâ, ïðèìåíÿåìûõ â ñàìîëåòîñòðîåíèè.
|
Ðèñ. 10.5. Äèàãðàììà ðàñòÿæåíèÿ |
   Ïðÿìîëèíåéíûå íà íåêîòîðîì ïðîòÿæåíèè äèàãðàììû ó÷àñòêè (0-À, 0-ÀÂ) õàðàêòåðèçóþò òàêóþ ñòàäèþ äåôîðìèðîâàíèÿ îáðàçöà,
êîãäà ïðè óâåëè÷åíèè íàãðóçêè äåôîðìàöèè ïðîïîðöèîíàëüíû íàïðÿæåíèÿì è ïðè ñíÿòèè íàãðóçêè èñ÷åçàþò, ò. å. îáðàçåö çà ñ÷åò ìåæàòîìíûõ ñâÿçåé
(ñèë óïðóãîñòè) âîçâðàùàåòñÿ â èñõîäíîå (íåäåôîðìèðîâàííîå) ñîñòîÿíèå. Íà ýòîì ó÷àñòêå ìàòåðèàë «ïîä÷èíÿåòñÿ»
çàêîíó Ãóêà (ïî èìåíè àíãëèéñêîãî åñòåñòâîèñïûòàòåëÿ
Ð. Ãóêà):
σ = Åε,
| ãäå    | σ |    - | íàïðÿæåíèå, Ïà; |
| E |    - | ìîäóëü óïðóãîñòè ìàòåðèàëà, èëè ìîäóëü Þíãà (ïî èìåíè àíãëèéñêîãî ó÷åíîãî Ò.Þíãà), Ïà; | |
| ε |    - | îòíîñèòåëüíîå óäëèíåíèå. |
   Ìîäóëü óïðóãîñòè Å (íàêëîí êðèâîé äåôîðìèðîâàíèÿ â çîíå óïðóãîñòè
0-À (0-ÀÂ) äèàãðàììû: Å = tgα) ÿâëÿåòñÿ ìåðîé óïðóãîñòè («æåñòêîñòè») è õàðàêòåðèçóåò ïîäàòëèâîñòü (ñïîñîáíîñòü ê
äåôîðìèðîâàíèþ) ïîä íàãðóçêîé. Îòìåòèì, ÷òî ñòàëü — áîëåå æåñòêèé, ìåíåå ïîäàòëèâûé ìàòåðèàë, ÷åì àëþìèíèåâûé ñïëàâ.
   Òî÷êà À (ÀÂ) íà äèàãðàììàõ õàðàêòåðèçóåò íàèáîëüøóþ íàãðóçêó Ðïö è, ñîîòâåòñòâåííî,
íàïðÿæåíèÿ
ïðåäåëà ïðîïîðöèîíàëüíîñòè
σïö, ïðè êîòîðûõ åùå ñîáëþäàåòñÿ ëèíåéíàÿ
çàâèñèìîñòü σ — ε.
   Äàëüøå, çà òî÷êîé À (ÀÂ), ëèíåéíàÿ çàâèñèìîñòü σ — ε íàðóøàåòñÿ, ìàòåðèàë äåôîðìèðóåòñÿ («òå÷åò»)
ïîä íàãðóçêîé è ïðè ñíÿòèè íàãðóçêè íå âîçâðàùàåòñÿ ê èñõîäíîìó ñîñòîÿíèþ, â íåì âîçíèêàþò îñòàòî÷íûå ïëàñòè÷åñêèå
äåôîðìàöèè çà ñ÷åò òîãî, ÷òî ÷àñòü ìåæàòîìíûõ ñâÿçåé ðàçðóøàåòñÿ. Òî÷êà  íà äèàãðàììàõ õàðàêòåðèçóåò íàãðóçêó
Ðò è, ñîîòâåòñòâåííî,
íàïðÿæåíèÿ ïðåäåëà òåêó÷åñòè
σò, ïðè êîòîðûõ ìàòåðèàë «òå÷åò» áåç óâåëè÷åíèÿ íàãðóçêè. Íåêîòîðûå ìàòåðèàëû (íàïðèìåð, 4, ñì. ðèñ. 10.5)
èìåþò ÿâíî âûðàæåííóþ ïëîùàäêó òåêó÷åñòè À-Â, ãäå äåôîðìàöèè ñóùåñòâåííî óâåëè÷èâàþòñÿ áåç óâåëè÷åíèÿ
âíåøíåé íàãðóçêè. Äëÿ äðóãèõ ìàòåðèàëîâ (1, 2, 3) ïëîùàäêè òåêó÷åñòè îòñóòñòâóþò, â ýòîì ñëó÷àå òî÷êè À è  íà äèàãðàììå ïðàêòè÷åñêè
ñîâïàäàþò.
   Çîíà Â-Ñ äèàãðàììû íàçûâàåòñÿ çîíîé óïðî÷íåíèÿ. Çäåñü ïîñëå ñòàäèè òåêó÷åñòè
ìàòåðèàë ñíîâà ïðèîáðåòàåò ñïîñîáíîñòü óâåëè÷èâàòü ñîïðîòèâëåíèå äàëüíåéøåé äåôîðìàöèè, îäíàêî äëÿ óäëèíåíèÿ îáðàçöà â ýòîé çîíå òðåáóåòñÿ â
ñîòíè ðàç áîëåå ìåäëåííîå íàðàñòàíèå íàãðóçêè, ÷åì â çîíå óïðóãèõ äåôîðìàöèé.
|
Ðèñ. 10.6. Äèàãðàììà èñòèííûõ íàïðÿæåíèé |
   Òî÷êà Ñ äèàãðàììû õàðàêòåðèçóåò ìàêñèìàëüíóþ (ïðåäåëüíóþ) íàãðóçêó Ðmax è, ñîîòâåòñòâåííî,
íàïðÿæåíèÿ ïðåäåëà ïðî÷íîñòè èëè íàïðÿæåíèÿ âðåìåííîãî ñîïðîòèâëåíèÿ σâ, ïðè êîòîðûõ åùå ñîõðàíÿåòñÿ öåëîñòíîñòü
ýëåìåíòà êîíñòðóêöèè, íàãðóæåííîãî ðàñòÿæåíèåì.
   Äàëüøå, çà òî÷êîé Ñ äèàãðàììû, áåç óâåëè÷åíèÿ âíåøíåé íàãðóçêè èäåò ëàâèíîîáðàçíîå ðàçðóøåíèå ìåæàòîìíûõ ñâÿçåé
ìàòåðèàëà.
   Íàïðÿæåíèå σâ, òàêèì îáðàçîì, õàðàêòåðèçóåò ïðî÷íîñòü ìàòåðèàëà íà ðàçðûâ.
   Òî÷êà D äèàãðàììû õàðàêòåðèçóåò ðàçðóøåíèå (ðàçðûâ) îáðàçöà. Íèñõîäÿùàÿ âåòâü äèàãðàììû Ñ-D èìååò óñëîâíûé
õàðàêòåð, ïîñêîëüêó íàïðÿæåíèÿ ðàññ÷èòûâàþòñÿ äëÿ ïëîùàäè ïîïåðå÷íîãî ñå÷åíèÿ èñõîäíîãî îáðàçöà. Ðåàëüíî íàïðÿæåíèÿ ðàñòóò, ÷òî ïîêàçûâàåò
äèàãðàììà èñòèííûõ íàïðÿæåíèé (ðèñ. 10.6 — ïóíêòèðíàÿ ëèíèÿ),
â êîòîðîé íàïðÿæåíèÿ ðàññ÷èòûâàþòñÿ äëÿ èñòèííîé ïëîùàäè ïîïåðå÷íîãî ñå÷åíèÿ îáðàçöà.  èíòåðâàëå Î-À ðîñò íàïðÿæåíèÿ èäåò áåç
ðàçðóøåíèÿ ìåæàòîìíûõ ñâÿçåé, ïîñëå ñíÿòèÿ íàãðóçêè îáðàçåö âîçâðàùàåòñÿ ê èñõîäíîìó ñîñòîÿíèþ. Â èíòåðâàëå À-D ðîñò íàïðÿæåíèÿ
ïðîèñõîäèò çà ñ÷åò ðàçðóøåíèÿ ìåæàòîìíûõ ñâÿçåé è çíà÷èòåëüíîãî ìåñòíîãî óòîíåíèÿ îáðàçöà (îáðàçîâàíèÿ
øåéêè 1).  ìîìåíò ðàçðóøåíèÿ (òî÷êà D äèàãðàììû) ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ïëàñòè÷åñêè
äåôîðìèðîâàííîãî îáðàçöà ìåíüøå èñõîäíîé.
   Ïðî÷íîñòü êîíñòðóêöèè, åñòåñòâåííî, çàâèñèò îò ïðî÷íîñòè ìàòåðèàëà, èç êîòîðîãî îíà èçãîòîâëåíà.
   Ïðî÷íîñòü
(íåñóùàÿ ñïîñîáíîñòü)
êîíñòðóêöèè — ýòî ñïîñîáíîñòü êîíñòðóêöèè â îïðåäåëåííûõ óñëîâèÿõ âîñïðèíèìàòü (âûäåðæèâàòü) áåç
ðàçðóøåíèÿ âíåøíèå íàãðóçêè.
Íàãðóçêà, ïðè êîòîðîé ïðîèñõîäèò ðàçðóøåíèå êîíñòðóêöèè, íàçûâàåòñÿ
ðàçðóøàþùåé.
|
Ðèñ. 10.7. Òðàåêòîðèè íàïðÿæåíèé |
   Íåñóùàÿ ñïîñîáíîñòü âî ìíîãîì çàâèñèò îò ïëàñòè÷íîñòè ìàòåðèàëà. Ïëàñòè÷íîñòü
— ñïîñîáíîñòü ìàòåðèàëà ïîëó÷àòü áîëüøèå îñòàòî÷íûå äåôîðìàöèè, íå ðàçðóøàÿñü. Õðóïêîñòü
(ñâîéñòâî, ïðîòèâîïîëîæíîå ïëàñòè÷íîñòè) — ñïîñîáíîñòü ìàòåðèàëà ðàçðóøàòüñÿ áåç çàìåòíîé ïëàñòè÷åñêîé äåôîðìàöèè.
   Æåñòêîñòü — ñïîñîáíîñòü êîíñòðóêöèè ñîïðîòèâëÿòüñÿ äåéñòâèþ âíåøíèõ íàãðóçîê
ñ äîïóñòèìûìè â ýêñïëóàòàöèè äåôîðìàöèÿìè, íå íàðóøàþùèìè ðàáîòîñïîñîáíîñòü êîíñòðóêöèè.
   Íåñóùàÿ ñïîñîáíîñòü êîíñòðóêöèè ðåçêî ñíèæàåòñÿ èìåþùèìèñÿ â ìàòåðèàëå êîíñòðóêöèè ìèêðîòðåùèíàìè, âêðàïëåíèÿìè
èíîðîäíûõ ìàòåðèàëîâ, íàðóøàþùèìè ïîñòîÿíñòâî íàïðÿæåíèé.
   Êîíöåíòðàòîðû íàïðÿæåíèé
— ìåñòíûå ðåçêèå èçìåíåíèÿ îäíîðîäíîñòè (ôîðìû è, ñëåäîâàòåëüíî, æåñòêîñòè) êîíñòðóêöèè, ïðèâîäÿùèå ê ðåçêîìó ìåñòíîìó
(ëîêàëüíîìó) ïîâûøåíèþ íàïðÿæåíèé â êîíñòðóêöèè.
   Íà ðèñ. 10.7 ïîêàçàíî äåéñòâèå ðàñòÿãèâàþùåé âíåøíåé íàãðóçêè, ðàâíîìåðíî ðàñïðåäåëåííîé ïî êðàÿì ïðîñòåéøèõ êîíñòðóêòèâíûõ
ýëåìåíòîâ — ëèñòîâ. Ïóíêòèðíûå ëèíèè ïðåäñòàâëÿþò ñîáîé òàê íàçûâàåìûå òðàåêòîðèè íàïðÿæåíèé, âäîëü êîòîðûõ íàïðÿæåíèå ïåðåäàåòñÿ îò
ìîëåêóëû ê ìîëåêóëå. Äëÿ ãëàäêîãî ëèñòà ýòè ëèíèè ïàðàëëåëüíû, íàïðÿæåíèÿ â ëþáîì ñå÷åíèè ëèñòà îäèíàêîâû.
|
Ðèñ. 10.8. ïåðåäà÷à íàãðóçêè â ñîåäèíåíèè |
   Ñèëû, ïåðåäàþùèåñÿ ïî òðàåêòîðèÿì íàïðÿæåíèé â ëèñòàõ ñ êîíöåíòðàòîðàìè (íàäðåç â êðîìêå ëèñòà, îòâåðñòèå â öåíòðå ëèñòà),
îáõîäÿò ðàçðûâ â ìàòåðèàëå. Ïëîòíîñòü òðàåêòîðèé íàïðÿæåíèé óâåëè÷èâàåòñÿ, è ëîêàëüíûå íàïðÿæåíèÿ σ ó êðàÿ êîíöåíòðàòîðà âîçðàñòàþò
(èíîãäà ìíîãîêðàòíî). Â ýòèõ ìåñòàõ ìîæåò ïðîèçîéòè íàðóøåíèå (ðàçðûâ) ìåæàòîìíûõ ñâÿçåé, âîçíèêíóò ìèêðîòðåùèíû, ðàñïðîñòðàíåíèå êîòîðûõ âåäåò
ê ðàçðóøåíèþ êîíñòðóêöèè.
   Ðàñïðåäåëåíèå íàïðÿæåíèé â çàêîíöîâêàõ (ìåñòàõ ñîåäèíåíèÿ äåòàëåé)
îáû÷íî îñîáåííî
ñëîæíî, â íèõ îáÿçàòåëüíî ïîÿâëÿþòñÿ êîíöåíòðàöèè íàïðÿæåíèé
— ìåñòíîå ïîâûøåíèå íàïðÿæåíèé.
   Â ìåñòå ñîåäèíåíèÿ (ðèñ. 10.8) ëèñòîâ 1 è 3 ñ ïîìîùüþ çàêëåïîê (èëè ñâàðíûõ òî÷åê) 2 ïåðåäà÷à
íàãðóçêè áóäåò
ïðîèñõîäèòü òîëüêî ÷åðåç òî÷êè êðåïëåíèÿ. Ëèñòû ðàâíîìåðíî âêëþ÷àòñÿ â ðàáîòó íà äîñòàòî÷íî áîëüøîì óäàëåíèè îò ìåñòà
ñîåäèíåíèÿ.
   Çàøòðèõîâàííàÿ îáëàñòü ëèñòîâ ïðàêòè÷åñêè âûêëþ÷åíà èç ðàáîòû è íå èñïûòûâàåò íàïðÿæåíèé.  òî æå âðåìÿ
íàïðÿæåíèÿ â ïîïåðå÷íûõ ñå÷åíèÿõ ëèñòîâ ðàñïðåäåëåíû íåðàâíîìåðíî, ïðè÷åì σÀ-À > σÁ-Á > σÂ-Â.
   Êîíñòðóêòîð îñîáîå âíèìàíèå äîëæåí óäåëÿòü âûáîðó ôîðìû äåòàëåé, ðàáîòàþùèõ íà ðàñòÿæåíèå, è îñîáåííî èõ
çàêîíöîâîê, ÷òîáû óìåíüøèòü âîçìîæíûå êîíöåíòðàöèè íàïðÿæåíèé.
Источник
26.На приведенной ниже типичной диаграмме растяжения укажите участок кривой,
соответствующий текучести материала CD
27.Укажите график закона Гука:
28.На приведенной ниже типичной диаграмме растяжения укажите участок кривой, соответствующий упругой деформации
0B
Укажите правильные высказывания:
Закон Гука выполняется при любых деформациях и любых значениях напряжения
A
| + | Закон Гука выполняется только при малых деформациях и небольших значениях | |
| напряжения | ||
| B |
Относительная деформация при растяжении (сжатии) — величина,
C равная отношению конечной длины образца к его абсолютному удлинению
Относительная деформация при растяжении (сжатии) — величина, равная отношению абсолютного удлинения к первоначальной длине образца
Укажите правильные высказывания:
| + | Единицы СИ модуля упругости и механического напряжения одинаковы | |||
| A | ||||
| + | При деформации изгиба материал, находящийся в нейтральном слое | |||
| подвергается деформации растяжения или сжатия | ||||
| D | B | |||
Пластичность — свойство материала деформироваться без разрушения под
+ действием внешних сил и сохранять новую форму после прекращения их
C действия
Упругая деформация проявляется в любых материалах при длительном
D действии постоянной нагрузки
Укажите правильные высказывания:
| + | Деформация при изгибе характеризуется стрелой прогиба | ||
| A | |||
| Предел текучести — это относительная деформации, начиная с которой | |||
| B | деформация становится текучей | ||
| Модуль Юнга численно равен механическому напряжению, при котором длина | |||
| C | образца увеличивается на 50% | ||
| + | Модуль Юнга численно равен механическому напряжению, при котором длина | ||
| образца увеличивается вдвое | |||
| D | |||
Укажите правильные высказывания:
| Модуль упругости при растяжении — напряжение, при котором длина образца | |||
| A | уменьшается вдвое | ||
| + | При упругой деформации растяжения (сжатия) происходит обратимое | ||
| изменение формы образца | |||
| B | |||
| + | Относительная деформация — безразмерная величина | ||
| C | |||
| Единицей СИ относительной деформации является м | |||
| D |
Укажите правильные высказывания:
Пластическая деформация — это деформация, которая не исчезает после снятия
+ A нагрузки, она необратимо изменяет начальные размеры образца
При длительном действии постоянной нагрузки во всех материалах проявляется B вязкоупругая деформация
Пластичность — свойство материала деформироваться без разрушения под
+ действием внешних сил и сохранять новую форму после прекращения их действия
C
Пластическая деформация — это деформация, которая частично исчезает после D снятия напряжения
Укажите правильные высказывания:
Растяжение (сжатие) — вид деформации, возникающей в случае, когда к стержню (бруску) с закрепленным основанием прикладывается сила F, направленная
A поперек его оси
Предел прочности — деформация, начиная с которой в образце развивается B текучесть
| + | Предел упругости — напряжение, ниже которого деформация сохраняет упругий | ||
| обратимый характер | |||
| C | |||
| + | Сдвиг — вид деформации, возникающей в случае, когда на тело действует | ||
| касательная сила, приложенная параллельно закрепленному основанию | |||
| D | |||
Установите соответствия:
A
B
Величина, равная отношению абсолютного удлинения к первоначальной длине образца
Величина, равная отношению силы, приложенной к сечению, к площади сечения
Относительное удлинение
Механическое напряжение
| Величина, равная изменению длины | |||||
| C | образца | Абсолютное удлинение | |||
Установите соответствия видов деформации и их характеристик:
| Относительное удлинение | |||||
| A | Растяжение (сжатие) | ||||
Угол сдвига
B
Стрела прогиба
C
Установите соответствия:
A
B
C
Установите соответствия:
Сдвиг
Изгиб
Абсолютное удлинение
Механическое напряжение
Относительное удлинение
A
B
C
Увеличение относительного удлинения образца при постоянном механическом напряжении
Полностью исчезает после прекращения действия силы
Не исчезает после снятия нагрузки, она необратимо изменяет начальные размеры образца
Текучесть
Упругая деформация
Пластическая деформация
В приведенной формуле закона Гука
Относительное удлинение
A
Механическое напряжение
B
ε
σ
Модуль упругости
C
Установите соответствия:
E
A
B
C
Напряжение, при котором происходит рост деформации без заметного увеличения нагрузки
Наибольшее напряжение, при котором деформация сохраняет обратимый упругий характер
Наибольшее напряжение, которое способен выдержать образец без разрушения
Предел текучести
Предел упругости
Предел прочности
Установите соответствияединиц измерения и характеристик механической деформации:
| Н | ||||||
| A | Действующая сила | |||||
| м | |||||||
| B | Абсолютное удлинение | ||||||
| безразмерная величина | |||||||
| C | Относительное удлинение | ||||||
| Н/м2 | |||||||
| D | Механическое напряжение | ||||||
Течение и вязкость жидкости
Выберите правильный ответ
1.При стационарном (ламинарном) движении слоев жидкости с различными скоростями между ними возникают касательные силы трения, . . . площади их соприкосновения пропорциональные
2.Укажите график зависимости коэффициента вязкости плазмы крови от градиента
скорости 3.Укажите график зависимости коэффициента вязкости цельной крови от градиента
скорости
4.Гидравлическое сопротивление сосуда (трубы) . . . динамической вязкости жидкости прямо пропорционально
5.Укажите формулу, по которой определяют число Рейнольдса
6.Силы внутреннего трения, возникающие при относительном движении смежных слоев жидкости, направлены . . . касательно к поверхности слоев
7.При турбулентном течении жидкости число Рейнольдса . . . больше критического
8.При ламинарном течении жидкости число Рейнольдса . . . меньше критического
9.При охлаждении жидкости ее вязкость . . . увеличивается
10.На шарик, движущийся в вязкой жидкости, действует сила сопротивления, которая определяется законом Стокса:
11.Гидравлическое сопротивление сосуда (трубы) определяют по формуле:
12.Укажите единицу СИ динамической вязкости: Па . с
13. Объем жидкости Q, протекающей через горизонтальную трубу радиуса R за 1 с определяется формулой Пуазейля, имеющей вид:
14.При нагревании жидкости ее вязкость . . . уменьшается
15.Укажите единицу СИ кинематической вязкости: м2/с
16.При ламинарном течении ньютоновских жидкостей по цилиндрическим сосудам с удалением от центра сосуда скорость движения слоев жидкости . . . уменьшается
17.При определении вязкости методом Стокса движение шарика в жидкости должно быть . . . равномерным
18.Силы внутреннего трения, возникающие при относительном движении смежных слоев жидкости, пропорциональны . . . площади поверхности соприкасающихся слоев
19.Уравнение Ньютона для вязкой жидкости имеет вид:
20.Кровь является неньютоновской жидкостью, так как . . . она содержит склонные к
Источник






