Удельная работа деформации при растяжении

Лабораторная работа № 1
Цель работы – изучить поведение малоуглеродистой стали при растяжении и определить ее механические характеристики.
Основные сведения
Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.
Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.
В таких случаях, кроме металлографических исследований, определяются главные механические характеристики на образцах, взятых из зоны разрушения конструкции. Образцы изготавливаются по ГОСТ 1497-84 и могут иметь различные размеры и форму (рис. 1.1).
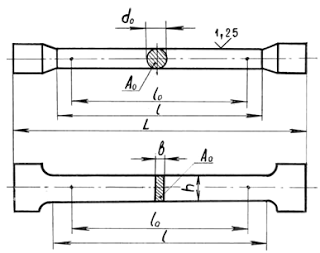
Рис. 1.1. Образцы для испытания на растяжение
Между расчетной длиной образца lо и размерами поперечного сечения Ао (или dо для круглых образцов) выдерживается определенное соотношение:
В испытательных машинах усилие создается либо вручную — механическим приводом, либо гидравлическим приводом, что присуще машинам с большей мощностью.
В данной работе используется универсальная испытательная машина УММ-20 с гидравлическим приводом и максимальным усилием 200 кН, либо учебная универсальная испытательная машина МИ-40КУ (усилие до 40 кН).
Порядок выполнения и обработка результатов
Образец, устанавливаемый в захватах машины, после включения насоса, создающего давление в рабочем цилиндре, будет испытывать деформацию растяжения. В измерительном блоке машины есть шкала с рабочей стрелкой, по которой мы наблюдаем рост передаваемого усилия F.
Зависимость удлинения рабочей части образца от действия растягивающей силы во время испытания отображается на миллиметровке диаграммного аппарата в осях F-Δl (рис. 1.2).
В начале нагружения деформации линейно зависят от сил, потому участок I диаграммы называют участком пропорциональности. После точки В начинается так называемый участок текучести II.
На этой стадии стрелка силоизмерителя как бы спотыкается, приостанавливается, от точки В на диаграмме вычерчивается либо прямая, параллельная горизонтальной оси, либо слегка извилистая линия — деформации растут без увеличения нагрузки. Происходит перестройка структуры материала, устраняются нерегулярности в атомных решетках.
Далее самописец рисует участок самоупрочнения III. При дальнейшем увеличении нагрузки в образце происходят необратимые, большие деформации, в основном концентрирующиеся в зоне с макронарушениями в структуре – там образуется местное сужение — «шейка».
На участке IV фиксируется максимальная нагрузка, затем идет снижение усилия, ибо в зоне «шейки» сечение резко уменьшается, образец разрывается.
При нагружении на участке I в образце возникают только упругие деформации, при дальнейшем нагружении появляются и пластические — остаточные деформации.
Если в стадии самоупрочнения начать разгружать образец (например, от т. С), то самописец будет вычерчивать прямую СО1. На диаграмме фиксируются как упругие деформации Δlу (О1О2), так и остаточные Δlост (ОО1). Теперь образец будет обладать иными характеристиками.
Так, при новом нагружении этого образца будет вычерчиваться диаграмма О1CDЕ, и практически это будет уже другой материал. Эту операцию, называемую наклеп, широко используют, например, в арматурных цехах для улучшения свойств проволоки или арматурных стержней.
Диаграмма растяжения (рис. 1.2) характеризует поведение конкретного образца, но отнюдь не обобщенные свойства материала. Для получения характеристик материала строится условная диаграмма напряжений, на которой откладываются относительные величины – напряжения σ=F/A0 и относительные деформации ε=Δl/l0 (рис. 1.3), где А0, l0 – начальные параметры образца.
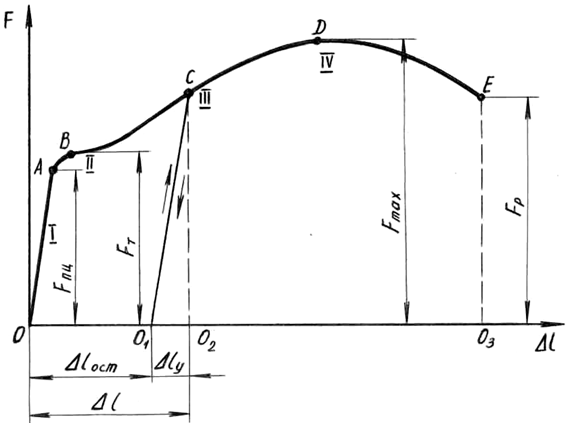
Рис. 1.2. Диаграмма растяжения образца из малоуглеродистой стали
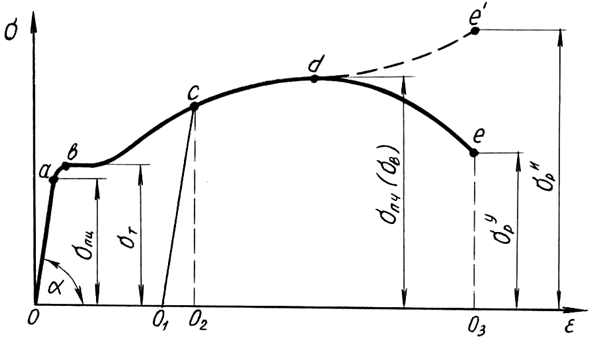
Рис. 1.3. Условная диаграмма напряжений при растяжении
Условная диаграмма напряжений при растяжении позволяет определить следующие характеристики материала (рис. 1.3):
σпц – предел пропорциональности – напряжение, превышение которого приводит к отклонению от закона Гука. После наклепа σпц может быть увеличен на 50-80%;
σу – предел упругости – напряжение, при котором остаточное удлинение достигает 0,05%. Напряжение σу очень близко к σпц и обнаруживается при более тонких испытаниях. В данной работе σу не устанавливается;
σт – предел текучести – напряжение, при котором происходит рост деформаций при постоянной нагрузке.
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют ≈0,2% (рис. 1.4);
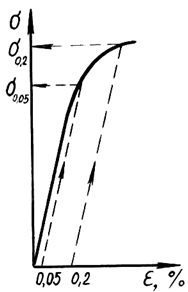
Рис. 1.4. Определение предела упругости и условного предела текучести
σпч (σв) – предел прочности (временное сопротивление) – напряжение, соответствующее максимальной нагрузке;
σр – напряжение разрыва. Определяется условное σур и истинное σир=Fр/Аш, где Аш – площадь сечения «шейки» в месте разрыва.
Определяются также характеристики пластичности – относительное остаточное удлинение
δ = (l1 – l0)∙100% / l0,
где l1 – расчетная длина образца после разрыва,
и относительное остаточное сужение
ψ = (А0 — Аш)∙100% / А0.
По диаграмме напряжений можно приближенно определить модуль упругости I рода
E=σпц/ε=tgα,
причем после операции наклепа σпц возрастает на 20-30%.
Работа, затраченная на разрушение образца W, графически изображается на рис. 1.2 площадью диаграммы OABDEO3. Приближенно эту площадь определяют по формуле:
W = 0,8∙Fmax∙Δlmax.
Удельная работа, затраченная на разрушение образца, говорит о мере сопротивляемости материала разрушению w = W/V, где V = A0∙l0 – объем рабочей части образца.
По полученным прочностным и деформационным характеристикам и справочным таблицам делается вывод по испытуемому материалу о соответствующей марке стали
Контрольные вопросы
- Изобразите диаграмму растяжения образца из малоуглеродистой стали (Ст.3). Покажите полные, упругие и остаточные абсолютные деформации при нагружении силой, большей, чем Fт.
- На каком участке образца происходят основные деформации удлинения? Как это наблюдается на образце? Какие нагрузки фиксируются в этот момент?
- Объясните, почему после образования шейки дальнейшее растяжение происходит при все уменьшающейся нагрузке?
- Перечислите механические характеристики, определяемые в результате испытаний материала на растяжение. Укажите характеристики прочности и пластичности.
- Дайте определение предела пропорциональности.
- Дайте определение предела упругости.
- Дайте определение предела текучести.
- Дайте определение предела прочности.
- Как определить предел текучести при отсутствии площадки текучести? Покажите, как это сделать, по конкретной диаграмме.
- Какие деформации называются упругими, какие остаточными? Укажите их на полученной в лабораторной работе диаграмме растяжения стали.
- Как определяется остаточная деформация после разрушения образца?
- Выделите на диаграмме растяжения образца из мягкой стали упругую часть его полного удлинения для момента действия максимальной силы.
- Какое явление называется наклепом? До какого предела можно довести предел пропорциональности материалов с помощью наклепа?
- Как определяется работа, затраченная на разрушение образца? О каком свойстве материала можно судить по удельной работе, затраченной на разрушение образца?
- Как определить марку стали и допускаемые напряжения для нее после проведения лабораторных испытаний?
- Чем отличается диаграмма истинных напряжений при растяжении от условной диаграммы?
- Можно ли определить модуль упругости материала по диаграмме напряжений?
- Как определить работу, затрачиваемую на деформации текучести лабораторного образца?
Испытание материалов на сжатие >
Краткая теория >
Примеры решения задач >
Источник
[c.15]
Важной характеристикой материала является удельная работа деформации, величину которой а находят как отношение полной работы к объему рабочей части образца
[c.136]
Разделив полную работу деформации А на объем рабочей части образца, получим удельную работу деформации, т. е. работу, затраченную на деформирование единицы объема материала
[c.98]
Удельная работа деформации в пределах упругости выражается площадью треугольника на диаграмме а — е (рис. 104, б).
[c.98]
Удельная работа деформации характеризует способность материала сопротивляться ударному действию нагрузки чем больше удельная работа деформации до разрыва, тем лучше материал сопротивляется ударным нагрузкам.
[c.98]
Площадь диаграммы напряжений а — ев соответствующем масштабе равна удельной работе деформации.
[c.99]
Удельной потенциальной энергией деформации называется работа деформации, приходящаяся на единицу объема бруса
[c.197]
Здесь А (втк) —. значение удельной работы деформации в истинном состоянии равновесия. Учитывая, что
[c.211]
Выражение (8.9), как известно из (4.36), представляет собой значение удельной работы деформации, соответствующее вариации вектора перемещения б и, и всегда положительно-определенно. Используя (4.20) и (8.7), второму члену (8.8) придадим вид
[c.212]
Рассмотрим теперь равновесие, при котором заданы перемещения Uh и соответствующий тензор напряжений Omh- При переходе от истинного напряженного состояния Omh к смежному Отк + Отк изменение удельной работы деформации будет
[c.213]
Функция W (ви) называется упругим потенциалом и представляет собой удельную работу деформации или удельную потенциальную энергию деформации. .
[c.54]
При анализе упругой зоны диаграммы напряжений (рис. 4.5.1) в точке Ь, разделив полную работу деформации А на объем рабочей части образца, вычислим удельную работу деформации, работу, затраченную на деформирование единицы объема материала
[c.58]
Удельная работа деформации в пределах упругости выражается площадью треугольника ОН на диаграмме а — е н равна удельной потенциальной энергии Зуп = и.
[c.58]
Воздух массой 1 кг при температуре — 25 С и давлении /j, =0,102 МПа адиабатно сжимается до давления р2 = 2 МПа. Определить удельные изменения внутренней энергии и энтальпии воздуха, работу деформации и располагаемую работу.
[c.26]
Способность материала сопротивляться ударам характеризуется величиной удельной работы деформации.
[c.36]
Полная удельная работа деформации представляет собою работу, затраченную на разрыв образца, отнесенную к единице объема,
[c.36]
Удельная работа деформации хрупких материалов мала. Этим объясняется слабое сопротивление таких материалов ударам и вообще динамическим нагрузкам.
[c.39]
Однако вязкость — это свойство тела сопротивляться деформации она измеряется силой, отнесенной к единицам длины и времени вязкость представляет собой не величину относительной деформации, а удельную работу деформации поэтому более обоснованно заменить термин ударная вязкость термином ударная прочность или сопротивление удару .
[c.12]
Если работу деформации отнести к единице объема, то получим удельную работу упругой деформации
[c.43]
Что называется удельной работой деформации Какова ее размерность
[c.49]
Деформация при растяжении или сжатии по двум взаимно перпендикулярным направлениям. Удельная работа деформации
[c.92]
Найдем теперь выражение удельной работы деформации при растяжении или сжатии по двум направлениям. Удельная работа деформации при растяжении (сжатии) в одном направлении выражается формулой
[c.95]
По полученным данным и формулам (11,2), (11,3) и (П,5) вычисляют характеристики прочности, а по формулам (11,7) и (П,8)—характеристики пластичности материала. Кроме того, определяют величину полной работы А, затраченной на деформацию образца, и по формуле (II, 9) вычисляют удельную работу деформации. Результаты заносят в журнал лабораторных работ.
[c.77]
Таким образом, при испытании любым остроконечным коническим или пирамидальным наконечником, а также по методу одностороннего сплющивания конических образцов твердость, вычисленная как удельная работа деформации в виде отношения работы деформирования к объему отпечатка, совпадает с твердостью, рассчитанной как среднее удельное давление в виде отношения вертикальной нагрузки к площади проекции отпечатка. Иначе говоря, твердость можно рассматривать и как среднее удельное давление, и как среднюю удельную работу деформирования. Первый способ удобен при измерении статической твердости, когда измеряется нагрузка, а второй — при расчете динамической твердости, когда известна энергия удара [30, 62].
[c.38]
Удельная работа деформации к моменту, когда в процессе нагружения образца напряжение достигает значения, соответствующего точке С в диаграмме напряжений, изображается площадью, заштрихованной вертикально на рис. 2.49, б. Если после этого производить разгрузку образца, то часть затраченной на деформацию работы, соответствующая упругим деформациям, возвращается. Указанная работа изображается площадью, заштрихованной горизонтально. Если разгрузка производится после того, как напряжение достигло величины меньшей, чем предел упругости, то, так как пути нагружения и разгрузки в этом случае совпадают, в процессе разгрузки (рис. 2.50, а) возвращается вся работа, затраченная на де( юрмацию образца.
[c.150]
Помимо так называемой средней удельной работы деформации а, которая пропорциональна общей работе А, вызвавшей
[c.66]
Величина средней удельной работы деформации а и работы а , расходуемой на деформацию образца до предела ползучести, в значительной степени зависит от скорости нагружения. Как следует из табл. 9 [3], эти значения изменяются в зависимости от скорости нагружения индивидуально для каждой пластмассы, поэтому нельзя вывести общую зависимость ударной прочности аморфных и кристаллических полимеров от скорости нагружения. Аналогичные выводы вытекают из табл. 10, составленной Винцентом [4], и из рабочих диаграмм, разработанных Ричардом [5], для некоторых аморфных и кристаллических полимеров (рис. 76, 77 и 78).
[c.68]
Средняя удельная работа деформации пластмасс растяжением при температуре 20°
[c.68]
Ударное испытание на растяжение не стандартизовано. Образцы, применяемые для определения удельной работы деформации, должны иметь достаточно резко ограниченный объём рабочей части, в противном случае затруднительно определить величину рабочего объёма. Переход от рабочей части к головкам выполняется в виде галтелей радиусом, равным 0,5—0,6 диаметра рабочей части образца.
[c.32]
При испытаниях определяются. удельная работа деформации
[c.32]
Обозначая удельную работу деформации варьированного состояния равновесия через A emh + 6enh) и разлагая ее выражение в ряд Тейлора, получим
[c.211]
Разложив выражение удельной работы деформации А( атк+ + 60nife) в ряд Тейлора, получим
[c.214]
Второй член правой части второго равенства (8.19), как это было и в (8.9), представляет собой удельную работу деформации, соответствующую вариации тензора напряжений бсттл, и всегда поло-жительно-определен.
[c.214]
Цилиндрическая винтовая пружина, изготовленная из 6-миллиметровой проволоки, имеет 20 витков со средним радиусом 7,5 см. Определить осевую растягивающую нагрузку, которая может быть допущена на пружину, если касательное напряжение в ней не должно превосходить 900 Kij M. Чему при этом будут равны удлинение пружины и наибольшая удельная работа деформации 0 = 8-10 кг см.
[c.99]
Равенство (5.5) представляет собой теорему Клапейрона для любого упругого тела. Здесь W — упругий потенциал, который при изотермическом деформировании определяется свободной энергией F = и — TflS и представляет собой удельную работу деформации.
[c.90]
Ударное испытание на изгиб образцов 10ХЮХ55 мм с надрезом (глубиной 2 мм и радиусом 1 мм) на маятниковом копре. Образцы быстро переносили из печи и помещали на опоры копра для испытаний. Метод производителен, так как испытания кратковременны, а в печи нагревали несколько образцов. Недостатки метода следующие а) удельная работа деформации не характеризует пластичность образцов, так как зависит и от прочности. Прочность металла понижается с повышением температуры, поэтому кривая температурной зависимости ударной вязкости показывает ошибочные (заниженные) значения температуры максимальной пластичности б) при переносе образца из печи и нахождении на опорах копра довольно значительно понижается температура, что зависит от температуры, скорости переноса и материала образца в) невозможность количественной оценки высокопластичных материалов, которые, не разрушаясь, проходят через опоры копра.
[c.13]
Материал Предел текучести в кГ/см Удлинение О-р в % Удельная работа деформации до а-р в кГсм1ст Предел прочности при разрыве в кГ см Относительное удлинение при разрыве в % Удельная работа деформации ДО °вр в кГсм/см Модуль упругости 10 в кГ/см
[c.67]
Удельная работа деформации а равна площади схематизированной диаграммы растяжения ОЗаЗ/1 (фиг. 21)
[c.15]
Краткий курс сопротивления материалов Издание 2
(1977) — [
c.61
,
c.108
]
Источник
Сопротивление материалов
Деформации при растяжении и сжатии
Продольные деформации при растяжении и сжатии
Характер деформаций, которым подвергается прямой брус при растяжении или сжатии мы определили, проведя опыт с резиновым брусом, на котором была нанесена сетка линий.
Теперь представим себе брус постоянного сечения имеющий длину l, один из концов которого защемлен, а к свободному концу приложена растягивающая сила F. Под действием этой силы брус удлинится на некоторую величину Δl, которую назовем абсолютным удлинением бруса.
Отношение абсолютного удлинения Δl к первоначальной длине бруса l назовем относительным удлинением и обозначим ε:
ε = Δl / l
Относительное удлинение – величина безразмерная, иногда его выражают в процентах.
Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.
***
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой линейной зависимостью, которая называется законом Гука, по имени английского физика Р. Гука (1653-1703 г.г.), установившего этот закон.
Сформулировать закон Гука можно так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.
Математически эта зависимость записывается так:
σ = E ε.
Здесь Е – коэффициент пропорциональности, который характеризует жесткость материала бруса, т. е. его способность сопротивляться деформации; его называют модулем продольной упругости, или модулем упругости первого рода.
Модуль упругости, как и напряжение, выражаются в паскалях (Па).
Значения Е для различных материалов устанавливаются экспериментально-опытным путем, и их величину можно найти в соответствующих справочниках.
Так, для стали Е = (1,96.…2,16) х 105 МПа, для меди Е = (1,00…1,30) х 105 МПа и т. д.
Следует оговориться, что закон Гука справедлив лишь в определенных пределах нагружения.
Если в формулу закона Гука подставить полученные ранее значения относительного удлинения и напряжения: ε = Δl / l , σ = N / А, то можно получить следующую зависимость:
Δl = Nl / (EА).
Произведение модуля упругости на площадь сечения Е×А, стоящее в знаменателе, называют жесткостью сечения при растяжении и сжатии; оно характеризует одновременно и физико-механические свойства материала бруса и геометрические размеры поперечного сечения этого бруса.
Приведенную выше формулу можно читать так: абсолютное удлинение или укорочение бруса прямо пропорционально продольной силе и длине бруса, и обратно пропорционально жесткости сечения бруса.
Выражение ЕА / l называют жесткостью бруса при растяжении и сжатии.
Приведенные выше формулы закона Гука справедливы лишь для брусьев и их участков, имеющих постоянное поперечное сечение, изготовленных из одного материала и при постоянной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами сечения, продольной силой, изменение длины всего бруса определяется, как алгебраическая сумма удлинений или укорочений отдельных участков:
Δl = Σ (Δli)
***
Поперечные деформации при растяжении и сжатии
Описанный ранее опыт с резиновым брусом, на котором нанесена сетка линий, показал, что при растяжении поперечные размеры бруса уменьшаются, а при сжатии – увеличиваются, т. е. брус становится либо тоньше, либо толще. Это явление характерно для брусьев, изготовленных из всех материалов.
Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций для данного материала – величина постоянная.
Впервые на эту зависимость указал французский ученый С. Пуассон (1781-1840 г.г.) и математически она записывается так:
|ε1| = ν |ε|,
где ν – коэффициент поперечной деформации, называемый коэффициентом Пуассона.
Коэффициент Пуассона является безразмерной величиной, и характеризует упругие свойства материала. При растяжении и сжатии этот коэффициент принимается одинаковым.
Значения коэффициента Пуассона для разных материалов установлены опытным путем и их величины можно найти в соответствующих справочниках.

***
Потенциальная энергия деформации при растяжении
При статическом (медленном) растяжении образца растягивающая сила F возрастает от нуля до какого-то значения, удлиняет образец на величину Δl и при этом совершает работу W.
Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми), можно считать, что W = U.
Путем изучения диаграмм растяжения образцов, установлено, что потенциальная энергия упругой деформации стержня длиной l постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна:
U = W = F Δl / 2 = N2 l / (2E А)
Сопротивление материалов оперирует, также, таким понятием, как удельная потенциальная энергия деформации, которая подсчитывается, как потенциальная энергия, приходящаяся на единицу объема бруса.
При одновременном действии растягивающих и сжимающих нагрузок или ступенчатом изменении размеров поперечного сечения бруса, его разбивают на однородные участки и для каждого подсчитывают потенциальную энергию деформации. Потенциальную энергию деформации всего бруса определяют, как сумму потенциальных энергий отдельных участков.
Анализируя формулу потенциальной энергии деформации можно сделать вывод, что эта величина всегда положительная, поскольку в ее выражения входят квадраты линейных и силовых величин. По этой причине при вычислении потенциальной энергии деформации нельзя применять принцип независимости действия сил (поскольку квадрат суммы не равен сумме квадратов слагаемых).
Единицей измерения потенциальной энергии деформации, как и работы, является джоуль (Дж).
***
Материалы раздела «Растяжение и сжатие»:
- Основные понятия о деформации растяжения и сжатия.
- Расчеты на прочность при растяжении и сжатии. Статически неопределимые задачи.
Смятие
Правильные ответы на вопросы Теста № 5
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 3 | 3 | 1 | 2 | 1 | 3 | 2 | 2 | 1 | 1 |
Источник
