Сжатие и растяжение вдоль оси y и вдоль оси x

3.1 Сжатие (растяжение) графика вдоль оси ординат
Рассмотрим
функцию вида y=A![]() ,
,
где A>0.
Нетрудно заметить, что при равных
значениях аргумента ординаты графика
этой функции будут в A
раз больше ординат графика функции
y=f(x)
при A>1
или в
![]() раз меньше ординат графика функцииy=f(x)
раз меньше ординат графика функцииy=f(x)
при A<1.
Таким образом, получаем следующее
правило.
Для
построения графика функции y=A![]()
следует построить график функции y=f(x)
и увеличить его ординаты в A
раз при A>1
(произвести растяжение графика вдоль
оси ординат) или уменьшить его ординаты
в
![]() раз приA<1
раз приA<1
(произвести сжатие графика вдоль оси
ординат). Полученный график является
графиком функции y=A![]() .
.
Пример
13. Построить
график функции y=2cos
x.
Р
е ш е н и е: Строим график функции y=cos
x
(рис.16 – пунктирная кривая) и растяжением
этого графика вдоль оси ординат в 2
раза получаем график функции y=2cos
x
(сплошная кривая).
Пример
14. Построить
график функции y=![]() x2.
x2.
Р
е ш е н и е: Строим график функции y=x2
и сжатием этого графика в 3 раза вдоль
оси ординат получаем график функции
y=![]() x2
x2
(рис.17).
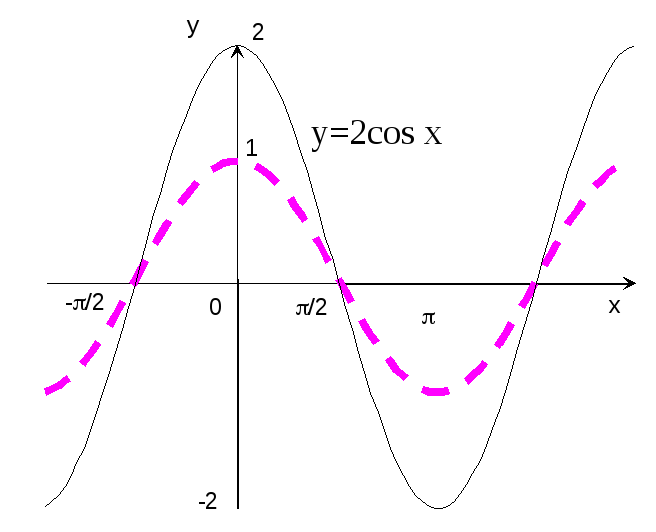
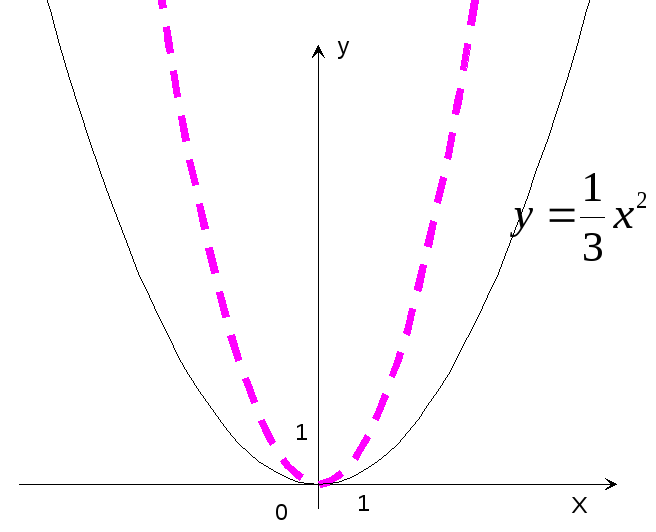
Рис.16
Рис.17
3.2. Сжатие (растяжение) графика вдоль оси абсцисс
Пусть
требуется построить график функции
y=f(x),
где >0.
Рассмотрим функцию y=f(x),
которая в произвольной точке x=x1
принимает значение y1=f(x1).
Очевидно,
что функция y=f(x)
принимает такое же значение в точке
x=x2,
координата
к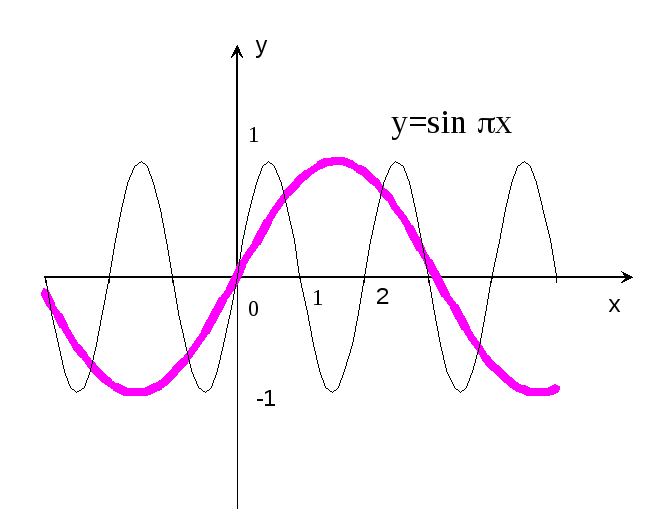 оторой
оторой
определяется равенствомx1=x2,
или x2=![]() ,
,
причём это равенство справедливо для
совокупности всех значений x
из области определения функции.
Следовательно, график функции y=f(x)
оказывается сжатым (при >1)
или растянутым (при <1)
вдоль оси абсцисс относительно графика
функции y=f(x).
Таким образом, получаем следующее
правило.
Для
построения графика функции y=f(x)
следует построить график функции y=f(x)
и уменьшить его абсциссы в
раз при >1
(произвести сжатие графика вдоль оси
абсцисс) или увеличить его абсциссы в
![]() раз при<1
раз при<1
(произвести растяжение графика вдоль
оси абсцисс). Полученный график является
графиком функции y=f(x).
П
Рис. 18
ример 15.Построить
график функции
![]() x.
x.
Р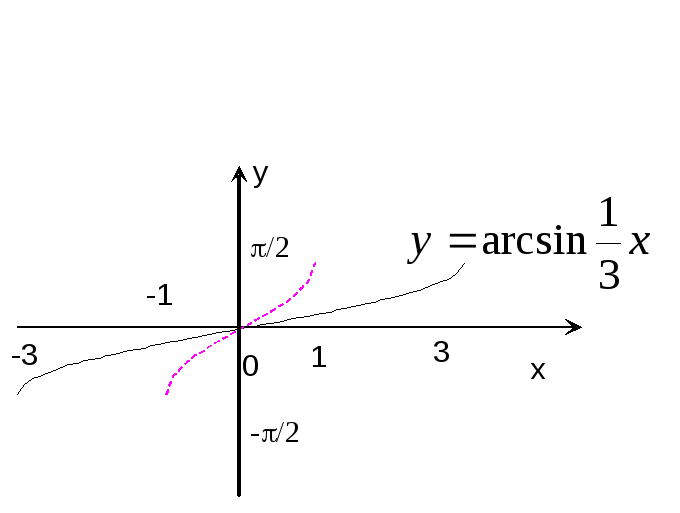 е ш е н и е: Строим график функции
е ш е н и е: Строим график функции
![]() x
x
(рис.18 – пунктирная кривая), и проводя
его сжатие в
раз вдоль оси абсцисс, получаем график
функции
![]() x
x
(сплошная кривая). Период этой функции
уже равен не 2,
а
![]() =2.
=2.
График пересекает ось абсцисс в точкахx=0,![]() …
…
.
Пример
16. Построить
график функции
![]() .
.
Р
е ш е н и е: Строим график функции
![]() и, растянув его вдоль оси абсцисс в 3
и, растянув его вдоль оси абсцисс в 3
раза, получаем график функции![]() .
.
4. Комбинация переноса, отражения и деформации
Рис.
19
Очень часто при построении графиков
функций применяют композицию приёмов,
изложенных в пунктах 1-3. Последовательное
применение ряда таких приёмов позволяет
существенно упростить построение
графика исходной функции и нередко
свести его в конце концов к построению
одной из простейших элементарных
функций.
Рассмотрим,
как с учётом изложенного следует,
например, построить
график функции вида y=Af(x+a)+b.
Запишем
исходную функцию в виде y=Af
[
( x+![]()
) ] +b
и схему поэтапного её упрощения
(последовательность преобразований):
1
 .y=Af
.y=Af
[
( x+![]()
) ] + b
; перенос оси абсцисс на b
единиц;
2
 .y=Af
.y=Af
[
( x+![]()
) ]; перенос оси ординат на
![]()
единиц;
3. y=Af
[
x
]; отражение графика относительно оси
абсцисс
( этап
этап
выполняется только приA<0);
4 .y=A·
.y=A·
f
(x); сжатие
или растяжение графика
вдоль оси ординат;
5. y=f
(x) отражение
графика относительно оси ординат
(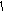 этап
этап
выполняется только при<0);
6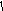 .y=f
.y=f
(
x); сжатие
или растяжение вдоль оси абсцисс;
7. y=f
( x);
Проводя
построение графика шаг за шагом в
порядке, обратном порядку упрощения
вида функции с учётом всех указанных
правил, получим график исходной функции.
Пример 17. Построить
график функции y=![]() .
.
Р
 е ш е н и е: Схема построения графика :
е ш е н и е: Схема построения графика :
y
 =
=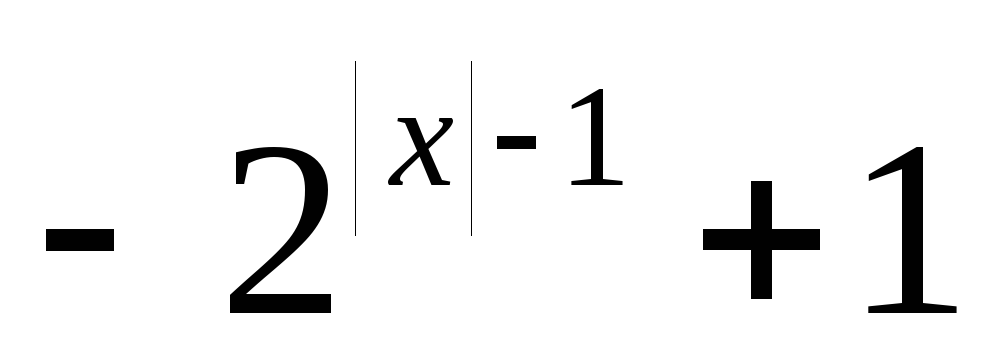
x
 0,
0,
y=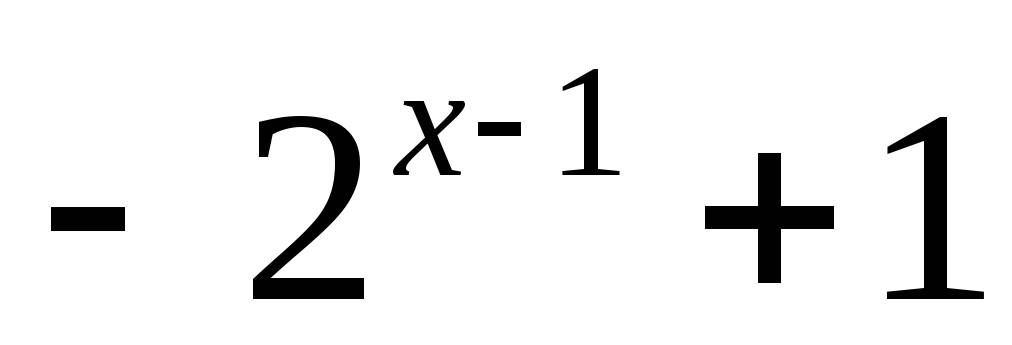 ;
;y=
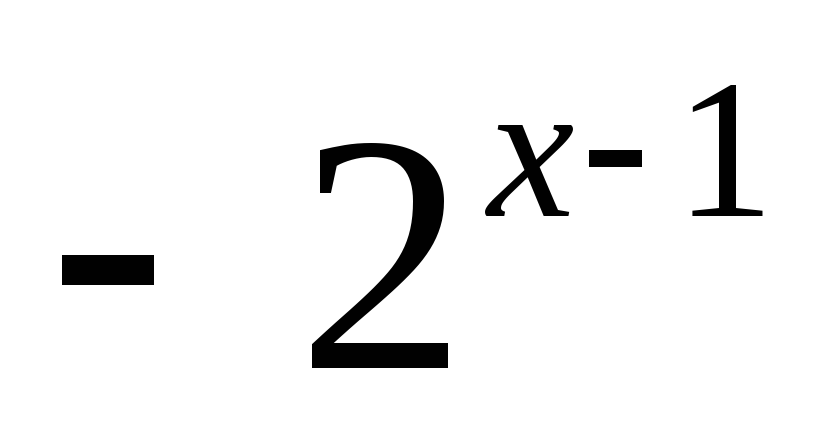 ;
;у=
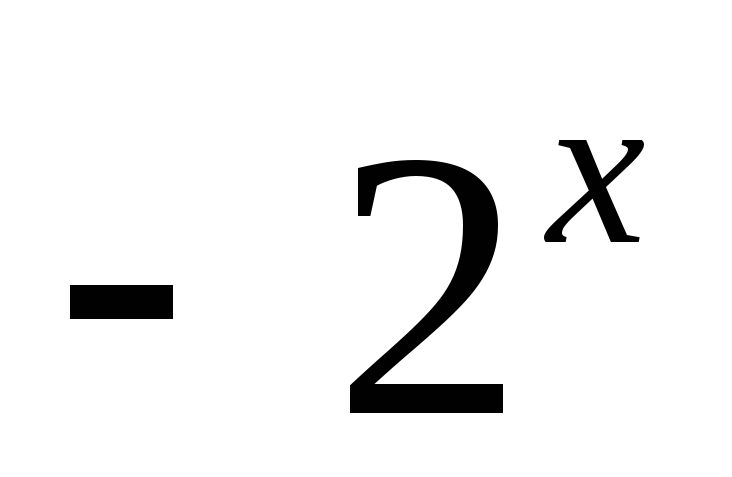 ;
;y=
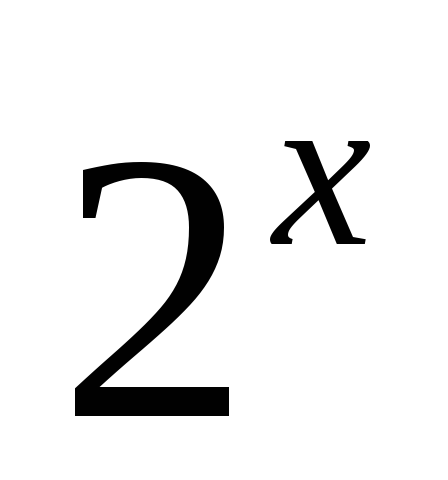 ;
;
Итак,
построение графика исходной функции
следует начинать с построения графика
функции y=![]() .
.
График (рис.20) пересекает ось ординат
в точке![]() (из условияx=0),
(из условияx=0),
а ось абсцисс в точках x=1
(из условия y=0,
т.е.![]() =0).
=0).
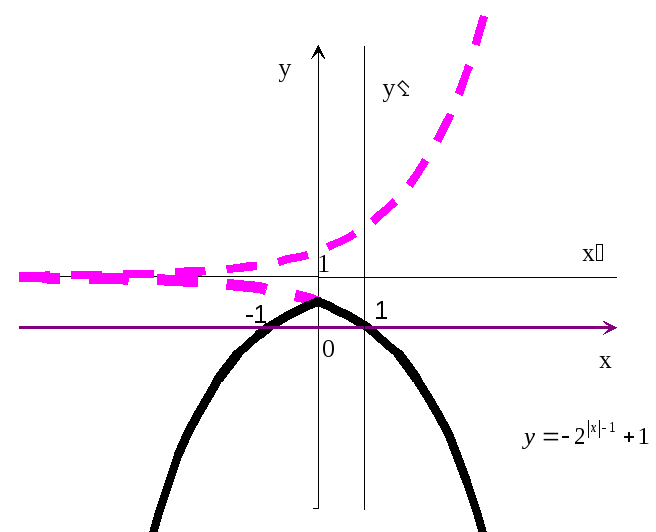 В
В
заключении отметим, что порядок упрощения
целесообразно проводить в следующей
последовательности.
Использование
чётности или нечётности функции.Перенос осей.
Отражение и
деформация.
Построение
же графика, как обычно, выполняется в
обратной последовательности.
Рис.20
Задание для
самостоятельного выполнения
Ниже
приводятся тексты заданий для
самостоятельного выполнения. Вам
необходимо построить графики функций,
оформить работу отдельно от решений по
другим предметам и выслать в адрес
Хабаровской краевой заочной
физико-математической школы.
М.11.2.1 С
помощью элементарных преобразований
постройте графики следующих функций:
y=x2-2;
y=(x+1)2;
y=sin
 x;
x;y=-
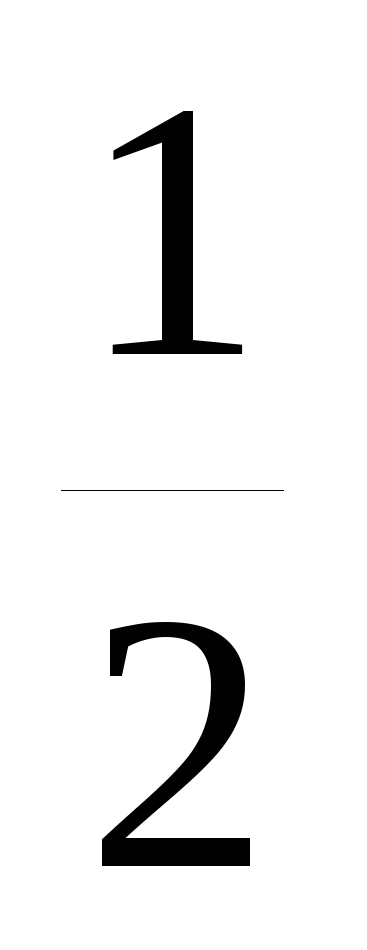
3sin x;y=tg
 ;
;
М.11.2.2.
Написать последовательность преобразований
и построить графики следующих функций:
y=
 ;
;y=(x-1)3+2;
y=ln
(1-x);y=tg(-
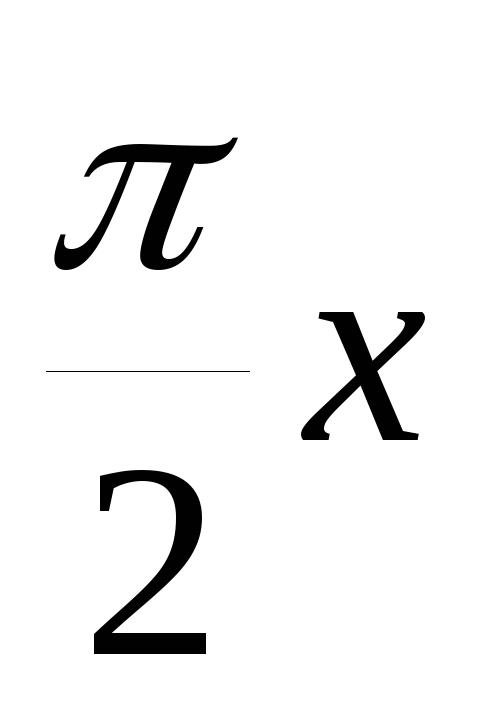 );
);y=
 cos(2x-1)-2.
cos(2x-1)-2.
Хабаровская краевая заочная
физико-математическая школа
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Самый наглядный способ представления информации – графический. Этот тезис применим и в математике. А при правильном подходе график может дать гораздо больше информации о поведении функции, чем просто положении точек на координатной плоскости.
Что может рассказать график $ y=f(x) $?
1. Область определения функции – значения аргумента $ x $, которые можно «подать на вход». Аргумент откладывается на горизонтальной оси.
2. Область значения функции – значения функции $ y $, получаемые «на выходе». Значения отмечаются на вертикальной оси.
3. Непрерывность функции. Для всех ли аргументов существуют значения?
4. Промежутки монотонности функции (возрастания или убывания).
Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции то есть $ x_{1}
Если же большему значению аргумента соответствует меньшее значение функции (то есть $ x_{1} y_{2} $), то функция называется убывающей.
Существуют функции, которые всегда возрастают (например, $ y=x^{3} $) или всегда убывают (например, $ y=-x $).
Но чаще функции имеют несколько промежутков возрастания и убывания. Например, функция $ y=x^{2} $ убывает при $ x in (0; +infty) $ и возрастает при $ x in (- infty; 0) $.
А график функции косинус имеет множество таких промежутков, сменяющих друг друга.
5. Точки минимума и максимума.
Значения аргумента, в которых функция перестает возрастать и начинает убывать, называются точками максимума. Если же в них, наоборот, функция перестает убывать и начинает возрастать – точками минимума. На графике $ y = sin(x) $ красным отмечены точки минимума, синим – максимума.
Всегда возрастающие и убывающие функции таких точек не имеют.
6. Ограниченность функции. Есть ли значения, за которые функция «не заходит»?
Функции могут быть неограниченными; ограниченными сверху, снизу, слева, справа, а также сразу с нескольких сторон.
Уже знакомая нам функция косинуса, например, ограничена и сверху, и снизу. Парабола $ y=x^{2} $ ограничена снизу. А график функции $ y=x^{3} $неограничен нигде.
7. Четность функции.
Функция называется четной, если выполняется равенство $ f(-x)=f(x) $. Такой функцией является парабола $ y=x^{2} $ так как верно, что $ -x^{2} = x^{2} $. Наглядным признаком четности является симметрия графика относительно оси ОY.
Если выполняется равенство $ f(-x)=-f(x) $, то функция считается нечетной. Примером такого типа функций может служить кубическая парабола $ y=x^{3} $ для которой $ (-x)^{3} = -x^{3} $. График нечетной функции будет симметричен относительно начала координат.
Не всякую функцию можно отнести одной из этих групп. Если не выполняется ни одно из названных условий, говорят, что функция не обладает четностью.
Рассмотрим функцию $ y = (x+2)^{2} $ и исследуем ее $ на четность.
$ y(-x) = (-x+2)^{2} = (-1(x-2))^{2} = (-1)^{2} cdot (x-2)^{2} = (x-2)^{2} $
Видно, что $ (x-2)^{2} neq (x+2)^{2} = y(x);$ и $ (x-2)^{2} neq -(x+2)^{2} = -y(x) $
То есть данная функция не является ни четной, ни нечетной.
8. Периодичность функции.
Если с какого-то момента график функции начинает повторяться, то такая функция называется периодичной. Таким свойством обладают все тригонометрические функции.
Помимо вышеназванных свойств у функций и их графиков есть особенные признаки, которые позволяют быстро и схематично их изобразить. Рассмотрим самые часто встречающиеся в математике зависимости.
Линейная функция
| Формула | $ y=kx+b, k neq 0 $ |
| График | |
| Особые свойства | $ k=tga $ тангенс угла наклона, $ b $ точка пересечения с $ OY $ |
| Область определения | $ R $ |
| Область значения | $ R $ |
| Непрерывность | да |
| Монотонность | $ k > 0 $ — возростает, $ k |
| Точки минимума и максимума | нет |
| Ограниченность | неограничено |
| Четность | нечетная |
| Периодичность | нет |
Квадратичная функция (парабола)
| Формула | $ y=ax^{2}+bx+c, a neq 0 $ |
| График |  |
| Особые свойства | $ a > 0 $ ветви направлены вверх, $ a |
| Область определения | $ R $ |
| Область значения | $ R $ |
| Непрерывность | да |
| Монотонность | При $ a > 0 (-infty;x_{вершины}) $ — убывает $ x_{вершины};+infty $ — возростает. При $ a |
| Точки минимума и максимума | $ a > 0 x_{вершины} $ — точка минимума, при $ a |
| Ограниченность | При $ a > 0 $ ограничена снизу, при $ a |
| Четность | $ b=0 $ — четная, $ b neq 0 $ — не обладает четностью |
| Периодичность | нет |
Кубическая парабола
| Формула | $ y=ax^{3}+b, a neq 0 $ |
| График | |
| Особые свойства | $ b $ — точка пересечения с $ OY $ |
| Область определения | $ R $ |
| Область значения | $ R $ |
| Непрерывность | да |
| Монотонность | При $ a > 0 $ — возростает, $ a |
| Точки минимума и максимума | нет |
| Ограниченность | Неограничена |
| Четность | $ b=0 $ — нечетная, иначе — не обладает четностью |
| Периодичность | нет |
Квадратный корень
| Формула | $ y=a sqrt {x}, a neq 0 $ |
| График | |
| Особые свойства | График располагается справа от нуля |
| Область определения | $ x geq 0 $ |
| Область значения | $ a geq 0 Rightarrow y geq 0 $ $ a leq 0 Rightarrow y leq 0 $ |
| Непрерывность | да |
| Монотонность | При $ a > 0 $ — возростает, $ a |
| Точки минимума и максимума | $ a > 0 — x = 0 $ точка минимума, $ a |
| Ограниченность | При $ a > 0 $ ограничена снизу и слева, при $ a |
| Четность | Не обладает четностью |
| Периодичность | нет |
Гипербола
| Формула | $ y= frac{k}{x}, k neq 0 $ |
| График | |
| Особые свойства | График имеет 2 асимптоты (прямые, к которым бесконечно приближается, но никогда не пересекает) $ x=0, y=0 $ |
| Область определения | $ x neq 0 $ |
| Область значения | $ y neq 0 $ |
| Непрерывность | Разрыв в точке $ x neq 0 $ |
| Монотонность | $ k > 0 $ убывает $ (-infty ; 0) $, возрастает $ (0;+infty) $ \ $ k |
| Точки минимума и максимума | нет |
| Ограниченность | Неограничена |
| Четность | Нечетная |
| Периодичность | Нет |
Окружность
| Формула | $ (x-a)^{2} + (y-b)^{2}= R^{2} $ |
| График | |
| Особые свойства | Центр окружности в точке $ a, b $, радиус $ R $ |
| Область определения | $ R $ |
| Область значения | $ R $ |
| Непрерывность | Да |
| Монотонность | |
| Точки минимума и максимума | нет |
| Ограниченность | С 4 сторон |
| Четность | При $ a=b=0 $ — четная, иначе не обладает четностью |
| Периодичность | Нет |
Показательная функция
| Формула | $ y=a^{x}, a > 0, a neq 1 $ |
| График | |
| Особые свойства | Все показательные функции проходят через точку (0,1) |
| Область определения | $ R $ |
| Область значения | $ (0;+infty) $ |
| Непрерывность | Да |
| Монотонность | $ a > 1 $ — возрастает, $ 0 |
| Точки минимума и максимума | нет |
| Ограниченность | Ограничена с низу |
| Четность | Не обладает четностью |
| Периодичность | Нет |
Логарифмическая функция
| Формула | $ y=log_{a}x, a > 0, a neq 1 $ |
| График | |
| Особые свойства | Все показательные функции проходят через точку (1,0) |
| Область определения | $ (0;+infty) $ |
| Область значения | $ R $ |
| Непрерывность | Да |
| Монотонность | $ a > 1 $ — возрастает, $ 0 |
| Точки минимума и максимума | нет |
| Ограниченность | Нет |
| Четность | Нет |
| Периодичность | Нет |
Синус
| Формула | $ y=sin(x) $ |
| График |  |
| Особые свойства | |
| Область определения | $ R $ |
| Область значения | [-1;1] |
| Непрерывность | Да |
| Монотонность | Да |
| Точки минимума и максимума | Точки минимума $ frac{pi}{2}+2pi k, kin Z $, точки минимума $ -frac{pi}{2}+2pi k, kin Z $ |
| Ограниченность | Сверху и снизу |
| Четность | Нечетная |
| Периодичность | Период $ 2pi $ |
Косинус
| Формула | $ y=cos(x) $ |
| График | |
| Особые свойства | |
| Область определения | $ R $ |
| Область значения | [-1;1] |
| Непрерывность | Да |
| Монотонность | Да |
| Точки минимума и максимума | Точки минимума $ 2pi k, kin Z $, точки минимума $ pi+2pi k, kin Z $ |
| Ограниченность | Сверху и снизу |
| Четность | Четная |
| Периодичность | Период $ 2pi $ |
Тангенс
| Формула | $ y=tgx $ |
| График | |
| Особые свойства | Имеет бесконечное число асимптот |
| Область определения | $ x neq frac{pi}{2}+pi k, kin Z $ |
| Область значения | $ R $ |
| Непрерывность | Разрыв в точках $ (-frac{pi}{2}+pi k; frac{pi}{2}+pi k), k in Z $ |
| Монотонность | Возрастает на каждом промежутке $ x neq frac{pi}{2}+pi k, kin Z $ |
| Точки минимума и максимума | Нет |
| Ограниченность | Нет |
| Четность | Четная |
| Периодичность | Период $ pi $ |
Котангенс
| Формула | $ y=ctgx $ |
| График | |
| Особые свойства | Имеет бесконечное число асимптот |
| Область определения | $ x neq pi k, kin Z $ |
| Область значения | $ R $ |
| Непрерывность | Разрыв в точках $ x = pi k, kin Z $ |
| Монотонность | Убывает на каждом промежутке $ (pi k, pi + pi k), k in Z $ |
| Точки минимума и максимума | Нет |
| Ограниченность | Нет |
| Четность | Нечетная |
| Периодичность | Период $ pi $ |
Преобразование графиков функции
График любой зависимости можно построить по точкам. Но в некоторых случаях гораздо проще преобразовать график какой-либо известной функции с помощью сдвигов, отражений и растяжений.
1. Симметрия относительно оси $ OX: f(x) rightarrow — f(x) $
Все абсциссы остаются неизменными, а все ординаты меняют знак на противоположный.
2. Симметрия относительно оси $ OY: f(x) rightarrow f(-x) $
Все ординаты графика остаются неизменными, а абсциссы меняют знак на противоположный.
При таком преобразовании четной функции, график остается неизменным.
3. Сдвиг вдоль оси $ OX: f(x) rightarrow f(x-a) $
Ординаты остаются неизменными, а абсциссам прибавляется $ a $. Если $ a > 0 $, то график сдвигается вправо, иначе – влево.
4. Сдвиг вдоль оси $ OY: f(x) rightarrow f(x)+b $
Абсциссы не меняются, а к ординатам прибавляется $ : b $. При $ b > 0 $ график сдвигается вверх, иначе – вниз.
Обратите внимание, что в пункте 3. перед $ a $ стоит знак «–», в то время как в 4. перед $ b $ стоит «+». При этом знаки параметров $ a,b $ могут быть любыми.
5. Сжатие и растяжение вдоль оси $ OX: f(x) rightarrow f(ax), a > 0 $
Ординаты остаются неизменными, а абсциссы делятся на $ a $. Точки пересечения графика функции с осью $ OY $ остаются на месте.
6. Сжатие и растяжение вдоль оси $ OY: f(x) rightarrow kf(x), k > 0 $
Абсциссы остаются неизменными, а ординаты умножаются на $ k $. Точки пересечения графика функции с осью $ OX $ остаются на месте.
7. Модуль функции: $ f(x) rightarrow|;f(x);| $
Точки с положительными ординатами остаются на месте, точки с отрицательными ординатами отбражаются симметрично относительно оси $ OX $.
8. Модуль аргумента: $ f(x) rightarrow f(|x|) $
Точки, соответствующие отрицательным абсциссами, стираются. Точки с положительными абсциссами остаются на месте, а так же отображаются симметрично относительно оси $ OY $. Функция становится четной.
Приведенные выше преобразования можно комбинировать и выполнять друг за другом.
Пример 1.
Построите график функции $ y=-2(x-3)^{2}+4 $.
Данный график можно получить из $ y=x^{2} $ последовательными сжатием вдоль оси $ OY $ в 2 раза, сдвигом вдоль оси $ OX $ на 3 вправо, сдвигом вдоль оси $ OY $ на 4 вверх и отражением относительно оси $ OX $.
Источник
Преобразования графиков: параллельный перенос, симметрия
В чистом виде основные элементарные функции встречаются, к сожалению, не так часто. Гораздо чаще приходится иметь дело с элементарными функциями, полученными из основных элементарных при помощи добавления констант и коэффициентов. Графики таких функций можно строить, применяя геометрические преобразования к графикам соответствующих основных элементарных функций (или переходить к новой системе координат).
С помощью геометрических преобразований графика функции f(x) может быть построен график любой функции вида ( pm {k_1} cdot f( pm {k_2} cdot (x + a)) + b,) где ({k_1},{k_2} > 0) — коэффициенты сжатия или растяжения (в зависимости от их значений) вдоль осей oy и ox соответственно. Знаки «минус» перед коэффициентами указывают на симметричное отображение графика относительно координатных осей, а и b определяют сдвиг относительно осей абсцисс и ординат соответственно.
Таким образом, различают три вида геометрических преобразований графика функции:
1. Первый вид — масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.
На необходимость масштабирования указывают коэффициенты k1 и k2, отличные от единицы, если (0 < {k_1} < 1,0 < {k_2} < 1) , то происходит сжатие графика относительно oy и растяжение относительно ox , если ({k_1},{k_2} > 1) , то производим растяжение вдоль оси ординат и сжатие вдоль оси абсцисс.
2. Второй вид — симметричное (зеркальное) отображение относительно координатных осей.
На необходимость этого преобразования указывают знаки «минус» перед коэффициентами k1 (в этом случае симметрично отображаем график относительно оси ox ) и k2 (в этом случае симметрично отображаем график относительно оси oy). Если знаков «минус» нет, то этот шаг пропускается.
3. Третий вид — параллельный перенос (сдвиг) вдоль осей ox и oy.
Это преобразование производится в последнюю очередь при наличии коэффициентов a и b, отличных от нуля. При положительном а график сдвигается влево на |а| единиц, при отрицательных а — вправо на |а| единиц. При положительном b график функции параллельно переносим вверх на |b| единиц, при отрицательном b — вниз на |b| единиц.
Рассмотрим примеры
Пример1
Построить графики функции (y = {x^2} — 10) и (y = {x^2} + 10) в одной координатной плоскости.
Построим для начала график функции (y = {x^2}) , это парабола с вершиной в точке (0;0) и ветвями вверх.
Для построения искомого графика функции (y = {x^2} — 10) необходимо параболу параллельно перенести в отрицательном направлении по У, т.е. вниз. Для построения искомого графика функции (y = {x^2} + 10) необходимо параболу параллельно перенести в положительном направлении по У, т.е. вверх.
Пример2
Построить графики функций (y = {left( {x + 2} right)^2}) и (y = {left( {x — 2} right)^2}) .
За основу возьмем тот же график параболы, но параллельный перенос будем осуществлять вдоль оси Ох. По правилу переноса график сдвинется влево на 2 единицы для функции (y = {left( {x + 2} right)^2}) . А для функции (y = {left( {x — 2} right)^2}) сдвиг произойдет вправо.
Пример3
Построить график функции (y = — {x^2}) .
За основу возьмем тот же график параболы. Производимое изменение графика носит название -отображение. Картинка получится симметричной исходной параболе, симметрия относительно Ох.
Пример4
Построить графики функций (y = left( {3{x^2}} right)) и (y = left( {frac{1}{3}{x^2}} right)) .
Для построения этих графиков произведем сжатие графика (y = {x^2}) для первой функции и растяжение – для второй.
Источник
