Сжатие и растяжение графиков функций вдоль оси оу

Анна Малкова
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее не постоянно хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.

1. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.

Теперь растяжение графика. Или сжатие.
2. Растяжение (сжатие) по горизонтали.
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в k раз по горизонтали, если , и сжат относительно исходного в k раз по горизонтали, если

3. Растяжение (сжатие) по вертикали
Пусть функция задана формулой и Тогда график функции растянут относительно исходного в М раз по вертикали, если , и сжат относительно исходного в М раз по вертикали, если

И отражение по горизонтали.
4. Отражение по горизонтали
График функции симметричен графику функции относительно оси Y.


5. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.

Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.
6. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.

Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.

Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.

Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.
Вот самые простые задачи на преобразование графиков.
1. Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
Вершина в точке

2. Построим график функции
Выделим полный квадрат в формуле.
График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка

Продолжение — в статье «Построение графиков функций».
Источник
Инфоурок
›
Алгебра
›Презентации›Простейшие преобразования графиков функций.(10 класс)
Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
Простейшие преобразования графиков функций. класс: 10 Б Учитель математики: Розметова Б.Е Тема урока:
2 слайд

Описание слайда:
Цели урока: Научить учащихся преобразованию графика функции с использованием параллельного переноса, растяжения, сжатия вдоль оси координат, а также применению всех перечисленных видов для одной функции. Способствовать развитию наблюдательности, умения анализировать, преобразовывать графики данных функций, побуждать учеников к самоконтролю своей учебной деятельности, научить сравнивать, делать выводы, находить аналогию. Воспитать умение строить, преобразовывать графики линейной функции, квадратичной функции и обратной пропорциональности. Воспитать такие качества личности, как познавательная активность, самостоятельность.
3 слайд

Описание слайда:
Вопросы на повторение: Графиком линейной функции является _______________ . Графиком квадратичной функции является _______________ . Если в квадратичной функции , коэффициент а >0, то ветви параболы направлены _______________ . Если в квадратичной функции , коэффициент а <0, то ветви параболы направлены _______________ . Если при решении квадратного уравнения D >0, то парабола пересекает ось Ох в _______ точках. Если при решении D=0, то точка пересечения параболы и оси Ох является _____________ параболы. Если при решении квадратного уравнения D <0, то парабола __________________ ось Ох. Значит, парабола расположена либо в _____________ полуплоскости, если а >0, либо в ______________ полуплоскости, если а <0 оси Оу. Графиком обратной пропорциональности является _________________ . Если k >0 в уравнении , то ветви гиперболы расположены в _____ четверти и в _____ четверти. Если k <0 в уравнении , то ветви гиперболы расположены в _____ четверти и _____ четверти.
4 слайд

Описание слайда:
Классная работа Простейшие преобразования графиков функций
5 слайд

Описание слайда:
Содержание темы: Параллельный перенос вдоль оси Оу. Растяжение и сжатие вдоль оси Оу. Параллельный перенос вдоль оси Ох. Растяжение и сжатие вдоль оси Ох. Преобразование графика функции с использованием всех четырех видов преобразования.
6 слайд

Описание слайда:
I. Параллельный перенос вдоль оси Оу График функции у=f(x)+d получаем из графика функции у=f(x) параллельным переносом на расстояние d вдоль оси Оу, в положительном направлении при d >0 и в отрицательном направлении при d <0.
7 слайд

8 слайд

Описание слайда:
II. Растяжение и сжатие вдоль оси Оу. График функции y=kf(x) получаем из графика функции y=f(x) при |k|> 1 растяжением в |k| раз вдоль оси Оу, а при 0 < |k| < 1 – сжатием в |k| раз вдоль оси Оу.
9 слайд

10 слайд

Описание слайда:
III. Параллельный перенос вдоль оси Ох. График функции у=f(x+b) получаем путем параллельного переноса графика функции у=f(x) вдоль оси Ох на |b| единиц в положительном направлении при b <0 и в отрицательном направлении – при b >0.
11 слайд

12 слайд

Описание слайда:
IV. Растяжение и сжатие вдоль оси Ох. График функции y=f(аx) получаем из графика функции y=f(x) сжатием в |a| раз вдоль оси Ох при |a| > 1 и растяжением в раз вдоль оси Ох при |a| < 1.
13 слайд

14 слайд

Описание слайда:
V. Преобразование графика функции с использованием всех четырех видов преобразования График функции y=kf(аx+b)+d получаем из графика функции y=f(x), используя все приведенные четыре вида преобразования.
15 слайд

Описание слайда:
Пример 5 Построим график функции: Решение: Сначала выделим полный квадрат для данного трехчлена:
16 слайд

Описание слайда:
Выполним следующие преобразования: построим график функции ; параболу параллельно перенесем вдоль оси Ох в положительном направлении на три единицы; полученную параболу растянем от оси Ох в 2 раза; затем к полученной параболе применим симметричность относительно прямой у=0; последнюю параболу параллельно перенесем вдоль оси Оу на одну единицу в отрицательном направлении.
17 слайд

Описание слайда:
y = x2 y = (x-3)2 y = 2(x-3)2 y = -2(x-3)2 y = -2(x-3)2-1
18 слайд

Описание слайда:
y = x y = 2x y = -3x y = x — 1,5 y = -2x + 3,5 Задание №19. Рядом с графиками напишите его функцию:
19 слайд

Описание слайда:
Задание №20. Рядом с данными функциями напишите каким цветом изображен ее график:
20 слайд

Описание слайда:
Расскажите о преобразованиях данных функций:
21 слайд

Описание слайда:
Задание №21. Какой кривой являются графики следующих функций:
22 слайд

Описание слайда:
Задание №22. Напишите рядом с графиками их функции:
23 слайд

Описание слайда:
Задание №23. С помощью шаблона графика функции построить график функции и рассказать о выполненных преобразованиях. Самостоятельная работа учащихся
24 слайд

Описание слайда:
Сначала выделим полный квадрат для данного трехчлена: Проверка самостоятельной работы:
25 слайд

26 слайд

Описание слайда:
Тестовые задания :
27 слайд

Описание слайда:
Правильные ответы:
28 слайд

Описание слайда:
Задание №26. С помощью графика определите, имеют ли графики функций общие точки:
29 слайд

30 слайд

Описание слайда:
§ 2 Простейшие преобразования графиков функций. Задания №24, №25 по учебнику. Домашнее задание:
Выберите книгу со скидкой:
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА
Инфолавка — книжный магазин для педагогов и родителей от проекта «Инфоурок»

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Краткое описание документа:
Научить учащихся преобразованию графика функции с использованием параллельного переноса, растяжения, сжатия вдоль оси координат, а также применению всех перечисленных видов для одной функции. Способствовать развитию наблюдательности, умения анализировать, преобразовывать графики данных функций, побуждать учеников к самоконтролю своей учебной деятельности, научить сравнивать, делать выводы, находить аналогию. Воспитать умение строить, преобразовывать графики линейной функции, квадратичной функции и обратной пропорциональности. Воспитать такие качества личности, как познавательная активность, самостоятельность.
Общая информация
Номер материала:
117268053056
Вам будут интересны эти курсы:
Оставьте свой комментарий
Источник
3.1 Сжатие (растяжение) графика вдоль оси ординат
Рассмотрим
функцию вида y=A![]() ,
,
где A>0.
Нетрудно заметить, что при равных
значениях аргумента ординаты графика
этой функции будут в A
раз больше ординат графика функции
y=f(x)
при A>1
или в
![]() раз меньше ординат графика функцииy=f(x)
раз меньше ординат графика функцииy=f(x)
при A<1.
Таким образом, получаем следующее
правило.
Для
построения графика функции y=A![]()
следует построить график функции y=f(x)
и увеличить его ординаты в A
раз при A>1
(произвести растяжение графика вдоль
оси ординат) или уменьшить его ординаты
в
![]() раз приA<1
раз приA<1
(произвести сжатие графика вдоль оси
ординат). Полученный график является
графиком функции y=A![]() .
.
Пример
13. Построить
график функции y=2cos
x.
Р
е ш е н и е: Строим график функции y=cos
x
(рис.16 – пунктирная кривая) и растяжением
этого графика вдоль оси ординат в 2
раза получаем график функции y=2cos
x
(сплошная кривая).
Пример
14. Построить
график функции y=![]() x2.
x2.
Р
е ш е н и е: Строим график функции y=x2
и сжатием этого графика в 3 раза вдоль
оси ординат получаем график функции
y=![]() x2
x2
(рис.17).
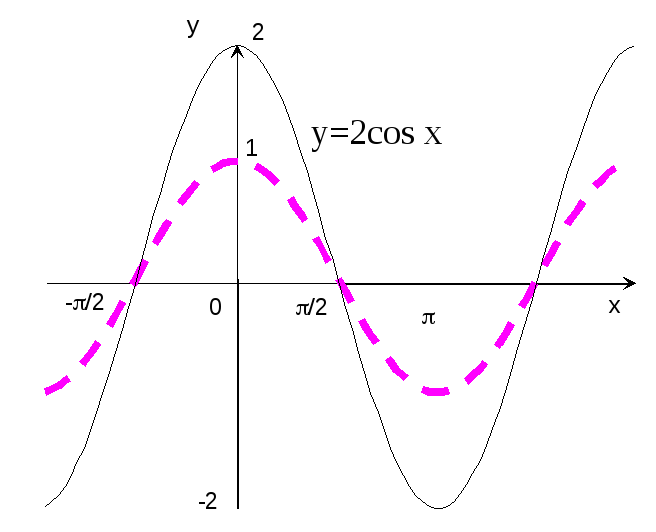
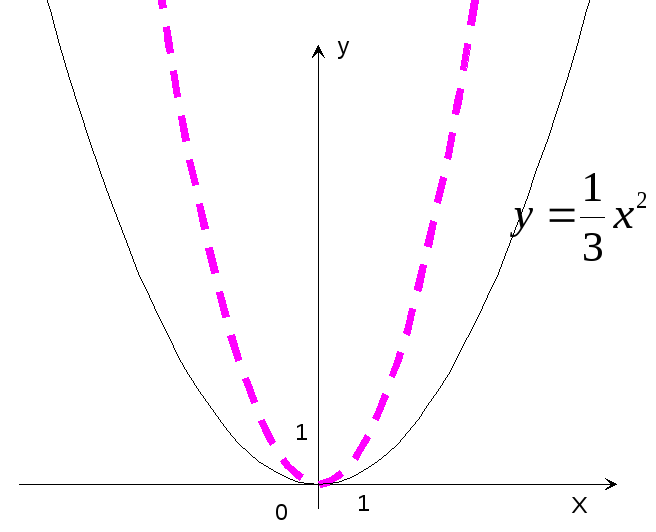
Рис.16
Рис.17
3.2. Сжатие (растяжение) графика вдоль оси абсцисс
Пусть
требуется построить график функции
y=f(x),
где >0.
Рассмотрим функцию y=f(x),
которая в произвольной точке x=x1
принимает значение y1=f(x1).
Очевидно,
что функция y=f(x)
принимает такое же значение в точке
x=x2,
координата
к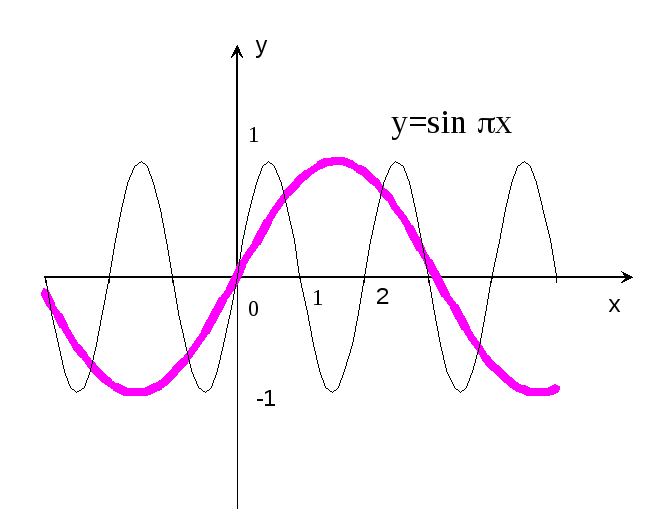 оторой
оторой
определяется равенствомx1=x2,
или x2=![]() ,
,
причём это равенство справедливо для
совокупности всех значений x
из области определения функции.
Следовательно, график функции y=f(x)
оказывается сжатым (при >1)
или растянутым (при <1)
вдоль оси абсцисс относительно графика
функции y=f(x).
Таким образом, получаем следующее
правило.
Для
построения графика функции y=f(x)
следует построить график функции y=f(x)
и уменьшить его абсциссы в
раз при >1
(произвести сжатие графика вдоль оси
абсцисс) или увеличить его абсциссы в
![]() раз при<1
раз при<1
(произвести растяжение графика вдоль
оси абсцисс). Полученный график является
графиком функции y=f(x).
П
Рис. 18
ример 15.Построить
график функции
![]() x.
x.
Р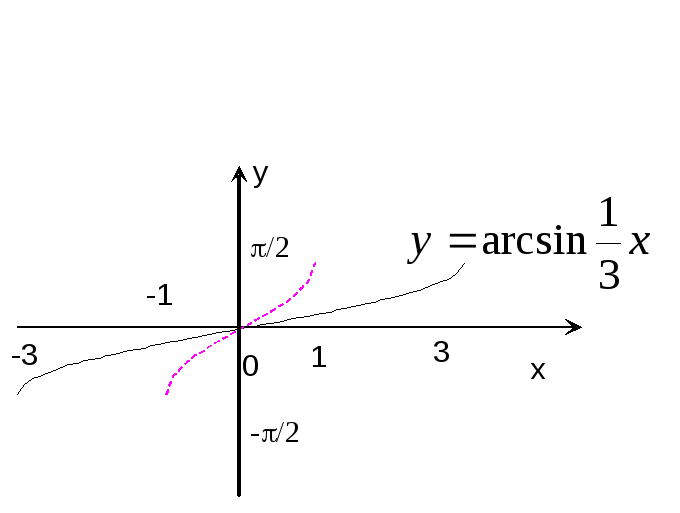 е ш е н и е: Строим график функции
е ш е н и е: Строим график функции
![]() x
x
(рис.18 – пунктирная кривая), и проводя
его сжатие в
раз вдоль оси абсцисс, получаем график
функции
![]() x
x
(сплошная кривая). Период этой функции
уже равен не 2,
а
![]() =2.
=2.
График пересекает ось абсцисс в точкахx=0,![]() …
…
.
Пример
16. Построить
график функции
![]() .
.
Р
е ш е н и е: Строим график функции
![]() и, растянув его вдоль оси абсцисс в 3
и, растянув его вдоль оси абсцисс в 3
раза, получаем график функции![]() .
.
4. Комбинация переноса, отражения и деформации
Рис.
19
Очень часто при построении графиков
функций применяют композицию приёмов,
изложенных в пунктах 1-3. Последовательное
применение ряда таких приёмов позволяет
существенно упростить построение
графика исходной функции и нередко
свести его в конце концов к построению
одной из простейших элементарных
функций.
Рассмотрим,
как с учётом изложенного следует,
например, построить
график функции вида y=Af(x+a)+b.
Запишем
исходную функцию в виде y=Af
[
( x+![]()
) ] +b
и схему поэтапного её упрощения
(последовательность преобразований):
1
 .y=Af
.y=Af
[
( x+![]()
) ] + b
; перенос оси абсцисс на b
единиц;
2
 .y=Af
.y=Af
[
( x+![]()
) ]; перенос оси ординат на
![]()
единиц;
3. y=Af
[
x
]; отражение графика относительно оси
абсцисс
( этап
этап
выполняется только приA<0);
4 .y=A·
.y=A·
f
(x); сжатие
или растяжение графика
вдоль оси ординат;
5. y=f
(x) отражение
графика относительно оси ординат
(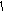 этап
этап
выполняется только при<0);
6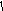 .y=f
.y=f
(
x); сжатие
или растяжение вдоль оси абсцисс;
7. y=f
( x);
Проводя
построение графика шаг за шагом в
порядке, обратном порядку упрощения
вида функции с учётом всех указанных
правил, получим график исходной функции.
Пример 17. Построить
график функции y=![]() .
.
Р
 е ш е н и е: Схема построения графика :
е ш е н и е: Схема построения графика :
y
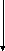
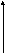 =
=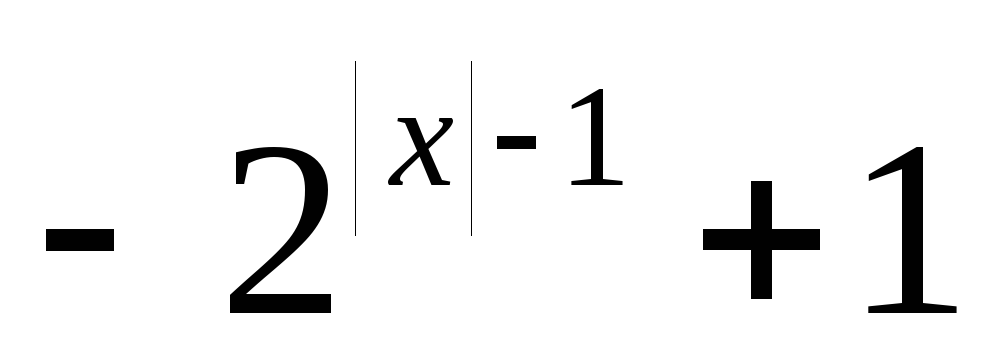
x
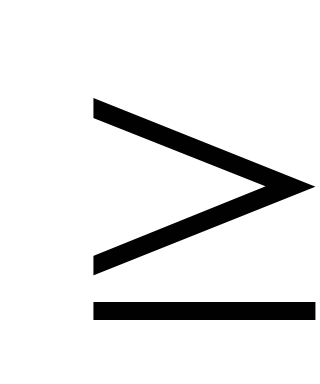 0,
0,
y=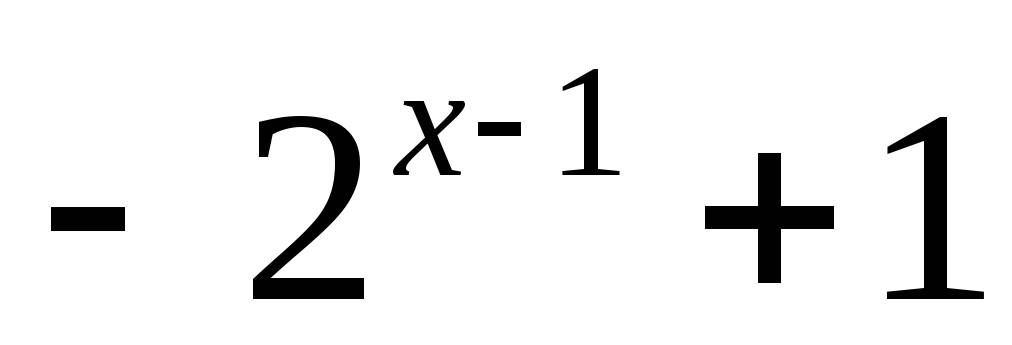 ;
;y=
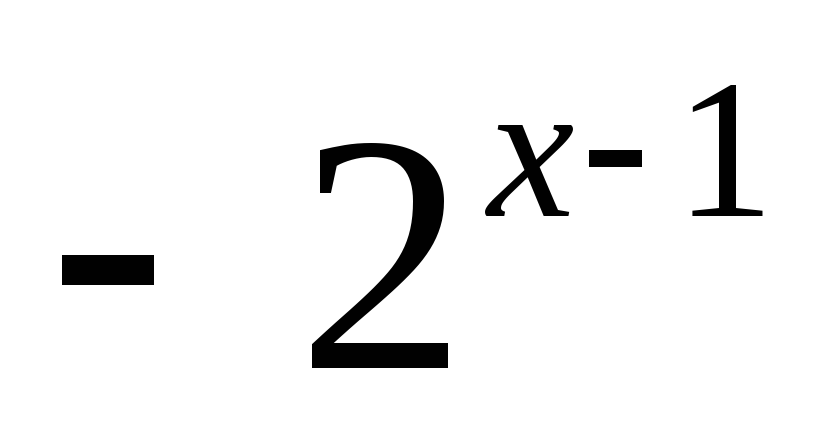 ;
;у=
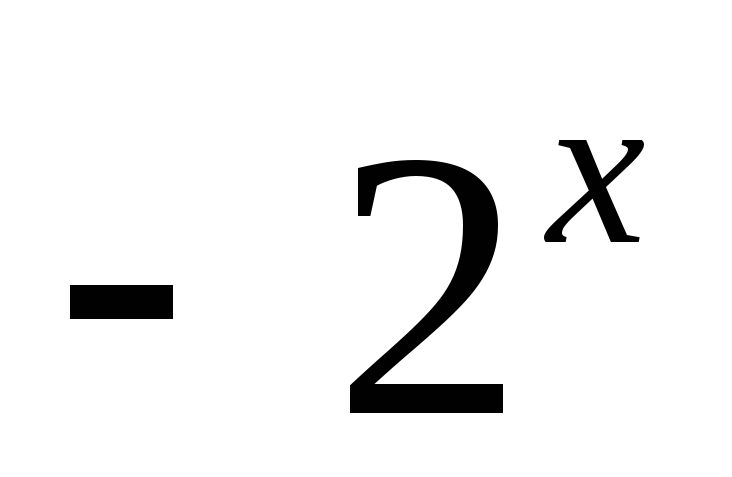 ;
;y=
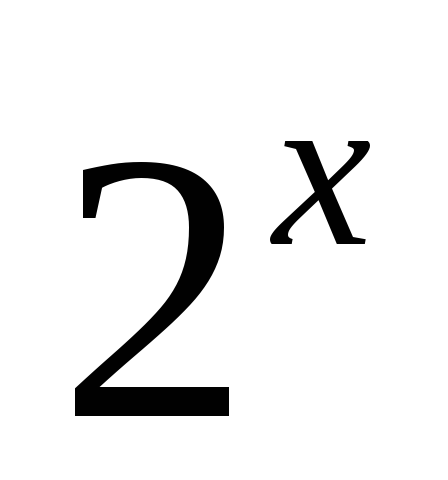 ;
;
Итак,
построение графика исходной функции
следует начинать с построения графика
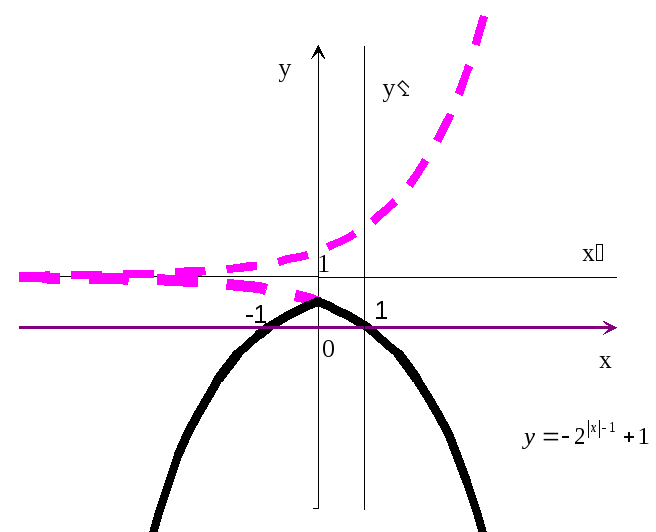
функции y=![]() .
.
График (рис.20) пересекает ось ординат
в точке![]() (из условияx=0),
(из условияx=0),
а ось абсцисс в точках x=1
(из условия y=0,
т.е.![]() =0).
=0).
 В
В
заключении отметим, что порядок упрощения
целесообразно проводить в следующей
последовательности.
Использование
чётности или нечётности функции.Перенос осей.
Отражение и
деформация.
Построение
же графика, как обычно, выполняется в
обратной последовательности.
Рис.20
Задание для
самостоятельного выполнения
Ниже
приводятся тексты заданий для
самостоятельного выполнения. Вам
необходимо построить графики функций,
оформить работу отдельно от решений по
другим предметам и выслать в адрес
Хабаровской краевой заочной
физико-математической школы.
М.11.2.1 С
помощью элементарных преобразований
постройте графики следующих функций:
y=x2-2;
y=(x+1)2;
y=sin
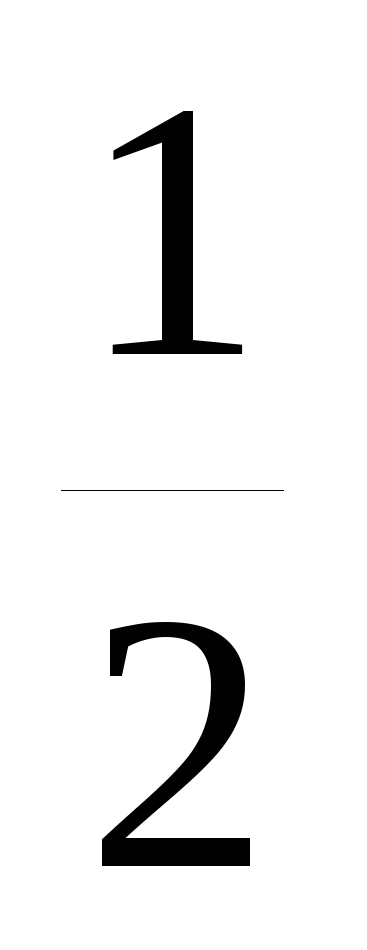 x;
x;y=-
3sin x;y=tg
 ;
;
М.11.2.2.
Написать последовательность преобразований
и построить графики следующих функций:
y=
 ;
;y=(x-1)3+2;
y=ln
(1-x);y=tg(-
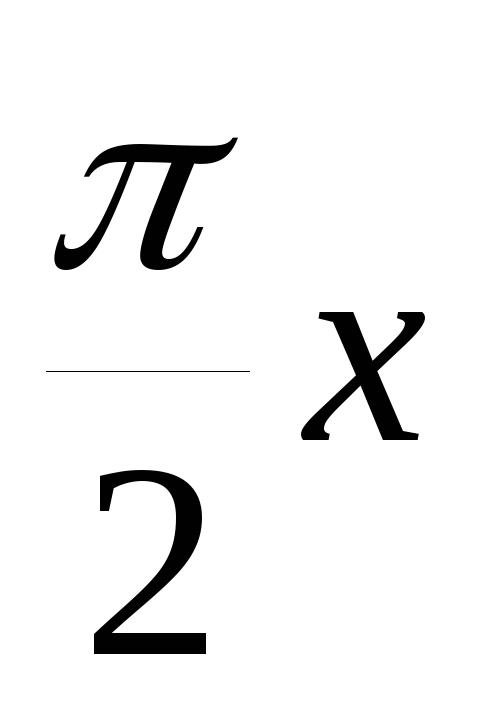 );
);y=
 cos(2x-1)-2.
cos(2x-1)-2.
Хабаровская краевая заочная
физико-математическая школа
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Если Вы знаете, как выглядят графики простейших элементарных функций, или умеете быстро строить их по характерным точкам, то сумеете также быстро построить на их основе графики более сложных функций того же класса. Для этого существуют правила преобразования графиков функций. Они легко запоминаются, но если Вы всё же не уверены в результате, проверьте его по одной-двум хорошим точкам. Эти правила, разумеется, общие для всех функций, а не только для тех, которые изучают в школе, поэтому известный график дальше будем называть заданным.
Пусть задан график функции y = f(x). Чтобы построить график функции
- y = mf(x), где m > 0 и m ≠ 1, нужно ординаты точек заданного графика умножить на m. Такое преобразование называется растяжением от оси x c коэффициентом m, если m > 1, и сжатием к оси x, если 0 < m < 1.
- y = −f(x) получается из графика функции f(x) преобразованием симметрии относительно оси x. (Преобразование симметрии — зеркальное отражение относительно прямой.)
- y = f(x) + n, получается из графика функции f(x) параллельным переносом последнего вдоль оси ординат на n единиц вверх, если n > 0 и, соответственно на |n| единиц вниз, если n
- y = f(kx), где k > 0 и k ≠ 1. Искомый график функции получается из заданного сжатием с коэффициентом k к оси y (если 0 < k < 1 указанное «сжатие» фактически является растяжением с коэффициентом 1/k)
- y = f(−x) получается из графика функции f(x) преобразованием симметрии относительно оси y
- y = f(x + l) получается из графика функции f(x) параллельным переносом последнего на l единиц влево, если l > 0 и, соответственно на |l| единиц вправо, если m < 0.
Например, пусть задан график функции y = √x_.

Чтобы построить графики других функций, содержащих аргумент (x) под знаком квадратного корня, воспользуемся перечисленными выше правилами. Заданный график повторим во вновь начерченных осях «карандашом бледно», требуемый график, который получится после преобразований, сделаем более интенсивным. В тетради лишнее можно будет удалить ластиком, останется только результат выполнения задания.
| Пример 1a. Построить график функции y = 2√x_
Растянули в 2 раза от оси x. Ордината каждой точки увеличилась в 2 раза. | Пример 1b. Построить график функции y = √x_ /2
Сжали вдвое к оси x. Ордината каждой точки уменьшилась в 2 раза. |
| Пример 3a. Построить график функции y = √x_ + 2
Параллельно перенесли на 2 единицы вверх вдоль оси y. Ордината каждой точки увеличилась на 2. | Пример 3b. Построить график функции y = √x_ − 2 |




