Свойства при растяжении металлов
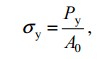
Испытание на растяжение металла заключаются в растяжении образца с построением графика зависимости удлинения образца (Δl) от прилагаемой нагрузки (P), с последующим перестроением этой диаграммы в диаграмму условных напряжений (σ — ε)
Испытания на растяжение проводятся по ГОСТ 1497, по этому же ГОСТу определяются и образцы на которых проводятся испытания.
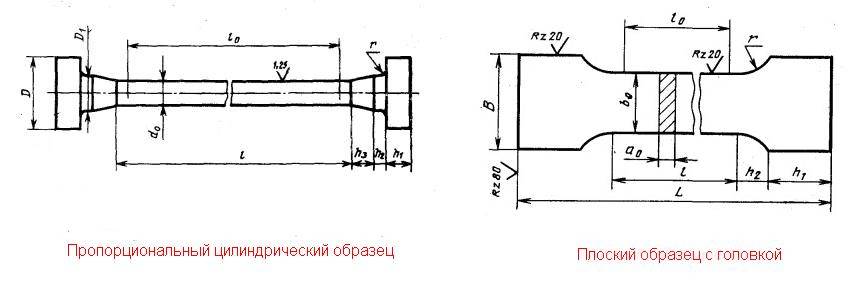 Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:
- Участок ОА — участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
- Участок ОВ — участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении
Выше точки В диаграмма растяжения отходит от прямой — деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.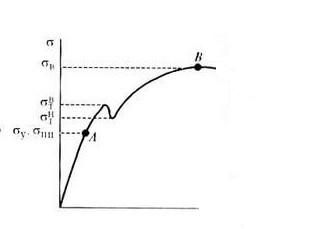 Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.
После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение — шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.
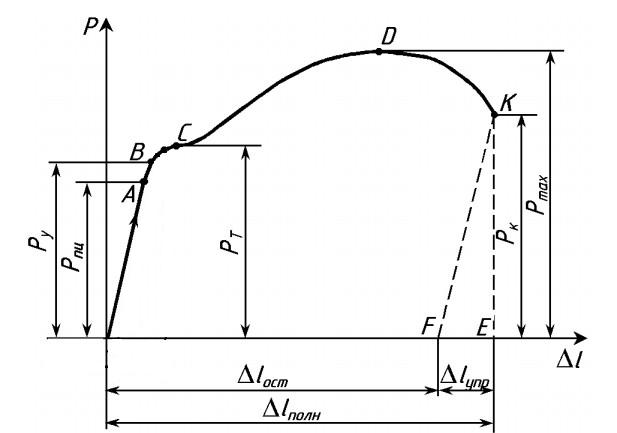
Прилагаемая нагрузка для растяжения образца зависит от геометрии этого образца. Чем больше площадь сечения, тем более высокая нагрузка необходима для растяжения образца. По этой причине, получаемая машинная диаграмма не дает качественной оценки механических свойств материала. Чтобы исключить влияние геометрии образца, машинную диаграмму перестраивают в координатах σ − ε путем деления ординат P на первоначальную площадь сечения образца A0 и абсцисс ∆l на lо. Перестроенная таким образом диаграмма называется диаграммой условных напряжений. Уже по этой, новой диаграмме, определяют механические характеристики материала.
Определяются следующие механические характеристики:
Предел пропорциональности σпц – наибольшее напряжение, после которого нарушается справедливость закона Гука σ = Еε , где Е – модуль продольной упругости, или модуль упругости первого рода. При этом Е =σ/ε = tgα , т. е. модуль E это тангенс угла наклона прямолинейной части диаграммы к оси абсцисс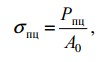
Предел упругости σу — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σу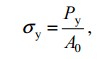
Предел текучести σт – напряжение, при котором происходит увеличение деформации без заметного увеличения растягивающей нагрузки
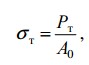 Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести
Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести
Предел прочности (временное сопротивление разрыву) σв – напряжение, соответствующее наибольшей нагрузке Pmax , предшествующей разрыву образца
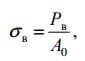
Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности — относительное удлинение δ и относительное сужение ψ
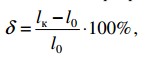
где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца
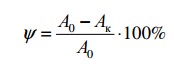

Изопропиловый спирт цена за тонну оптом — https://www.dcpt.ru
Источник
Машина для испытаний на растяжение с электромеханическим приводом
Статическое растяжение — одно из наиболее распространённых видов испытаний для определения механических свойств материалов.
Основные характеристики, определяемые при испытании[править | править код]
При статическом растяжении, как правило, определяются следующие характеристики материала.
- Характеристики прочности:
- предел пропорциональности,
- предел текучести,
- предел прочности (временное сопротивление разрушению),
- истинное сопротивление разрыву.
- Характеристики пластичности:
- относительное остаточное удлинение,
- относительное остаточное сужение.
- Характеристики упругости:
- модуль упругости (модуль Юнга).
- Прочие характеристики:
- коэффициент механической анизотропии
- коэффициент (модуль) упрочнения
Основные типы материалов[править | править код]
Принято разделять пластичные и хрупкие материалы. Основное отличие состоит в том, что первые деформируются в процессе испытаний с образованием пластических деформаций, а вторые практически без них вплоть до своего разрушения. За критерий для условной классификации материалов можно принять относительное остаточное удлинение δ = (lк − l0)/l0, где l0 и lк — начальная и конечная длина рабочей части образца), обычно вычисляемое в процентах. В соответствии с величиной остаточного удлинения материалы можно разделить на:
- пластичные (δ ≥ 10 %);
- малопластичные (5 % < δ < 10 %);
- хрупкие (δ ≤ 5 %).
Существующие материалы могут быть изотропными или анизотропными. В последнем случае из-за различия характеристик в различных направлениях необходимо произвести не одно, а несколько испытаний.
Образцы для испытаний на статическое растяжение[править | править код]
Цилиндрический пятикратный образец
Цилиндрический пятикратный образец после разрушения
Для испытаний на статическое растяжение используют образцы как с круглым, так и с прямоугольным сечением. Предъявляются повышенные требования к изготовлению образцов, как с точки зрения геометрии, так и с точки зрения обработки резанием. Требуется высокая однородность диаметра образца по его длине, соосность и высокое качество поверхности (малая шероховатость, отсутствие царапин и надрезов). При изготовлении образцов следует избегать перегрева материала и изменений его микроструктуры.
Образцы круглого сечения, как правило, имеют рабочую длину, равную четырём или пяти диаметрам — т. н. короткие образцы или десяти диаметрам — т. н. нормальные образцы. Перед началом испытания замеряется диаметр образца (обычно 6, 10 или 20 мм) для вычисления напряжения σ и для расчёта относительного остаточного сужения после разрушения образца. В случае использования экстензометра, длина рабочей части образца не замеряется, а деформация ε и относительное удлинение при разрушении регистрируются автоматически с помощью компьютера или измеряются по диаграмме σ — ε. При отсутствии экстензометра (не рекомендуется стандартом), отмечается рабочая длина образца, деформация ε рассчитывается по перемещениям конца образца (захвата), а относительное удлинение при разрушении рассчитывается путём замера разрушенного образца.
Диаграмма растяжения пластичного материала[править | править код]
Рис. 1. Типичная диаграмма σ — ε для малоуглеродистой стали
1. Предел прочности (временное сопротивление разрушению)
2. Предел текучести (верхний)
3. Точка разрушения
4. Область деформационного упрочнения
5. Образование шейки на образце
Рис. 2. Типичная диаграмма σ — ε для алюминиевых сплавов
1. Предел прочности (временное сопротивление разрушению)
2. Условный предел текучести (σ0.2)
3. Предел пропорциональности
4. Точка разрушения
5. Деформация при условном пределе текучести (обычно, 0,2 %)
Микроструктура доэвтектоидной стали (0,7 % углерода)
Обычно диаграмма растяжения является зависимостью приложенной нагрузки P от абсолютного удлинения Δl. Современные машины для механических испытаний позволяют записывать диаграмму в величинах напряжения σ (σ = P/A0, где A0 — исходная площадь поперечного сечения) и линейной деформации ε (ε = Δl/l0 ). Такая диаграмма носит название диаграммы условных напряжений, так как при этом не учитывается изменение площади поперечного сечения образца в процессе испытания.
Начальный участок является линейным (т. н. участок упругой деформации). На нём действует закон Гука:
Затем начинается область пластической деформации. Эта деформация остаётся и после снятия приложенной нагрузки. Переход в пластическую область обнаруживается не только по проявлению остаточных деформаций, но и по уменьшению наклона кривой с увеличением степени деформации. Данный участок диаграммы обычно называют площадкой (зоной) общей текучести, так как пластические деформации образуются по всей рабочей длине образца. С целью изучения и точного анализа диаграммы деформации, современные испытательные машины оснащены компьютеризированной записью результатов.
По наклону начального участка диаграммы рассчитывается модуль Юнга. Для малоуглеродистой стали наблюдается т. н. «зуб текучести» и затем площадка предела текучести. Явление «зуба» текучести связано с дислокационным механизмом деформации. На начальном участке плотность дислокаций является недостаточной для обеспечения более высокой степени деформации. После достижения точки верхнего предела текучести начинается интенсивное образование новых дислокаций, что приводит к падению напряжения. Дальнейшая деформация при пределе текучести происходит без роста напряжения . Зависимость предела текучести, от размера зерна, d, выражена соотношением Холла-Петча:
После достижения конца площадки текучести (деформация порядка 2 — 2,5 %) начинается деформационное упрочнение (участок упрочнения), видимое на диаграмме, как рост напряжения с ростом деформации. В этой области до достижения максимальной нагрузки (напряжения (σВ) макродеформация остаётся равномерной по длине испытуемого образца. После достижения точки предела прочности начинает образовываться т. н. «шейка» — область сосредоточенной деформации. Расположение «шейки» зависит от однородности геометрических размеров образца и качества его поверхности. Как правило, «шейка» и, в конечном счёте, место разрушения расположено в наиболее слабом сечении. Кроме того, важное значение имеет одноосность напряжённого состояния (отсутствие перекосов образца в испытательной машине). Для пластичных материалов при испытании на статическое растяжение одноосное напряжённое состояние сохраняется лишь до образования т. н. «шейки» (до достижения максимальной нагрузки и начала сосредоточенной деформации).
Вид диаграммы деформации, приведённый на рис. 1 является типичным для О.Ц.К. материалов с низкой исходной плотностью дислокаций.
Для многих материалов, например, с Г. Ц. К. кристаллической решёткой, а также для материалов с высокой исходной плотностью дефектов, диаграмма имеет вид, показанный на рис. 2. Основное отличие — отсутствие явно выраженного предела текучести. В качестве предела текучести выбирается значение напряжения при остаточной деформации 0,2 % (σ0.2).
После достижения максимума нагрузки происходит падение нагрузки (и, соответственно, напряжения σ) за счёт локального уменьшения площади поперечного сечения образца. Соответствующий (последний) участок диаграммы называют зоной местной текучести, так как пластические деформации продолжают интенсивно развиваться только в области шейки.
Иногда используется диаграмма истинных напряжений, S — e (истинное напряжение S = P/A, где A — текущая площадь поперечного сечения образца; истинная деформация e = ln(l+Δl/l), где l — текущая длина образца). В этом случае, после достижения максимальной нагрузки не происходит падения напряжения, истинное напряжение растёт за счёт локального уменьшения сечения в «шейке» образца. Поэтому различие между диаграммами истинных и условных напряжений наблюдается только после предела прочности — до точки 1 они практически совпадают друг с другом.
Образцы из пластичного материала разрушаются по поперечному сечению с уменьшением диаметра в месте разрыва из-за образования «шейки».
Диаграмма растяжения хрупкого материала[править | править код]
Диаграмма растяжения и диаграмма условных напряжений хрупких материалов по виду напоминает диаграмму, показанную на рис. 2 за тем исключением, что не наблюдается снижения нагрузки (напряжения) вплоть до точки разрушения. Кроме того, данные материалы не получают таких больших удлинений как пластичные и по времени разрушаются гораздо быстрее. На диаграмме хрупких материалов уже на первом участке имеется ощутимое отклонение от прямолинейной зависимости между нагрузкой и удлинением (напряжением и деформацией), так что о соблюдении закона Гука можно говорить достаточно условно. Так как пластических деформаций хрупкий материал не получает, то в ходе испытания не определяют предела текучести. Не имеет особенного смысла также рассчитывать и относительное сужение образца, так как шейка не образуется и диаметр после разрыва практически не отличается от исходного.
Влияние скорости деформации и температуры на прочностные характеристики[править | править код]
Стандарты на проведение испытаний на статическое растяжение, как правило, ограничивают скорость деформации или скорость приложения нагрузки. Так, стандарт ASTM E-8 ограничивает скорость деформации величиной 0,03 — 0,07 мм/мин. Такое ограничение вызвано искажением результатов за счёт повышения прочности металлов с ростом скорости деформации (при постоянной температуре). При скоростях деформации до 1 сек скорость деформации практически не влияет на прочностные характеристики (в частности, на предел текучести) (источник???).
В общем виде можно выразить формулу влияния скорости деформации на предел текучести в виде:
где — скорость деформации; — астотный фактор, — активационный объём; — напряжение течения; — экстраполяция напряжения течения на нулевую скорость деформации.
Эта же зависимость даёт и зависимость напряжения течения от температуры. В области низких температур и при отсутствии фазовых превращений прочность кристаллических материалов повышается. Вклад в повышение прочности даёт и переход от термически активируемого процесса деформации за счёт движения дислокаций к механизму деформации путём двойникования.
Стандарты на проведение испытаний[править | править код]
- ГОСТ 6996-66
- ГОСТ 1497-84 Металлы. Методы испытаний на растяжение
- ГОСТ 11262-80 (СТ СЭВ 1199-78) Пластмассы. Метод испытания на растяжение
- ASTM E-8 и ASTM E-8M
Литература[править | править код]
- Я. Б. Фридман. Механические свойства металлов. 3-е изд. В 2-х ч. М.: Машиностроение, 1974
- М. Л. Бернштейн, В.А Займовский. Механические свойства металлов. 2-е изд. М.: Металлургия, 1979.
- А. Н. Васютин, А. С. Ключ. Влияние температуры и скорости деформации на сопротивление деформированию малоуглеродистых и низколегированных сталей. Заводская лаборатория, 1985, № 4.
См. также[править | править код]
- Растяжение-сжатие
Источник
РоÑновнÑм меÑ
аниÑеÑким
ÑвойÑÑвам
меÑаллов оÑноÑÑÑÑÑ Ð¿ÑоÑноÑÑÑ,
вÑзкоÑÑÑ, плаÑÑиÑноÑÑÑ,
ÑвеÑдоÑÑÑ, вÑноÑливоÑÑÑ, ползÑÑеÑÑÑ, изноÑоÑÑойкоÑÑÑ. Ðни
ÑвлÑÑÑÑÑ Ð³Ð»Ð°Ð²Ð½Ñми Ñ
аÑакÑеÑиÑÑиками меÑалла или
Ñплава.
РаÑÑмоÑÑим некоÑоÑÑе ÑеÑминÑ, пÑименÑемÑе пÑи Ñ
аÑакÑеÑиÑÑике меÑ
аниÑеÑкиÑ
ÑвойÑÑв. ÐÐ·Ð¼ÐµÐ½ÐµÐ½Ð¸Ñ ÑазмеÑов и ÑоÑмÑ, пÑоиÑÑ
одÑÑие в ÑвеÑдом Ñеле под дейÑÑвием
внеÑниÑ
Ñил, назÑваÑÑÑÑ Ð´ÐµÑоÑмаÑиÑми, а пÑоÑеÑÑ, иÑ
вÑзÑваÑÑий,â
деÑоÑмиÑованием. ÐеÑоÑмаÑии, иÑÑезаÑÑие пÑи ÑазгÑÑзке, назÑваÑÑÑÑ ÑпÑÑгими, а не
иÑÑезаÑÑие поÑле ÑнÑÑÐ¸Ñ Ð½Ð°Ð³ÑÑзки â оÑÑаÑоÑнÑми или плаÑÑиÑеÑкими.
ÐапÑÑжением назÑваеÑÑÑ Ð²ÐµÐ»Ð¸Ñина внÑÑÑенниÑ
Ñил,
возникаÑÑиÑ
в ÑвеÑдом Ñеле под влиÑнием внеÑниÑ
Ñил.
Ðод пÑоÑноÑÑÑÑ Ð¼Ð°ÑеÑиала понимаÑÑ ÐµÐ³Ð¾ ÑпоÑобноÑÑÑ ÑопÑоÑивлÑÑÑÑÑ
деÑоÑмаÑии или ÑазÑÑÑÐµÐ½Ð¸Ñ Ð¿Ð¾Ð´ дейÑÑвием ÑÑаÑиÑеÑкиÑ
или динамиÑеÑкиÑ
нагÑÑзок. Ð
пÑоÑноÑÑи ÑÑдÑÑ Ð¿Ð¾ Ñ
аÑакÑеÑиÑÑикам меÑ
аниÑеÑкиÑ
ÑвойÑÑв, коÑоÑÑе полÑÑаÑÑ Ð¿Ñи
меÑ
аниÑеÑкиÑ
иÑпÑÑаниÑÑ
. Ð ÑÑаÑиÑеÑким иÑпÑÑаниÑм на пÑоÑноÑÑÑ Ð¾ÑноÑÑÑÑÑ
ÑаÑÑÑжение, ÑжаÑие, изгиб, кÑÑÑение, вдавливание. РдинамиÑеÑким оÑноÑÑÑÑÑ
иÑпÑÑÐ°Ð½Ð¸Ñ Ð½Ð° ÑдаÑнÑÑ Ð²ÑзкоÑÑÑ, вÑноÑливоÑÑÑ Ð¸ изноÑоÑÑойкоÑÑÑ. ÐлаÑÑиÑноÑÑÑÑ
назÑваеÑÑÑ ÑпоÑобноÑÑÑ Ð¼Ð°ÑеÑиалов ÑпÑÑго деÑоÑмиÑоваÑÑÑÑ, а плаÑÑиÑноÑÑÑÑ â
ÑпоÑобноÑÑÑ Ð¿Ð»Ð°ÑÑиÑеÑки деÑоÑмиÑоваÑÑÑÑ Ð±ÐµÐ· ÑазÑÑÑениÑ.
ÐÑзкоÑÑÑ â ÑÑо ÑвойÑÑво маÑеÑиала, коÑоÑое опÑеделÑÐµÑ ÐµÐ³Ð¾
ÑпоÑобноÑÑÑ Ðº поглоÑÐµÐ½Ð¸Ñ Ð¼ÐµÑ
аниÑеÑкой ÑнеÑгии пÑи поÑÑепенном ÑвелиÑении
плаÑÑиÑеÑкой деÑоÑмаÑии вплоÑÑ Ð´Ð¾ ÑазÑÑÑÐµÐ½Ð¸Ñ Ð¼Ð°ÑеÑиала. ÐаÑеÑÐ¸Ð°Ð»Ñ Ð´Ð¾Ð»Ð¶Ð½Ñ Ð±ÑÑÑ
одновÑеменно пÑоÑнÑми и плаÑÑиÑнÑми.
ТвеÑдоÑÑÑ â ÑÑо ÑпоÑобноÑÑÑ Ð¼Ð°ÑеÑиала ÑопÑоÑивлÑÑÑÑÑ
пÑÐ¾Ð½Ð¸ÐºÐ½Ð¾Ð²ÐµÐ½Ð¸Ñ Ð² него дÑÑгиÑ
Ñел.
ÐÑноÑливоÑÑÑ â ÑÑо ÑпоÑобноÑÑÑ Ð¼Ð°ÑеÑиала вÑдеÑживаÑÑ, не
ÑазÑÑÑаÑÑÑ, болÑÑое ÑиÑло повÑоÑно-пеÑеменнÑÑ
нагÑÑзок.
ÐзноÑоÑÑойкоÑÑÑ â ÑÑо ÑпоÑобноÑÑÑ Ð¼Ð°ÑеÑиала ÑопÑоÑивлÑÑÑÑÑ
повеÑÑ
ноÑÑÐ½Ð¾Ð¼Ñ ÑазÑÑÑÐµÐ½Ð¸Ñ Ð¿Ð¾Ð´ дейÑÑвием внеÑнего ÑÑениÑ.
ÐолзÑÑеÑÑÑ â ÑÑо ÑпоÑобноÑÑÑ Ð¼Ð°ÑеÑиала медленно и непÑеÑÑвно
плаÑÑиÑеÑки деÑоÑмиÑоваÑÑÑÑ (ползÑи) пÑи поÑÑоÑнном напÑÑжении (оÑобенно пÑи
вÑÑокиÑ
ÑемпеÑаÑÑÑаÑ
).
Ðоведение некоÑоÑÑÑ
меÑаллов (напÑимеÑ, оÑожженной ÑÑали) пÑи иÑпÑÑании на
ÑаÑÑÑжение показано на ÑиÑ. 3. ÐÑи ÑвелиÑении нагÑÑзки в меÑалле ÑнаÑала
ÑазвиваÑÑÑÑ Ð¿ÑоÑеÑÑÑ ÑпÑÑгой деÑоÑмаÑии, Ñдлинение обÑазÑа пÑи ÑÑом
незнаÑиÑелÑно. ÐаÑем наблÑдаеÑÑÑ Ð¿Ð»Ð°ÑÑиÑеÑкое ÑеÑение меÑалла без повÑÑениÑ
напÑÑжениÑ, ÑÑÐ¾Ñ Ð¿ÐµÑиод назÑваеÑÑÑ ÑекÑÑеÑÑÑÑ. ÐапÑÑжение, пÑи коÑоÑом
пÑодолжаеÑÑÑ Ð´ÐµÑоÑмаÑÐ¸Ñ Ð¾Ð±ÑазÑа без замеÑного ÑвелиÑÐµÐ½Ð¸Ñ Ð½Ð°Ð³ÑÑзки, назÑваÑÑ
пÑеделом ÑекÑÑеÑÑи. ÐÑи далÑнейÑем повÑÑении нагÑÑзки пÑоиÑÑ
Ð¾Ð´Ð¸Ñ ÑазвиÑие в
меÑалле пÑоÑеÑÑов наклепа (ÑпÑоÑÐ½ÐµÐ½Ð¸Ñ Ð¿Ð¾Ð´ нагÑÑзкой). ÐаиболÑÑее напÑÑжение,
пÑедÑеÑÑвÑÑÑее ÑазÑÑÑÐµÐ½Ð¸Ñ Ð¾Ð±ÑазÑа, назÑваÑÑ Ð¿Ñеделом пÑоÑноÑÑи пÑи
ÑаÑÑÑжении.
РиÑ. 3. ÐиагÑамма деÑоÑмаÑии пÑи иÑпÑÑании меÑаллов на
ÑаÑÑÑжение.
ÐапÑÑженное ÑоÑÑоÑние â ÑÑо ÑоÑÑоÑние Ñела, наÑ
одÑÑегоÑÑ Ð¿Ð¾Ð´
дейÑÑвием ÑÑавновеÑеннÑÑ
Ñил, пÑи ÑÑÑановивÑемÑÑ ÑпÑÑгом ÑавновеÑии вÑеÑ
его
ÑаÑÑиÑ. ÐÑÑаÑоÑнÑе напÑÑÐ¶ÐµÐ½Ð¸Ñ â ÑÑо напÑÑжениÑ, оÑÑаÑÑиеÑÑ Ð² Ñеле, поÑле
пÑекÑаÑÐµÐ½Ð¸Ñ Ð´ÐµÐ¹ÑÑÐ²Ð¸Ñ Ð²Ð½ÐµÑниÑ
Ñил, или возникаÑÑие пÑи бÑÑÑÑом нагÑевании и
оÑ
лаждении, еÑли линейное ÑаÑÑиÑение или ÑÑадка Ñлоев меÑалла и ÑаÑÑей Ñела
пÑоиÑÑ
Ð¾Ð´Ð¸Ñ Ð½ÐµÑавномеÑно.
ÐнÑÑÑенние напÑÑÐ¶ÐµÐ½Ð¸Ñ Ð¾Ð±ÑазÑÑÑÑÑ Ð¿Ñи бÑÑÑÑом оÑ
лаждении или нагÑевании в
ÑемпеÑаÑÑÑнÑÑ
зонаÑ
пеÑеÑ
ода Ð¾Ñ Ð¿Ð»Ð°ÑÑиÑеÑкого к ÑпÑÑÐ³Ð¾Ð¼Ñ ÑоÑÑоÑÐ½Ð¸Ñ Ð¼ÐµÑалла. ÐÑи
ÑемпеÑаÑÑÑÑ Ð´Ð»Ñ ÑÑали ÑооÑвеÑÑÑвÑÑ 400â600°. ÐÑли обÑазÑÑÑиеÑÑ Ð²Ð½ÑÑÑенние
напÑÑÐ¶ÐµÐ½Ð¸Ñ Ð¿ÑевÑÑаÑÑ Ð¿Ñедел пÑоÑноÑÑи, Ñо в деÑалÑÑ
обÑазÑÑÑÑÑ ÑÑеÑинÑ, еÑли они
пÑевÑÑаÑÑ Ð¿Ñедел ÑпÑÑгоÑÑи, Ñо пÑоиÑÑ
Ð¾Ð´Ð¸Ñ ÐºÐ¾Ñобление деÑали.
ÐÑедел пÑоÑноÑÑи пÑи ÑаÑÑÑжении в кг/мм2 опÑеделÑеÑÑÑ Ð½Ð°
ÑазÑÑвной маÑине как оÑноÑение нагÑÑзки Рв кÐ, необÑ
одимой Ð´Ð»Ñ ÑазÑÑÑениÑ
ÑÑандаÑÑного обÑазÑа (ÑиÑ. 4, а), к плоÑади попеÑеÑного ÑеÑÐµÐ½Ð¸Ñ Ð¾Ð±ÑазÑа в
мм2.
РиÑ. 4. ÐеÑÐ¾Ð´Ñ Ð¸ÑпÑÑÐ°Ð½Ð¸Ñ Ð¿ÑоÑноÑÑи маÑеÑиалов: а — на ÑаÑÑÑжение; б — на
изгиб; в — на ÑдаÑнÑÑ Ð²ÑзкоÑÑÑ; г — на ÑвÑÑдоÑÑÑ
ÐÑедел пÑоÑноÑÑи пÑи изгибе в кÐ/мм2 опÑеделÑеÑÑÑ ÑазÑÑÑением
обÑазÑа, коÑоÑÑй ÑÑÑанавливаеÑе» на двÑÑ
опоÑаÑ
(ÑиÑ. 4, б), нагÑÑженного
по ÑеÑедине ÑоÑÑедоÑоÑенной нагÑÑзкой Ð .
ÐÐ»Ñ ÑÑÑÐ°Ð½Ð¾Ð²Ð»ÐµÐ½Ð¸Ñ Ð¿Ð»Ð°ÑÑиÑноÑÑи маÑеÑиала опÑеделÑÑÑ Ð¾ÑноÑиÑелÑное Ñдлинение δ
пÑи ÑаÑÑÑжении или пÑогиб ƒ пÑи изгибе.
ÐÑноÑиÑелÑное Ñдлиненней δ в % опÑеделÑеÑÑÑ Ð½Ð° обÑазÑаÑ
,
иÑпÑÑÑемÑÑ
на ÑаÑÑÑжение. Ðа обÑÐ°Ð·ÐµÑ Ð½Ð°Ð½Ð¾ÑÑÑ Ð´ÐµÐ»ÐµÐ½Ð¸Ñ (ÑиÑ. 4, а) и измеÑÑÑÑ
Ð¼ÐµÐ¶Ð´Ñ Ð½Ð¸Ð¼Ð¸ ÑаÑÑÑоÑние до иÑпÑÑÐ°Ð½Ð¸Ñ (l0) и поÑле ÑазÑÑÑÐµÐ½Ð¸Ñ (l) и опÑеделÑÑÑ
Ñдлинение
δ = l-lo / lo · 100%
ÐÑогиб пÑи изгибе в мм опÑеделÑеÑÑÑ Ð¿Ñи помоÑи пÑогибомеÑа маÑинÑ,
ÑказÑваÑÑего пÑогиб ƒ, обÑазÑÑÑийÑÑ Ð½Ð° обÑазÑе в Ð¼Ð¾Ð¼ÐµÐ½Ñ ÐµÐ³Ð¾ ÑазÑÑÑÐµÐ½Ð¸Ñ (ÑиÑ. 4,
б).
УдаÑÐ½Ð°Ñ Ð²ÑзкоÑÑÑ Ð² кÐм/Ñм2 опÑеделÑеÑÑÑ Ð½Ð° обÑазÑаÑ
(ÑиÑ. 4, в), подвеÑгаемÑÑ
на копÑе ÑазÑÑÑÐµÐ½Ð¸Ñ ÑдаÑом оÑведенного в
ÑÑоÑÐ¾Ð½Ñ Ð¼Ð°ÑÑника. ÐÐ»Ñ ÑÑого ÑабоÑÑ Ð´ÐµÑоÑмаÑии в кÐм делÑÑ Ð½Ð° плоÑÐ°Ð´Ñ Ð¿Ð¾Ð¿ÐµÑеÑного
ÑеÑÐµÐ½Ð¸Ñ Ð¾Ð±ÑазÑа в Ñм 2.
ТвеÑдоÑÑÑ Ð¿Ð¾ ÐÑÐ¸Ð½ÐµÐ»Ñ (ÐÐ) опÑеделÑÑÑ Ð½Ð° заÑиÑенной повеÑÑ
ноÑÑи
обÑазÑа, в коÑоÑÑÑ Ð²Ð´Ð°Ð²Ð»Ð¸Ð²Ð°ÑÑ ÑÑалÑной ÑаÑик (ÑиÑ. 4, г) диамеÑÑом 5 или
10 мм под ÑооÑвеÑÑÑвÑÑÑей нагÑÑзкой в 750 или 3000 кРи замеÑÑÑÑ Ð´Ð¸Ð°Ð¼ÐµÑÑ d
обÑазовавÑейÑÑ Ð»Ñнки. ÐÑноÑение нагÑÑзки в кРк плоÑади лÑнки πd2 / 4 в
мм2 Ð´Ð°ÐµÑ ÑиÑло ÑвеÑдоÑÑи.
ÐоказаÑели Ð´Ð»Ñ Ð¼ÐµÑ
аниÑеÑкиÑ
ÑвойÑÑв Ð´Ð»Ñ Ð¾ÑновнÑÑ
Ñплавов пÑÐ¸Ð²ÐµÐ´ÐµÐ½Ñ Ð² Ñабл.
1.
ТаблиÑа.1. ÐеÑ
аниÑеÑкие ÑвойÑÑва оÑновнÑÑ
пÑомÑÑленнÑÑ
Ñплавов
Ð¢ÐµÑ Ð½Ð¸ÑеÑкое железо | 23 | 30 | 90 | ÐембÑÐ°Ð½Ñ |
ЧÑгÑн ÑеÑÑй | 12â38 | до 0,25 | 143â220 | ÐÑливки ÑаÑоннÑе |
ЧÑгÑн вÑÑокопÑоÑнÑй | 30â60 | 0,5â10 | 170â262 | ÐÑвеÑÑÑвеннÑе оÑливки |
СÑÐ°Ð»Ñ Ð¼Ð°Ð»Ð¾ÑглеÑодиÑÑÐ°Ñ (мÑгкаÑ) | 32 â 70 | 11 â 28 | 100â130 | ÐоÑелÑное железо ÑÑÑбÑ, коÑÐ»Ñ |
СÑÐ°Ð»Ñ ÑÑеднеÑглеÑодиÑÑÐ°Ñ (ÑÑедней ÑвеÑдоÑÑи) | 50â70 | 12 â 16 | 170 â 200 | ÐÑи, ÑаÑÑнÑ, валÑ, ÑелÑÑÑ |
СÑÐ°Ð»Ñ ÑвеÑÐ´Ð°Ñ Ð¿Ð¾Ñле закалки и оÑпÑÑка | 110â140 | до 9 | 400â600 | ÐнÑÑÑÑÐ¼ÐµÐ½Ñ ÑдаÑнÑй и ÑежÑÑий |
ÐÑонза оловÑниÑÑÐ°Ñ | 15 â 25 | 3â10 | 70â80 | ÐеÑали, ÑабоÑаÑÑие на иÑÑиÑание и подвеÑженнÑе коÑÑозии |
ÐÑонза алÑÐ¼Ð¸Ð½Ð¸ÐµÐ²Ð°Ñ | 40â50 | 10 | 120 | То же |
ÐаÑÑÐ½Ñ Ð¾Ð´Ð½Ð¾ÑÐ°Ð·Ð½Ð°Ñ | 25 â 35 | 30-60 | 42â60 | ÐаÑÑонно-гилÑзовое пÑоизводÑÑво |
ÐаÑÑÐ½Ñ Ð´Ð²ÑÑ ÑÐ°Ð·Ð½Ð°Ñ | 35â45 | 30â40 | _ | ÐеÑали, изгоÑовленнÑе гоÑÑÑей ÑÑамповкой |
СилÑмин | 21â23 | 1 â 3 | 65â100 | ÐеÑали в авиаÑÑÑоении и авÑоÑÑÑоении |
Ð¡Ð¿Ð»Ð°Ð²Ñ Ð¼Ð°Ð³Ð½Ð¸Ñ | 24 â 32 | 10â16 | 60â70 | То же |
Источник
