Стержень равного сопротивления растяжения сжатия

Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
Стержень равного сопротивления. При расчете на прочность стержня постоянного сечения с учетом собственного веса во всех сечениях стержня, кроме опасного, напряжения оказываются ниже допускаемого, т. е. материал недогружен (см., например, рис. 136, в). Однако можно спроектировать стержень такого переменного сечения, у которого во всех поперечных сечениях напряжения будут одинаковыми и равными допускаемому. Такой стержень
[c.131]
Что такое стержень равного сопротивления растяжению (сжатию)
[c.45]
Стержень равного сопротивления. При расчете на прочность стержня постоянного сечения с учетом собственного веса во всех
[c.141]
Стержень равного сопротивления имеет переменную площадь сечения, подобранную так, что напряжения во всех сечениях одинаковы (рис. 2.26). Площадь сечения на расстоянии х от свободного конца
[c.56]
Из чисто гео.метрических соображений ясно, что при той же длине /, толщине Н и нагрузке Р такой стержень равного сопротивления имеет вдвое меньший объем и массу, чем стержень постоянного сечения.
[c.144]
В то же время прогиб консольного стержня постоянного сечения по формуле (5.29) был равен F/ /(3 / ). Следовательно, стержень равного сопротивления, ширина которого меняется по закону треугольника, не только вдвое легче стержня постоянного сечения, но и и.меет в полтора раза больший прогиб. Благодаря этим свойствам такие стержни используются в качестве упругих элементов — рессор. для защиты от толчков и вибрации.
[c.144]
Стержень равного сопротивления. Напряжения и каждом сечении постоянны и равны допускаемому стержень имеет наименьший вес. Площадь поперечного сечения на расстоянии j от свободного конца
[c.24]
Стержень равного сопротивления……………………………………………………………………………………….76
[c.6]
Стержень равного сопротивления
[c.76]
По расходу материала стержень равного сопротивления является наиболее экономичным, но его трудно изготовить. Поэтому он применяется только в уникальных сооружениях (маяки, телебашни и т.д.). Обычно вместо стержня равного сопротивления
[c.77]
| Рис. 33. Стержень равного сопротивления и ему подобные стержни | 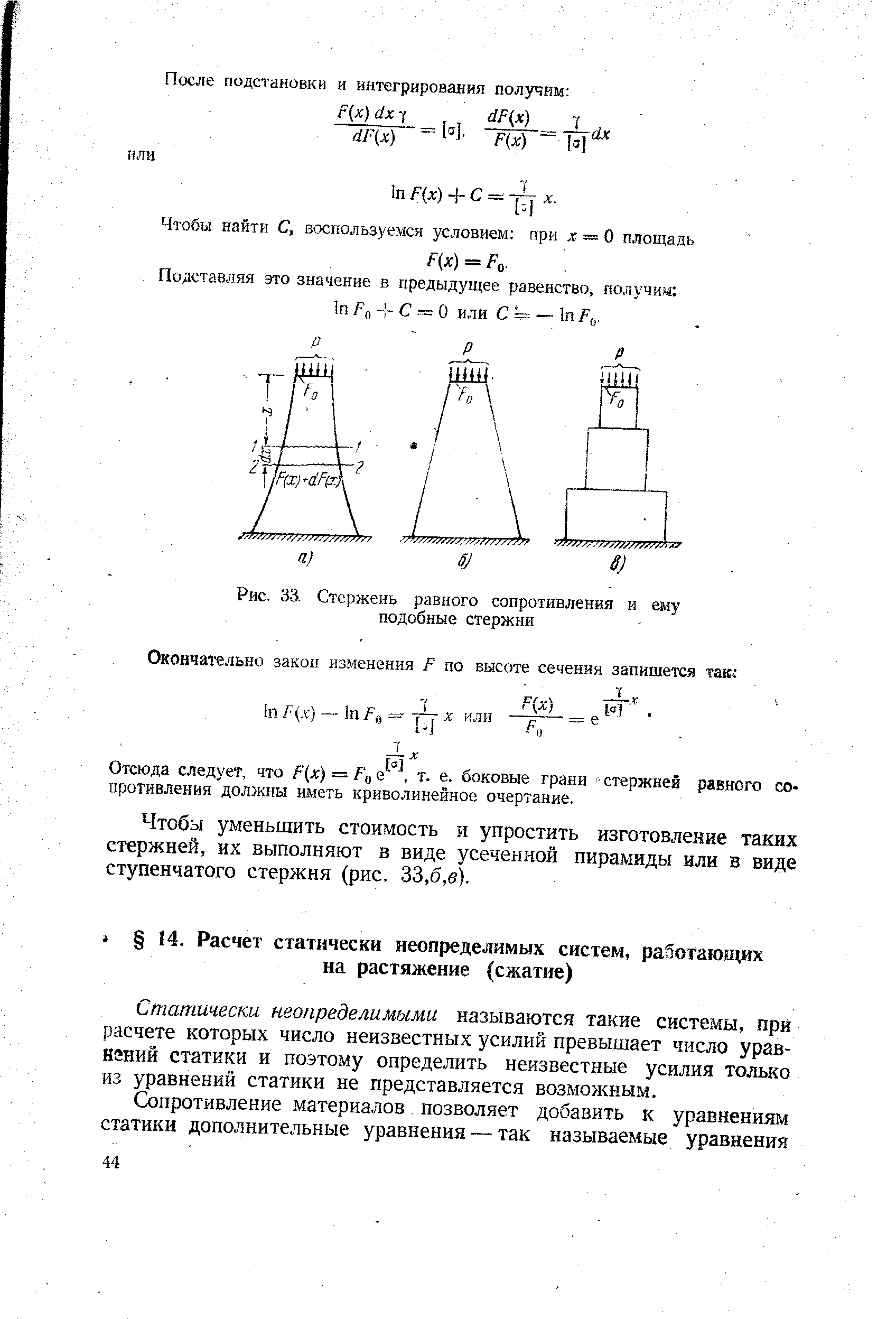 |
| Рис. 3.11. Стержень равного сопротивления | 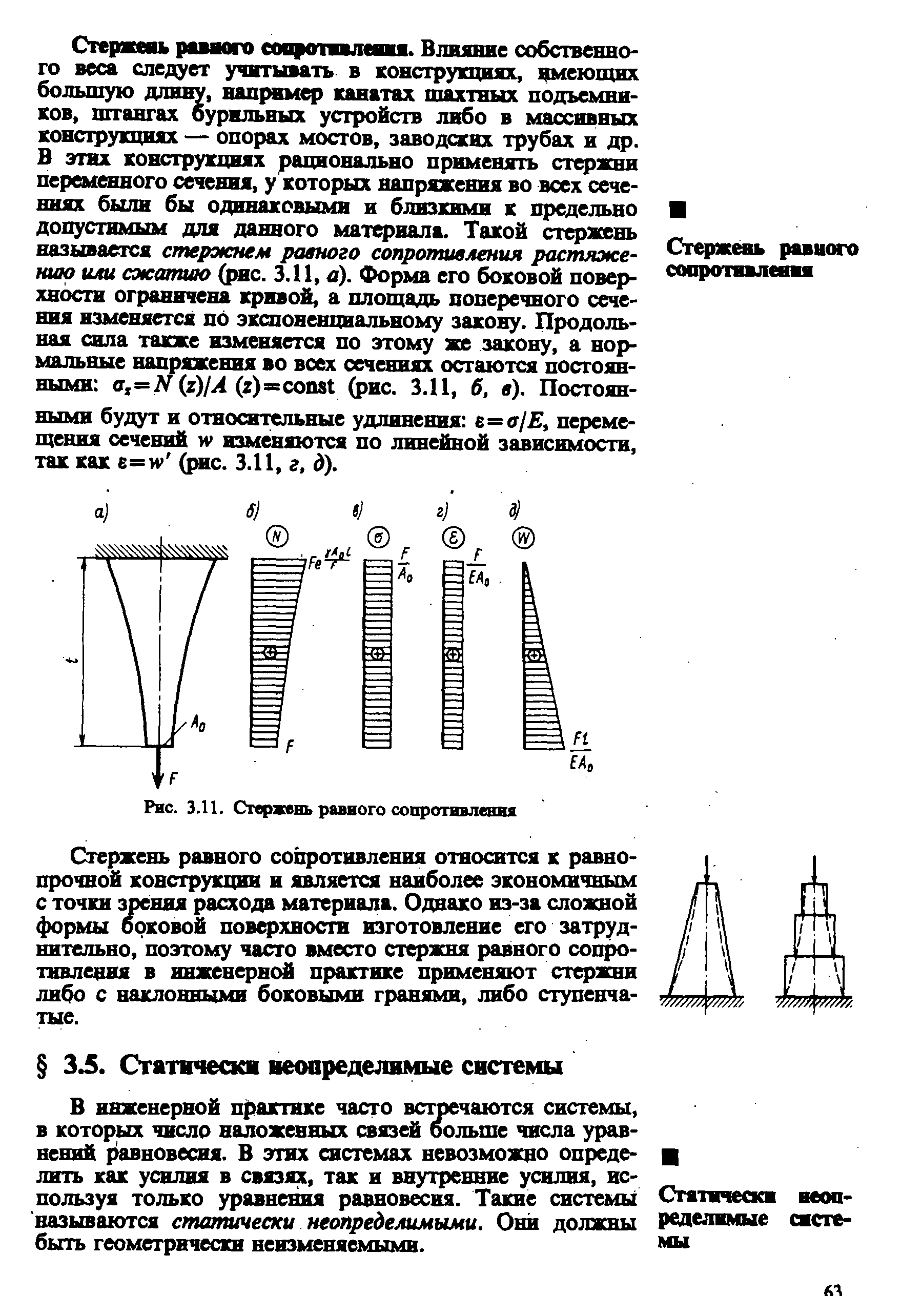 |
Ступенчатый стержень. Стержень, состоящий из отдельных участков (ступенек) с постоянной площадью поперечного сечения в пределах каждого участка, занимает промежуточное место между стержнем постоянного поперечного сечения и стержнем равного сопротивления. В ступенчатом стержне материал используется лучше,
[c.133]
Стержень, во всех поперечных сечениях которого напряжения одинаковы и равны допускаемому, называется стержнем равного сопротивления Это простейший пример равнопрочной конструкции, в которой материап используется наиболее эффективно.
[c.45]
Стержень (не-) круглого по.перечного сечения ( большой (малой) кривизны, равного сопротивления, прямолинейной формы…).
[c.86]
Ступенчатый стержень. Стержень, состоящий из отдельных участков (ступенек) с постоянной площадью поперечного сечения в пределах каждого участка, занимает промежуточное место между стержнем постоянного поперечного сечения и стержнем равного сопротивления. В ступенчатом стержне материал используется лучше, чем в стержне постоянного сечения, но менее эффективно, чем в стержне равного сопротивления. Последнее полностью окупается простотой изготовления ступенчатого стержня. Поэтому такие стержни имеют большее распространение, чем стержни равного сопротивления. В виде ступенчатых стержней иногда изготовляют опоры мостов.
[c.143]
СТЕРЖЕНЬ (БРУС) РАВНОГО СОПРОТИВЛЕНИЯ
[c.143]
Такой стержень называется стержнем равного сопротивления растяжению или сжатию. Если при этом напряжения равны допускаемым, то такой стержень будет иметь наименьший вес.
[c.85]
В случае длинных канатов или растянутых штанг. i форму стержня равного сопротивления осуществляют тоже приближенно, разделяя стержень по длине на Р ряд участков на протяжении каждого участка сечение
[c.86]
Запроектируем этот стержень как балку равного сопротивления с постоянной высотой /1оИ переменной шириной Ь х) по симметрии достаточно ограничиться рассмотрением одной половины пролета.
[c.306]
Стержнем равного сопротивления называется стержень переменного сечения, у которого напряжения во всех поперечных сечениях одинаковы и равны допускаемому (рис.5.15).
[c.76]
Подберем размеры колонны так, чтобы во всех ее сечениях рабочие напряжения имели постоянную величину, равную величине допускаемого напряжения. Такая колонна или такой стержень, называемый стержнем равного сопротивления, будет иметь минимальный вес. Расчеты, приводимые ниже, показывают, что этот стержень должен иметь криволинейное очертание боковых граней (рис. 33,а).
[c.43]
Какой стержень называется стержнем равного сопротивления
[c.54]
Если поперечное сечение определяется таким образом, что нормальные напряжения во всех сечениях будут одинаковы, то стержень получает форму тела равного сопротивления (фиг. 8).
[c.16]
Из полученных результатов видно, что для стального стержня длиной 40 м различие между призматическим брусом, ступенчатым брусом и брусом равного сопротивления весьма незначительно. Как видно из формулы (16), напряжение от собственного веса в призматическом стержне достигает 50% от [а] при длине стержня /Зз 0,05 [а]/у- Если стержень стальной, то, считая
[c.19]
Рессоры (рис. 11.1 ), упругие амортизаторы транспортных средств, состоят из нескольких (6…15) слабо изогнутых стержней прямоугольного сечения одинаковой ширины и разной длины такой, чтобы после сборки рессора была близка к балке равного сопротивления изгибу. До сборки у стержней (листов) кривизна различна она тем больше, чем короче стержень (рис. 11.12).
[c.372]
Уравнения (4.1) — (4.4)—это уравнения свободных колебаний стержня, при которых полная энергия, равная сумме потенциальной и кинетической, остается постоянной, так как эти уравнения не учитывают сил сопротивления. Если в уравнениях малых колебаний учесть силы вязкого сопротивления, пропорциональные вектору скорости (распределенные fa или сосредоточенные когда стержень имеет сосредоточенные массы)
[c.98]
Балка, подвергнутая воздействию трех сил, и та же балка, загруженная одной силой, представляющей собой равнодействующую указанных выше трех сил, изгибаются по-разному (рис. 1,9). Стержень, подвергнутый воздействию двух равных и противоположно направленных сил, в зависимости от того, где расположены точки их приложения, может быть весь растянут, растянутой может быть какая-либо его часть, и, наконец, может быть полное отсутствие растяжения. С точки зрения теоретической механики все три случая, изображенные на рис. 1.10, а, совершенно идентичны. При учете же деформируемости тела, осуществляемом в сопротивлении материалов, разница между тремя указанными случаями
[c.37]
Испытаниям подвергалась гидромуфта с поворотными черпа-ковыми трубками типовой конструкции ВНИИстройдормаша активным диаметром 420 мм. Для замера крутящих моментов на валах применялись фотоэлектрические датчики, не требующие токосъемных устройств и усиления сигналов. Датчик, замерявший усилия на черпаковых трубках, представлял собой стержень равного сопротивления, на который наклеены проволочные тензометры.
[c.64]
Стержень переменной ширины. При проектировании инженерных сооружений и механизмов стараются избегать неравномерного распределения напряжения по отдельным элементам. Такое неравномерное распределение ухудшает использование материала, так как малонапряженные части, увеличивая вес сооружения, слабо помогают напряженным частям нести внешнюю нагрузку. Прочность же всего сооружения определяется прочностью его наиболее напряженных частей. Конструкции, все элементы которых одинаково прочны, называют равнопрочными. Применительно к стержню, подвергающемуся изгибу, равнопрочность состоит в равенстве напряжений изгиба во всех его поперечных сечениях. Стержень, удовлетворяющий этому условию, называют стержнем равного сопротивления. Если заделанный одним концом и нагруженный поперечной силой на другом конце стержень имеет прямоугольное поперечное сечение, то сделать его равнопрочным можно, изменяя либо ширину либо высоту л сечения. Условие равнопрочности имеет вид
[c.143]
Мы говорили о колоссальных усилиях, до 75 тысяч тонн, развиваемых гидравлическими прессами. Однако уже сейчас нередки случаи, когда и этого недостаточно. Такая ситуация возникла, например, на одном заводе, на котором нужно было отштамповать крупную цилиндрическую заготовку. Специально для этого случая был предложен новый способ штамповки, так называемое термопрессование, позволяющее использовать колоссальные силы теплового расширения. Как известно из курса сопротивления материалов, сила, с которой стремится расшириться сжатый нагретый стержень, равна произведению модуля упругости материала на коэффициент его линейного расширения, на площадь поперечного сечения стержня и на разность температур до и после нагрева. Нагревая небольшой кубик из хромоникелевой стали (хромансиля) со стороной 10 сантиметров, можно через несколько секунд получить усилие в 1000 тонн. Причем для этого не требуется практически никакого оборудования.
[c.105]
Для оценки этого отклонения рассмотрим растянутый стержень, имеющий форму плоского треугольного клина (рнс. 222). Мы уже встречались со стержнем такой форхмы при решении задачи о балке равного сопротивления. Анализ показывает [3], что главные площадки расположатся по лучевым и концентрическим круговым сечениям (рис. 223). Поперечные сечения, нормальные к оси, не совпадают с главными, в них возникают касательные напряжения, и после деформации они перестают быть плоскими.
[c.225]
Индикатор со стержневой пружиной применяют при испытании машин, работающих до 2000 об/мин. В этом индикаторе (фиг. 27, б) вместо обычной спиральной пружины применена лружина 1 в виде конического стержня, имеющего очертание бруса равного сопротивления (на изгиб). Пружина эта ввинчивается таким образом, что шарик 3, которым оканчивается стержень, входит в предусмотренное для него отверстие в штоке поршня 2. Во время работы индикатора шарик 3, обладающий малой массой, совершает наибольшие перемещения. Это дает воз-56
[c.56]
Электродуговая С. При дуговой С. используется тепло вольтовой дуги, получаемой между углем и углем, между углем и металлом или между металлом и металлом. Обычно для С. применяют металлич. дугу, причем работают как постоянным, так и переменным током. Темп-ра вольтовой дуги 3 ООО—3 800° вольтова дуга постоянного тока развивает максимум тепла у положительного электрода, тогда как у отрицательного электрода на /-400° ниже, благодаря этому С. постоянным током обладает тем преимуществом, что к положительному полюсу можно присоединять более тугоплавкий из свариваемых предметов, например при С. предметов из стали с низким содержанием углерода более толстый предмет соединяют с положительным полюсом при сварке стали с большим содержанием углерода, наоборот, соединяют с положительным полюсом присадочный стержень. Наибольшее сопротивление имеет место в момент зажигания дуги при пуске тока напряжение зажигания для металлической дуги составляет ок. 65 V. Однако при самой С. напряжение снижается, и в зависимости от толщины электрода его целесообразно поддерживать в пределах 15—24 V. Для употребляемых в большинстве случаев электродов толщиной в 4 мм наиболее подходящим согласно данным практики является напряжение в 18 V. Так. обр. вольтова дуга имеет падающую характеристику, зависящую от длины дуги. Переход металла в вольтовой дуге происходит следующим путем жидкий металл стремится всегда от тонкого электрода присадочного прутка) к более массивному свариваемому предмету. Полагают, что металл притягивается последним вследствие перевеса в поверхностном напряжении. Магнитные силы при этом не могут йметь никакого влияния, так как раокаленное железо не обладает магнитными свойствами равным образом не влияет на переход материала и сила тяжести, в противном случае не представилось бы возможным производить потолочную С. Переход присадочного материала совершается большими или малыми каплями, что точно установлено новейшими изысканиями. Впервые это было выявлено из диаграммы силы тока и напрял ения процесса С., полученных при помощи осциллографа (фиг. 27). При этом было установлено, что сначала напряжение и сила тока немного колеблются, оставаясь в общем постоянными, что следует объяснить клокотанием капли на электроде, но затем напряжение внезапно падает, причем связанное с этим короткое замыкание свидетельствует о происшедшем в этот момент соединении между электродом и свариваемым предметом через посредство перенесенной капли. Эти выводы были подтверждены
[c.108]
Задача 1303 (рис. 707). Однородный стержень АВ длиной / и массой т, один конец которого закреплен при помощи шарнира, удерживается в вертикальном положении спиральной пружиной, жесткость которой равна q. На каждый элемент длины стержня ds при его вращении действует сила сопротивления, пропорциональная скорости этого элемента и его длине и направленная в сторону, противоположную скорости этого элемента, т. е. df = —fiuds. При вертикальном положении стержня пружина находится в ненапряженном состоянии. Принимая (5 = onst, определить, при каком значении жесткости j вертикальное положение стержня будет положением устойчивого равновесия. Найти также значение коэффициента Р, при котором стержень будет совершать малые затухающие колебания вблизи вертикального положения.
[c.465]
О А массы М= кг и длины / = 0,102 м шарнирно закреплен в точке О. Из верхнего вертикального своего положения стержень падает па недеформированный пружинный упор жесткости с = 2,7 кН/м, имея в начальный момент времени скорость точки А, равную 0(,= 1м/с. Пренебрегая массой пружигщого упора и неупругпми сопротивлениями движению, определить максимальную деформацию Vax пружины, если равновесным положени-
[c.131]
Однородный прямолинейный стержень ОА длины /=0,102 м, шарнирно закрепленный в точке О, начинает движение в вертикальной плоскости из крайнего верхнего своего положения, в котором начальная скорость точки А равна Uo=l м/с. Пренебрегая сопротивлениями, найти соотношение скоростей и v[c.132]
Сопротивление материалов 1986
(1986) — [
c.322
]
Сопротивление материалов Издание 13
(1962) — [
c.104
]
Источник
