Сопротивление материалов изгиб с растяжением
Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения.
Косой изгиб.
Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса.
В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.
Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Условие прочности при косом изгибе:
где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси.
Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности:
где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей.
Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям.
Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей:
Изгиб с растяжением (сжатием).
При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M.
Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса:
К расчёту на прочность бруса при изгибе с растяжением:
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид:
Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле:
где А — площадь поперечного сечения.
Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле:
Условие прочночти имеет вид:
Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям.
Внецентренное растяжение или сжатие.
При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.
К расчёту на прочность бруса при внецентренном растяжении
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Приведём силу F к центру тяжести:
где уF , xF — координаты точки приложения силы F.
В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле:
Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:
Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.
Кручение с изгибом.
Сочетание деформаций изгиба и кручения характерно для работы валов машин.
Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения:
Эпюры напряжений в сечении бруса при кручении с изгибом
Нормальное напряжение достигает максимума на поверхности:
Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала:
Из третьей и четвёртой теории прочности:
При кручении с изгибом условие прочности имеет вид:
Источник
В инженерной практике часто имеют место случаи одновременного действия на стержень поперечных и продольных нагрузок, причем последние могут быть приложены внецентренно. Такой случай показан на рис. 11.26. При этом внутренние усилия в заделке равны:
Рис. 11.26
Рис. 11.27
В общем случае растяжения или сжатия с изгибом внутренние усилия определяются раздельно от действия всех составляющих нагрузок. Нормальные напряжения в поперечных сечениях определяются по общей формуле
Приравняв это выражение нулю, получим уравнение нулевой линии
Положив в этом уравнении последовательно у = 0 и z = О, получим формулы для определения отрезков, отсекаемых нулевой линией на осях координат:
Как и во всех рассмотренных выше случаях сложного сопротивления, наибольшие растягивающие и сжимающие напряжения действуют в точках сечения, наиболее удаленных от нулевой линии. Для сечений типа прямоугольника и двутавра это противоположные угловые точки сечения. Значения наибольших и наименьших напряжений в угловых точках можно определить по формулам:
где величины изгибающих моментов Mz и Му надо взять по абсолютной величине.
Напомним, что во всех предыдущих решениях использовался принцип независимости действия сил, позволяющий определять внутренние усилия для недеформированного состояния стержня. Строго говоря, это возможно только при малых деформациях. В противном случае принцип независимости действия сил использовать нельзя.
Рассмотрим, например, консольный стержень в условиях сжатия с изгибом (рис. 11.27). Если стержень обладает значительной гибкостью и прогибы от поперечной нагрузки достаточно велики, то сила Р вызывает дополнительный изгиб, а изгибающий момент в заделке от ее действия равен М = PvB. Для негибких стержней этот момент незначителен и его можно не учитывать. Для гибких стержней необходимо проводить расчет по так называемой деформированной схеме с учетом влияния продольных сил на изгиб. Подобные задачи будут рассмотрены в гл. 13.
Пример 11.7. Для короткого консольного деревянного стержня круглого сечения, находящегося в условиях центрального сжатия и изгиба в плоскости Oxz (рис. 11.28), построим эпюру о в опасном сечении.
Рис. 11.28
Определяем геометрические характеристики сечения:
Строим эпюры внутренних усилий N и Му (рис. 11.28, а). Изгибающий момент Му вызывает растяжение волокон левой половины стержня и имеет наибольшее значение в заделке: Му = — 4 • 1,2 • 0,6 = —2,88 кНм. Изгибающий момент Mz равен нулю. Определяем значения наибольших нормальных напряжений в точках А и В в сечении вблизи заделки:
Напряжения во всех точках сечения стержня являются сжимающими. Эпюры о в опасном сечении от действия N и М и суммарная эпюра с приведены на рис. 11.28, б.
Пример 11.8. Для стального стержня, состоящего из двух неравнобоких уголков L 160x100x10, находящегося в условиях центрального растяжения и изгиба в плоскости Оху (рис. 11.29, а), определим расчетное значение силы Р из условия прочности и построим эпюру о в опасном сечении. Совместная работа уголков обеспечена соединениями, показанными пунктиром. В расчетах примем R= 210 МПа = 21 кН/см2, ус = 0,9.
Рис. 11.29
Определяем геометрические характеристики сечения:
Строим эпюры N w Mz (рис. 11.29, а). Опасным является сечение в середине стержня, где Mz имеет наибольшее значение. В нижних волокнах стержня нормальные напряжения от действия N и Mz имеют одинаковый знак и являются растягивающими. Из условия прочности по наибольшим растягивающим напряжениям в точке А
находим Р 29,4 кН. При действии силы Р = 29,4 кН напряжения в точках А и В равны:
Эпюры о в опасном сечении от действия N w Mzw суммарная эпюра а приведены на рис. 11.29, б.
Пример 11.9. Для стального консольного стержня составного сечения, находящегося в условиях внецентренного растяжения и изгиба (рис. 11.30, а), выполним проверку прочности и построим эпюру а в опасном сечении. В расчетах примем /? = 210 МПа, ус — 0,9.
Построим эпюры N, Mz, Му. Изгибающий момент Mz вызывает растяжение верхних волокон стержня и в заделке равен Mz = —10 • 3,6 — 15 • 1,8 = —63 кНм, а момент М вызывает растяжение волокон левой части сечения (при взгляде от положительного направления оси Ох) и имеет постоянное значение Му = —300 • 0,0625 = —18,75 кНм. Продольная сила является растягивающей и также имеет постоянное значение N = 300 кН.
Наибольшие нормальные напряжения действуют в сечении вблизи заделки (опасное сечение).
Рис. 11.30
Определяем геометрические характеристики сечения. Учитывая, что для двутавра 124 Fx = 34,8 см2, J = 3460 см4, Jy = = 198 см4, b = 11,5 см, И = 24 см, находим:
Наибольшие напряжения действуют в противоположных угловых точках опасного сечения. Определяем по формулам (11.17) отрезки, отсекаемые нулевой линией на осях координат. Учитывая, что в первой четверти сечения моменты Mz и Му вызывают сжатие и имеют отрицательный знак, находим:
Отложив у0 и Zq на осях координат, проводим нулевую линию. На прямой, перпендикулярной нулевой линии, строим эпюру о (рис. 11.30, б), которая является разнозначной. Наибольшие растягивающие напряжения возникают в точке Л . Напряжения в точках Л и В равны:
Поскольку оА = 123,7 МПа ycR = 189 МПа, прочность стержня обеспечена. Эпюра с в опасном сечении приведена на рис. 11.30, б.
Источник
Сложное сопротивление
имеет место в тех случаях, когда в
поперечных сечениях нагруженного
стержня одновременно действуют несколько
внутренних силовых факторов. В расчетах
используется принцип
суперпозиции
– принцип независимости действия сил,
согласно которому результат
действия группы сил на тело равен сумме
результатов действия каждой силы в
отдельности и не зависит от последовательности
нагружения.
Таким образом, определяют значения
напряжений от каждого силового фактора
отдельно, устанавливают наиболее
нагруженные сечения и точки, которые
проверяют по условиям прочности.
При
этом напряжения одного вида (только
нормальные или только касательные)
суммируются алгебраически. Напряжения
разного вида (нормальные и касательные)
приводят к одному виду – нормальным
напряжениям, эквивалентным по своему
воздействию.
Рассмотрим
некоторые из этих случаев.
П
Рис. 4.9
оперечный изгиб(рис. 4.9). Под
действием силыFв поперечных
сечениях стержня возникают одновременно
поперечная сила
и изгибающий момент
,
а следовательно, касательныеи нормальныенапряжения.
П
рактикой установлено, что в большинстве
реальных случаев поперечного изгиба
влияние касательных напряжений на
прочность стержня незначительно по
сравнению с влиянием нормальных
напряжений и в расчетах не учитывается.
В связи с этим все расчетные зависимости,
полученные для случая чистого изгиба,
могут быть использованы и для случая
поперечного изгиба.
Например, наибольшее
значение напряжений рассчитывают по
зависимости
.
Изгиб с
растяжением (сжатием)(рис. 4.10).
Под действием силы F
в поперечных сечениях консольного
стержня возникают одновременно нормальная
сила
,
поперечная сила
и изгибающий момент
.
Рис.
4.10
Е
Рис.27
сли пренебречь действием касательных
напряжений от поперечных сил, то
напряжения в любой точке поперечного
сечения стержня будут нормальными, а
наибольшие напряжения для осесимметричных
сечений определяют по формуле
.
Значения нормальной
силы и изгибающих моментов рассчитывают
с учетом правила знаков.
Изгиб с кручением
(рис. 4.11). Такой вид сложного сопротивления
характерен для валов механизмов,
представляющих собой круглые стержни.
Р
Рис. 4.11
ассмотрим круглый стержень,
нагруженный поперечной силой
,
вращающим моментом
и изгибающим моментом
.
В любой точке поперечного сечения будут
действовать одновременно нормальныеи касательныенапряжения.
Максимальные
нормальные напряжения изгиба рассчитывают
по зависимости
.
Пренебрегая
действием касательных напряжений от
поперечных сил, максимальные значения
касательных напряжений от кручения
рассчитывают по зависимости
.
Эквивалентные
напряжения
рассчитывают по одной из теорий прочности:
или
.
Для круглых стержней
расчетная зависимость может быть
представлена в виде
,
где
– приведенный момент, действие которого
эквивалентно совместному действию
изгибающегоМ
и крутящего Т
моментов; d
– диаметр поперечного сечения.
4.4. Рациональная форма сечений
Рациональная форма
сечения обеспечивает прочность
конструкции при минимальной площади
сечения, а следовательно, минимальный
вес и расход материалов.
Рациональная форма
сечения определяется характером
распределения напряжений в поперечном
сечении при различных видах деформаций.
Так, при растяжении,
сжатии и сдвиге напряжения распределяются
по сечению равномерно, а их величина
пропорциональна площади сечения и не
зависит от формы сечения.
При кручении и
изгибе напряжения по сечению распределяются
неравномерно, а их величина изменяется
от нуля до максимума. В этих случаях
рациональной будет такая форма, при
которой материал располагается в
наиболее нагруженных участках сечения.
В связи с этим
металлургическими предприятиями
выпускается стандартный профильный
прокат: труба, двутавр, швеллер, уголок
(рис. 4.12).
При кручении
наиболее рациональным является кольцевое
сечение (рис. 4.12, а),
т.к. максимальные касательные напряжения
действуют в периферийной части сечения.
При изгибе идеальным
является сечение, состоящее из двух
узких прямоугольников, связанных между
собой.
Из стандартных
профилей наиболее близко к идеальному
является двутавровое сечение (рис. 4.12,
б).
Рис. 4.12
Следует отметить,
что кроме формы сечения большое значение
имеет его расположение по отношению к
силовой плоскости изгиба. Для вертикальной
силовой плоскости более рациональное
расположение имеют профили, изображенные
на рис. 4.12, б,
в,
г,
а для горизонтальной силовой плоскости
– на рис. 4.12, д,
е.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Изгиб с растяжением
(сжатием) относится к видам сложного
сопротивления первой группы. При этом
виде сложного сопротивления могут
возникнуть пять внутренних силовых
факторов: продольная сила
,
поперечные силы
и
и изгибающие моменты
и
.
Если пренебречь влиянием касательных
напряжений на прочность бруса, из пяти
внутренних силовых факторов остаются
три
.
Этот случай сложного сопротивления был
подробно рассмотрен в разделе 12.2
настоящего пособия. Поэтому все формулы
для нормальных напряжений и условия
прочности, полученные в разделе 12.2,
могут быть применены и к рассматриваемому
виду сложного сопротивления. Следует
отметить, что при возникновении сложного
изгиба со сжатием, брус должен обладать
большой жесткостью, т.е. не терять
устойчивость.
Рассмотрим частный
случай действия нагрузки, при котором
возникает изгиб с растяжением. Балка
консольного типа (Рис.12.15,а) с прямоугольным
поперечным сечением. Балка нагружена
наклонной силой
,
лежащей в вертикальной плоскости.
Разложим силу
не две составляющие: горизонтальную
составляющую
и вертикальную составляющую
.
От вертикальной составляющей силы
возникает изгибающий момент
(Рис.12.15,б),
от горизонтальной составляющей силы
продольная сила
(Рис12.15,в).
Изгибающий момент
.
Изгибающий момент
меняется
по линейному закону, достигая максимального
значения в заделке, в сечении А, продольная
сила положительная и постоянная по
величине на всей длине балки.
Нормальные
напряжения в произвольно выбранной
точке сечения для рассматриваемого
частного случая определим по формуле
(12.2) при
:
.
(12.25)
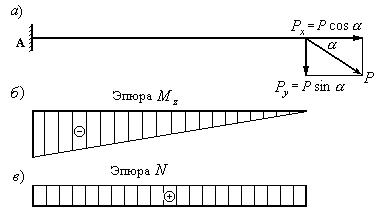
Рис.12.15
При определении
напряжений по формуле (12.25) применяем
принцип простого суммирования напряжений
от действия каждого из факторов в
отдельности. На рис.12.16 приведен
графический пример сложения напряжений.
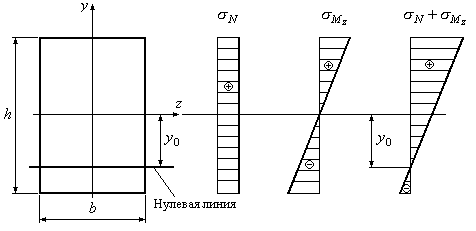
Рис.12.16
Уравнение нулевой
линии получим, приравняв нулю выражение
для напряжений:
,
(12.26)
откуда находим
ординату нулевой линии
.
Максимальные
напряжения действуют в волокнах, наиболее
удаленных от нулевой линии. Условие
прочности принимает вид:
.
(12.27)
Условие прочности
содержит две неизвестные величины –
оевой момент сопротивления
и площадь поперечного сечения
.
В большинстве случаев нормальные
напряжения от изгиба больше, чем от
растяжения или сжатия, поэтому при
подборе сечения можно вначале опустить
первое слагаемое и найти приближенное
значение для момента сопротивления.
Затем подбираются размеры поперечного
сечения по найденной величине момента
сопротивления. Размеры сечения берутся
несколько большими требуемых и далее
проверяется прочность выбранного
сечения по формуле (12.27).
12.6. Внецентренное растяжение (сжатие) прямого бруса
Внецентренное
растяжение (сжатие) относится к видам
сложного сопротивления первой группы.
Этот вид деформации вызывается действием
силы, параллельной продольной оси
стержня, но не проходящей через центр
тяжести поперечного сечения.
Рассмотрим брус
с произвольной формой поперечного
сечения, на который действует сила
,
параллельная оси бруса и пересекающая
любое поперечное сечение в точке А.
Координаты этой точки в системе главных
осей инерции сечения обозначим
и
(Рис.12.17). Расстояние точки А от центра
тяжести сечения обозначим буквой
назовем ексцентриситетом точки приложения
силы.
Приложим в точках
В и 0 две пары уравновешенных системы
сил. В результате получим две пары сил:
и
.
Кроме того, в точке 0 появится сила
,
действующая вдоль оси
.
Эти внешние силы вызовут в произвольном
прперечном сечении, лежащем на расстоянии
от основания фигуры, внутренние силовые
факторы:
;
;
.
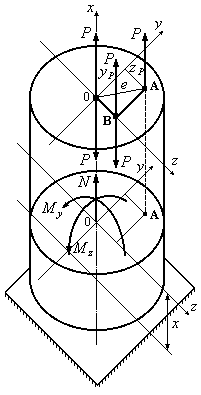
Рис.12.17
Таким образом,
напряжения в произвольной точке
поперечного сечения
будут складываться из напряжений,
вызванных продольной силой
и напряжениями чистого изгиба, вызванных
моментами
и
,
по формуле (12.2). После несложных
преобразований эту формулу можно
преобразовать к виду, выразив внутренние
усилия через внешнюю силу
:
.
(12.28)
Принимая во
внимание, что
;
квадраты радиусов
инерции сечения относительно главных
осей
и
,
формулу (12.28) преобразуем к виду:
.
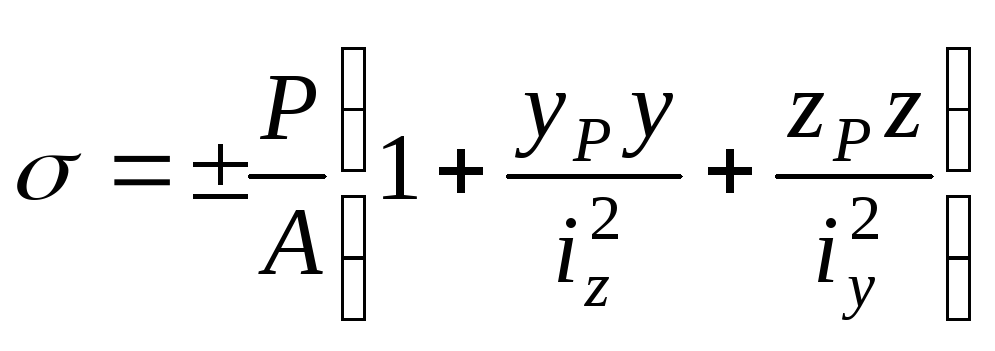(12.29)
При определении
напряжений по формуле (12.29) знак “+”принимается для случая, если сила
растягивающая. При сжимающей силе
перед скобкой в формуле (12.29) принимается
знак“”.
Поскольку при
внецентренном растяжении или сжатии
возникает осевое растяжение (сжатие) и
чистый пространственный изгиб, все
поперечные сечения стержня в одинаковой
степени опасны. Опасные же точки в
поперечном сечении найдем, построив
нулевую линию. Уравнение нулевой линии
получим, если приравняем нулю напряжения,
вычисленные по формуле (12.29) в произвольной
точке нулевой линии с координатами
и
:
.
(12.30)
Построим нулевую
линию (Рис.12.18).
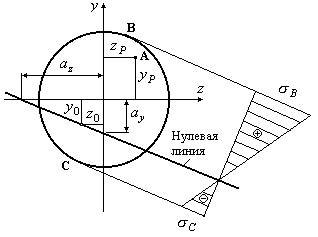
Рис.12.18
Так как координаты
нулевой линии
и
входят в формулу (12.30) в первой
степени, нулевая линия является прямой
линией. Следовательно, ее можно построить,
определив отрезки, которые нулевая
линия отсекает на осях координат
и
.
Для их определения зададим в формуле
(12.30) значение
.
Тогда, обозначив отрезок, который нулевая
линия будет отсекать на оси
через
и вводя его в формулу (2.30) вместо
,
получим:
.
(12.31)
Задавая
аналогичным образом из формулы (12.30)
получим:
.
(12.32)
Откладываем
найденные отрезки на осях координат
(Рис.12.18) и строим нулевую линию.
Проанализируем
поведение нулевой линии при внецентренном
растяжении (сжатии):
1. Нулевая линия –
прямая линия.
2. Нулевая линия
не проходит через центр тяжести
поперечного сечения.
3. Нулевая линия
проходит через две четверти координат,
ни одной из которых не принадлежит точка
приложения силы (нулевая линия никогда
не проходит через ту четверть, в
которой лежит точка приложения
силы).
Теперь, имея нулевую
линию, проводим параллельно ей касательные
к контуру сечения и находим наиболее
напряженные точки В и С в растянутой и
сжатой зонах сечения (Рис.12.18). Напряжения
в этих точках и условия прочности имеют
вид:
;
(12.33)
.
(12.34)
Координаты точек
приложения силы
и
, а также координаты А и В, в которых
определяются напряжения, проставляются
в формулах (12.33) и (12.34) со своими знаками.
Эпюра нормальных напряжений
для рассматриваемого случая внецентренного
растяжения приведена на рис.12.18.
Для прямоугольного
сечения максимальные напряжения лежат
в одной из угловых точек и условие
прочности удобно использовать в таком
виде:
.
(12.35)
Выше был рассмотрен
случай внецентренного растяжения.
Полученные формулы (12.33)-(12.35) справедливы
и для случая внецентренного сжатия при
условии, если нет опасности возникновения
продольного изгиба.
Рассмотрим несколько
примеров решения задач на внецентренное
растяжение и сжатие.
Пример 12.6. Стержень
прямоугольного профиля в точке А
подвергается действию растягивающей
силы силы
кН
(Рис.12.19). Определить наибольшие нормальные
напряжения в сечении стержня.
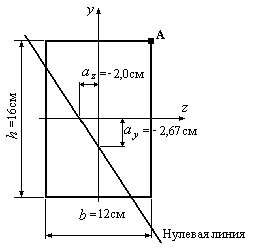
Рис.12.19
Решение:
1. Определяем
моменты инерции и квадраты радиусов
инерции сечения относительно главных
осей
и
:
см4;
см4;
см2;
см2.
2. Определяем
отрезки, определяемые нулевой линией
на осях координат:
см;
см.
3. Строим нулевую
линию (Рис.12.19).
4. Наиболее удаленной
от нулевой линии является точка А.
Напряжения в этой точке будут наибольшими:
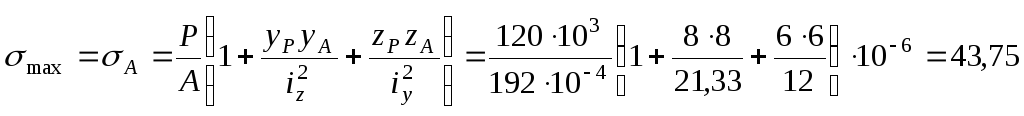МПа.
Пример 12.7.В
точках А двух коллонн приложены сжимающие
силы (Рис.12.20). При этом в точке С обеих
колонн сжимающие напряжения оказались
одинаковыми. Сравнить напряжения в
точках В обеих колонн.
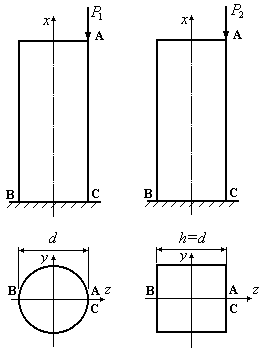
Рис.12.20
Решение:
1. Обозначим высоту
второй колонны буквой
и, учитывая, что для второй колонны
размер
,
вычислим для каждой колонны квадраты
радиусов инерции сечений относительно
оси
.
Для первой (левой)
колонны:
;
Для второй (правой)
колонны:
.
2. Определяем
напряжение в точке С для первой колонны:
.
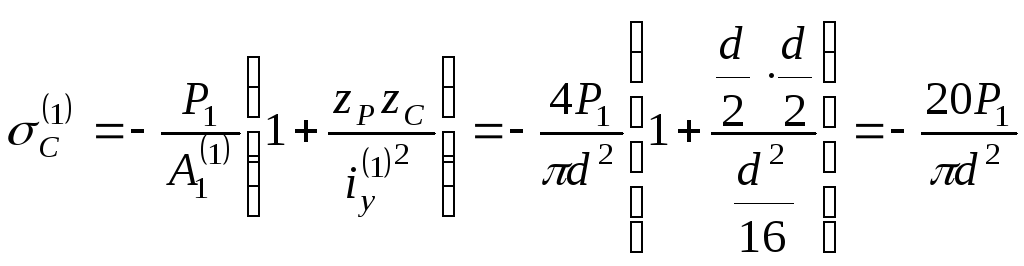(а)
3. Определяем
напряжение в точке С для второй колонны:
.
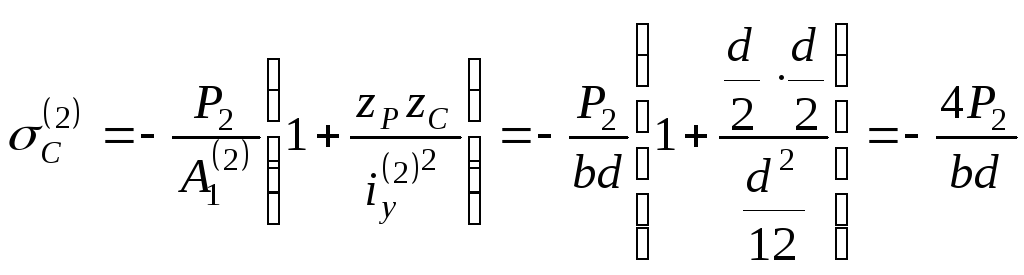(б)
4. По условию задачи
нормальные напряжения в точке С для
обеих колонн одинаковы, т.е.
.
Приравнивая выражения (а) и (б), выражаем
силу
через силу
:
.
(в)
5. Вычисляем
нормальные напряжения в точке В сечения
для первой колонны:
.
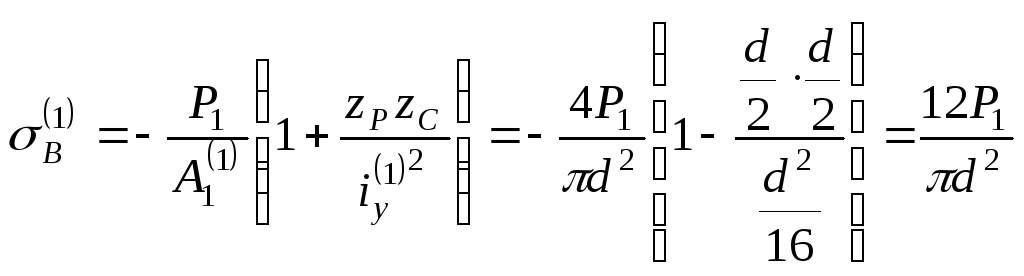(г)
5. Вычисляем
нормальные напряжения в точке В сечения
для второй колонны:
.
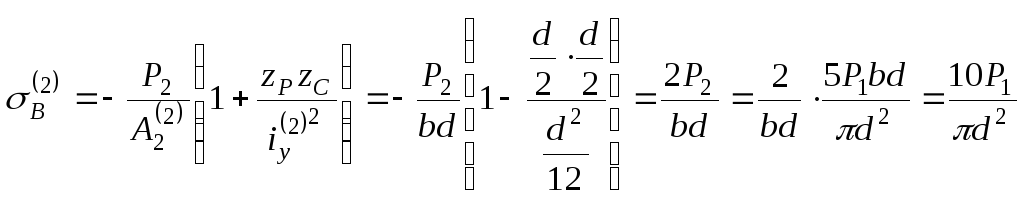(д)
6. Напряжение
.
Составим их отношение:
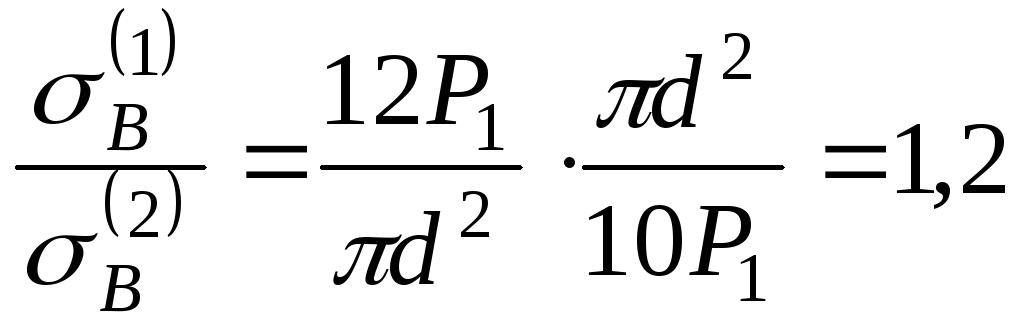
Таким образом,
напряжение в первой колонне на 20% выше,
чем во второй.
Пример 12.8.В
точках А и В колонны прямоугольного
сечения приложены одинаковые силы
(Рис.12.21а). Как изменится наибольшее
сжимающее напряжение в колонне, если
одну из сил удалить?
Решение:
1. Найдем напряжения
в колонне, когда действуют две симметрично
расположенные силы (Рис.12.21,б). Такое
приложение сил является центральным.
В этом случае нормальные напряжения от
сжатия найдем из формулы: