Сопромат сжатие растяжение курсовая
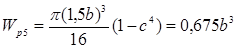
Расчет на прочность статически определимых систем при растяжении и сжатии. Последовательность решения поставленной задачи. Подбор размера поперечного сечения. Определение потенциальной энергии упругих деформаций. Расчет бруса на прочность и жесткость.
Подобные документы
Построение эпюры нормальных сил и напряжений. Методика расчета задач на прочность. Подбор поперечного сечения стержня. Определение напряжения в любой точке поперечного сечения при растяжении и сжатии. Определение удлинения стержня по формуле Гука.
методичка, добавлен 05.04.2010
Методическое указание по вопросам расчётов на прочность при различных нагрузках и видах деформации. Определение напряжения при растяжении (сжатии), определение деформации. Расчеты на прочность при изгибе, кручении. Расчетно-графические работы, задачи.
контрольная работа, добавлен 15.03.2010
Определение напряжений при растяжении–сжатии. Деформации при растяжении-сжатии и закон Гука. Напряженное состояние и закон парности касательных напряжений. Допускаемые напряжения, коэффициент запаса и расчеты на прочность при растяжении-сжатии.
контрольная работа, добавлен 11.10.2013
Условия статического равновесия. Закон распределения внутренних сил. Расчет распределенных и сосредоточенных нагрузок и момента. Площадь поперечного сечения нагруженных участков. Расчет на прочность узла конструкции при ускорении 5g по нормали к оси узла.
курсовая работа, добавлен 04.04.2015
Проведение расчета площади поперечного сечения стержней конструкции. Определение напряжений, вызванных неточностью изготовления. Расчет балок круглого и прямоугольного поперечного сечения, двойного швеллера. Кинематический анализ данной конструкции.
курсовая работа, добавлен 24.09.2014
Расчет статически определимой рамы. Перемещение системы в точках методом Мора-Верещагина. Эпюра изгибающих моментов. Подбор поперечного сечения стержня. Внецентренное растяжение. Расчет неопределенной плоской рамы и плоско-пространственного бруса.
курсовая работа, добавлен 04.12.2012
Определение и уточнение диаметра вала с целью оценки статической нагрузки на брус. Произведение расчета вала на прочность и жесткость при крутящем ударе и при вынужденных колебаниях. Выбор эффективных коэффициентов концентрации напряжений в сечении.
контрольная работа, добавлен 27.07.2010
Анализ прочности и жесткости несущей конструкции при растяжении (сжатии). Определение частота собственных колебаний печатного узла. Анализ статической, динамической прочности, а также жесткости печатного узла при изгибе, при воздействии вибрации и ударов.
курсовая работа, добавлен 11.12.2012
Определение равнодействующей плоской системы сил. Вычисление координат центра тяжести шасси блока. Расчёт на прочность элемента конструкции: построение эпюр продольных сил, прямоугольного и круглого поперечного сечения, абсолютного удлинения стержня.
курсовая работа, добавлен 05.11.2009
Гипотезы сопротивления материалов, схематизация сил. Эпюры внутренних силовых факторов, особенности. Три типа задач сопротивления материалов. Деформированное состояние в точке тела. Расчёт на прочность бруса с ломаной осью. Устойчивость сжатых стержней.
курс лекций, добавлен 04.05.2012
- главная
- рубрики
- по алфавиту
- вернуться в начало страницы
- вернуться к подобным работам
Источник
Задача № 1
Тема: Расчет на прочность статически определимых систем при растяжении и сжатии
Требуется:
1. Построить эпюру продольного усилия Ni
2. По условию прочности подобрать размер поперечного сечение «а», если ![]() =160 МПа
=160 МПа
3. Для рассчитанного размера поперечного сечения построить эпюру нормальных напряжений ![]()
4. Построить эпюру осевых перемещений W и найти наибольшую величину относительных деформаций ![]() , если
, если ![]()
5. Определить потенциальную энергию упругих деформаций U
 Дано: 7
Дано: 7
Р1
= 50 кН;
l
1
=
3 м
; Ø
a 2a
Р
2
=65 кН
; l2
=
2 м
; Ø2a a 2a
Р
3
=40 кН
; l3
=
3 м
; a
Р4
=10 кН;
l
4
=
1м
; D C B A
Формы сечения: Ra
P4
P3
P2
P1
А1
№ 11 А3
№ 4
А2
№ 9 А4
№ 7
IV III II I
l 1
l2
l3
l4
Ni
= ? ; ![]() = ? ;
= ? ; ![]() = ?; N1
= ?; N1
P1
![]() = ? ; “a
= ? ; “a
” = ? ; 45 55
15
+ Эп.N (kH)
—
16 50
3,69 2
+ Эп.σ(МПа)
—
13
1,99 2,986 3,534 6,9
Эп.∆l
(мм) +
Решение:
Определяется сила реакции опор RА из уравнения статики:
![]()

![]()
Делим на 4 участка, обозначая их римскими цифрами (I, II, III, IV), а также характерные сечения через заглавные буквы (А, В, С, D, Е).
Определяется продольная сила на каждом участке методом сечения:
![]()
![]()
![]()
![]()
![]()
Строится эпюра продольных сил Ni
Определяется площадь поперечных сечений на каждом участке
А1=а*а=а2
А2=2а*а=2а2
А3=2а*2а=4а2
![]()
Определяется нормальное напряжение на каждом участке через 1/а2
![]()
![]()
![]()
![]()
Определяется максимальное значение нормального напряжения, не превышающее допускаемого напряжения, равное 160 МПа: ![]()
Максимальное значение напряжения на третьем участке ![]()
Находится значение «а»:
![]()
Принимается а = 19,4мм
Определяются действительные значения площадей поперечных сечений:
![]()
![]()
![]()
![]()
Определяются истинные значения нормального напряжения на каждом участке:
![]()
![]()
![]()
![]()
10. Строится эпюра нормального напряжения ![]()
11. Определяется относительная продольная деформация на каждом участке:
![]() , где Е = 2 105МПа
, где Е = 2 105МПа
![]()
![]()
![]()
![]()
12. Определяется относительная продольная деформация ![]() по сечениям:
по сечениям:
![]()
![]()
![]()
![]()
![]()
13. Определяется относительное удлинение ![]() и строится эпюра этих значений (Рис 1д):
и строится эпюра этих значений (Рис 1д):
![]()
![]()
![]()
![]()
Определяется максимальное значение относительного удлинения: ![]()
14. Определяется удельная потенциальная энергия
![]()
![]()
![]()
![]()
![]()
![]()
15. Определяется полная удельная потенциальная энергия
![]()
![]()
![]()
16. Определяется относительная погрешность нормального напряжения:
![]()
![]()
Задача №2
Тема: Расчет на прочность статически неопределимых систем при сжатии и растяжении
Дано:
Схема бруса
Размеры и нагрузки
Материал брусьев – сталь 3
Допускаемое напряжение ![]()
Модуль продольной упругости ![]()
Требуется:
Определить допускаемую нагрузку для ступенчатого бруса
 Дано:
Дано:
l
= 30 см
= 0,3 м = 300 мм
А = 10 см2
=
![]()
К = 0,15
![]()
![]()
![]()
[Р] = ?
Эп.
N
(
kH
) Эп.
σ
(
kH
) Эп.
l
(мм)
Ra
+ — + — + —
A A
1.5l 3A
I 255 53
0,02
B 2A
II 133
В
l 0,047
C
C 425
С
1.5l 4P 4A
III 66,4 0,066
D
D
l
A
IV 255 159
E
0,035
E
∆
R
e
Решение:
Составляется уравнение статики
![]()
Составляется уравнение совместности деформации УСД:
![]() — от заданных сил
— от заданных сил
![]() — УСД (1)
— УСД (1)
![]()
Определяются продольные силы на каждом участке:
![]()
![]() =? когда нет RE
=? когда нет RE
Находим относительное удлинение на каждом участке
![]()
![]()
Определяется ![]() — относительное удлинение силы реакции опор, когда нет сил Р и 2Р:
— относительное удлинение силы реакции опор, когда нет сил Р и 2Р:
![]()
![]()
![]()
Подставляем значения ![]() и
и ![]() в уравнение (1)
в уравнение (1)
![]()
![]()
![]()
Подставляем значение силы ![]() в уравнение статики
в уравнение статики ![]()
Определяем значения продольных сил, подставляя значения ![]()
![]()
![]()
![]()
![]()
Определяется значение нормального напряжения на каждом участке ![]()
![]()
![]()
![]()
![]()
Находим максимальное значение нормально напряжения
![]()
Принимаем Р = 170 кН
Определяются действительные значения продольных сил:
![]()
![]()
![]()
10. Определяются истинные значения нормального напряжения на каждом участке ![]() :
:
![]()
![]()
![]()
![]()
Находим относительное удлинение ![]()
![]()
![]()
![]()
![]()
![]()
Находим относительное удлинение по сечениям ![]()
![]()
![]()
![]()
![]()
![]()
Определяем относительное удлинение ![]()
![]()
![]()
![]()
![]()
По заданной формуле вычисляем значение зазора ![]() , оно должно соответствовать значению
, оно должно соответствовать значению ![]()
![]()
Проверка
![]()
Задача № 3
Тема: Расчет на прочность статически неопределимых систем при растяжении и сжатии.
Требуется:
Найти усиление и напряжение в стержнях, выразив через силу Р1
Определить допускаемую нагрузку [Р], если [σ] = 160 МПа
Найти предельную нагрузку Рпр, если [σ1] = 240 МПа и h1 = 1,5
Сравнить величины допускаемых нагрузок Рпр и Р, для чего найти их отношения.
![]()

Дано:
А=14см2 = 14·10 — 4м
а=2,3м
![]() в=2,7см
в=2,7см
с=1,7см
[σ] =160 МПа
hТ = 1,5
![]()
Найти: Р=?, РТ =?, [РТ] =?
Решение.
1. Составляется уравнение статики для стержневой системы
1. Σ Мi = 0; Ν1·a-P(a+c) +N2cos 45·b =0
2. Σ Zi =0; Z0 +Ν2· cos45 = 0
3. Σ Yi =0; Y0 + Ν1– P — N2·cos 45 = 0
В три уравнения равновесия входят четыре неизвестные силы, и, следовательно, задача является статически неопределимой. Для составления уравнения рассмотрим деформацию конструкции.
2. Рассмотрим подобие двух треугольников ![]() ;
;
Рассмотрим ![]() для нахождения деформации системы.
для нахождения деформации системы.
OB=b OA=a
![]()
![]()
![]()
![]()
![]() y0
y0
N1![]() В
В
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() N2
N2
Р P ![]()
B1
∆l1
B2
O A
B A1
∆l2
![]()
![]()
3. Подставляем ![]()
![]() в уравнение моментов и выражаем их через Р
в уравнение моментов и выражаем их через Р
![]()
![]()
![]()
![]()
4. Находим значения нормальных напряжений σ1, σ2
σ1 = ![]()
σ1 = ![]()
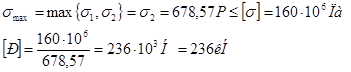
Принимаем ![]()
5. Находим действительные значения Ni
![]()
6. Находим действительные значения σi
σ1 = ![]() =678,57
=678,57![]()
![]() =160МПа
=160МПа
σ2 = ![]() =339,29
=339,29![]()
![]() =79,7МПа
=79,7МПа
7. Определяем предельную нагрузку Pпр, исходя из условия равновесия
Σ Мi = 0; Ν1·а– Р·(a+c) + N2cos 45·b =0, где N1 = σт · А, и N2 = σт · 2А; σт=240МПа

8. Находим предельно допускаемую нагрузку
![]()
![]()
Задача № 4
Тема: Расчет статически определимых брусьев на прочность и жесткость при кручении.
Дано:
Схема бруса.
Размеры нагрузки.
Требуется:
Рассчитать брус на прочность и жесткость
Построить эпюры крутящих моментов, касательных напряжений и углов поворота.

![]() Дано:
Дано:
m1 = 400 Н∙м
m2 = 1200 Н∙м
m3 = 2400 Н∙м
m4 = 400 Н∙м
m5 = m5 Н∙м
[τ] = 40 МПа
[θ] = 0,5 ![]()
d = 0,5
d1 = 1.5b
d2 = 2b
d3 = 2.5b
![]() a = 0.3 м
a = 0.3 м
Найти: Т, τ, θ — ?
Решение.
Составим уравнение статики:
Σ Мi = 0
m1 – m2 – m3 + m4 + m5 = 0
m5 = — m1 + m2 + m3 – m4 = — 400 + 1200 + 2400 – 400 = 2800 H·м
T1 = + m1 = 400 H·м
T2 = m1 – m2 = 400 – 1200 = — 800 H·м
T3 = m1 – m2 – m3 = — 800 – 2400 = — 3200 H·м
T4 = m1 – m2 – m3 = — 800 – 2400 = — 3200 H·м
T5 = m1 – m2 – m3 + m4 = – 2800 H·м
T6 = m1 – m2 – m3 + m4 + m5 = 0 H·м
Определяем полярный момент сопротивления на каждом участке Wpi:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определяется касательное напряжение на каждом участке по формуле  , выражая каждое значение через 1/b3
, выражая каждое значение через 1/b3
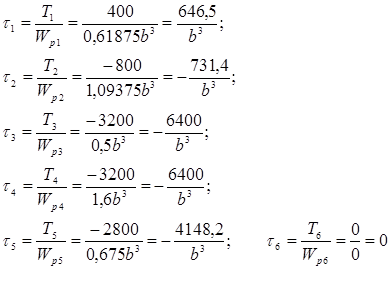
Определяем максимальное значение касательного напряжения из пяти значений:
τmax = max {τ1, τ2, τ3, τ4, τ5} ≤ [τ] ;
τ3 ≤ [τ]
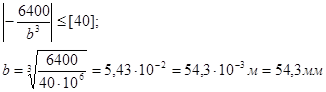
Определяется полярный момент инерции по данной формуле ![]() на каждом участке:
на каждом участке:
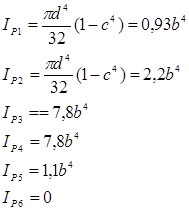
5. Определяем относительный угол закручивания по формуле
![]()
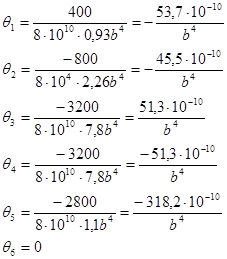
Определяем максимальное значение:
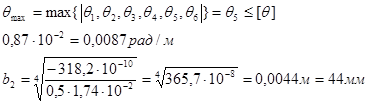
Примем максимальное значение из полученных значений b:
b≥{|b1|,|b2|} = b1 = 54,3 мм = 54,3·10 — 3 м = 55мм
6. Определяем действительные значения касательного напряжения τi:
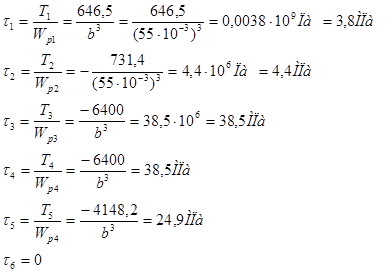
Определяем действительные значения относительного угла закручивания θi:
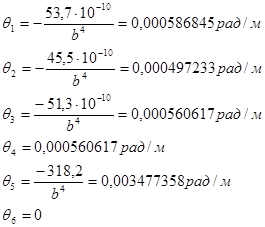
Определяем по формуле значение перемещения
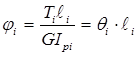
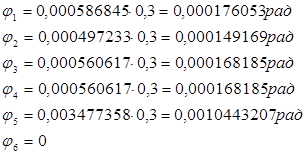
Находим числовые значения перемещения Δφi по сечениям:
φА = 0
φВ = φА + φ1 = 0 + 0,000176053 = 0,000176053 рад;
φС = φВ + φ2 = 0,000176053 + 0,000149169 = 0,000325222 рад;
φD = φС + φ3 = 0,000325222 + 0,000168185 = 0,000493407 рад;
φЕ = φD + φ4 = 0,000493407 + 0,000168185 = 0,000661592 рад;
φF = φЕ + φ5 = 0,000661592 + 0,003477358 = 0,00413895 рад;
φG = φF + φ6 = 0,00413895 + 0= 0,00413895 рад.
Источник
Оценка размеров поперечного сечения. Нахождение момента инерции относительно центральных осей. Расчет прочно-плотного заклепочного шва. Построение эпюр поперечных сил и изгибающих моментов. Проектный расчет вала при совместном действии кручения и изгиба.
Подобные документы
Выполнение проектировочного расчета на прочность и выбор рациональных форм поперечного сечения. Выбор размеров сечения балки при заданной схеме нагружения и материале. Определение моментов в характерных точках. Сравнительный расчет и выбор сечения балки.
презентация, добавлен 11.05.2010
Выбор материала, его характеристик и допускаемых напряжений. Расчет прочности и жесткости балок и рам, ступенчатого стержня и стержня постоянного сечения, статически неопределимой стержневой системы при растяжении-сжатии и при кручении. Построение эпюр.
курсовая работа, добавлен 06.12.2011
Свойства материалов при расчетах на прочность, жесткость и устойчивость определяются механическими характеристиками. Испытания над материалами проводят на деформацию растяжения, сжатия, кручения, изгиба при действии статической или переменной нагрузок.
реферат, добавлен 13.01.2009
Техническая характеристика стана ХПТ-55. Расчет станины рабочей клети. Моменты инерции сечений. Расчет валков на прочность и жесткость. Схема действия сил на рабочий валок и эпюры изгибающих и крутящих моментов. Расчет подушек валков, напряжение изгиба.
курсовая работа, добавлен 26.11.2012
Анализ напряженно-деформированного состояния стержня с учётом собственного веса при деформации растяжения, кручения и плоского поперечного изгиба. Определение касательных напряжений. Полный угол закручивания сечений. Прямоугольное поперечное сечение.
контрольная работа, добавлен 28.05.2014
Расчеты значения продольной силы и нормального напряжения для ступенчатого стального бруса. Центральные моменты инерции сечения. Построение эпюры поперечных сил и изгибающих моментов от расчетной нагрузки. Определение несущей способности деревянной балки.
контрольная работа, добавлен 01.02.2011
Решение задачи на нахождение параметров изгиба однопролетной балки со свободно опертым и упруго-защемленными концами. Определение значения изгибающих моментов, действующих на балку в любом сечении по её длине и экстремального значения изгибающего момента.
курсовая работа, добавлен 02.12.2009
Методика, содержание и порядок выполнения расчетно-графических работ. Расчеты на прочность при растяжении, кручении, изгибе. Расчет бруса на осевое растяжение. Определение размеров сечений балок. Расчет вала на совместное действие изгиба и кручения.
методичка, добавлен 24.11.2011
Построение расчетной схемы вала и эпюр внутренних силовых факторов. Расчет диаметра вала и его прогибов в местах установки колес; расчет на изгибную жесткость. Выбор типа соединения в опасном сечении вала. Расчет коэффициента запаса усталостной прочности.
дипломная работа, добавлен 26.01.2014
Выбор двигателя привода редуктора, определение номинальной мощности двигателя, передаточных чисел, силовых и кинематических параметров привода. Проектный расчет закрытой зубчатой передачи. Построение эпюр изгибающих и крутящих моментов на тихоходном валу.
курсовая работа, добавлен 22.04.2019
- главная
- рубрики
- по алфавиту
- вернуться в начало страницы
- вернуться к подобным работам
Источник
Ðàñ÷åò íà ïðî÷íîñòü ñòàòè÷åñêè îïðåäåëèìûõ ñèñòåì ïðè ðàñòÿæåíèè è ñæàòèè. Ïîñëåäîâàòåëüíîñòü ðåøåíèÿ ïîñòàâëåííîé çàäà÷è. Ïîäáîð ðàçìåðà ïîïåðå÷íîãî ñå÷åíèÿ. Îïðåäåëåíèå ïîòåíöèàëüíîé ýíåðãèè óïðóãèõ äåôîðìàöèé. Ðàñ÷åò áðóñà íà ïðî÷íîñòü è æåñòêîñòü.
Ñòóäåíòû, àñïèðàíòû, ìîëîäûå ó÷åíûå, èñïîëüçóþùèå áàçó çíàíèé â ñâîåé ó÷åáå è ðàáîòå, áóäóò âàì î÷åíü áëàãîäàðíû.
18
