Сопромат построение эпюр растяжения
Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки или рамы и | |
Операции
Узел С чего начать построение расчётной модели — видео
/ видео откроется в отдельной панели данного окна /Узлы — это основа для создания стержней и всей расчётной модели.
Введите
координаты узлаX,
м:Y, м: Стержень Для выполнения данной операции необходимо создать как минимум пару узлов. Для создания узлов используйте пункт меню
«Узел» в данной панели.С чего начать построение расчётной модели — видео
/ видео откроется в отдельной панели данного окна /Стержни создаются на основе узлов.
Закрепление одностепенное на узле
на стержнеДля выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте
пункт меню «Узел» в данной панели.Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней
используйте пункт меню «Стержень» в данной панели.Закрепление двухстепенное на узле
на стержнеДля выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте
пункт меню «Узел» в данной панели.Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней
используйте пункт меню «Стержень» в данной панели.Жёсткая заделка Для выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте
пункт меню «Узел» в данной панели.Сила на узле
на стержнеДля выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте
пункт меню «Узел» в данной панели.Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней
используйте пункт меню «Стержень» в данной панели.Момент на узле
на стержнеДля выполнения данной операции необходимо сначала создать один или несколько узлов. Для создания узлов используйте
пункт меню «Узел» в данной панели.Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней
используйте пункт меню «Стержень» в данной панели.Распределённая нагрузка Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней
используйте пункт меню «Стержень» в данной панели.Настройки Точность расчёта Количество знаков после запятой Эпюру изгибающего момента (Mx) строить на сжатом волокне растянутом волокне Эпюры строить в долях (qa) q, кН/м: a, м: Ширина иллюстраций в отчёте и графических окон в режиме просмотра результата, px:
/
Высота определится автоматически по содержимому. Рекомендуемое значение ширины — 300…350.
/
Объекты
В данном расчёте не задано ни одного объекта. Для создания объектов модели перейдите в раздел «Операции»
Источник
Расчет рамы/фермы
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
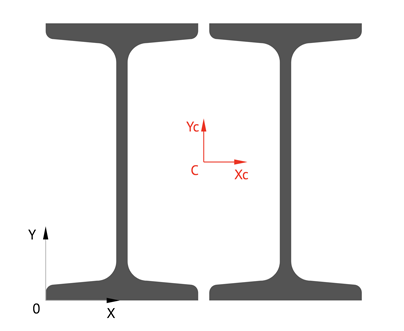
Расчет
геометрических характеристик поперечного сечения
Определение
центра тяжести, моментов инерции, моментов сопротивления
Формирование
подробного отчета

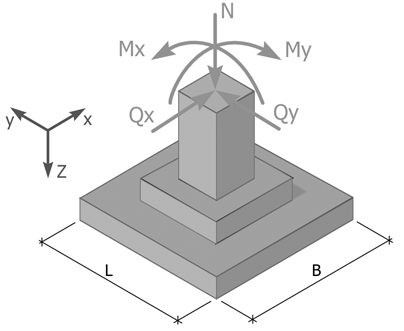
Расчет
столбчатого фундамента
Расчет
ленточного фундамента
Формирование
подробного отчета
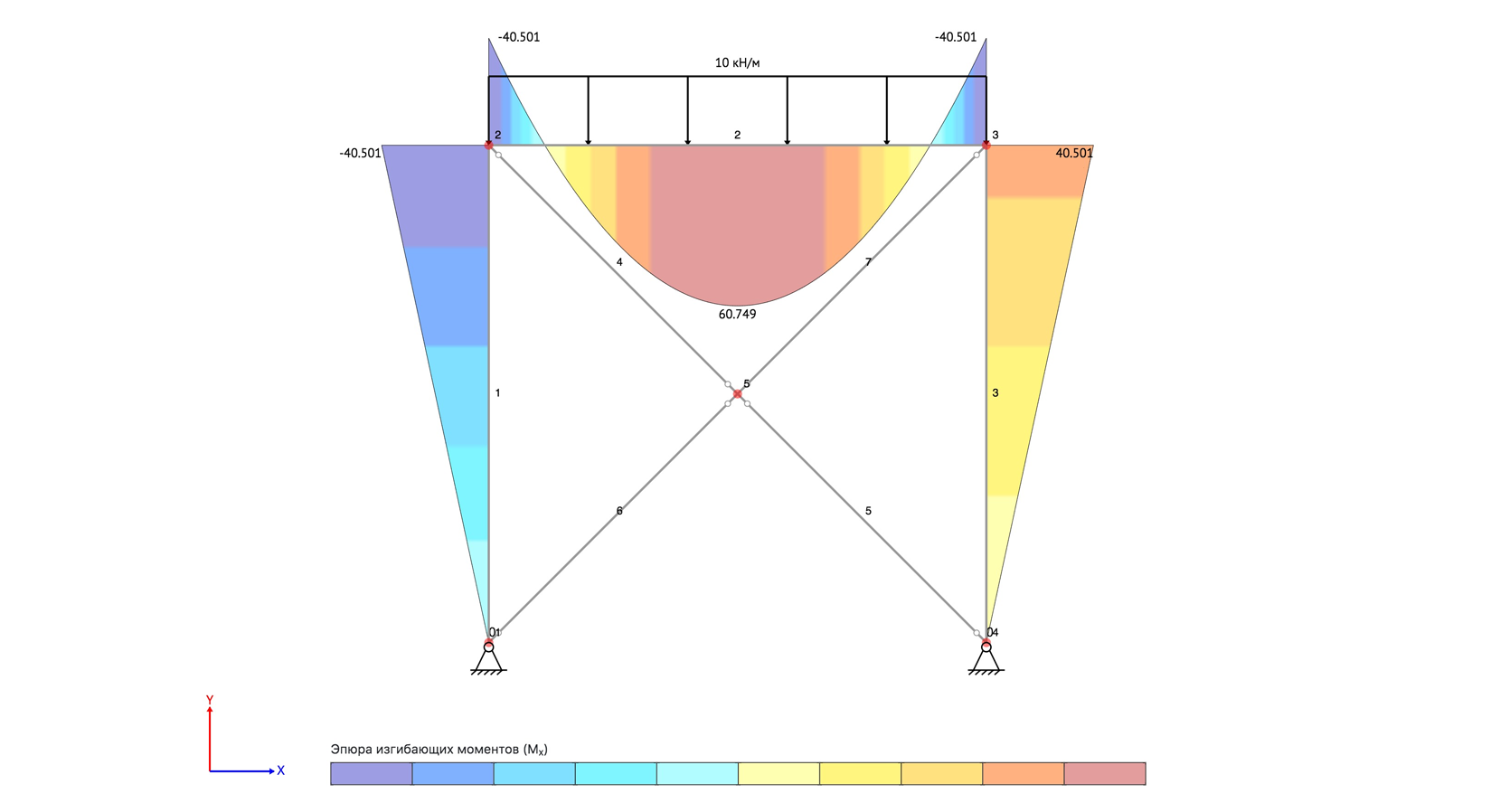
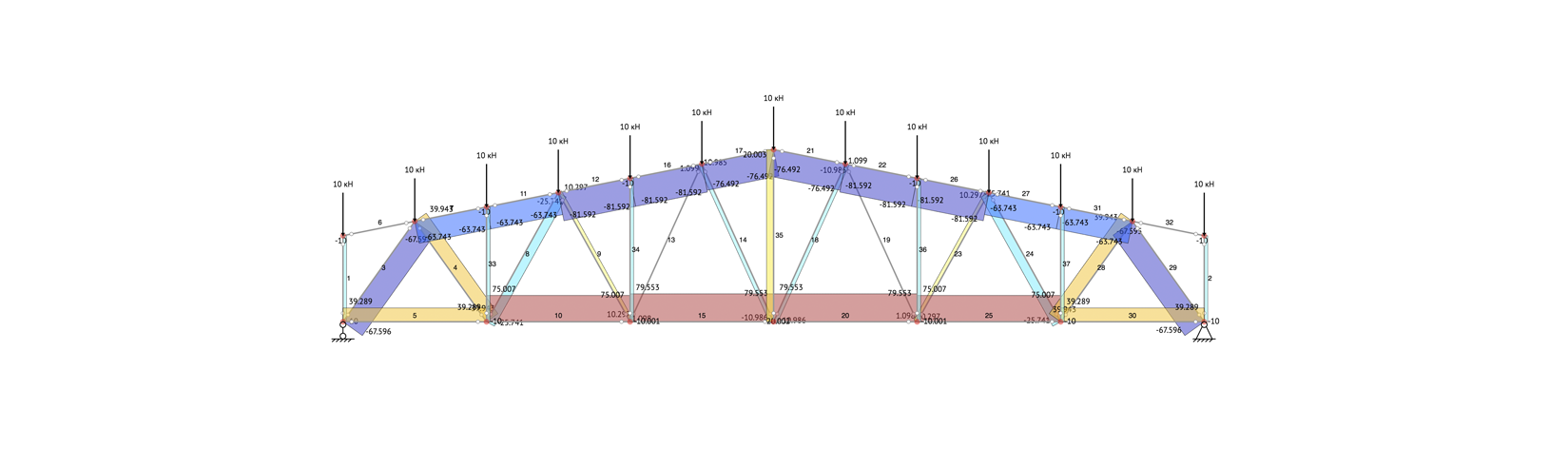
Расчет
статически-неопределимых систем
Расчет
методом конечных элементов
Построение
эпюры моментов (М)
Построение
эпюры поперечных сил (Q)
Построение
эпюры продольных сил (N)
Источник
Рассмотрим подробно порядок построения эпюр внутренних силовых факторов в раме.
Задача
Построить эпюры внутренних продольных и поперечных усилий и изгибающих моментов для плоской П-образной рамы, нагруженной силой, моментом и распределенной нагрузкой: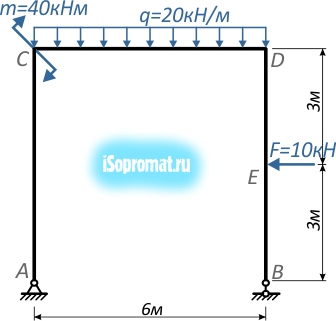
Рис. 1
Решение
Рама состоит из трех частей (левая и правая вертикальные стойки соединенные горизонтальным ригелем), но при этом имеет четыре силовых участка – AC, CD, BE и DE, на каждом из которых нам потребуется определить величину и направление внутренних усилий.
Для заданной расчетной схемы рамы ранее мы уже определили опорные реакции.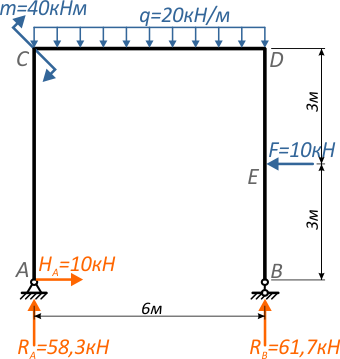
Рис. 2
Расчет значений
Обозначим силовые участки римскими цифрами.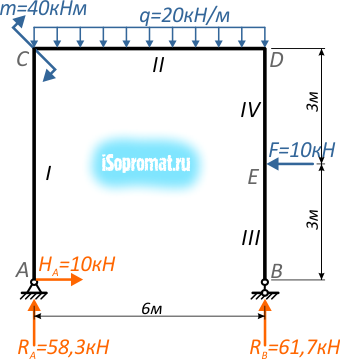
Рис. 3
Для расчета значений, необходимых для построения эпюр, будем пользоваться методом сечений и соответствующими правилами знаков.
Начинаем с первого силового участка AC.
Мысленно рассекаем его в любом месте между крайними точками участка.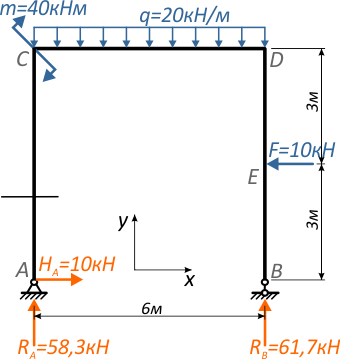
Рис. 4
Это сечение делит раму на две части:
- нижнюю часть стойки до точки A
- всю остальную часть, включая верхнюю от сечения часть левой стойки, ригель CD и правую стойку BD.
Наш видеоурок построения эпюр внутренних силовых факторов для балки:
Можно рассмотреть любую из них, но для упрощения расчетов рекомендуется выбирать менее нагруженную часть конструкции.
Очевидно, что в данном случае проще рассматривать нижнюю часть стойки.
Расстояние от границы участка до сечения обозначим переменной y1, возможные значения которой находятся в пределах от нуля до длины участка.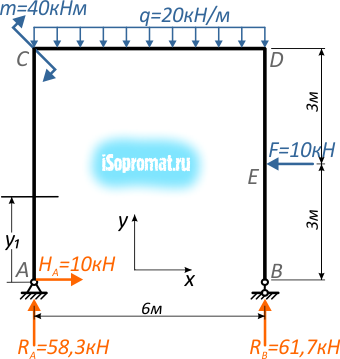
Рис. 5
Действие отброшенной части рамы заменим внутренними усилиями NI, QI и MI.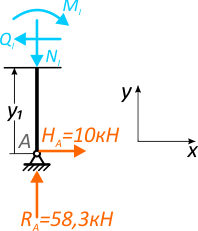
Рис. 6
Рассчитаем их: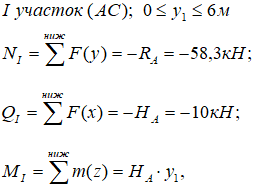
В выражении для MI переменная y1 в первой степени, а значит, эпюра на этом участке будет изображаться прямой. Для ее построения необходимы значения в двух точках.
Рассчитаем их на границах участка, в точках A и C: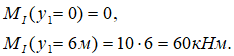
В записанных выражениях:
NI – по правилу знаков для внутренних продольных сил – отрицательна, т.к. на участке имеет место сжатие;
QI – отрицательна, т.к. стремится повернуть рассматриваемую часть рамы против хода часовой стрелки;
Для изгибающих моментов M будем отмечать то, какие слои они стремятся сжать. В данном случае момент MI сжимает правую сторону стойки.
Расчет значений внутренних силовых факторов для остальных участков рамы выполняется аналогично.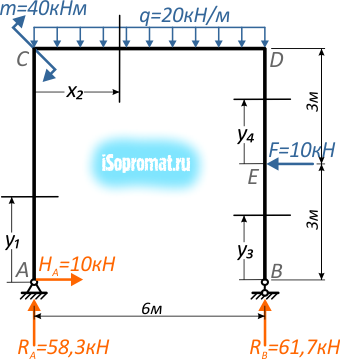
Рис. 7
На втором участке, проведя сечение (рис. 7), выберем для рассмотрения левую часть рамы (левая часть ригеля со стойкой AC).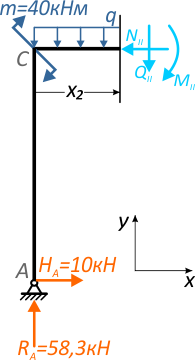
Рис. 8
Продольную силу NII здесь вызывает горизонтальная реакция HA, которая сжимает ригель.
Поперечную силу QII в сечении дают реакция RA и распределенная нагрузка q.
Изгибающий момент MII создается всеми нагрузками расположенными слева от рассматриваемого сечения.
Опорные реакции RA и HA создают момент силы. Для момента создаваемого силой HAплечо одинаково для любого положения сечения, и равно длине стойки AC, для момента реакции RA плечо переменное (y2).
О том, как рассчитать момент, создаваемый распределенной нагрузкой q можно прочитать здесь.
Записываем выражения: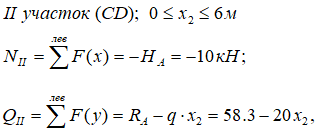
это уравнение прямой, поэтому рассчитаем значения на границах участка: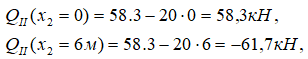
Сразу следует обратить внимание, что значения на границах участка имеют противоположные знаки, т.е. эпюра Q на данном участке пересекает базовую (нулевую) линию, следовательно, на эпюре моментов MII в этом сечении будет экстремум (эпюры Q и M дифференциально зависимы).
Запишем выражение для изгибающих моментов: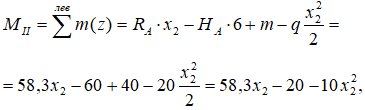
получили уравнение параболы, для построения которой требуется минимум три точки.
Двумя из них будут граничные значения момента: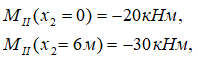
Третьей станет значение экстремума эпюры M на участке.
Короткое видео про расчёт экстремума эпюры изгибающих моментов:
Рассчитаем его:
Выражение для QII приравниваем к нулю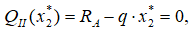
откуда находим координату сечения рамы, где Q пересекает базовую линию.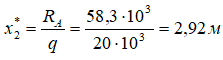
подставляем ее в выражение для MII и находим значение экстремума.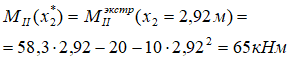
Для третьего участка рамы выбираем нижнюю часть (рис. 7):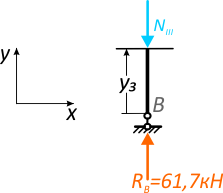
Рис. 9
Записываем выражения: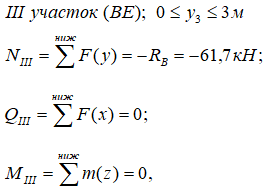
Здесь имеется только продольная сжимающая сила.
На четвертом участке (рис. 7) тоже рассмотрим нижнюю часть стойки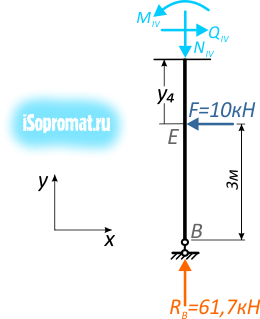
Рис. 10
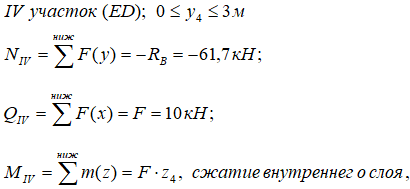
Граничные значения изгибающего момента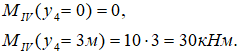
Расчет значений окончен, переходим к графическим построениям.
Построение эпюр
Для горизонтальных и вертикальных участков рамы положительные значения эпюр продольных N и поперечных сил Q будем откладывать соответственно вверх и вправо.
Как строить эпюры по рассчитанным значениям показано в нашем видео:
Эпюра внутренних продольных сил N: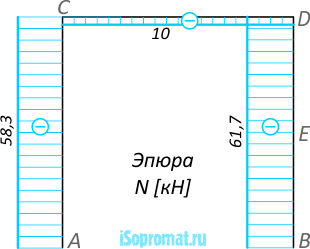 Эпюра внутренних продольных сил N рамы
Эпюра внутренних продольных сил N рамы
Рис. 11
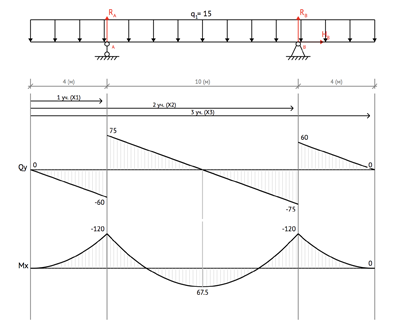
Эпюра внутренних поперечных сил Q: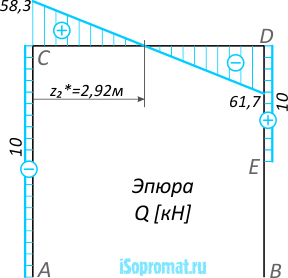 Эпюра внутренних поперечных сил Q рамы
Эпюра внутренних поперечных сил Q рамы
Рис. 12
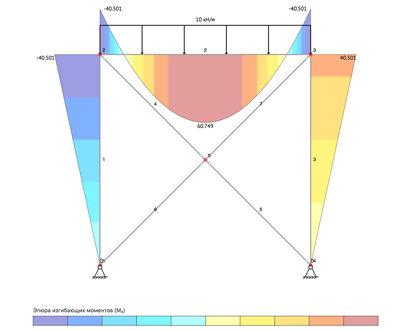
Эпюра изгибающих моментов M строится на сжатых волокнах рамы: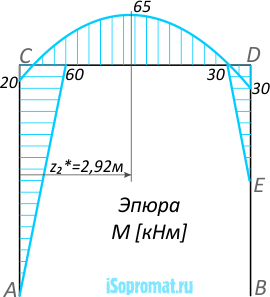 Эпюра внутренних изгибающих моментов M рамы
Эпюра внутренних изгибающих моментов M рамы
Рис. 13
Здесь следует обратить внимание на линию эпюры второго участка.
При расчете значений, граничные моменты получились отрицательными (-20 и -30кНм), т.е. они должны располагаться по одну сторону от базовой линии.
Экстремум момента положителен, следовательно, его следует откладывать по другую сторону базовой линии.
Эпюры внутренних силовых факторов для рамы построены.
Теперь необходимо выполнить их проверку.
Другие примеры решения задач >
Лекции по сопромату >
Источник
1. На рисунке проводиться ось ОХ, совпадающая с продольной осью стержня.
2. Под рисунком стержня проводятся две базовые нулевые линии, параллельно продольной оси стержня. Одна для эпюры продольной силы Nz
Вторая базовая нулевая линия для эпюры нормальных напряжений (Мпа).
3. Стержень разбивается на участки. Для границ участков проводятся вертикальные линии в точках приложения нагрузки и изменения площади поперечного сечения вниз до пересечения с базовыми нулевыми линиями. Нумерация участков начинается со свободной стороны стержня для задачи статически определимой. Если задача статически неопределимая, то нумерация выполняется слева направо.
4. Для определения значения продольной силы используется метод сечений. В середине участка проводится сечение. Указывается направление продольной силы. Положительным считается направление продольной силы, направленной от сечения (растягивает). Значение продольной силы Nz определяется из условия равновесия отсечённой части (сумма проекций на ось ох всех действующих сил равна нулю 0).
5. Вычисляем значение нормальных напряжений.
6. Положительные значения продольной силы и нормального напряжения откладываем вверх от базовой нулевой линии, отрицательные вниз.
7. Проверяем правильность решения задачи по эпюре продольной силы. В точках, где приложена сосредоточенная сила, на эпюре должен быть скачок равный значению продольной силы.
8. Условие прочности проверяем по эпюре нормальных напряжений. Максимальные напряжения, возникающие в конструкции, не должны превышать допускаемых.
Пример №1: Построить эпюры продольной силы N и нормального напряжения σ, проверить на прочность стальной стержень, закрепленный с одной стороны (статически определимая задача). Р1 = 10кН Р2 = 15кН
Р3 =15кН
=100 Мпа; А1 = F; А2 = 2F; F = 100 мм2
Решение:
Параллельно продольной оси стержня проводим две базовые нулевые линии для продольной силы и нормального напряжения.
Разбиваем стержень на участки, начиная со свободной стороны. Проводим вниз вертикальные линии в точках приложения сил и изменения площади поперечного сечения до пересечения с нулевыми линиями. Нумерация участков начинается со свободной стороны стержня.
1 участок:
— на первом участке проводим сечение, перпендикулярное продольной оси, мысленно отбрасываем большую часть и рассматриваем меньшую часть стержня. Заменяем действие отброшенной части на оставленную продольной силой N1. Положительным считается действие от сечения (растягивает).
Рассматриваем равновесие оставленной части, проецируя действующие силы на ось ОХ:
Определяем продольную силу на первом участке:
-N1+ Р1=0 следовательно N1 = Р1=10 кН
Определяем нормальное напряжение на первом участке
2 участок:
-N2+ Р1 — Р2=0 следовательно N2 = Р1-Р2 =10-15= -5 кН
3 участок:
-N3+ Р1 — Р2=0 следовательно N3 = Р1-Р2 =10-15= -5 кН
4 участок:
-N4+ Р1 — Р2+Р3=0 следовательно N4 = Р1-Р2+Р3=10-15+15= 10 кН
Рис. 10.
Метод сечений для определения продольной силы.
Для построения эпюр продольной силы и нормального напряжения задаёмся произвольным масштабом (например: одна клеточка -5 кН и -25 мегапаскалей). Строим эпюры продольной силы и нормального напряжения, откладывая положительные значения вверх от базовой нулевой линии, отрицательные вниз.
Проверяем правильность решения задачи по эпюре продольной силы, в точке приложения сосредоточенной силы на эпюре должен быть скачок, равный действующей силе.
По эпюре нормального напряжения проверяем условие прочности максимальные напряжения должны быть меньше или равны допустимым, значит прочность обеспечена.
Рис.11.
Эпюры продольной силы N и нормального напряжения σ.
СПИСОК ЛИТЕРАТУРЫ
1. Рубашкин А.Г. Лабораторные работы по сопротивлению материалов.- М.: Высшая школа, 1961.-159с.
2. Афанасьев A.M., Марьин В.А. Лабораторный практикум по сопротивлению материалов.- М.: Наука, 1975.-284с.
3. Феодосьев В.И. Сопротивление материалов.- М.: Наука, 1979.-559с.
4. Писаренко Г.С. Сопротивление материалов.- Киев.: Высшая школа, 1973.-667с.
Источник
