Сопромат курсовая работа растяжение сжатие

Ðàçìåùåíî íà https://www.allbest.ru/

Êîíòðîëüíàÿ ðàáîòà

Ðàñòÿæåíèå è ñæàòèå

Ñîäåðæàíèå

1. Îïðåäåëåíèå íàïðÿæåíèé ïðè ðàñòÿæåíèè — ñæàòèè

2. Äåôîðìàöèè ïðè ðàñòÿæåíèè-ñæàòèè è çàêîí Ãóêà

3. Îïðåäåëåíèå ïåðåìåùåíèé äëÿ äåôîðìàöèè ïðè ðàñòÿæåíèè — ñæàòèè

4. Íàïðÿæåííîå ñîñòîÿíèå ïðè ðàñòÿæåíèè-ñæàòèè è çàêîí ïàðíîñòè êàñàòåëüíûõ íàïðÿæåíèé

5. Äîïóñêàåìûå íàïðÿæåíèÿ, êîýôôèöèåíò çàïàñà è ðàñ÷åòû íà ïðî÷íîñòü ïðè ðàñòÿæåíèè- ñæàòèè

1. Îïðåäåëåíèå íàïðÿæåíèé ïðè ðàñòÿæåíèè-ñæàòèè

Ðàñòÿæåíèåì èëè ñæàòèåì áóäåì íàçûâàòü òàêîå íàãðóæåíèå ñòåðæíÿ, êîãäà â ïîïåðå÷íûõ ñå÷åíèÿõ âîçíèêàåò ëèøü îäèí âíóòðåííèé ñèëîâîé ôàêòîð — íîðìàëüíàÿ ñèëà.

ðàñòÿæåíèå ñæàòèå äåôîðìàöèÿ ïðî÷íîñòü

Ðèñ.1

Äëÿ îïðåäåëåíèÿ ïðîäîëüíûõ ñèë èñïîëüçóåì ìåòîä ñå÷åíèé. Ïðîâåäåì ñå÷åíèå à-à è ñïðîåêòèðóåì âñå ñèëû, äåéñòâóþùèå íà íèæíåþ ÷àñòü ñå÷åíèÿ, íà îñü ñòåðæíÿ. Ïðèðàâíèâàÿ ñóììó ïðîåêöèè ê íóëþ, íàéäåì:

N1=-3F

Ìèíóñ ïîêàçûâàåò, ÷òî äåéñòâóåò ñæàòèå.

Íà ó÷àñòêå À- (â ñå÷åíèè â-â):

N2=5F

Íàãëÿäíîå ïðåäñòàâëåíèå î çàêîíå èçìåíåíèÿ ïðîäîëüíûõ ñèë ïî äëèíå äàåò ýïþðà ïðîäîëüíûõ ñèë.

Ðèñ. 2

Åñëè íà ïîâåðõíîñòè ïðèçìàòè÷åñêîãî ñòåðæíÿ íàíåñòè ïðÿìîóãîëüíóþ ñåòêó, òî ïîñëå äåôîðìàöèè ëèíèè îñòàíóòñÿ âçàèìíî ïåðïåíäèêóëÿðíûìè.

(z)-?

Âñå ãîðèçîíòàëüíûå ëèíèè (c-d) ïåðåìåñòÿòñÿ âíèç, îñòàâàÿñü ãîðèçîíòàëüíûìè è ïðÿìûìè. Ìîæíî ïðåäïîëîæèòü, ÷òî âíóòðè ñòåðæíÿ áóäåò òàêàÿ æå êàðòèíà. Ýòî ãèïîòåçà Áåðíóëè èëè ãèïîòåçà ïëîñêèõ ñå÷åíèé: «Ïëîñêîå ñå÷åíèå, ïåðïåíäèêóëÿðíîå îñè ñòåðæíÿ ïîñëå äåôîðìèðîâàíèÿ îñòàåòñÿ ïëîñêèì è ïåðïåíäèêóëÿðíûì îñè ñå÷åíèÿ».

Íà ýòîì îñíîâàíèè ñ÷èòàåì, ÷òî ïîïåðå÷íàÿ ñèëà ðàâíîìåðíî ðàñïðåäåëåíà ïî ñå÷åíèþ.

Ýòà ãèïîòåçà ñïðàâåäëèâà, â ïåðâóþ î÷åðåäü, äëÿ ñòåðæíåâûõ êîíñòðóêöèé.

Èíòåíñèâíîñòü ïîïåðå÷íîé ñèëû — íîðìàëüíîå íàïðÿæåíèå:

2. Äåôîðìàöèè ïðè ðàñòÿæåíèè-ñæàòèè è çàêîí Ãóêà

Îïûòû ïîêàçûâàþò, ÷òî ïðè ðàñòÿæåíèè äëèíà ñòåðæíÿ óâåëè÷èâàåòñÿ, à ïîïåðå÷íûå ðàçìåðû óìåíüøàþòñÿ. Ïðè ñæàòèè íàîáîðîò.

Ðèñ.3

(2)-îòíîñèòåëüíîå óäëèíåíèå èëè ëèíåéíûå äåôîðìàöèè.

Äëÿ ìíîãèõ êîíñòðóêöèîííûõ ìàòåðèàëîâ ïðè íàãðóæåíèè äî îïðåäåëåííûõ ïðåäåëîâ îïûòû ïîêàçûâàþò ëèíåéíóþ çàâèñèìîñòü ëèíåéíûõ äåôîðìàöèé îò íîðìàëüíûõ íàïðÿæåíèé.

(3)- çàêîí Ãóêà.

Å- ìîäóëü ïðîäîëüíîé óïðóãîñòè èëè óïðóãîñòè ïåðâîãî ðîäà.

Çíà÷åíèÿ ìîäóëÿ óïðóãîñòè äëÿ íåêîòîðûõ ìàòåðèàëîâ (â ÌÏà):

ñòàëü- 2.105-2.2.105;

òèòàí- 1.1.105;

àëþìèíèé- 0.675. 105;

ìåäü- 1.105;

ñòåêëîïëàñòèê- 0.18.105-0.4.105;

Ïîñëå ïîäñòàíîâêè (1) è (2) â (3):

= (4)

Ìåæäó ïðîäîëüíîé å è ïîïåðå÷íûì åt äåôîðìàöèÿìè ñóùåñòâóåò ñëåäóþùàÿ ýêñïåðèìåíòàëüíàÿ çàâèñèìîñòü:

åt=íå; (5)

í- êîýôôèöèåíò ïîïåðå÷íîé äåôîðìàöèè (êîýôôèöèåíò Ïóàññîíà).

Åñëè ðàññìàòðèâàòü ïðîèçâîëüíî îðèåíòèðîâàííûé ïðÿìîóãîëüíèê ÀÂÑÄ, òî ñòîðîíû åãî óäëèíÿþòñÿ, à ñàì ïðÿìîóãîëüíèê ïîä äåéñòâèåì êàñàòåëüíûõ íàïðÿæåíèé ïåðåíîñèòñÿ è ïðåâðàùàåòñÿ â ïàðàëëåëîãðàìì. Óãëû À è Ñ óìåíüøàòñÿ, à  è Ä óâåëè÷àòñÿ.

Èçìåíåíèå ïðÿìîãî óãëà íàçûâàåòñÿ óãëîâîé äåôîðìàöèåé èëè óãëîì ñäâèãà.

Íàéäåì óãëà ïîâîðîòà îòðåçêîâ ÀÂ è ÀÄ..

Óãîë ïîâîðîòà ïîä äåéñòâèÿì ïðîäîëüíîãî óäëèíåíèÿ:

=

Óãîë ïîâîðîòà ïîä äåéñòâèåì ïîïåðå÷íîãî ñóæåíèÿ:

Äëÿ îïðåäåëåíèÿ óãëà ïîâîðîòà ÀÄ âìåñòî á íóæíî èñïîëüçîâàòü

Óãëîâàÿ äåôîðìàöèÿ èëè óãîë ñäâèãà:

Èëè ââåäÿ ìîäóëü óïðóãîñòè G èëè ìîäóëü óïðóãîñòè âòîðîãî ðîäà:

(1)

(2)

3. Îïðåäåëåíèå ïåðåìåùåíèé äëÿ äåôîðìàöèè ðàñòÿæåíèå-ñæàòèå

Ðèñ. 4

dz; N(z)

Îïðåäåëèì óäëèíåíèÿ áåñêîíå÷íî ìàëîãî ó÷àñòêà.

ÅÀ (Z) — õàðàêòåðèçóåò ñòåïåíü ñêëîííîñòè äàííîãî ó÷àñòêà ê äåôîðìèðîâàíèþ.

Ïðè íàëè÷èè íåñêîëüêèõ ó÷àñòêîâ ñ ðàçëè÷íûìè ôóíêöèÿìè îò Z, ìû äîëæíû ó÷åñòü âêëàä êàæäîãî ó÷àñòêà, êîòîðûå ðàñïîëîæåíû ìåæäó æåñòêèì çàêðåïëåíèåì è ðàññìàòðèâàåìûì ó÷àñòêîì:

Îïðåäåëåíèå ïðîäîëüíûõ ïåðåìåùåíèé ïðè ïîñòîÿííûõ â ïðåäåëàõ ó÷àñòêà ïðîäîëüíûõ ñèëàõ.

Ýòîò ñëó÷àé âñòðå÷àåòñÿ äîâîëüíî ÷àñòî.

Òîãäà

4.Íàïðÿæåííîå ñîñòîÿíèå ïðè ðàñòÿæåíèè-ñæàòèè è çàêîí ïàðíîñòè êàñàòåëüíûõ íàïðÿæåíèé

Äëÿ ïîëíîãî ñóæäåíèÿ î ïðî÷íîñòè ìàòåðèàëà íåîáõîäèìî óìåòü îïðåäåëÿòü íàïðÿæåíèå äåéñòâóþùèå ïî ëþáîìó íàêëîííîìó ñå÷åíèþ ðàñòÿíóòîãî ýëåìåíòà.

Ðèñ. 5

;

Ïðîåêòèðóÿ âñå ñèëû íà íàïðàâëåíèå ó0:

óáÀá-ó1Àcosá=0

óá=ó1cos2á; (6)

Ïðîåêòèðóÿ âñå ñèëû íà íàïðàâëåíèå ôá :

ôáÀá-ó1Àcosá=0

; (7)

ïðè ;

ïðè ;

-çàêîí ïàðíîñòè êàñàòåëüíûõ íàïðÿæåíèé.

Çàêîí ïàðíîñòè êàñàòåëüíûõ íàïðÿæåíèé: íà äâóõ âçàèìíî ïåðïåíäèêóëÿðíûõ ïëîùàäêàõ äåéñòâóþò îäèíàêîâûå êàñàòåëüíûå íàïðÿæåíèÿ, êîòîðûå íàïðàâëåíû ëèáî ê îáùåìó ðåáðó, ëèáî îò ýòîãî ðåáðà.

Ðèñ.6

Ýòîò çàêîí èìååò ìåñòî è äëÿ îáúåìíîãî íàïðÿæåííîãî ñîñòîÿíèÿ.

Îïðåäåëèì íàïðÿæåíèå íà íåêîòîðîé íàêëîííîé ïëîùàäêå, êîòîðàÿ ðàñïîëîæåíà ïîä óãëîì á ê ïëîñêîñòè íîðìàëüíîãî ñå÷åíèÿ. Ïîëíîå íàïðÿæåíèå íà ýòîé ïëîùàäêå îáîçíà÷èì ÷åðåç p.

Ðèñ. 7

Èç óñëîâèÿ ðàâíîâåñèÿ ñèë:

;

(1)

Ðàñêëàäûâàåì ýòî íàïðÿæåíèå íà íîðìàëüíóþ ê íàêëàäíîé ïëîùàäêå è êàñàòåëüíóþ ñîñòàâëÿþùèå (óá è ôá).

óá=pcosá ôá=psiná

èëè ñ ó÷åòîì (1):

(2)

Âûäåëèì â îáëàñòè, ïðèìûêàþùåé ê òî÷êå À, ïðÿìîóãîëüíèê ÀÂÑÄ.

Ðèñ. 8

;

;

(3)

Çàêîí ïàðíîñòè êàñàòåëüíûõ íàïðÿæåíèé: âåëè÷èíû êàñàòåëüíûõ íàïðÿæåíèé íà âçàèìíî ïåðïåíäèêóëÿðíûõ ïëîùàäêàõ ðàâíû è íàïðàâëåíû ëèáî ê îáùåìó ðåáðó ëèáî îò ðåáðà.

Ýòîò æå ðåçóëüòàò ìîæíî ïîëó÷èòü èç óñëîâèÿ ðàâíîâåñèÿ — ìîìåíò îò ðàâåí ìîìåíòó .

;

.

5. Äîïóñêàåìûå íàïðÿæåíèÿ, êîýôôèöèåíò çàïàñà è ðàñ÷åòû íà ïðî÷íîñòü ïðè ðàñòÿæåíèè- ñæàòèè

Òàêèì îáðàçîì, óñëîâèÿ ïðî÷íîñòè çàïèñûâàþòñÿ â âèäå:

ómax?óadm

èëè

ómax?óadm

Çäåñü:

ómax- äîïóñêàåìîå çíà÷åíèå íîðìàëüíîãî íàïðÿæåíèÿ;

ôadm- äîïóñêàåìîå çíà÷åíèå êàñàòåëüíîãî íàïðÿæåíèÿ.

Äîïóñêàåìûå íàïðÿæåíèÿ çàâèñÿò îò ìàòåðèàëà è óñëîâèé ðàáîòû ðàññ÷èòûâàåìîãî ýëåìåíòà êîíñòðóêöèè. Ýòè âåëè÷èíû äîëæíû áûòü âûáðàíû òàêèì îáðàçîì, ÷òî áû áûëà îáåñïå÷åíà íîðìàëüíàÿ ýêñïëóàòàöèÿ êîíñòðóêöèè.

Çäåñü äåéñòâóþò äâà ôàêòîðà:

Ôàêòè÷åñêèå íàãðóçêè, äåéñòâóþùèå íà äåòàëü.

Ñâîéñòâà ìàòåðèàëîâ ìîãóò çíà÷èòåëüíî îòëè÷àòüñÿ îò ïðèíÿòîãî â ðàñ÷åòàõ.

Òàêèå ôàêòîðû êàê ïåðåãðóçêà, íåîäíîðîäíîñòü ìàòåðèàëà è äðóãèå íîñÿò ÷àùå âñåãî ñëó÷àéíûé õàðàêòåð è ïðåäâàðèòåëüíî íå ìîãóò áûòü ó÷òåíû.

Ñ öåëüþ îáåñïå÷åíèÿ áåçîïàñíîé ðàáîòû êîíñòðóêöèè, äîïóñêàåìûå íàïðÿæåíèÿ äîëæíû áûòü íèæå ïðåäåëüíûõ, ïðè êîòîðûõ ìîæåò ïðîèçîéòè ðàçðóøåíèå (õðóïêèå ìàòåðèàëû) èëè ïîÿâèòñÿ ïëàñòè÷åñêèå äåôîðìàöèè (ïëàñòè÷åñêèå ìàòåðèàëû).

Çäåñü: óu- ïðåäåë ïðî÷íîñòè;

óy- ïðåäåë òåêó÷åñòè.

Êîýôôèöèåíò çàïàñà ðàâåí îòíîøåíèþ ïðåäåëüíûõ íàïðÿæåíèé ê äîïóñòèìûì. Íàçíà÷åíèå êîýôôèöèåíòà çàïàñà çàäà÷à ñïåöèàëüíûõ êóðñîâ êîíñòðóêöèÿ è ïðîåêòèðîâàíèÿ äåòàëè ïðèáîðîâ è ò.ä.

Ðàñ÷åòû íà ïðî÷íîñòü:

À. Ïðîåêòèðîâàííûé:

çàäàíà íàãðóçêà F;

èçâåñòåí ìàòåðèàë è äîïóñêàåìîå íàïðÿæåíèå óadm.

Íåîáõîäèìî îïðåäåëèòü ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ À.

Á. Ðàñ÷åòû íà ïðî÷íîñòü:

çàäàíà íàãðóçêà F è ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ À;

èçâåñòåí ìàòåðèàë è äîïóñêàåìûå íàïðÿæåíèÿ óadm.

Íåîáõîäèìî îöåíèòü ïðî÷íîñòü êîíñòðóêöèè:

Îïðåäåëèòü íîðìàëüíîå íàïðÿæåíèå:

Óñëîâèå ïðî÷íîñòè âûïîëíÿåòñÿ, åñëè:

ó?óadm.

Â. Ðàñ÷åò íåñóùåé ñïîñîáíîñòè:

çàäàíû ðàçìåðû ñå÷åíèÿ;

çàäàí ìàòåðèàë.

Îïðåäåëèòü ïðåäåëüíóþ íàãðóçêó: F=N=Aóadm.

Ëèòåðàòóðà

1.Àëåêñàíäðîâ À.Â. è äð. Ñîïðîòèâëåíèå ìàòåðèàëîâ: Ó÷åáíèê äëÿ ñò-òîâ âóçîâ — 2-å èçä., èñïð. — Ì.: Âûñøàÿ øêîëà, 2008. — 559 ñ.

2.Áîÿðøèíîâ, Ñ.Â. Îñíîâû ñòðîèòåëüíîé ìåõàíèêè ìàøèí — Ì. : Ìàøèíîñòðîåíèå, 2006. — 456 ñ.

3.Ãàôàðîâ Ð.Õ. ×òî íóæíî çíàòü î ñîïðîòèâëåíèè ìàòåðèàëîâ: Ó÷åáíîå ïîñîáèå äëÿ âóçîâ îáó÷. ïî íàïðàâëåíèÿì ïîäãîò. è ñïåö. â îáëàñòè òåõíèêè è òåõíîëîãèè — Ì.: Ìàøèíîñòðîåíèå, 2007. — 275 ñ.

4.Äàðêîâ, À.Â. Ñîïðîòèâëåíèå ìàòåðèàëîâ. — Ì. : Âûñøàÿ øêîëà, 2007. — 623 ñ.

5.Ìèðîëþáîâ È.Í. è äð. Ïîñîáèå ïî ðåøåíèþ çàäà÷ ïî ñîïðîòèâëåíèþ ìàòåðèàëîâ : ó÷åáíîå ïîñîáèå äëÿ òåõíè÷åñêèõ âóçîâ. — Ì. : Âûñøàÿ øêîëà, 2007. — 399 ñ.

6.Ñòåïèí Ï.À. Ñîïðîòèâëåíèå ìàòåðèàëîâ. — Ì. : Âûñøàÿ øêîëà, 2008. — 303 ñ.

7.Ôåîäîñüåâ Â.È. Ñîïðîòèâëåíèå ìàòåðèàëîâ: Ó÷åáíèê äëÿ ñòóä-îâ âûñø.òåõí.ó÷åá.çàâ. — 10-å èçä., ïåðåðàá. è äîï. — Ì.: Èçä-âî ÌÃÒÓ èì. Í.Ý. Áàóìàíà, 2008. — 588 ñ.

Ðàçìåùåíî íà Allbest.ru

Задача № 1

Тема: Расчет на прочность статически определимых систем при растяжении и сжатии

Требуется:

1. Построить эпюру продольного усилия Ni

2. По условию прочности подобрать размер поперечного сечение «а», если =160 МПа

3. Для рассчитанного размера поперечного сечения построить эпюру нормальных напряжений

4. Построить эпюру осевых перемещений W и найти наибольшую величину относительных деформаций , если

5. Определить потенциальную энергию упругих деформаций U

Дано: 7

Р1
= 50 кН;
l
1
=
3 м
; Ø
a 2a

Р
2
=65 кН
; l2
=
2 м
; Ø2a a 2a

Р
3
=40 кН
; l3
=
3 м
; a

Р4
=10 кН;
l
4
=
1м
; D C B A

Формы сечения: Ra
P4
P3
P2
P1

А1
№ 11 А3
№ 4

А2
№ 9 А4
№ 7
IV III II I

l 1
l2
l3
l4

Ni
= ? ; = ? ; = ?; N1
P1

= ? ; “a
” = ? ; 45 55

15

+ Эп.N (kH)

—

16 50

3,69 2

+ Эп.σ(МПа)

—

13

1,99 2,986 3,534 6,9

Эп.∆l
(мм) +

Решение:

Определяется сила реакции опор RА из уравнения статики:

Делим на 4 участка, обозначая их римскими цифрами (I, II, III, IV), а также характерные сечения через заглавные буквы (А, В, С, D, Е).

Определяется продольная сила на каждом участке методом сечения:

Строится эпюра продольных сил Ni

Определяется площадь поперечных сечений на каждом участке

А1=а*а=а2

А2=2а*а=2а2

А3=2а*2а=4а2

Определяется нормальное напряжение на каждом участке через 1/а2

Определяется максимальное значение нормального напряжения, не превышающее допускаемого напряжения, равное 160 МПа:

Максимальное значение напряжения на третьем участке

Находится значение «а»:

Принимается а = 19,4мм

Определяются действительные значения площадей поперечных сечений:

Определяются истинные значения нормального напряжения на каждом участке:

10. Строится эпюра нормального напряжения

11. Определяется относительная продольная деформация на каждом участке:

, где Е = 2 105МПа

12. Определяется относительная продольная деформация по сечениям:

13. Определяется относительное удлинение и строится эпюра этих значений (Рис 1д):

Определяется максимальное значение относительного удлинения:

14. Определяется удельная потенциальная энергия

15. Определяется полная удельная потенциальная энергия

16. Определяется относительная погрешность нормального напряжения:

Задача №2

Тема: Расчет на прочность статически неопределимых систем при сжатии и растяжении

Дано:

Схема бруса

Размеры и нагрузки

Материал брусьев – сталь 3

Допускаемое напряжение

Модуль продольной упругости

Требуется:

Определить допускаемую нагрузку для ступенчатого бруса

Дано:

l
= 30 см
= 0,3 м = 300 мм

А = 10 см2
=

К = 0,15

[Р] = ?

Эп.
N
(
kH
) Эп.
σ
(
kH
) Эп.
l
(мм)

Ra

+ — + — + —

A A

1.5l 3A
I 255 53

0,02

B 2A
II 133
В

l 0,047

C

C 425
С

1.5l 4P 4A
III 66,4 0,066

D

D

l
A
IV 255 159

E
0,035

E

∆
R
e

Решение:

Составляется уравнение статики

Составляется уравнение совместности деформации УСД:

— от заданных сил

— УСД (1)

Определяются продольные силы на каждом участке:

=? когда нет RE

Находим относительное удлинение на каждом участке

Определяется — относительное удлинение силы реакции опор, когда нет сил Р и 2Р:

Подставляем значения и в уравнение (1)

Подставляем значение силы в уравнение статики

Определяем значения продольных сил, подставляя значения

Определяется значение нормального напряжения на каждом участке

Находим максимальное значение нормально напряжения

Принимаем Р = 170 кН

Определяются действительные значения продольных сил:

10. Определяются истинные значения нормального напряжения на каждом участке :

Находим относительное удлинение

Находим относительное удлинение по сечениям

Определяем относительное удлинение

По заданной формуле вычисляем значение зазора , оно должно соответствовать значению

Проверка

Задача № 3

Тема: Расчет на прочность статически неопределимых систем при растяжении и сжатии.

Требуется:

Найти усиление и напряжение в стержнях, выразив через силу Р1

Определить допускаемую нагрузку [Р], если [σ] = 160 МПа

Найти предельную нагрузку Рпр, если [σ1] = 240 МПа и h1 = 1,5

Сравнить величины допускаемых нагрузок Рпр и Р, для чего найти их отношения.

Дано:

А=14см2 = 14·10 — 4м

а=2,3м

в=2,7см

с=1,7см

[σ] =160 МПа

hТ = 1,5

Найти: Р=?, РТ =?, [РТ] =?

Решение.

1. Составляется уравнение статики для стержневой системы

1. Σ Мi = 0; Ν1·a-P(a+c) +N2cos 45·b =0

2. Σ Zi =0; Z0 +Ν2· cos45 = 0

3. Σ Yi =0; Y0 + Ν1– P — N2·cos 45 = 0

В три уравнения равновесия входят четыре неизвестные силы, и, следовательно, задача является статически неопределимой. Для составления уравнения рассмотрим деформацию конструкции.

2. Рассмотрим подобие двух треугольников ;

Рассмотрим для нахождения деформации системы.

OB=b OA=a

y0
N1
В

N2
Р P

B1
∆l1

B2
O A

B A1
∆l2

3. Подставляем в уравнение моментов и выражаем их через Р

4. Находим значения нормальных напряжений σ1, σ2

σ1 =

σ1 =

Принимаем

5. Находим действительные значения Ni

6. Находим действительные значения σi

σ1 = =678,57=160МПа

σ2 = =339,29=79,7МПа

7. Определяем предельную нагрузку Pпр, исходя из условия равновесия

Σ Мi = 0; Ν1·а– Р·(a+c) + N2cos 45·b =0, где N1 = σт · А, и N2 = σт · 2А; σт=240МПа

8. Находим предельно допускаемую нагрузку

Задача № 4

Тема: Расчет статически определимых брусьев на прочность и жесткость при кручении.

Дано:

Схема бруса.

Размеры нагрузки.

Требуется:

Рассчитать брус на прочность и жесткость

Построить эпюры крутящих моментов, касательных напряжений и углов поворота.

Дано:

m1 = 400 Н∙м

m2 = 1200 Н∙м

m3 = 2400 Н∙м

m4 = 400 Н∙м

m5 = m5 Н∙м

[τ] = 40 МПа

[θ] = 0,5

d = 0,5

d1 = 1.5b

d2 = 2b

d3 = 2.5b

a = 0.3 м

Найти: Т, τ, θ — ?

Решение.

Составим уравнение статики:

Σ Мi = 0

m1 – m2 – m3 + m4 + m5 = 0

m5 = — m1 + m2 + m3 – m4 = — 400 + 1200 + 2400 – 400 = 2800 H·м

T1 = + m1 = 400 H·м

T2 = m1 – m2 = 400 – 1200 = — 800 H·м

T3 = m1 – m2 – m3 = — 800 – 2400 = — 3200 H·м

T4 = m1 – m2 – m3 = — 800 – 2400 = — 3200 H·м

T5 = m1 – m2 – m3 + m4 = – 2800 H·м

T6 = m1 – m2 – m3 + m4 + m5 = 0 H·м

Определяем полярный момент сопротивления на каждом участке Wpi:

Определяется касательное напряжение на каждом участке по формуле , выражая каждое значение через 1/b3

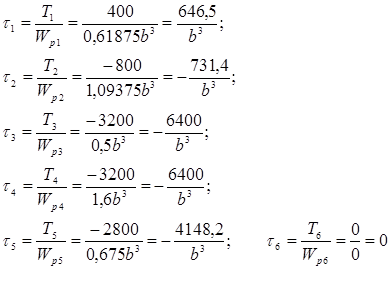
Определяем максимальное значение касательного напряжения из пяти значений:

τmax = max {τ1, τ2, τ3, τ4, τ5} ≤ [τ] ;

τ3 ≤ [τ]

Определяется полярный момент инерции по данной формуле на каждом участке:

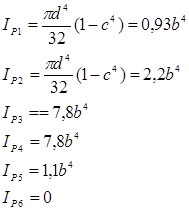
5. Определяем относительный угол закручивания по формуле

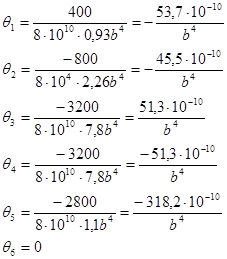
Определяем максимальное значение:

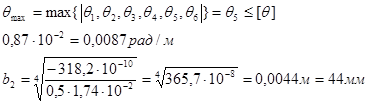
Примем максимальное значение из полученных значений b:

b≥{|b1|,|b2|} = b1 = 54,3 мм = 54,3·10 — 3 м = 55мм

6. Определяем действительные значения касательного напряжения τi:

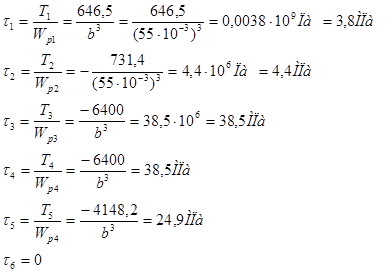
Определяем действительные значения относительного угла закручивания θi:

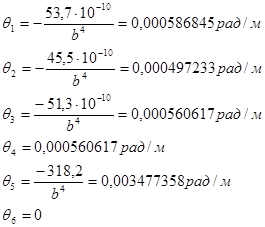
Определяем по формуле значение перемещения

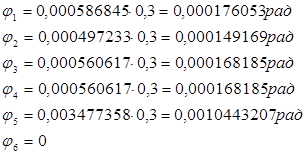
Находим числовые значения перемещения Δφi по сечениям:

φА = 0

φВ = φА + φ1 = 0 + 0,000176053 = 0,000176053 рад;

φС = φВ + φ2 = 0,000176053 + 0,000149169 = 0,000325222 рад;

φD = φС + φ3 = 0,000325222 + 0,000168185 = 0,000493407 рад;

φЕ = φD + φ4 = 0,000493407 + 0,000168185 = 0,000661592 рад;

φF = φЕ + φ5 = 0,000661592 + 0,003477358 = 0,00413895 рад;

φG = φF + φ6 = 0,00413895 + 0= 0,00413895 рад.