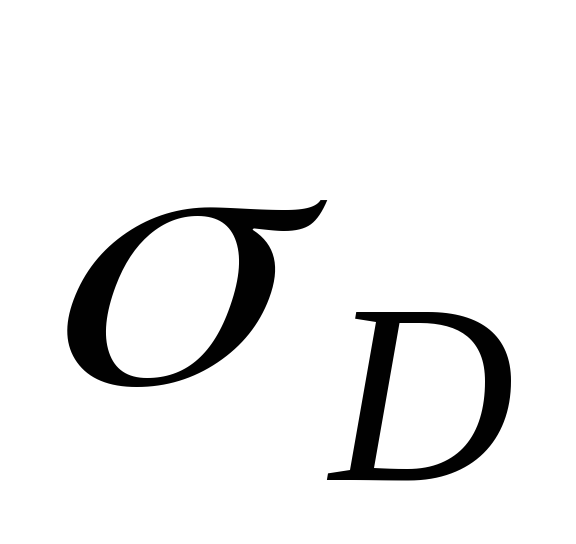Сложный изгиб с растяжением
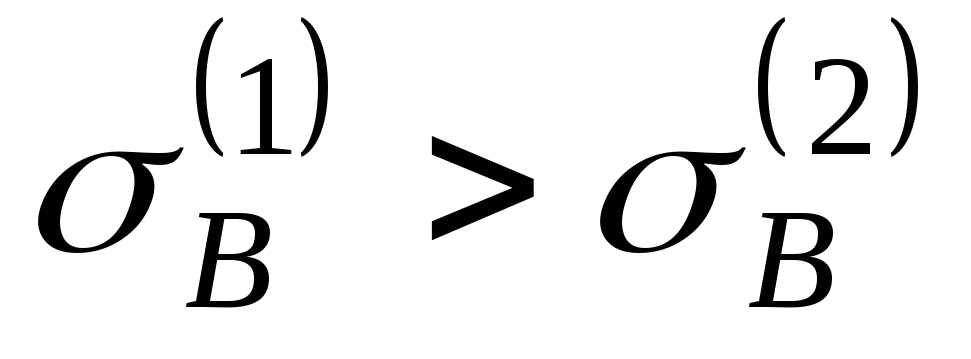









Изгиб с растяжением – частный случай сложного сопротивления, при котором на брус действуют продольные и поперечные нагрузки, пересекающие ось бруса. В общем случае в поперечных сечениях возникают пять внутренних усилий: действующие в двух плоскостях изгибающие моменты Mz, My, поперечные силы Qz, Qy, а также продольная сила N. Возникает сложный изгиб с растяжением или сжатием. Пренебрегая касательными напряжениями от поперечных сил Qz, Qy (для длинных балок с отношением ℓ/h > 10 их влияние незначительно), можно считать напряженное состояние в опасных точках линейным. Внецентренное растяжение или сжатие Внецентренное растяжение – частный случай изгиба с растяжением, при котором брус растягивается силами, параллельными оси бруса так, что их равнодействующая не совпадает с осью бруса, а проходит через точку Р, называемую полюсом силы. Внутренние усилия и напряжения В произвольном сечении х бруса (рис.8.7, а) методом сечений определяем внутренние усилия Рис. 8.6. Примеры деталей и узлов, работающих при внецентренном нагружении: а – болт-костыль; б – пружина сцепления; в – сварное соединение Отличны от нуля три внутренних усилия (рис. 8.7, б), от которых возникают нормальные напряжения, действующие по одной из трех пар граней (рис. 8.7, в); две другие пары граней свободны от напряжений. Имеет место линейное напряженное состояние. Напряжения в произвольной точке являются суммой трех слагаемых Учитывая, что отношение i = – радиус инерции сечения, получим О правиле знаков внутренних усилий. Формула (8.10) выведена для случая положительной растягивающей силы N и изгибающих моментов Mz, My, вызывающих растягивающие напряжения в точке, принадлежащей первой четверти осей координат (где x > 0 и y > 0). Поэтому оси координат поперечного сечения бруса следует направлять так, чтобы полюс P (точка приложения силы) находился в первом квадранте. Если сила, приложенная к брусу, сжимающая, то ее числовое значение будет со знаком минус. Анализ формулы (8.10) 1. Отсутствие координаты х свидетельствует о неизменности напряжений вдоль оси бруса. 2. В случае приложения силы в центр тяжести сечения (zP = 0, yP = 0) напряжения в любой точке сечения постоянны и равны σ = F/A, то есть центральное растяжение является частным случаем внецентренного. Рис. 8.7. Схема к определению внутренних усилий и напряжений при внецентренном приложении силы 3. Независимо от значений координат полюса Р напряжение в центре тяжести сечения (yцт =0, zцт = 0), σцт = F/A. 4. Переменные z и y в первой степени, следовательно, формула (8.10) является уравнением прямой и нормальные напряжения распределяются по линейному закону, значит должна быть нейтральная линия, на которой напряжения равны нулю. Уравнение нейтральной линии при внецентренном растяжении Нейтральная линия (нейтральная ось) – геометрическое место точек, в которых нормальное напряжение в поперечном сечении равно нулю. Приравняем нулю уравнение (8.10). Поскольку F/A ≠ 0, то выражение в скобках равно нулю Переменные z, y в первой степени, следовательно, нормальные напряжения в сечении распределяются по линейной зависимости. Полученное выражение приведем к виду уравнения прямой в отрезках, где a и b – отрезки, отсекаемые линией на осях координат. В нашем случае уравнение нейтральной линии будет записано как Свободный член полученного уравнения не равен нулю, следовательно, нейтральная линия через начало координат не проходит. Отрезки, отсекаемые нейтральной линией на осях y и z, соответственно равны: По найденным значениям отрезков проводят нейтральную линию и находят точки В и С, наиболее удаленные от нее (рис. 8.9). Выполняют это простым геометрическим построением, проводя касательные к сечению, параллельные нейтральной оси. Найденные точки – опасные, поскольку напряжения в них наибольшие по величине. Рис. 8.8. Уравнение прямой в отрезках и график прямой линии, известные из школьного курса Уравнения (8.12), связывающие координаты полюса Р – точки приложения внешней нагрузки с положением нейтральной линии, являются гиперболической функцией. Чем ближе полюс Р к центру тяжести сечения (значения yP, zP уменьшаются), тем нейтральная линия проходит дальше и в пределе стремится к бесконечности. И, наоборот, по мере отдаления точки приложения силы от центра тяжести нейтральная линия асимптотически приближается к нему. Однако пересечь центр тяжести сечения нейтральная линия не может (см. анализ формулы (8.10)). В центре тяжести σцт = F/A (рис. 8.9), поскольку yцт = 0 и zцт = 0 (подставьте в (8.10)). Нейтральная линия может разделять поперечное сечение на области, в которых действуют напряжения разных знаков. Некоторые материалы (чугун, силумин, керамика, кирпичная кладка…) хорошо сопротивляются сжатию и плохо – растяжению. Поэтому необходимо уметь определять такую область приложения нагрузки, в которой не возникают напряжения разных знаков. Ядро сечения Ядро сечения – область вокруг центра тяжести сечения, при приложении нагрузки внутри которой, напряжения во всем сечении будут одного знака. Контур ядра сечения строят путем окатывания нейтральной линией контура поперечного сечения, то есть решают задачу обратную той, в которой определяли положение нейтральной линии: куда следует прикладывать силу, чтобы нейтральная линия не пересекала контур сечения, а только касалась его. Задают несколько положений нейтральной линии, касательной к сечению (например, н.л.1, н.л.2, н.л.3), определяют координаты точек пересечения этих линий с осями координат (например, zн.л.1, yн.л.1). Затем, преобразуя уравнение (11), находят Рис. 8.10. Определение координат отрезков нейтральной линии для построения ядра сечения Рис. 8.9. Эпюра напряжений в поперечном сечении Нейтральная линия соответствующие им координаты точек ядра сечения (точки 1, 2, 3): Так как при переходе нейтральной линии с одной стороны на другую (например, от н.л 3 к н.л 4) она поворачивается вокруг угловой точки сечения, то точка приложения силы перемещается по прямой (на рис. 8.10 отрезок 3 – 4), образуя контур ядра. Пример 8.4. Построить ядро сечения для круга диаметром d. Решение. Квадрат радиуса инерции круга: Задаем положение нейтральной линии 1–1, касательной к окружности. Ее координаты: Координаты точки ядра сечения: Из симметрии сечения относительно его центра тяжести следует, что при других положениях нейтральной линии на окружности диаметром d точки ядра сечения образуют концентрический с ней круг диаметром d/4. Пример 8.5. Построить ядро сечения для прямоугольника с размером сторон bЧh. Решение. Квадраты радиусов инерции: Задаем положение нейтральной линии 1-1, касательной к верхней грани прямоугольника. Ее ко- ординаты: zн.л 1 = ∞; yн.л1 = h/2. Координаты соответствующей точки ядра сечения: Аналогично для нейтральной линии 2-2: zн.л 2 = b/2; yн.л 2 = ∞. Учитывая симметрию прямоугольного сечения относительно осей z и y, задаем положения нейтральных линий на противоположных сторонах прямоугольника и получаем еще две точки. Соединяя все точки, получаем ядро сечения в виде ромба с диагоналями, равными h/3 и b/3. Пример 8.6. Построить ядро сечения для швеллера № 20. Решение. Из таблицы сортамента выпишем исходные данные и выполним рисунок швеллера. Последовательно задаем положение нейтральной линии (I-I, II-II, III-III, IV-IV), касающейся контура сечения, и вычисляем координаты точек ядра сечения. Расчеты представлены в табличном виде. Ядро сечения имеет вид четырехугольника, асимметричного относительно оси ординат. Положение ядра сечения зависит лишь от формы и размеров поперечного сечения, но не зависит от величины приложенной силы. Расчет на прочность при внецентренном нагружении Поверочный расчет выполняют, используя условие прочности Проектный расчет обладает особенностью, связанной с тем, что геометрические характеристики, входящие в условие прочности содержат искомый размер поперечного сечения в разной степени. Площадь А измеряется в м2, а моменты сопротивления W в м3. Попытка выразить искомый yн.л. = h/2 = 20/2 = 10 см; zн.л. = ∞; размер из условия прочности приводит к трансцендентной функции, то есть аналитической функции, не являющейся алгебраической. Проектный расчет выполняют методом итераций 1 [от лат. iteratio – повторение]. В первом приближении, пренебрегая одним из внутренних усилий, – продольной силой N – подбирают размер сечения только из условия прочности при изгибе. Полученный размер подставляют в исходное уравнение и выполняют следующую пробу. Процесс повторяют до тех пор, пока невязка – разность размеров последующей и предыдущей проб, не достигнет заданной наперед малости. Пример 8.7. (Винокуров А. И. Сборник задач … 5.35). Подобрать диаметр стержня выпускного клапана. При расчете использовать усилие F в момент открывания клапана в конце рабочего хода поршня. Решение. Сила давления газов на тарелку клапана 533441Н Внутренние усилия в сечении 1-1 стержня клапана (по модулю): N = F; M = F•e. Условие прочности: По обе стороны от знака неравенства искомый диаметр – имеем трансцендентное уравнение, которое решаем методом приближений: Метод последовательных приближений, при котором каждое новое приближение вычисляют исходя из предыдущего; начальное приближение выбирается в достаточной степени произвольно. Дано: p = 1,5 МПа; e = 12 мм; D = 35 мм; [σ] = 210 МПа Разность между последним и предпоследним приближениями Процесс подбора прекращаем, принимаем d = 10 мм. Проверка: Напряжения изгиба больше напряжений растяжения в 6,9 раза Пример 8.8. (Винокуров А. И. Сборник задач … 5.38.). Из расчета на прочность определить размер h скобы струбцины. Решение. Условие прочности при внецентренном растяжении плоской фигуры σ=+≤[σ] где A = b•h; W = b•h2/6; M = F(a+h/2). Условие прочности: Требуемый размер скобы: Размер h в обеих части неравенства. Полученное уравнение – трансцендентное. Решаем его методом последовательных приближений. В первом приближении принимаем h в скобках под корнем равным нулю: h0 = 0. Тогда Невязка подбора 100 25,4 % Следующее приближение 101,58 мм. Невязка подбора 100 4,5 % Следующее приближение 102,54 мм. Невязка подбора 100 0,95 % невязка менее 1 %, поэтому выходим из цикла подбора. Принимаем h = 103 мм. Проверка: Сопоставим вклады от изгиба и растяжения в общее напряжение: Напряжения от изгиба в 8,24 раза превышают напряжения от растяжения. Полученное соотношение можно сделать более благоприятным снизив долю растягивающих напряжений от изгиба за счет уменьшения плеча е изгибающего момента. На практике применяют тавровое и двутавровое сечения, смещая центр тяжести с ближе к линии действия силы и располагая больше материала в области растягивающих напряжений, к которым хрупкие материалы более чувствительны. Рис. 8.11. Примеры выполнения поперечного сечения бруса, подверженного действию внецентренного растяжения
Источник
Сложное сопротивление – одновременное действие на брус нескольких простых видов деформаций: растяжения-сжатия, сдвига, кручения и изгиба. Например, совместное действие растяжения и кручения.
Косой изгиб.
Косой изгиб – это изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных плоскостей инерции сечения бруса.
В общем случае при косом изгибе в поперечных сечениях возникают четыре внутренних силовых фактора: поперечные силы Qx, Qy и изгибающие моменты Mx , My. Таким образом, косой изгиб можно рассматривать как сочетание двух плоских поперечных изгибов во взаимно перпендикулярных плоскостях. Влиянием поперечных сил на прочность и жесткость бруса обычно пренебрегают.

Нейтральная линия при косом изгибе всегда проходит через центр тяжести сечения.
Условие прочности при косом изгибе:

где ymax, xmax — координаты точки сечения, наиболее удаленной от нейтральной оси.
Для сечений, имеющих две оси симметрии, максимальные напряжения будут в угловых точках, а условие прочности:

где Wx , Wy – осевые моменты сопротивления сечения относительно соответствующих осей.
Если материал бруса не одинаково работает на растяжение и на сжатие, то проверку его прочности выполняют по допускаемым и растягивающим и сжимающим напряжениям.
Прогибы при косом изгибе определяют, используя принцип независимости действия сил, геометрическим суммированием прогибов вдоль направления главных осей:

Изгиб с растяжением (сжатием).
При таком виде сложного сопротивления внутренние силовые факторы приводятся к одновременному действию продольной силы N и изгибающего момента M.
Рассмотрим случай центрального растяжения бруса в сочетании с косым изгибом. На консольный брус действует сила F, составляющая некоторый угол с продольной осью бруса и не лежащая ни в одной из главных плоскостей сечения. Сила приложена в центре тяжести торцевого сечения бруса:

К расчёту на прочность бруса при изгибе с растяжением:
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Разложим силу F на три составляющие. Тогда внутренние силовые факторы приобретут следующий вид:

Напряжение в произвольно выбранной точке Д, имеющей координаты (хд, уд), пренебрегая действием поперечных сил, будут определяться по формуле:

где А — площадь поперечного сечения.
Если сечение имеет две оси симметрии (двутавр, прямоугольник, круг), наибольшее напряжение определяют по формуле:

Условие прочночти имеет вид:

Также как и в случае косого изгиба, если материал бруса не одинаково работает на растяжение и на сжатие, то проверку прочности проводят по допускаемым растягивающим и сжимающим напряжениям.
Внецентренное растяжение или сжатие.
При таком виде сложного сопротивления продольная сила приложена не в центре тяжести поперечного сечения бруса.

К расчёту на прочность бруса при внецентренном растяжении
a — нагружение бруса; б — внутренние силовые факторы в поперечном сечении;
Приведём силу F к центру тяжести:

где уF , xF — координаты точки приложения силы F.
В произвольной точке Д, с координатами (хд, уд), нормальное напряжение определяется по фомуле:

Условие прочности для бруса, изготовленного из материала, одинаково сопротивляющегося растяжению и сжатию, имеет вид:

Для бруса, который неодинаково работает на растяжение и на сжатие проверка прочности по допускаемым растягивающим и сжимающим напряжениям.
Кручение с изгибом.
Сочетание деформаций изгиба и кручения характерно для работы валов машин.

Напряжения в сечениях вала возникают от кручения и от изгиба. При изгибе появляются нормальные и касательные напряжения:

Эпюры напряжений в сечении бруса при кручении с изгибом
Нормальное напряжение достигает максимума на поверхности:

Касательное напряжение от крутящего момента Mz достигает максимума также на поверхности вала:

Из третьей и четвёртой теории прочности:

При кручении с изгибом условие прочности имеет вид:

Источник
Изгиб с растяжением
(сжатием) относится к видам сложного
сопротивления первой группы. При этом
виде сложного сопротивления могут
возникнуть пять внутренних силовых
факторов: продольная сила
![]() ,
,
поперечные силы![]() и
и![]() и изгибающие моменты
и изгибающие моменты![]() и
и![]() .
.
Если пренебречь влиянием касательных
напряжений на прочность бруса, из пяти
внутренних силовых факторов остаются
три![]() .
.
Этот случай сложного сопротивления был
подробно рассмотрен в разделе 12.2
настоящего пособия. Поэтому все формулы
для нормальных напряжений и условия
прочности, полученные в разделе 12.2,
могут быть применены и к рассматриваемому
виду сложного сопротивления. Следует
отметить, что при возникновении сложного
изгиба со сжатием, брус должен обладать
большой жесткостью, т.е. не терять
устойчивость.
Рассмотрим частный
случай действия нагрузки, при котором
возникает изгиб с растяжением. Балка
консольного типа (Рис.12.15,а) с прямоугольным
поперечным сечением. Балка нагружена
наклонной силой
![]() ,
,
лежащей в вертикальной плоскости.
Разложим силу![]() не две составляющие: горизонтальную
не две составляющие: горизонтальную
составляющую![]() и вертикальную составляющую
и вертикальную составляющую![]() .
.
От вертикальной составляющей силы![]() возникает изгибающий момент
возникает изгибающий момент![]() (Рис.12.15,б),
(Рис.12.15,б),
от горизонтальной составляющей силы![]() продольная сила
продольная сила![]() (Рис12.15,в).
(Рис12.15,в).
Изгибающий момент![]() .
.
Изгибающий момент![]() меняется
меняется
по линейному закону, достигая максимального
значения в заделке, в сечении А, продольная
сила положительная и постоянная по
величине на всей длине балки.
Нормальные
напряжения в произвольно выбранной
точке сечения для рассматриваемого
частного случая определим по формуле
(12.2) при
![]() :
:
![]() .
.
(12.25)
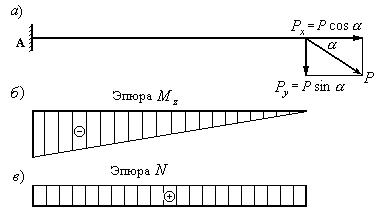
Рис.12.15
При определении
напряжений по формуле (12.25) применяем
принцип простого суммирования напряжений
от действия каждого из факторов в
отдельности. На рис.12.16 приведен
графический пример сложения напряжений.
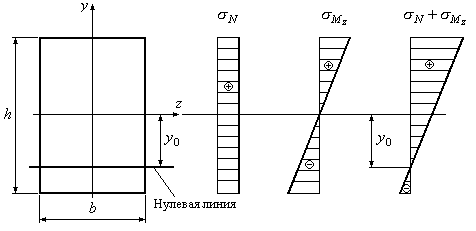
Рис.12.16
Уравнение нулевой
линии получим, приравняв нулю выражение
для напряжений:
![]() ,
,
(12.26)
откуда находим
ординату нулевой линии
![]() .
.
Максимальные
напряжения действуют в волокнах, наиболее
удаленных от нулевой линии. Условие
прочности принимает вид:
![]() .
.
(12.27)
Условие прочности
содержит две неизвестные величины –
оевой момент сопротивления
![]() и площадь поперечного сечения
и площадь поперечного сечения![]() .
.
В большинстве случаев нормальные
напряжения от изгиба больше, чем от
растяжения или сжатия, поэтому при
подборе сечения можно вначале опустить
первое слагаемое и найти приближенное
значение для момента сопротивления.
Затем подбираются размеры поперечного
сечения по найденной величине момента
сопротивления. Размеры сечения берутся
несколько большими требуемых и далее
проверяется прочность выбранного
сечения по формуле (12.27).
12.6. Внецентренное растяжение (сжатие) прямого бруса
Внецентренное
растяжение (сжатие) относится к видам
сложного сопротивления первой группы.
Этот вид деформации вызывается действием
силы, параллельной продольной оси
стержня, но не проходящей через центр
тяжести поперечного сечения.
Рассмотрим брус
с произвольной формой поперечного
сечения, на который действует сила
![]() ,
,
параллельная оси бруса и пересекающая
любое поперечное сечение в точке А.
Координаты этой точки в системе главных
осей инерции сечения обозначим![]() и
и![]() (Рис.12.17). Расстояние точки А от центра
(Рис.12.17). Расстояние точки А от центра
тяжести сечения обозначим буквой![]() назовем ексцентриситетом точки приложения
назовем ексцентриситетом точки приложения
силы.
Приложим в точках
В и 0 две пары уравновешенных системы
сил. В результате получим две пары сил:
![]() и
и![]() .
.
Кроме того, в точке 0 появится сила![]() ,
,
действующая вдоль оси![]() .
.
Эти внешние силы вызовут в произвольном
прперечном сечении, лежащем на расстоянии![]() от основания фигуры, внутренние силовые
от основания фигуры, внутренние силовые
факторы:![]() ;
;![]() ;
;![]() .
.
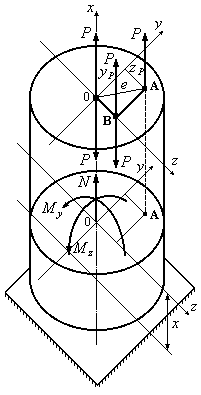
Рис.12.17
Таким образом,
напряжения в произвольной точке
поперечного сечения
![]() будут складываться из напряжений,
будут складываться из напряжений,
вызванных продольной силой![]() и напряжениями чистого изгиба, вызванных
и напряжениями чистого изгиба, вызванных
моментами![]() и
и![]() ,
,
по формуле (12.2). После несложных
преобразований эту формулу можно
преобразовать к виду, выразив внутренние
усилия через внешнюю силу![]() :
:
![]() .
.
(12.28)
Принимая во
внимание, что
![]() ;
;![]() квадраты радиусов
квадраты радиусов
инерции сечения относительно главных
осей![]() и
и![]() ,
,
формулу (12.28) преобразуем к виду:
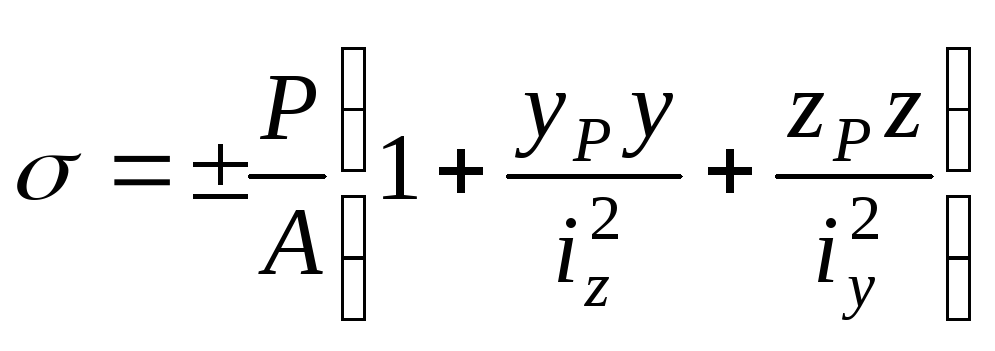 .
.
(12.29)
При определении
напряжений по формуле (12.29) знак “+”принимается для случая, если сила![]() растягивающая. При сжимающей силе
растягивающая. При сжимающей силе![]() перед скобкой в формуле (12.29) принимается
перед скобкой в формуле (12.29) принимается
знак“”.
Поскольку при
внецентренном растяжении или сжатии
возникает осевое растяжение (сжатие) и
чистый пространственный изгиб, все
поперечные сечения стержня в одинаковой
степени опасны. Опасные же точки в
поперечном сечении найдем, построив
нулевую линию. Уравнение нулевой линии
получим, если приравняем нулю напряжения,
вычисленные по формуле (12.29) в произвольной
точке нулевой линии с координатами
![]() и
и![]() :
:
![]() .
.
(12.30)
Построим нулевую
линию (Рис.12.18).
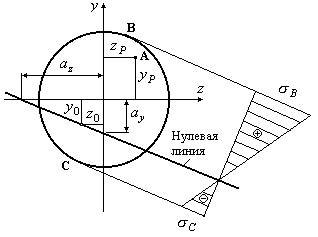
Рис.12.18
Так как координаты
нулевой линии
![]() и
и![]() входят в формулу (12.30) в первой
входят в формулу (12.30) в первой
степени, нулевая линия является прямой
линией. Следовательно, ее можно построить,
определив отрезки, которые нулевая
линия отсекает на осях координат![]() и
и![]() .
.
Для их определения зададим в формуле
(12.30) значение![]() .
.
Тогда, обозначив отрезок, который нулевая
линия будет отсекать на оси![]() через
через![]() и вводя его в формулу (2.30) вместо
и вводя его в формулу (2.30) вместо![]() ,
,
получим:
![]() .
.
(12.31)
Задавая
![]() аналогичным образом из формулы (12.30)
аналогичным образом из формулы (12.30)
получим:
![]() .
.
(12.32)
Откладываем
найденные отрезки на осях координат
(Рис.12.18) и строим нулевую линию.
Проанализируем
поведение нулевой линии при внецентренном
растяжении (сжатии):
1. Нулевая линия –
прямая линия.
2. Нулевая линия
не проходит через центр тяжести
поперечного сечения.
3. Нулевая линия
проходит через две четверти координат,
ни одной из которых не принадлежит точка
приложения силы (нулевая линия никогда
не проходит через ту четверть, в
которой лежит точка приложения
силы).
Теперь, имея нулевую
линию, проводим параллельно ей касательные
к контуру сечения и находим наиболее
напряженные точки В и С в растянутой и
сжатой зонах сечения (Рис.12.18). Напряжения
в этих точках и условия прочности имеют
вид:
![]() ;
;
(12.33)
![]() .
.
(12.34)
Координаты точек
приложения силы
![]() и
и![]() , а также координаты А и В, в которых
, а также координаты А и В, в которых
определяются напряжения, проставляются
в формулах (12.33) и (12.34) со своими знаками.
Эпюра нормальных напряжений![]() для рассматриваемого случая внецентренного
для рассматриваемого случая внецентренного
растяжения приведена на рис.12.18.
Для прямоугольного
сечения максимальные напряжения лежат
в одной из угловых точек и условие
прочности удобно использовать в таком
виде:
![]() .
.
(12.35)
Выше был рассмотрен
случай внецентренного растяжения.
Полученные формулы (12.33)-(12.35) справедливы
и для случая внецентренного сжатия при
условии, если нет опасности возникновения
продольного изгиба.
Рассмотрим несколько
примеров решения задач на внецентренное
растяжение и сжатие.
Пример 12.6. Стержень
прямоугольного профиля в точке А
подвергается действию растягивающей
силы силы
![]() кН
кН
(Рис.12.19). Определить наибольшие нормальные
напряжения в сечении стержня.
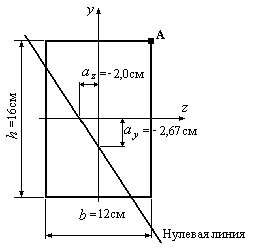
Рис.12.19
Решение:
1. Определяем
моменты инерции и квадраты радиусов
инерции сечения относительно главных
осей
![]()
и
![]() :
:
![]() см4;
см4;
![]() см4;
см4;
![]() см2;
см2;
![]() см2.
см2.
2. Определяем
отрезки, определяемые нулевой линией
на осях координат:
![]() см;
см;
![]() см.
см.
3. Строим нулевую
линию (Рис.12.19).
4. Наиболее удаленной
от нулевой линии является точка А.
Напряжения в этой точке будут наибольшими:
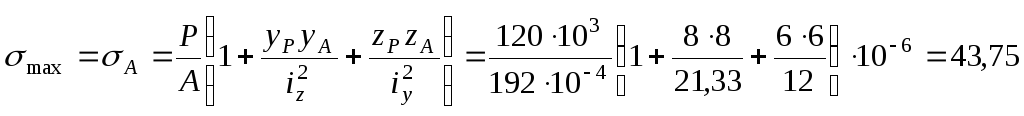 МПа.
МПа.
Пример 12.7.В
точках А двух коллонн приложены сжимающие
силы (Рис.12.20). При этом в точке С обеих
колонн сжимающие напряжения оказались
одинаковыми. Сравнить напряжения в
точках В обеих колонн.
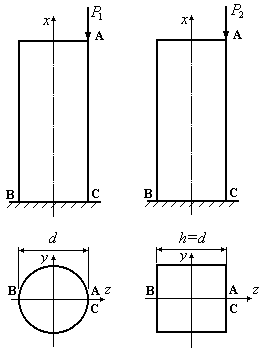
Рис.12.20
Решение:
1. Обозначим высоту
второй колонны буквой
![]() и, учитывая, что для второй колонны
и, учитывая, что для второй колонны
размер![]() ,
,
вычислим для каждой колонны квадраты
радиусов инерции сечений относительно
оси![]() .
.
Для первой (левой)
колонны:
![]() ;
;
Для второй (правой)
колонны:
![]() .
.
2. Определяем
напряжение в точке С для первой колонны:
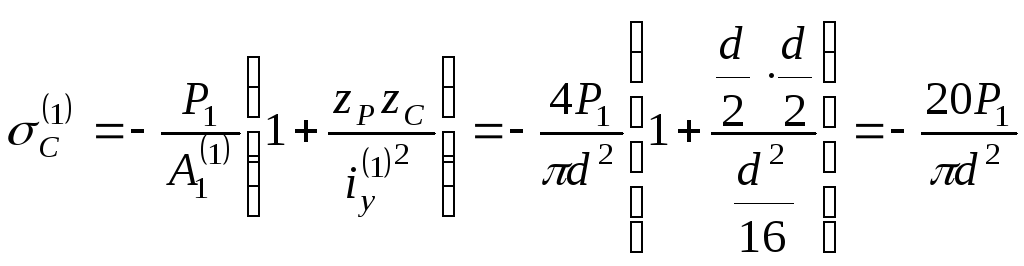 .
.
(а)
3. Определяем
напряжение в точке С для второй колонны:
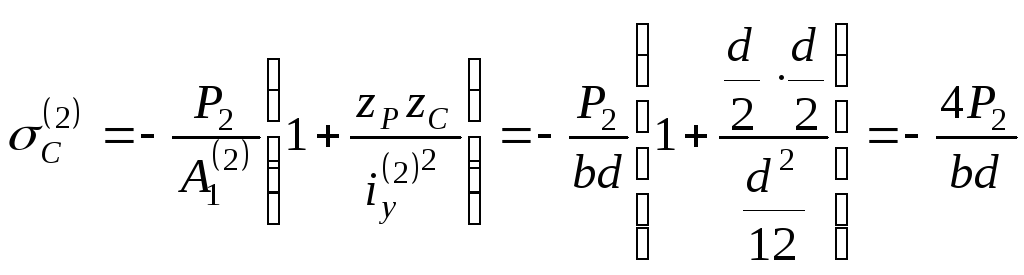 .
.
(б)
4. По условию задачи
нормальные напряжения в точке С для
обеих колонн одинаковы, т.е.
![]() .
.
Приравнивая выражения (а) и (б), выражаем
силу![]() через силу
через силу![]() :
:
![]() .
.
(в)
5. Вычисляем
нормальные напряжения в точке В сечения
для первой колонны:
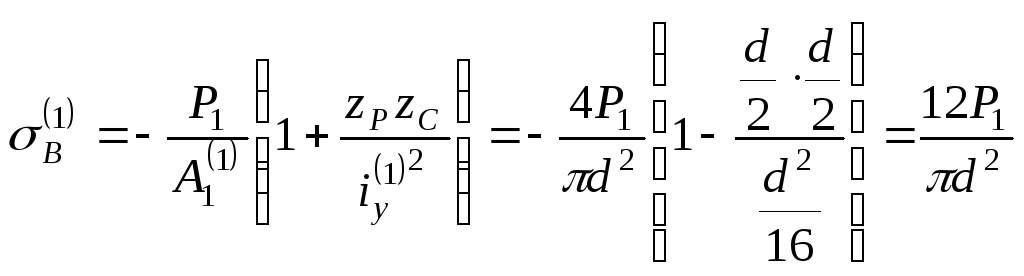 .
.
(г)
5. Вычисляем
нормальные напряжения в точке В сечения
для второй колонны:
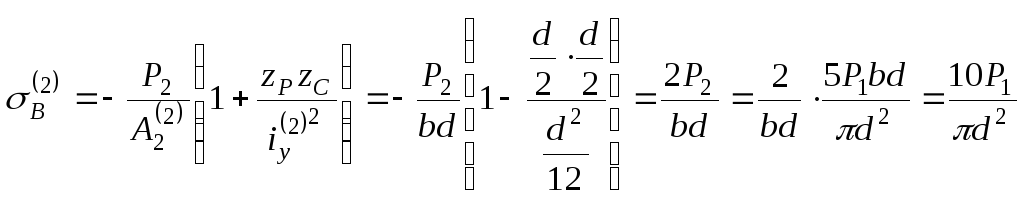 .
.
(д)
6. Напряжение
![]() .
.
Составим их отношение:
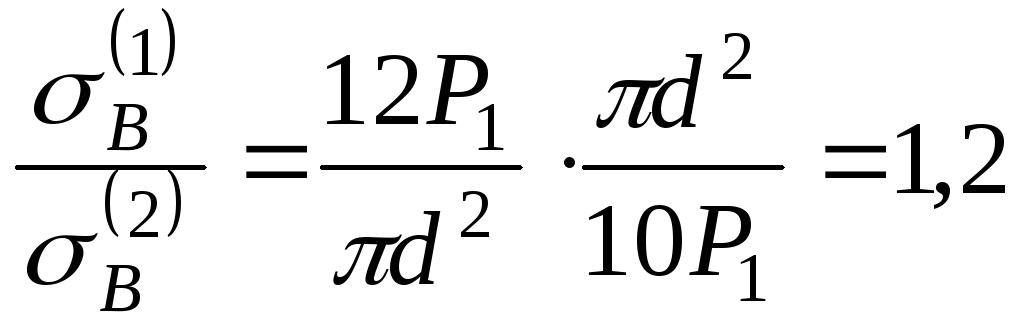
Таким образом,
напряжение в первой колонне на 20% выше,
чем во второй.
Пример 12.8.В
точках А и В колонны прямоугольного
сечения приложены одинаковые силы
(Рис.12.21а). Как изменится наибольшее
сжимающее напряжение в колонне, если
одну из сил удалить?
Решение:
1. Найдем напряжения
в колонне, когда действуют две симметрично
расположенные силы (Рис.12.21,б). Такое
приложение сил является центральным.
В этом случае нормальные напряжения от
сжатия найдем из формулы:
![]() .
.
(а)
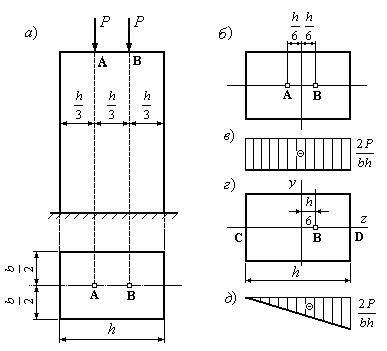
Рис.12.21
В каждой точке
поперечного сечения напряжения одинаковы.
Эпюра нормальных напряжений приведена
на рис.12.21в.
2. Удалим одну из
сжимающих сил, например, силу, действующую
в точке А. Оставшаяся сила
![]() ,
,
действующая в точке В сечения, вызовет
внецентренное сжатие. Установим опасные
точки сечения. С этой целью построим
нулевую линию. Уравнение нулевой линии
имеет вид:
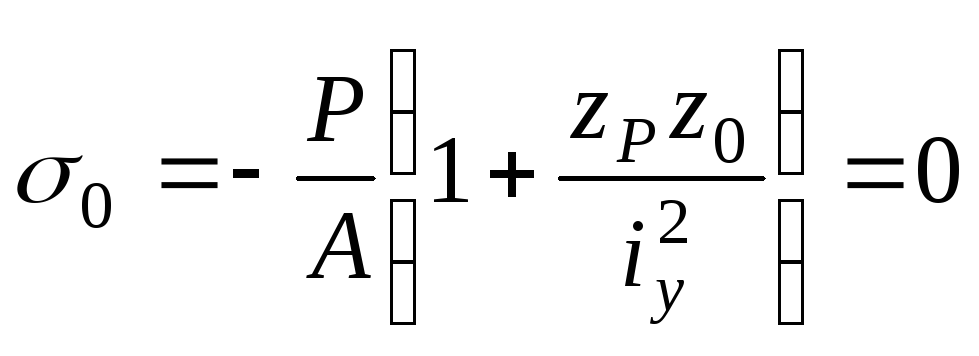 .
.
Решая это уравнение
относительно
![]() ,
,
получим:
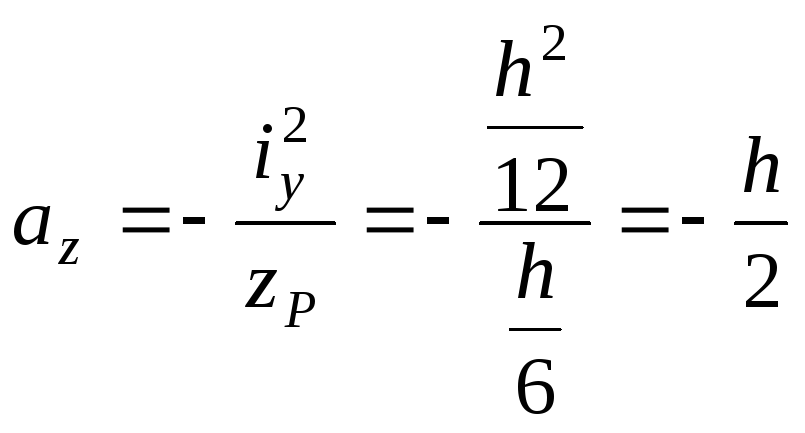 .
.
Нулевая линия
совпадает с левой кромкой сечения.
Напряжения в точке С, принадлежащей
этой кромке, равно нулю. Наибольшее
сжимающее напряжение возникнет в точке
D правой кромки сечения.
Вычислим эти напряжения:
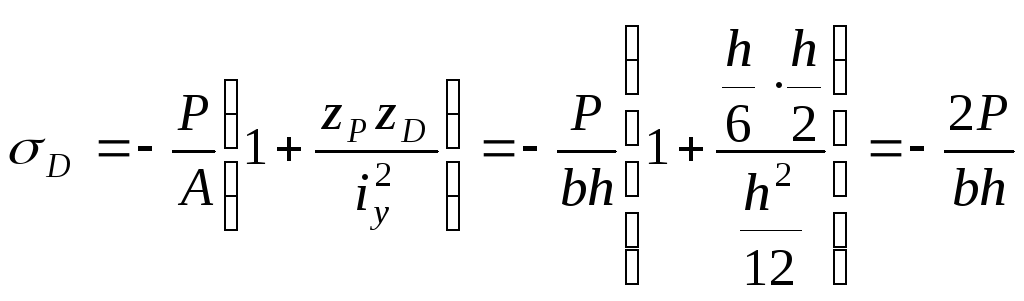 .
.
(б)
На рис.12.21,г приведена
эпюра распределения нормальных напряжений
по площади сечения. Максимальные по
величине напряжения возникают в точке
Dсечения.
3.
Сравнивая напряжения