Силы растяжения и сила тяжести

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Основные законы Динамики. Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах.
Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос: | ||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||
Источник
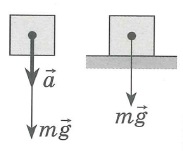
В данном параграфе мы напомним Вам о силе тяжести, центростримительном ускорение и весе тела
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести
Fт=GMm/R2
где М — масса Земли; R — радиус Земли.
Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле Fт=GMm/R2 модуль ускорения свободного падения g находят по формуле
g=Fт/m=GM/R2.
Из формулы (2.29) следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде
Fт=mg
В § 5 было отмечено, что поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. Из формулы Fт=GMm/R2 видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.
Сила тяжести действует на все тела, находящиеся в поле тяготения Земли, однако не все тела падают на Землю. Это объясняется тем, что движению многих тел препятствуют другие тела, например опоры, нити подвеса и т. п. Тела, ограничивающие движение других тел, называют связями. Под действием силы тяжести связи деформируются и сила реакции деформированной связи по третьему закону Ньютона уравновешивает силу тяжести.
На ускорение свободного падения влияет вращение Земли. Это влияние объясняется так. Системы отсчета, связанные с поверхностью Земли (кроме двух, связанных с полюсами Земли), не являются, строго говоря, инерциальными системами отсчета — Земля вращается вокруг своей оси, а вместе с ней движутся по окружностям с центростремительным ускорением и такие системы отсчета. Эта неинерциальность систем отсчета проявляется, в частности, в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения.
Измерения, проведенные на разных широтах, показали, что числовые значения ускорения свободного падения мало отличаются друг от друга. Поэтому при не очень точных расчетах можно пренебречь неинерциальностью систем отсчета, связанных с поверхностью Земли, а также отличием формы Земли от сферической, и считать, что ускорение свободного падения в любом месте Земли одинаково и равно 9,8 м/с2.
Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле
g=GM/(R+h) 2.
Установлено, что на высоте 300 км над поверхностью Земли ускорение свободного падения меньше, чем у поверхности Земли, на 1 м/с2.
Следовательно, вблизи Земли (до высот нескольких километров) сила тяжести практически не изменяется, а потому свободное падение тел вблизи Земли является движением равноускоренным.
Вес тела. Невесомость и перегрузки
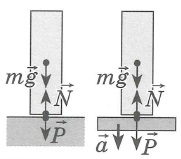
Силу, в которой вследствие притяжения к Земле тело действует на свою опору или подвес, называют весом тела. В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес — это упругая сила, приложенная к опоре или подвесу (т. е. к связи).
Наблюдения показывают, что вес тела Р, определяемый на пружинных весах, равен действующей на тело силе тяжести Fт только в том случае, если весы с телом относительно Земли покоятся или движутся равномерно и прямолинейно; В этом случае
Р=Fт=mg.
Если же тело движется ускоренно, то его вес зависит от значения этого ускорения и от его направления относительно направления ускорения свободного падения.
Когда тело подвешено на пружинных весах, на него действуют две силы: сила тяжести Fт=mg и сила упругости Fyп пружины. Если при этом тело движется по вертикали вверх или вниз относительно направления ускорения свободного падения, значит векторная сумма сил Fт и Fуп дает равнодействующую, вызывающую ускорение тела, т. е.
Fт + Fуп=mа.
Согласно приведенному выше определению понятия «вес», можно написать, что Р=-Fyп. Из формулы: Fт + Fуп=mа. с учетом того, что Fт=mg, следует, что mg-mа=-Fyп. Следовательно, Р=m(g-а).
Силы Fт и Fуп направлены по одной вертикальной прямой. Поэтому если ускорение тела а направлено вниз (т.е. совпадает по направлению с ускорением свободного падения g), то по модулю
P=m(g-a)
Если же ускорение тела направлено вверх (т. е. противоположно направлению ускорения свободного падения), то
Р = m[g — (- а)] = m(g+а).
Следовательно, вес тела, ускорение которого совпадает по направлению с ускорением свободного падения, меньше веса покоящегося тела, а вес тела, ускорение которого противоположно направлению ускорения свободного падения, больше веса покоящегося тела. Увеличение веса тела, вызванное его ускоренным движением, называют перегрузкой.
При свободном падении a=g. Из формулы:P=m(g-a)
следует, что в таком случае Р=0, т. е. вес отсутствует. Следовательно, если тела движутся только под действием силы тяжести (т. е. свободно падают), они находятся в состоянии невесомости. Характерным признаком этого состояния является отсутствие у свободно падающих тел деформаций и внутренних напряжений, которые вызываются у покоящихся тел силой тяжести. Причина невесомости тел заключается в том, что сила тяжести сообщает свободно падающему телу и его опоре (или подвесу) одинаковые ускорения.
Источник
Си́ла тя́жести — сила, действующая на любое физическое тело вблизи поверхности астрономического объекта (планеты, звезды) и складывающаяся из силы гравитационного притяжения этого объекта и центробежной силы инерции, вызванной его суточным вращением[1][2].
Прочие приложенные к телу силы — такие как силы Кориолиса[3][4][5] при движении тела по поверхности планеты и Архимеда при наличии атмосферы или жидкости — в силу тяжести не включаются.
В большинстве практических случаев анализируется сила тяжести вблизи Земли. Для неё величина центробежной силы составляет доли процента от величины гравитационной и иногда игнорируется.
Сила тяжести , действующая на материальную точку массой , вычисляется по формуле[6]
,
где — ускорение свободного падения[7]. Сила тяжести является консервативной[8]. Она сообщает любому телу, независимо от его массы, ускорение [6]. Значение диктуется параметрами (массой , размерами, скоростью вращения ) планеты или звезды и координатами на её поверхности.
Если в пределах протяжённого тела поле тяжести приблизительно однородно, то равнодействующая сил тяжести, действующих на элементы этого тела, приложена к центру масс тела[9].
В нерусскоязычной литературе термин «сила тяжести» не вводится — вместо этого говорят о фундаментальном гравитационном взаимодействии, при необходимости делая уточнение о центробежной добавке.
Cила тяжести mg складывается из гравитационного притяжения планеты GMm/r2 и центробежной силы инерции mω2a.
История[править | править код]
Личности, внёсшие исторический вклад в развитие представлений о силе тяжести:
Аристотель объяснял силу тяжести движением тяжёлых физических стихий (земля, вода) к своему естественному месту (центру Вселенной внутри Земли), причём скорость тем больше, чем ближе тяжёлое тело к нему[10].
Архимед рассмотрел вопрос о центре тяжести параллелограмма, треугольника, трапеции и параболического сегмента. В сочинении «О плавающих телах» Архимед доказал закон гидростатики, носящий его имя[10].
Иордан Неморарий в сочинении «О тяжестях» при рассмотрении грузов на наклонной плоскости разлагал их силы тяжести на нормальную и параллельную наклонной плоскости составляющие, был близок к определению статического момента[11].
Стевин экспериментально определил, что тела разных масс падают с одинаковым ускорением, установил теоремы о давлении жидкости в сосудах (давление зависит только от глубины и не зависит от величины, формы и объёма сосуда) и о равновесии грузов на наклонной плоскости (на наклонных плоскостях равной высоты силы, действующие со стороны уравновешивающихся грузов вдоль наклонных плоскостей, обратно пропорциональны длинам этих плоскостей). Доказал теорему, согласно которой в случае равновесия центр тяжести однородного плавающего тела должен находиться выше центра тяжести вытесненной жидкости[12].
Галилей экспериментально исследовал законы падения тел (ускорение не зависит от веса тела), колебаний маятников (период колебаний не зависит от веса маятника) и движения по наклонной плоскости[13].
Гюйгенс создал классическую теорию движения маятника, оказавшую значительное влияние на теорию тяготения[13].
Декарт разработал кинетическую теорию тяготения, объяснявшую силу тяжести взаимодействием тел с небесным флюидом, выдвинул гипотезу о зависимости силы тяжести от расстояния между тяжёлым телом и центром Земли[13].
Ньютон из равенства ускорений падающих тел и второго закона Ньютона сделал вывод о пропорциональности силы тяжести массам тел и установил, что сила тяжести является одним из проявлений силы всемирного тяготения[14][15]. Для проверки этой идеи он сравнил ускорение свободного падения тел у поверхности Земли с ускорением Луны на орбите, по которой она движется относительно Земли[16].
Эйнштейн объяснил факт равенства ускорений падающих тел независимо от их массы (эквивалентность инертной и тяжёлой массы)
как следствие принципа эквивалентности равномерно ускоренной системы отсчёта и системы отсчёта, находящейся в гравитационном поле[17].
Сила тяжести в различных ситуациях[править | править код]
Сферически симметричный небесный объект[править | править код]
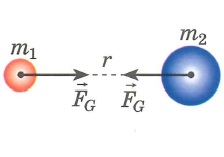
В соответствии с законом всемирного тяготения, модуль силы гравитационного притяжения , действующей на материальную точку на поверхности астрономического объекта со сферически симметричным распределением массы по объёму, определяется соотношением
,
где — гравитационная постоянная, равная 6,67384(80)·10−11м3·с−2·кг−1, — радиус астрономического тела, — его масса, — масса материальной точки. Сила гравитационного притяжения направлена к центру тела.
Модуль центробежной силы инерции , действующей на материальную точку, задаётся формулой
,
где — расстояние между частицей и осью вращения рассматриваемого астрономического объекта, — угловая скорость его вращения. Центробежная сила инерции перпендикулярна оси и направлена от неё.
Сита тяжести вычисляется по теореме косинусов:
.
Здесь — «широта» места на планете или звезде, для которого производится расчёт.
Планеты Солнечной системы в шаровом приближении[править | править код]
Приближённо, Солнце и планеты Солнечной системы можно рассматривать как сферически симметричные астрономические объекты, а при грубом вычислении брать широту = 450 («посредине»). Сравнение силы тяжести, оцененной в таком приближении, на поверхностях[18] ряда планет представлено в таблице. За единицу принята сила тяжести на Земле[19].
| Земля | 1,00 | Солнце | 27,85 |
| Луна | 0,165 | Меркурий | 0,375—0,381 |
| Венера | 0,906 | Марс | 0,394 |
| Юпитер | 2,442 | Сатурн | 1,065 |
| Уран | 0,903 | Нептун | 1,131 |
В условиях Земли и других планет, поправки, вносимые общей теорией относительности в закон всемирного тяготения, крайне малы (модуль гравитационного потенциала на поверхности Земли, равный половине квадрата второй космической скорости , крайне мал по сравнению с квадратом скорости света: )[20].
Планета Земля с учётом особенностей её формы[править | править код]
Форма Земли (геоид) отличается от строго шарообразной и близка к сплюснутому эллипсоиду.
Соответственно, в более точном, чем шаровое, приближении, сила гравитационного притяжения, действующая на материальную точку массой , определяется выражением
,
где — элемент массы Земли ( — плотность), и — радиус-векторы точки измерения и элемента массы Земли соответственно. Интегрирование выполняется по всему объёму Земли.
В векторной форме выражение для центробежной силы инерции можно записать в виде
,
где — вектор, перпендикулярный оси вращения и проведённый от неё к точке измерения.
Сила тяжести является суммой и :
Сила тяжести вблизи поверхности Земли зависит от широты места и высоты над уровнем моря. Широтное изменение связано как с отклонением формы Земли от шарообразной, так и с наличием центробежной силы. Приблизительное выражение для абсолютной величины силы тяжести в системе СИ имеет вид[7]
Угол между силой тяжести и силой гравитационного притяжения к Земле равен[21]:
.
Он изменяется в пределах от нуля (на экваторе, где и на полюсах, где ) до рад или (на широте ).
Дополнительно, можно учесть эффект притяжения Луны и Солнца (искусственно введя временные изменения гравитационного поля Земли, то есть добавки к ), несмотря на его малость[22][23][24].
Статика и динамика тела в поле тяжести Земли[править | править код]
Устойчивость тела в поле силы тяжести[править | править код]
Для тела в поле силы тяжести, опирающегося на одну точку (например при подвешивании тела за одну точку или помещении шара на плоскость) для устойчивого равновесия необходимо, чтобы центр тяжести тела занимал наинизшее положение по сравнению со всеми возможными соседними положениями[25].
Для тела в поле силы тяжести, опирающегося на несколько точек (например, стол) или на целую площадку (например, ящик на горизонтальной плоскости) для устойчивого равновесия необходимо, чтобы вертикаль, проведённая через центр тяжести, проходила внутри площади опоры тела. Площадью опоры тела называется контур, соединяющий точки опоры или внутри площадки, на которое опирается тело[25].
Потенциальная энергия поднятого над Землей тела[править | править код]
Потенциальная энергия поднятого над Землей тела может быть найдена как взятая с обратным знаком работа силы тяжести при перемещении тела с поверхности Земли в данное положение. Если пренебречь центробежной силой и считать Землю шаром, эта энергия равна:
,
где — гравитационная постоянная, — масса Земли, — масса тела, — радиус Земли, — расстояние от тела до центра Земли.
При удалении тела от поверхности Земли не небольшие, по сравнению с , расстояния поле тяготения можно считать однородным, а ускорение свободного падения постоянным. В этом случае при подъёме тела массой на высоту от поверхности Земли сила тяжести совершает работу . Поэтому потенциальная энергия тела составляет , если за нуль энергии взята энергия на поверхности планеты. Тело, находящееся на глубине от поверхности Земли, обладает отрицательным значением потенциальной энергии [26].
Движение тел под действием силы тяжести Земли[править | править код]
В случае, когда модуль перемещения тела много меньше расстояния до центра Земли, можно считать силу тяжести постоянной, а движение тела равноускоренным. Если начальная скорость тела отлична от нуля и её вектор направлен не по вертикали, то под действием силы тяжести тело движется по параболической траектории.
При бросании тела с некоторой высоты параллельно поверхности Земли дальность полёта увеличивается с ростом начальной скорости. При больших значениях начальной скорости для вычисления траектории тела необходимо учитывать шарообразную форму Земли и изменение направления силы тяжести в разных точках траектории.
При некотором значении скорости, называемом первой космической скоростью, тело, брошенное по касательной к поверхности Земли, под действием силы тяжести при отсутствии сопротивления со стороны атмосферы может двигаться вокруг Земли по окружности, не падая на Землю. При скорости, превышающую вторую космическую скорость, тело уходит от поверхности Земли в бесконечность по гиперболической траектории. При скоростях, промежуточных между первой и второй космическими, тело движется вокруг Земли по эллиптической траектории[27].
Глобальная роль силы тяжести в природе[править | править код]
В эволюции строения планет и звёзд[править | править код]
Сила тяжести играет огромную роль в процессах эволюции звёзд. Для звёзд, находящихся на этапе главной последовательности своей эволюции, сила тяжести является одним из важных факторов, обеспечивающих условия, необходимые для термоядерного синтеза. На заключительных этапах эволюции звёзд, в процессе их коллапса, благодаря силе тяжести, не скомпенсированной силами внутреннего давления, звёзды превращаются в нейтронные звёзды или чёрные дыры.
Сила тяжести важна для формирования внутренней структуры планет, включая Землю, и тектонической эволюции их поверхностей[28]. Чем больше сила тяжести, тем большая масса метеоритного материала выпадает на единицу поверхности планеты[29]. За время существования Земли её масса существенно увеличилась благодаря силе тяжести: ежегодно на Землю оседает 30-40 млн. тонн метеоритного вещества, в основном в виде пыли, что значительно превышает рассеяние лёгких компонентов верхней атмосферы Земли в космосе[30].
Потенциальная энергия перемещаемых тектоническими процессами масс горных пород тратится на перемещение продуктов разрушения горных пород с повышенных участков поверхности на нижерасположенные[31].
В создании условий для жизни на Земле[править | править код]
Сила тяжести чрезвычайно значима для жизни на Земле[32]. Только благодаря ей у Земли есть атмосфера. Вследствие силы тяжести, действующей на воздух, существует атмосферное давление[33].
Без потенциальной энергии силы тяжести, непрерывно переходящей в кинетическую, круговорот вещества и энергии на Земле был бы невозможен[34].
При испарении воды с поверхности Земли энергия солнечной радиации трансформируется в потенциальную энергию водяного пара в атмосфере. Затем при выпадении атмосферных осадков на сушу она переходит при стоке в кинетическую энергию и совершает эрозионную работу в процессе переноса денудационного материала всей суши и делает возможным жизнь органического мира на Земле[35].
У всех живых организмов с нервной системой есть рецепторы, определяющие величину и направление силы тяжести и служащие для ориентировки в пространстве. У позвоночных организмов, в том числе человека, величину и направление силы тяжести определяет вестибулярный аппарат[36].
Наличие силы тяжести привело к возникновению у всех многоклеточных наземных организмов прочных скелетов, необходимых для её преодоления. У водных живых организмов силу тяжести уравновешивает гидростатическая сила[37].
Роль силы тяжести в процессах жизнедеятельности организмов изучает гравитационная биология[38].
Применение силы тяжести Земли в технике[править | править код]
Сила тяжести и принцип эквивалентности инертной и гравитационной массы используются для определения масс предметов путём их взвешивания на весах. Сила тяжести используется при отстойной сепарации газовых и жидких смесей, в процессах гравитационного обогащения полезных ископаемых, в некоторых типах часов, в отвесах и противовесах, машине Атвуда, машине Обербека и жидкостных барометрах. Сила тяжести используется на железнодорожном транспорте для скатывания вагонов с уклона на сортировочных горках, на заводах строительных изделий для транспортировки материалов в спускных лотках и спускных трубах.[39]
Точные измерения силы тяжести и её градиента (гравиметрия) используются при исследовании внутреннего строения Земли и при гравиразведке различных полезных ископаемых[40].
Методы измерения силы тяжести[править | править код]
Основной источник: [41]
Силу тяжести измеряют динамическими и статическими методами. Динамические методы используют наблюдение за движением тела под действием силы тяжести и измеряют время перехода тела из одного заранее определённого положения в другое. Они используют: колебания маятника, свободное падение тела, колебания струны с грузом. Статические методы используют наблюдение за изменением положения равновесия тела под действием силы тяжести и некоторой уравновешивающей её силы и измеряют линейное или угловое смещение тела.
Измерения силы тяжести бывают абсолютными и относительными. Абсолютные измерения определяют полное значение силы тяжести в заданной точке. Относительные измерения определяют разность силы тяжести в заданной точке и некоторого другого, заранее известного значения. Приборы, предназначенные для относительных измерений силы тяжести, называются гравиметрами.
Динамические методы определения силы тяжести могут быть как относительными, так и абсолютными, статические — только относительными.
См. также[править | править код]
- Вес
- Ускорение свободного падения
- Гравиметрия (геодезия)
Примечания[править | править код]
- ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 372. — 560 с. — ISBN 5-9221-0225-7.
- ↑ Тарг С. М. Сила тяжести // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 496. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Тарасов, 2012, с. 200, 270.
- ↑ Савельев, 1987, с. 128.
- ↑ Бутенин, 1971, с. 253-259.
- ↑ 1 2 Савельев, 1987, с. 70.
- ↑ 1 2 Ускорение свободного падения // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. — С. 245—246. — 760 с. — ISBN 5-85270-101-7.
- ↑ Савельев, 1987, с. 82-83.
- ↑ Савельев, 1987, с. 156.
- ↑ 1 2 Зубов В. П. Физические идеи древности // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 38, 54-55;
- ↑ Зубов В. П. Физические идеи средневековья // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 114;
- ↑ Зубов В. П. Физические идеи ренессанса // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 151;
- ↑ 1 2 3 Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред.
Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177; - ↑ Ньютон, 1989, с. 7.
- ↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 189-191;
- ↑ Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 323
- ↑ Иваненко Д. Д. Основные идеи общей теории относительности // отв. ред. Григорьян А. Т., Полак Л. С.
Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 300; - ↑ У газовых гигантов «поверхность» понимается как область высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105Па).
- ↑ Данные взяты из статьи Википедии Ускорение свободного падения
- ↑ Грищук Л. П., Зельдович Я. Б. Тяготение // Физика космоса. Маленькая энциклопедия. — М., Советская энциклопедия, 1986. — С. 676
- ↑ Савельев, 1987, с. 122.
- ↑ Миронов, 1980, с. 49.
- ↑ Максимальное изменение силы тяжести, обусловленное притяжением Луны, составляет примерно м/с2, Солнца м/с2
- ↑ Миронов, 1980, с. 71.
- ↑ 1 2 Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика, теплота, молекулярная физика. — М., Наука, 1975. — Тираж 350 000 экз. — С. 189-190
- ↑ Кабардин О.Ф., Орлов В.А., Пономарева А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 151 — 152
- ↑ Жирнов Н. И. Классическая механика. — М., Просвещение, 1980. — Тираж 28000 экз. — с. 121
- ↑ Криволуцкий, 1985, с. 208.
- ↑ Криволуцкий, 1985, с. 77.
- ↑ Криволуцкий, 1985, с. 48, 237-238.
- ↑ Криволуцкий, 1985, с. 70, 234.
- ↑ Зельманов А. Л. Многообразие материального мира и проблема бесконечности Вселенной // Бесконечность и Вселенная. — М., Мысль, 1969. — Тираж 12000 экз. — С. 283
- ↑ Хромов С. П., Петросянц М. А. Метеорология и климатология. — М., МГУ, 2006. — ISBN 5-211-05207-2. — C. 67
- ↑ Криволуцкий, 1985, с. 289.
- ↑ Криволуцкий, 1985, с. 307.
- ↑ Юрий Фролов. https://www.nkj.ru/archive/articles/21172/ Наш гравитационный компас] (рус.) // Наука и жизнь. — 2012. — № 10.
- ↑ П. Кемп, К. Армс Введение в биологию. — М.: Мир, 1988. — ISBN 5-03-001286-9. — Тираж 125000 экз. — С. 75
- ↑ Лозовская Е. Жизнь с гравитацией и без нее (рус.) // Наука и жизнь. — 2004. — № 9.
- ↑ Фиделев А. С. Подъемно-транспортные машины и механизмы. — Киев, Будивельник, 1967. — 187-188
- ↑ Миронов, 1980, с. 1-543.
- ↑ Миронов, 1980, с. 94-262.
Литература[править | править код]
- Ньютон И. Математические начала натуральной философии. — М.: Наука, 1989. — 688 с. — ISBN 5-02-000747-1.
- Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика. — М.: Наука, 1987. — 688 с.
- Криволуцкий А. Е. Голубая планета. Земля среди планет. Географический аспект. — М.: Мысль, 1985. — 335 с.
- Миронов В. С. Курс гравиразведки. — Л.: Недра, 1980. — 543 с.
- Тарасов В. Н., Бояркина И. В., Коваленко М. В., Федорченко Н. П., Фисенко Н. И. Теоретическая механика. — М.: ТрансЛит, 2012. — 560 с.
- Бутенин Н. В. Введение в аналитическую механику. — М.: Наука, 1971. — 264 с. — 25 000 экз.
Источник