Сила растяжения проводника с током
На основе магнитных явлениях построено действие электротехнических устройств. Все современные электромоторы, генераторы и множество других электромеханических приборов работают по принципу взаимодействия электрического тока с окружающими его магнитными полями. Эти взаимодействия описывает знаменитый закон Ампера, названный так в честь своего первооткрывателя.
Влияние электричества на поведение магнитной стрелки впервые обнаружил Х. К. Эрстед. Он заметил, что вопреки ожиданию, магнитное поле не параллельно вектору тока, а перпендикулярно ему. Развивая выводы Эрстеда, и продолжая исследования в этом направлении, Мари Ампер установил [1], что электричество взаимодействует не только с магнитами, но и между собой. Заслуга Ампера в том, что он теоретически обосновал взаимное влияние токов и предоставил формулу, позволяющую вычислять силы этого взаимодействия.
Определение и формула
Экспериментальным путём Ампер установил, что между двумя параллельными проводниками, подключенными к постоянному току, действует притяжение (однонаправленные токи) либо отталкивание (если направления противоположные). Эти силы взаимодействия определяются параметрами токов (прямо пропорциональная зависимость), и расстоянием между проводниками (обратно пропорциональная зависимость).
Расчёт амперовой силы на единицу длины проводника осуществляется по формуле:

где F – сила, I1, I2 – величина тока в проводниках, а μ – магнитная проницаемость среды, окружающей проводники (см. рис. 1).
Природой взаимодействия является магнитное поле, образованное перемещаемыми по проводникам электрическими зарядами. Под влиянием магнитного поля на электрические заряды возникает сила магнитной индукции, которую обозначают символом B.
Линии, в каждой точке которых касательные к ним совпадают с направлением соответствующих векторов магнитной индукции, получили название линий электромагнитной индукции. Применяя мнемоническое правило буравчика, можно определить ориентацию в пространстве линий магнитной индукции. То есть, при ввинчивании буравчика в сторону, куда направлен вектор электрического тока, движение концов его рукоятки укажет направление векторов индукции.
Из сказанного выше следует, что в проводниках, с одинаково ориентированными токами, направления векторов магнитной индукции совпадают, а значит, векторы сил направлены навстречу друг к другу, что и вызывает притяжение.
 Рис. 1. Взаимодействие параллельных проводников
Рис. 1. Взаимодействие параллельных проводников
Подобным образом проводники взаимодействуют не только между собой, но и с магнитными полями любой природы. Если такой проводник окажется в магнитном поле, то на элемент, расположенный в зоне действия магнита, будет действовать сила, которую именуют Амперовой:
![]()
Для вычисления модуля этой силы пользуются формулой: dF = IBlsinα , где α — угол, образованный векторами индукции и ориентацией тока.
Рассмотренную нами зависимость описывает закон Ампера, формулировка которого понятна из рисунка 2.
 Рис. 2. Формулировка закона Ампера
Рис. 2. Формулировка закона Ампера
Не трудно сообразить, что когда α = 900, то sinα = 1. В этом случае величина F приобретает максимальное значение: F = B*L*I, где L– длина проводника, оказавшегося под действием магнитного поля.
Таким образом, из закона Ампера вытекает:
- проводник с током реагирует на магнитные поля.
- действующая сила находится в прямо пропорциональной зависимости от параметров тока, величины магнитной индукции и размеров проводника.
Обратите внимание, что на данном рисунке 3 проводник расположен под углом 90º к линиям магнитной индукции, что вызывает максимальное действие магнитных сил.
 Рис. 3. Проводник в магнитном поле
Рис. 3. Проводник в магнитном поле
Направление силы Ампера
Принимая к сведению то, что сила – векторная величина, определим её направление. Рассмотрим случай, когда проводник с током расположен между двумя полюсами магнитов под прямым углом к линиям магнитной индукции.
Выше мы установили, что согласно закону Ампера, действующая на данный проводник сила, равна: F = B*L*I. Направление вектора рассматриваемой силы определяется по результатам векторного произведения:

Если полюса магнита статичны (неподвижны), то векторное произведение будет зависеть только от параметров электричества, в частности, от того, в какую сторону оно течёт.
Направление силы Ампера определяют по известному правилу левой руки: ладонь располагают навстречу магнитным линиям, а пальцы размещают вдоль проводника, в сторону устремления тока. На ориентацию силы Ампера указывает большой палец, образующий прямой угол с ладонью (см. рис. 4).
 Рис. 4. Интерпретация правила
Рис. 4. Интерпретация правила
Измените мысленно направление электрического тока, и вы увидите, что направление вектора Амперовой силы изменится на противоположное. Модуль вектора имеет прямо пропорциональную зависимость от всех сомножителей, но на практике эту величину удобно регулировать путём изменения параметров в электрической цепи (например, для регулировки мощности электродвигателя).
Применение
Закон Ампера, а точнее следствия, вытекающие из него, используются в каждом электромеханическом устройстве, где необходимо вызвать движение рабочих элементов. Самым распространённым механизмом, работа которого базируется на законе Ампера, является электродвигатель.
Применение электромоторов настолько широкое, что его можно увидеть практически во всех сферах человеческой деятельности:
- на производстве, в качестве приводов станков и различного оборудования;
- в бытовой сфере (бытовая электротехника);
- в электроинструментах;
- на транспорте;
- в устройствах автоматики, в офисной технике и во многих других сферах.
Из закона Ампера вытекает возможность получения электротока путём перемещения проводников, находящихся в магнитном поле. На данном принципе построены все генераторы электрического тока. Благодаря этой уникальной возможности, у нас появился доступ к использованию электроэнергии для различных потребностей.
Мы буквально окружены проявлением закона Ампера. Например, просмотр телепередачи сопровождается звуком, который транслируется через динамики. Но диффузор динамика приводит в движение сила Ампера. Мы разговариваем по телефону – там тоже есть динамик и микрофон. Принцип действия современных микрофонов также основан на законе Ампера.
Вход в помещение через автоматическую раздвижную дверь, поднятие на лифте, поездка в троллейбусе, трамвае, запуск двигателя автомобиля – всё это было бы невозможным, если бы не существовало взаимодействия электрического тока с силами магнитной индукции.
Ампер открыл перед человечеством такие возможности, без которых развитие научно-технического прогресса было бы невозможным. Влияние этого закона в электротехнике сравнимо с законами Ньютона, которые в своё время совершили революцию в механике. В этом огромная заслуга учёного-физика Мари Ампера, труды которого увенчались открытием в 1820 г. знаменитого закона.
Источник
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Электродинамика
Магнитное поле
1.16. Магнитное взаимодействие токов
Магнитные явления были известны еще в древнем мире. Компас был изобретен более 4500 лет тому назад. В Европе он появился приблизительно в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле.
Первыми экспериментами (проведены в 1820 г.), показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Х. Эрстеда. Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся ее повернуть. В том же году французский физик А. Ампер наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов.
По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля.
Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).
Ученые XIX века пытались создать теорию магнитного поля по аналогии с электростатикой, вводя в рассмотрение так называемые магнитные заряды двух знаков (например, северный N и южный S полюса магнитной стрелки). Однако опыт показывает, что изолированных магнитных зарядов не существует.
Магнитное поле токов принципиально отличается от электрического поля. Магнитное поле, в отличие от электрического, оказывает силовое действие только на движущиеся заряды (токи).
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности электрического поля. Такой характеристикой является вектор магнитной индукции который определяет силы, действующие на токи или движущиеся заряды в магнитном поле.
За положительное направление вектора принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно ориентирующийся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора Такое исследование позволяет наглядно представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор направлен по касательной. Пример линий магнитной индукции полей постоянного магнита и катушки с током приведен на рис. 1.16.1.
| Рисунок 1.16.1. Линии магнитной индукции полей постоянного магнита и катушки с током. Индикаторные магнитные стрелки ориентируются по направлению касательных к линиям индукции |
Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.
Для того, чтобы количественно описать магнитное поле, нужно указать способ определения не только направления вектора но и его модуля. Проще всего это сделать, внося в исследуемое магнитное поле проводник с током и измеряя силу, действующую на отдельный прямолинейный участок этого проводника. Этот участок проводника должен иметь длину Δl, достаточно малую по сравнению с размерами областей неоднородности магнитного поля. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции:
Эта сила называется силой Ампера. Она достигает максимального по модулю значения Fmax, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции. Модуль вектора
определяется следующим образом:
Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока I в проводнике и его длине Δl:
В общем случае сила Ампера выражается соотношением:
Это соотношение принято называть законом Ампера.
В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл).
Тесла – очень крупная единица. Магнитное поле Земли приблизительно равно 0,5·10–4 Тл. Большой лабораторный электромагнит может создать поле не более 5 Тл.
Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (рис. 1.16.2).
| Рисунок 1.16.2. Правило левой руки и правило буравчика |
Если угол α между направлениями вектора и тока в проводнике отличен от 90°, то для определения направления силы Ампера более удобно пользоваться правилом буравчика: воображаемый буравчик располагается перпендикулярно плоскости, содержащей вектор и проводник с током, затем его рукоятка поворачивается от направления тока к направлению вектора Поступательное перемещение буравчика будет показывать направление силы Ампера (рис. 1.16.2). Правило буравчика часто называют правилом правого винта.
Одним из важных примеров магнитного взаимодействия является взаимодействие параллельных токов. Закономерности этого явления были экспериментально установлены Ампером. Если по двум параллельным проводникам электрические токи текут в одну и ту же сторону, то наблюдается взаимное притяжение проводников. В случае, когда токи текут в противоположных направлениях, проводники отталкиваются.
Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот.
Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I1 и I2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:
В Международной системе единиц СИ коэффициент пропорциональности k принято записывать в виде:
где μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно
μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2.
Формула, выражающая закон магнитного взаимодействия параллельных токов, принимает вид:
Отсюда нетрудно получить выражение для индукции магнитного поля каждого из прямолинейных проводников. Магнитное поле прямолинейного проводника с током должно обладать осевой симметрией и, следовательно, замкнутые линии магнитной индукции могут быть только концентрическими окружностями, располагающимися в плоскостях, перпендикулярных проводнику. Это означает, что векторы и магнитной индукции параллельных токов I1 и I2 лежат в плоскости, перпендикулярной обоим токам. Поэтому при вычислении сил Ампера, действующих на проводники с током, в законе Ампера нужно положить sin α = 1. Из закона магнитного взаимодействия параллельных токов следует, что модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением
Для того, чтобы при магнитном взаимодействии параллельные токи притягивались, а антипараллельные отталкивались, линии магнитной индукции поля прямолинейного проводника должны быть направлены по часовой стрелке, если смотреть вдоль проводника по направлению тока. Для определения направления вектора магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора если при вращении буравчик перемещается в направлении тока (рис. 1.16.3).
| Рисунок 1.16.3. Магнитное поле прямолинейного проводника с током |
| Рисунок 1.16.4. Магнитное взаимодействие параллельных и антипараллельных токов |
Рис. 1.16.4 поясняет закон взаимодействия параллельных токов.
Магнитное взаимодействие параллельных проводников с током используется в Международной системе единиц (СИ) для определения единицы силы тока – ампера:
Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, равную 2·10–7 Н на каждый метр длины.
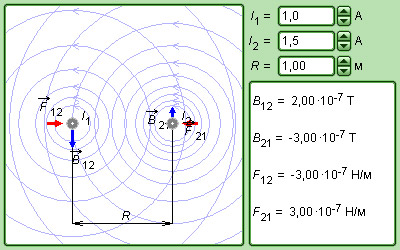 |
Модель. |
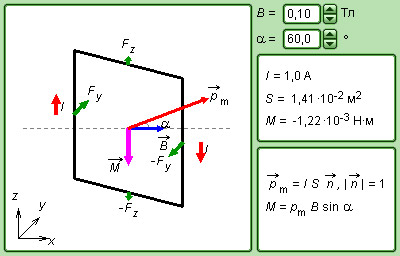 |
Модель. |
Источник
Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
Ампер первым установил, что проводники, по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются).
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера. Ее обозначения: ( overrightarrow{F} ),( overrightarrow{F}_{A} ).
Сила (( overrightarrow{F} )), которая действует на прямолинейный проводник с током (I), всегда перпендикулярна проводнику и направлению вектора магнитной индукции (( overrightarrow{B} )). В том случае, если прямолинейный проводник расположен параллельно вдоль направления линий магнитного поля, поле не действует.
Конкретное направление силы Ампера можно найти с помощью правила левой руки. Левую руку надо расположить так, чтобы линии поля входили в ладонь, четыре пальца были направлены по току, тогда отогнутый на 90 градусов большой палец укажет направление силы Ампера.
Еще Ампер установил, что два параллельных проводника с током притягиваются, если токи имеют одинаковые направления и отталкиваются, если токи текут в противоположные стороны. Это просто объяснить, если представить, что один проводник создает магнитное поле, а другой проводник в него помещен и это поле действует на него. Можно использовать правило левой руки и выяснить, как направлена сила.
Закон Ампера
Сила Ампера – сила, действующая на проводник тока, находящийся в магнитном поле и равная произведению силы тока в проводнике, модуля вектора индукции магнитного поля, длины проводника и синуса угла между вектором магнитного поля и направлением тока в проводнике.
Для прямолинейного проводника сила Ампера имеет вид:
[ large{overrightarrow{F}_{A}} = I cdot overrightarrow{B} cdot overrightarrow{l} cdot sin(α) ]
где: ( I ) — сила тока, которая течет в проводнике, ( overrightarrow{B} ) — вектор индукции магнитного поля, в которое проводник помещен, ( overrightarrow{l} ) — длина проводника в поле, направление задано направлением тока, ( alpha ) — угол между векторами ( overrightarrow{l }и overrightarrow{B} ).
Этой формулой можно пользоваться:
- если длина проводника такая, что индукция во всех точках проводника может считаться одинаковой;
- если магнитное поле однородное (тогда длина проводника может быть любой, но при этом проводник целиком должен находиться в поле).
Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом:
[ large{doverrightarrow{F}_{A}} = I cdot overrightarrow{B} cdot doverrightarrow{l} cdot sin(α) ]
Значение закона Ампера
На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную ( 2cdot {10}^{-7}Н ) на каждый метр длины.
Ток в один ампер – это такой ток, при котором два однородных параллельных проводника, расположенные в вакууме на расстоянии один метр друг от друга взаимодействуют с силой ( 2cdot {10}^{-7} ) Ньютона.
Закон взаимодействия токов – два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.
Источник
В магнитном поле, направленном вертикально вниз на двух невесомых нитях горизонтально подвешен проводник с током силы I=2А. Масса проводника ( m=10^{-2} ) кг, длина l=0,4м. Индукция магнитного поля равна 0,25Тл. Определите величину угла, на который отклонятся нити, на которых висит проводник с током. Проводник весь находится в поле.
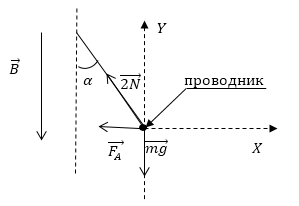
Рис. 2
Проводник расположен перпендикулярно плоскости рисунка (ток направлен от нас). Запишем условие равновесия для проводника:
[ overrightarrow{F_A}+overrightarrow{mg}+2overrightarrow{N}=0 left(1.1right), ]
где ( overrightarrow{F_A} )- сила Ампера, ( overrightarrow{mg} ) — сила тяжести, ( overrightarrow{N} ) — сила реакции нити.
Проектируем (1.1) на оси:
[ X: -F_A-2Nsinalpha =0 left(1.2right). ]
[ Y: -mg+2Ncosalpha =0 left(1.3right). ]
Разделим (1.2) на (1.3), получим:
[ frac{F_A}{mg}=tgalpha left(1.4right). ]
Модуль силы Ампера для прямолинейного проводника с током, который подвешен в поле с током, причем ( overrightarrow{B}bot overrightarrow{l} )равен:
[ F_A=IBl left(1.5right). ]
Перепишем (1.4) с учетом (1.5), получим:
[ frac{IBl}{mg}=tgalpha left(1.6right). ]
Подставим исходные данные, проведём вычисления:
[ tgalpha =frac{2cdot 0,25cdot 0,4}{10^{-2}cdot 9,8}approx 2 ]
( alpha approx 64{}^circ ).
Уровень9 класс ПредметФизика СложностьПростая
Один проводник с током имеет форму квадрата, по нему утечет ток I. В одной плоскости с рамкой лежит бесконечно длинный прямой проводник с таким же током. Расположение проводников задано на рис.3. Найдите, какова сила, действующая на рамку, если расстояние между одной из сторон рамки и проводом равно длине стороны квадрата.
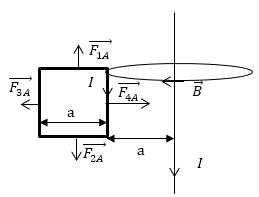
Рис. 3
Решение:
Магнитное поле создается бесконечно длинным проводником с током. Модуль индукции этого поля нам известен его можно записать как:
[ Bleft(rright)=frac{{mu }_0}{2pi }frac{I}{r}left(2.2right), ]
где r — расстояние от блинного проводника до точки поля.
Поле провода имеет цилиндрическую симметрию, для всех точек рамки оно будет направлено перпендикулярно. Если рассмотреть по очереди силы Ампера, которые действуют на каждый из четырех составных частей рамки, то выражение для модуля силы Ампера можно использовать в виде:
[ F=IBlsinalpha left(2.3right), ]
где ( l=а ). Надо отметить, что на стороны, которые перпендикулярны проводнику с током будут действовать силы равные по модулю и противоположные по направлению, так результирующий их вклад равен нулю. ( overrightarrow{F_{1A}} )=-( overrightarrow{F_{2A}} ).
Силы ( F_{4A} и F_{3A} ) направлены вдоль одной прямой, но в противоположные стороны. Следовательно, результирующую силу по модулю найдем как:
[ F=F_{4A}- F_{3A}left(2.4right). ]
Используя закон Ампера, и помня, что магнитное поле перпендикулярно току в сторонах квадрата, запишем:
[ F_{4A}=frac{{mu }_0}{2pi }frac{I^2}{a}, F_{3A}=frac{{mu }_0}{2pi }frac{I^2}{2a}left(2.5right). ]
Подставим (2.5) в (2.4), получим:
[ F=frac{{mu }_0}{2pi }frac{I^2}{a}- frac{{mu }_0}{2pi }frac{I^2}{2a}=frac{{mu }_0}{4pi }frac{I^2}{a}. ]
( F=frac{{mu }_0}{4pi }frac{I^2}{a}. )
Уровень9 класс ПредметФизика СложностьПростая
Однородное магнитное поле величиной двадцать Тесла удерживает от падения помещенный в него (перпендикулярно линиям магнитной индукции) прямолинейный проводник. Масса проводника четыре килограмма, длина пол метра.
Необходимо: определить силу тока в проводнике.
m=4 кг; l=0,5 м; B=20 Тл; I — ?
На прямолинейный проводник воздействуют две силы: ( F=m cdot g ) – сила тяжести и ( F=B cdot I cdot l ) – сила Ампера.
Поскольку проводник не падает – эти силы равны ( m cdot g=B cdot I cdot l ).
Из полученного равенства выведем формулу для определения силы тока в проводнике, помещенном в магнитное поле ( I=dfrac{mcdot g}{Bcdot l} )
Подставив численные значения физических величин в формулу, определим силу тока в проводнике
( I=dfrac{mcdot g}{Bcdot l}=dfrac{4cdot 9,8}{20cdot 0,5}=3.92 A )
сила тока в проводнике равна три целых девяносто две сотых Ампера ( 3.92 A ).
Уровень9 класс ПредметФизика СложностьПростая
Прямой проводник длиной (l = 20) см и массой (m = 105) г подвешен горизонтально на двух легких нитях в однородном вертикальном магнитном поле. Модуль индукции магнитного поля (В = 0,20) Тл. Если по проводнику пропустить ток (I = 5,0) А, то нити, поддерживающие проводник, отклонятся от вертикали на угол ( alpha ). Сколько градусов будет составлять угол ( alpha ).
На проводник действуют силы натяжения со стороны каждой нити ( Т_1 = Т_2 ), сила Ампера ( F_A ) и сила тяжести ( mg ). Проводник находится в равновесии, поэтому:
( 2cdot vec{T}+mcdot vec{g}+{{vec{F}}_{A}}=0 )
В проекциях на оси координат:
( 0_x: F_A = 2cdot Tcdot sin(alpha) ; 0_y: mcdot g = 2cdot Tcdot cos(alpha ) )
Решим совместно уравнения
( dfrac{{{F}_{A}}}{mcdot g}=dfrac{2cdot Tcdot sin alpha }{2cdot Tcdot cos alpha };,,,,,,dfrac{Icdot Bcdot l}{mcdot g}=tgalpha )
Уровень9 класс ПредметФизика СложностьПростая
Прямолинейный горизонтально расположенный проводник находится в однородном магнитном поле, модуль индукции которого ( В = 0,10 ) Тл.
По проводнику протекает ток ( I = 1,8 ) А, причем сила тяжести полностью уравновешивается силой, действующей на проводник со стороны поля.
Если плотность материала проводника ( ρ = 8900 ) кг/м3, то какова площадь его поперечного сечения, мм2?
Согласно условию задачи сила тяжести полностью уравновешивается силой Ампера.
Тогда
( mcdot g=Icdot Bcdot l )
( mcdot g=Icdot Bcdot dfrac{V}{S} )
( mcdot g=Icdot Bcdot dfrac{m}{rho cdot S} )
( S=dfrac{Icdot B}{rho cdot g} = dfrac{1.8 cdot 0.10}{ 8900 cdot 9.81} = 2 cdot 10^{-6} )м2
Уровень9 класс ПредметФизика СложностьПростая
Именно Амперу пришла идея о том, что комбинацией проводников и магнитных стрелок можно создать устройство, которое предаёт информацию на расстояние. Идея телеграфа возникла в первые же месяцы после открытия электромагнетизма. Однако широкое распространение электромагнитный телеграф приобрёл после того, как Самюэль Морзе создал более удобный аппарат и, главное, разработал двоичную азбуку, состоящую из точек и тире, которая так и называется «Азбука Морзе»
После открытия действия магнитного поля на проводник с током, Ампер понял, что это открытие можно использовать для того, чтобы заставить проводник двигаться в магнитном поле. Так магнетизм можно превратить в механическое движение – создать двигатель. Одним из первых, работающих на постоянном токе, был электродвигатель, созданный в 1834 г. русским электротехником Б. С. Якоби.
В 1269 г. французский естествоиспытатель Пьер Мари Кур написал труд под названием «Письмо о магните». Основной целью Пьера Мари Кура было создание вечного двигателя, в котором он собирался использовать удивительные свойства магнитов. Насколько успешными были его попытки не известно, но достоверно то, что Якоби использовал свой электродвигатель для того, чтобы привести в движение лодку, при этом ему удалось её разогнать до скорости 4,5 км/ч.
Необходимо упомянуть ещё об одном устройстве, работающем на основе законов Ампера. Ампер показал, что катушка с током ведёт себя подобно постоянному магниту, а это значит – можно сконструировать электромагнит – устройство, мощность которого можно регулировать.
Математик Гаусс, когда познакомился с исследованиями Ампера, предложил создать оригинальную пушку, работающую на принципе действия магнитного поля на железный шарик – снаряд.
Необходимо обратить внимание на то, в какую историческую эпоху были сделаны эти открытия. В первой половине XIX века Европа семимильными шагами шла по пути промышленной революции – это благодатное время для научно-исследовательских открытий и быстрого внедрения их в практику. Ампер, несомненно, внёс весомый вклад в этот процесс, дав цивилизации электромагниты, электродвигатели и телеграф, которые до сих пор находят широкое применение.
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними.
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.
Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.
Давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях.
Между любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки
Источник
