Сила работает на растяжение

Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).

Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Ещё настоятельно рекомендую взглянуть на статью:
Расчёт статистически определимого бруса
Если разберёте теорию в данной статье и задачи по ссылкам, то станете гуру в теме «Растяжение-сжатие» =)
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N, является равнодействующей внутренних усилий распределенных по поперечному сечению стержня (рис. 2, б). Исходя из определения напряжений, согласно выражению (1), можно записать для продольной силы:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Чтобы определить нормальные напряжения в любой точке бруса необходимо знать закон их распределения по поперечному сечению бруса. Экспериментальные исследования показывают: если нанести на поверхность стержня ряд взаимно перпендикулярных линий, то после приложения внешней растягивающей нагрузки поперечные линии не искривляются и остаются параллельными друг другу (рис.6, а). Об этом явлении говорит гипотеза плоских сечений (гипотеза Бернулли): сечения, плоские до деформации, остаются плоскими и после деформации.

Так как все продольные волокна стержня деформируются одинаково, то и напряжения в поперечном сечении одинаковы, а эпюра напряжений σ по высоте поперечного сечения стержня выглядит, как показано на рис.6, б. Видно, что напряжения равномерно распределены по поперечному сечению стержня, т.е. во всех точках сечения σ = const. Выражение для определения величины напряжения имеет вид:
Таким образом, нормальные напряжения, возникающие в поперечных сечениях растянутого или сжатого бруса, равны отношению продольной силы к площади его поперечного сечения. Нормальные напряжения принято считать положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов

Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.

Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Основными механическими свойствами материалов при их деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала сопротивляться воздействию внешних сил, не разрушаясь и без появления остаточных деформаций.
Пластичность – свойство материала выдерживать без разрушения большие остаточные деформации. Неисчезающие после снятия внешних нагрузок деформации называются пластическими.
Хрупкость – свойство материала разрушаться при очень малых остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость – свойство материала (тела) полностью восстанавливать свою форму и размеры после устранения причин, вызвавших деформацию.
Твердость – свойство материала сопротивляться проникновению в него других тел.
Рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Пусть круглый стержень длинной l0 и начальным постоянным поперечным сечением площади A0 статически растягивается с обоих торцов силой F.

Диаграмма сжатия стержня имеет вид (рис. 10, а)

где Δl = l — l0 абсолютное удлинение стержня; ε = Δl / l0 — относительное продольное удлинение стержня; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности (временное сопротивление); εост — остаточная деформация после снятия внешних нагрузок. Для материалов, не имеющих ярко выраженную площадку текучести, вводят условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня возникает локальное утончение его диаметра («шейка»). Дальнейшее абсолютное удлинение стержня идет в зоне шейки ( зона местной текучести). При достижении напряжением предела текучести σт глянцевая поверхность стержня становится немного матовой – на его поверхности появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.

Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Целью расчета любой конструкции является использование полученных результатов для оценки пригодности этой конструкции к эксплуатации при минимальном расходе материала, что находит отражение в методах расчета на прочность и жесткость.
Условие прочности стержня при его растяжении (сжатии):
При проектном расчете определяется площадь опасного сечения стержня:
При определении допускаемой нагрузки рассчитывается допускаемая нормальная сила:
Расчет на жесткость при растяжении и сжатии.
Работоспособность стержня определяется его предельной деформацией [ l ]. Абсолютное удлинение стержня должно удовлетворять условию:
Часто дополнительно делают расчет на жесткость отдельных участков стержня.
Следующая важная статья теории:
Изгиб балки
Источник
| С этого раздела начинается введение новых понятий, специфических для дисциплины «сопротивление материалов». Первым важным является понятие под названием внутренний силовой фактор. Частным его случаем | Рис.2.2.1 |
является понятие усилие растяжения (сжатия).
Рассмотрим рис.2.2.1. Если для среднего стержня ответ на вопрос «чему равняется усилие растяжения?» является очевидным (оно равняется F), то для верхнего стержня этот вопрос обычно вызывает затруднения (часто говорят, что оно равно нулю или 2F). Однако третий нижний рисунок равносилен первым двум, поскольку реакция R=F. Таким образом, во всех этих случаях усилие растяжения равно F , поскольку схемы равносильны.
Сила растяжения обозначается буквой N. В нашем случае
N = F
Рассмотрим теперь рис.2.2.2. Можно ли сказать, чему равна сила растяжения? Нет, т.к. это равносильно тому, что спросить: «Чему равна ширина реки Волга»? В обоих случаях, нужно указывать – в каком месте.
Рис.2.2.2
Введем следующее определение. Разделим мысленно брус на две части сечением В-В.
Продольной силой N врассматриваемом внутреннем сеченииназовем равнодействующую всех внешних осевых сил, с которой левая часть воздействует на правую часть (или с которой правая часть воздействует на левую)
Примечания.
1). Синонимами термина «продольная сила»» являются термины нормальная сила, усилие растяжения, осевая сила.
2). Главная идея сопротивления материалов заключается именно в том, что тело считается состоящим из двух частей.
Это определение можно сформулировать как следующее правило для вычисленияN: продольная сила это сумма всех внешних осевых сил, которые лежат справа или слева от сечения.
Правило знаков.
Если внешняя сила действует на сечение растягивающим образом, то она дает вклад в N со знаком «+», если действует сжимающим образом, то она делает вклад в N со знаком «-».
Для того чтобы указать, на какое сечение действует продольная сила, сечение и N снабжаются номером и индексом. Например, так, как показано на рис.2.2.3
| N1 = F — 3F N2 = — 3F |
Рис.2.2.3
При наличии внешних погонныхсил осевая сила N зависит от положения сечения более сложным образом. Рассмотрим, например, задачу вычисления продольной силы с учетом силы тяжести (рис.2.2.4). Обозначим через q погонный вес бруса (для стандартных профилей прокатной стали, погонная масса приводится в таблицах сортамента). Пусть F = 400 Н, q = 200 Н/м. Рассмотрим сечение на расстоянии s от незакрепленного конца (см. рис.2.2.3). Тогда:
N = – F – qs
Задавая разные значения для s получим разные значения N (см. таблицу).
| s(м) | ||||
| N(Н) | -400 | -600 | -800 | -1000 |
Зависимость N от положения сечения для наглядности представляют графически. График этой зависимости называется эпюрой N.
Рис.2.2.4
Правила графического изображения N.
1). Значения N откладываются перпендикулярно оси бруса.
2). Если усилие N является растягивающим, то ставится знак «+» (в нашем примере на рис.2.2.4 имеем отрицательный знак).
Метод сечений
Это метод, который позволяет определять N в сложных конструкциях типа стержневой системы, например, фермы. Суть метода рассмотрим на простом примере, приведенном на рис.2.3.1. Пусть длины стержней l1=4м, l2=5м, ВС=3м. Тогда ; .
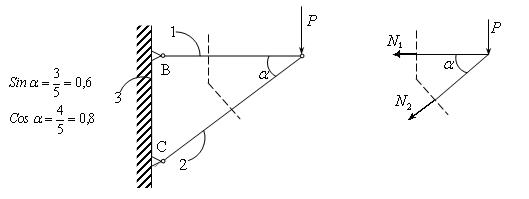
рис.2.3.1.
Найдем усилия растяжения.
Сделаем сечение, которое делит конструкцию на две части. Нарисуем правую часть. На нее левая часть действует силами .
Конструкция в целом находится в покое, следовательно, любая её часть то же находится в покое, тогда для правой части можно записать уравнения равновесия:
Отсюда, находим:
Анализ решения:
1) Видно, что первый стержень растягивается, так как N1 >0, а второй стержень сжимается, так как N2<0.
2) Чем меньше , тем меньше , следовательно, тем больше , причем, , при .
Резюмируя можно, что метод сечений заключается в следующем:
1) Конструкция делится на две части сквозным сечением.
2) В сечениях стержней изображаются внутренние силовые факторы (т.е. изображается — воздействие одной части конструкции на другую)
3) Записываются уравнения равновесия для одной из частей конструкции.
4) Проводится решение системы уравнений, и отыскиваются внутренние силовые факторы.
Источник
Определение нормальной силы
Центральное растяжение (сжатие) – одно из наиболее простых видов нагружения. Методом сечений в поперечном сечении бруса обнаруживается только один внутренний силовой фактор – нормальная сила. Ее вектор перпендикулярен к поперечному сечению и направлен вдоль продольной оси бруса. Брус, работающий на растяжение-сжатие, принято называть стержнем.
Согласно методу сечений величина и направление продольной силы определяются из уравнения равновесия, составленного для отсеченной части бруса:
(2.9)
Таким образом, продольная (нормальная) сила о произвольном сечении бруса численно равна алгебраической сулеме проекций па продольную ось всех внешних (активных и реактивных) сил, приложенных к отсеченной части.
В общем случае
(2.10)
где – интенсивность нагрузки, распределенной вдоль оси бруса на участке от 0 до .
Продольная сила считается положительной, если она вызывает растяжение, т.е. направлена от сечения. В поперечном сечении бруса она является равнодействующей внутренних нормальных сил, возникающих в этом сечении.
График функции называется эпюрой нормальных сил. Из выражения (2.10) следует, что
(2.11)
т.е. интенсивность распределенной нагрузки в каждом сечении равна по величине и знаку тангенсу угла наклона касательной к эпюре в соответствующей рассматриваемому сечению точке эпюры.
Нормальные напряжения и деформации
При растяжении (сжатии) бруса в поперечных сечениях возникают только нормальные напряжения. Чтобы задача определения по известным N А имела единственное решение, необходимо установить закон распределения σ(x) по сечению. Для этого используется гипотеза плоских сечений (гипотеза Бернулли): сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к его оси и при деформации. Поперечные сечения лишь перемещаются вдоль оси, оставаясь параллельными друг другу.
Допустим, брус состоит из бесконечно большого числа продольных волокон. Из гипотезы Бернулли следует, что все волокна деформируются одинаково. Поскольку, согласно закону Гука, равным деформациям соответствуют равные напряжения, то при растяжении (сжатии) бруса нормальные напряжения равномерно распределяются по поперечному сечению, т.е.;.
Как известно,. Так как, то . Отсюда
(2.12)
Положительными считаются направления , соответствующие растяжению.
В сечениях бруса, примыкающих к месту приложения внешних сил и к закреплениям, распределение напряжений зависит
Рис. 2.7
от способа приложения нагрузки и может быть неравномерным. Поэтому гипотеза плоских сечений в этих местах неверна.
Рассмотрим однородное напряженное состояние бруса, когда напряжения не изменяются по длине (рис. 2.7).
Изменение линейных размеров называется абсолютным удлинением; отношение – относительным удлинением или линейной деформацией.
В случае неоднородного напряженного состояния линейная деформация определяется выражением , где – приращение отрезка .
Между линейными деформациями и вызывающими их напряжениями существует связь, обусловленная упругими свойствами материала. Эта связь определяется законом Гука:
(2.13)
где Е – модуль упругости материала.
Рассмотрим выражение. Согласно формуле (2.13) получим; поскольку
Отсюда изменение длины всего бруса
(2.14)
Произведение НА называется жесткостью бруса при растяжении (сжатии).
Если законы изменения N и А различны для отдельных участков бруса, то
(2.15)
где – число участков.
В частном случае, когда N и А постоянны по длине бруса, получаем формулу Гука в виде
(2.16)
Итак, перемещение i-го сечения с координатой х относительно неподвижного сечения
(2.17)
Аналогично можно записать
(2.18)
где – перемещение начального сечения относительно заделки.
Пусть сечение бруса (см. рис. 2.7) имеет форму прямоугольника со сторонами а и b, тогда при растяжении бруса периметр его уменьшится. Величина характеризует относительное изменение периметра поперечного сечения и называется поперечной деформацией. Если сечение круглое, то . Отношение поперечной деформации к линейной величине постоянно для данного материала и называется коэффициентом Пуассона:
(2.19)
Для стали и большинства металлических материалов . В общем случае .
Источник
Растяжение и сжатие – это такой способ действия внешних сил, при котором в поперечных сечениях элементов конструкций возникает лишь один внутренний силовой фактор – продольная сила N. На растяжения (сжатие) работают многие строительные конструкции и детали машин. Например, элементы металлоконструкций: стойки, колонны, стержни ферменных конструкций и т.д. Это первый вид деформации, с которым знакомится будущий инженер. Впервые знакомится с понятиями: внутреннее усилие, напряжение, деформация и перемещение. В рамках этого раздела изучается диаграмма растяжения (сжатия), рассматриваются основные механические характеристики материалов, которые в дальнейшем используются в расчетах на прочность и жесткость.
Как определить удлинение (укорочение) стержня (бруса) ?
В данной статье будем разбираться, как определить удлинение или укорочение стержня (бруса) под действием внешней нагрузки. Будем разбираться сразу на примерах. Пример расчета удлинения бруса Возьмем брус круглого и постоянного поперечного сечения, который нагружен…
Как определить нормальное напряжение?
Сегодня будем говорить о том, как определить нормальное напряжение при растяжении (сжатии). Долго говорить не придется, так как определяется оно элементарно. Формула для нахождения нормального напряжения следующая: То есть это отношение продольной силы (N)…
Статически неопределимая стержневая система. Задача №14
Абсолютно жесткая балка, закреплённая с помощью шарнира и пары вертикальных стрежней, нагруженная силой P. Выяснить какие продольные усилия возникают в стержнях. Произвести прочностной расчет.
Принцип независимости действия сил
Принцип независимости действия сил, также именуемые как принцип суперпозиции, занимает важное место в сопромате. Благодаря этому принципу возможно решение многих линейных задач.
Перемещения при растяжении (сжатии)
Определение перемещений (деформаций) является важной задачей. По величине абсолютного перемещения можно судить о жесткости конструкции. Этот параметр является неотъемлемой частью любого инженерного расчета. Студенты, как правило, оттачивают полученные теоретические знания на практике по разделу…
Эпюра продольных сил — как построить?
В этой статье пойдет речь о том, как строятся эпюры продольных сил, какой метод используется при вычислении продольных сил. Также в статье будут разобраны примеры построения эпюр при различных видах нагрузок. Пример построения эпюры продольных…
Как определить продольную силу?
Решение практически любой задачи на растяжение (сжатие) начинается с определения продольных сил. Зная их величину можно определить такие важные параметры как напряжение или перемещение. Как говорилось ранее, при чистом растяжении (сжатии) возникает лишь один внутренний…
Диаграмма растяжения (сжатия): предел пропорциональности, упругости, текучести и прочности
При испытании образцов на растяжение (сжатие) определяются такие характеристики как модуль упругости, коэффициент Пуассона, предел текучести, временное сопротивление и другие. Эти величины в дальнейшем используются при прочностных расчетах, расчетах на жесткость и устойчивость. Испытание…
Монтажные напряжения — как определить?
Иногда так бывает, что при монтаже какой-то конструкции выясняется, что детали, из которых она состоит, не стыкуются между собой. Но иногда эти не точности можно компенсировать и собрать конструкцию за счет приложения какой-то силы….
Источник
