Решение задач на растяжение пружины

Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
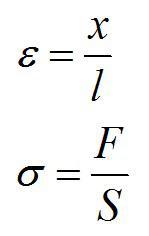
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
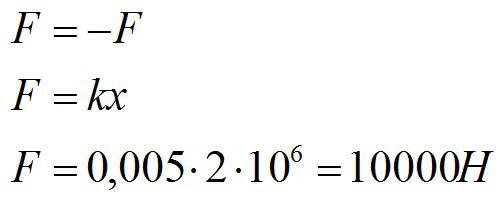
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
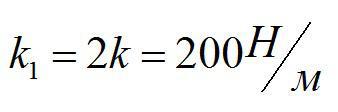
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
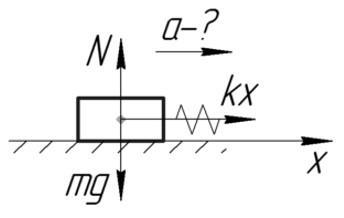
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
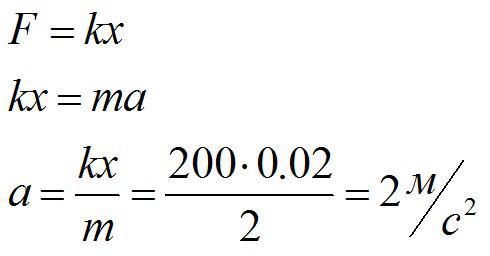
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
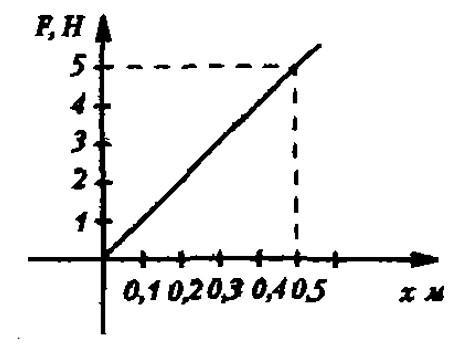
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
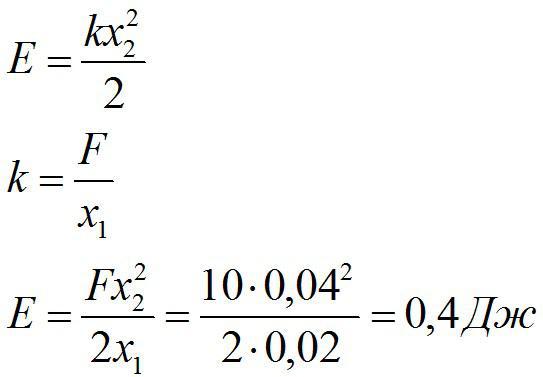
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Автор
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
Подробности
Просмотров: 899
«Физика — 10 класс»
При решении задач по этой теме надо иметь в виду, что закон Гука справедлив только при упругих деформациях тел. Сила упругости не зависит от того, какая происходит деформация: сжатия или растяжения, она одинакова при одинаковых Δl. Кроме этого, считается, что сила упругости вдоль всей пружины одинакова, так как масса пружины обычно не учитывается.
Задача 1.
При помощи пружинного динамометра поднимают с ускорением а = 2,5 м/с2, направленным вверх, груз массой m = 2 кг. Определите модуль удлинения пружины динамометра, если её жёсткость k = 1000 Н/м.

Р е ш е н и е.
Согласно закону Гука, выражающему связь между модулем внешней силы , вызывающей растяжение пружины, и её удлинением, имеем F = kΔl. Отсюда
Для нахождения силы воспользуемся вторым законом Ньютона. На груз, кроме силы тяжести m, действует сила упругости пружины, равная по модулю F и направленная вертикально вверх. Согласно второму закону Ньютона m = F + m.
Направим ось OY вертикально вверх так, чтобы пружина была расположена вдоль этой оси (рис. 3.16). В проекции на ось OY второй закон Ньютона можно записать в виде mау = Fy + mgy
Так как ау = a, gy = -g и Fy = F, то F = mа + mg = m(а + g).
Следовательно,
Задача 2.
Определите, как изменяется сила натяжения пружины, прикреплённой к бруску массой m = 5 кг, находящемуся неподвижно на наклонной поверхности, при изменении угла наклона от 30° до 60°. Трение не учитывайте.

Р е ш е н и е.
На брусок действуют сила тяжести, сила натяжения пружины и сила реакции опоры (рис. 3.17).
Условие равновесия бруска: m + + yпp = 0.
Запишем это условие в проекциях на оси ОХ и OY:
Из первого уравнения системы получим Fyпp = mg sinα.
При изменении угла наклона изменение силы упругости найдём из выражения ΔFyпp = mg(sinα2 — sinα1) = 5 • 10 • (0,866 — 0,5) (Н) = 18,3 Н.
Задача 3.
К потолку подвешены последовательно две невесомые пружины жёсткостями 60 Н/м и 40 Н/м. К нижнему концу второй пружины прикреплён груз массой 0,1 кг. Определите жёсткость воображаемой пружины, удлинение которой было бы таким же, как и двух пружин при подвешивании к ней такого же груза (эффективную жёсткость).

Р е ш е н и е.
Так как весом пружин можно пренебречь, то очевидно, что силы натяжения пружин равны (рис. 3.18). Тогда согласно закону Гука
Fynp1 = Fупр2; k1x1 = k2х2. (1)
На подвешенный груз действуют две силы — сила тяжести и сила натяжения второй пружины.
Условие равновесия груза запишем в виде mg = k2х2.
Из этого уравнения найдём удлинение
Подставив выражение для х2 в уравнение (1), получим для удлинения
Определим теперь эффективную жёсткость. Запишем закон Гука для воображаемой пружины:
Подставив в формулу (2) выражения для удлинений x1 и х2 пружин, получим
Для эффективной жёсткости получим выражение
Задача 4.
Через блок, закреплённый у края стола, перекинута нерастяжимая нить, к концам которой привязаны брусок массой m1 = 1 кг, находящийся на горизонтальной поверхности стола, и пружина жёсткостью k = 50 Н/м, расположенная вертикально. Ко второму концу пружины привязана гиря массой m2 = 200 г (рис. 3.19). Определите удлинение пружины при движении тел. Силу трения, массы пружины, блока и нити не учитывайте.

Р е ш е н и е.
На брусок действуют сила тяжести, сила реакции опоры и сила натяжения нити.
На гирю действуют сила тяжести и сила натяжения пружины.
Согласно второму закону Ньютона для бруска и гири запишем:
m11 = m1 + + ;
m22 = m + упр.
В проекциях на выбранные оси координат запишем: на ось ОХ: m1а1 = Т;
на ось OY:
Так как нить нерастяжима, то модули ускорений равны: а1 = а2 = а.
В силу условия малых масс пружины, нити и блока можно записать: T2 = Fупр и Т1 = Т2 = Т.
Учтя последние равенства, систему уравнений (1) запишем в виде
Выразив ускорение из первого уравнения системы и подставив его во второе, получим
Из этого уравнения найдём силу натяжения нити:
Так как согласно закону Гука Fупр = kx, то
Тогда удлинение пружины
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Динамика — Физика, учебник для 10 класса — Класс!ная физика
Основное утверждение механики —
Сила —
Инертность тела. Масса. Единица массы —
Первый закон Ньютона —
Второй закон Ньютона —
Принцип суперпозиции сил —
Примеры решения задач по теме «Второй закон Ньютона» —
Третий закон Ньютона —
Геоцентрическая система отсчёта —
Принцип относительности Галилея. Инвариантные и относительные величины —
Силы в природе —
Сила тяжести и сила всемирного тяготения —
Сила тяжести на других планетах —
Примеры решения задач по теме «Закон всемирного тяготения» —
Первая космическая скорость —
Примеры решения задач по теме «Первая космическая скорость» —
Вес. Невесомость —
Деформация и силы упругости. Закон Гука —
Примеры решения задач по теме «Силы упругости. Закон Гука» —
Силы трения —
Примеры решения задач по теме «Силы трения» —
Примеры решения задач по теме «Силы трения» (продолжение) —
Источник
В этой статье собраны задачи, в которых так или иначе присутствует сила упругости. Задачи прошлых лет ЕГЭ или из олимпиадных подборок.
Задача 1. Две невесомые пружины прикреплены к верхнему и нижнему торцам неподвижного цилиндра. Концы пружин соединены. Жесткость верхней пружины равна Н/м, жесткость нижней Н/м. Пружины находятся в нерастянутом состоянии. Между ними вставили тонкую платформу массой кг. Пружины прикрепляют к платформе (см. рис.). На сколько при этом растянулась верхняя пружина?

К задаче 1
Запишем уравнение по второму закону Ньютона для груза:
Здесь – сила упругости верхней пружины, она пытается вернуться в нерастянутое состояние, поэтому будет тянуть платформу вверх. – сила упругости нижней пружины, она пытается вернуться в нерастянутое состояние, поэтому будет толкать платформу вверх.
Тогда
При этом на сколько растянулась верхняя пружина, на столько же сжалась нижняя: . Следовательно,
Ответ: 40 см.
Задача 2. К потолку прикреплена конструкция, состоящая из двух пружин и двух маленьких чашек A и B. Расстояние от пола до потолка равно 2 м. Жесткости пружин равны Н/м и Н/м. Длины нерастянутых пружин одинаковы и равны 30 см. Масса чашки A равна г, чашка B невесома. Груз какой массы надо положить в чашку A, чтобы чашка B достала до пола? Какой груз надо положить в чашку B, чтобы она достала до пола (чашка A при этом пуста)?

К задаче 2
Чтобы чашка В достала до пола, нужно, чтобы первая пружина растянулась до длины 1,7 м – тогда нерастянутая вторая пружина длиной 30 см коснется пола. Тогда удлинение пружины А должно составить 1 м 40 см. Следовательно,
Но сама чаша весит 100 г, следовательно, добавив 2 кг в чашу, мы обеспечим нужную силу.
Система из двух пружинок, соединенныx последовательно, имеет жесткость
Растягивать всю систему будем на 1,4 м – именно столько чашку В отделяет от пола.
Так как чашка А весит 100 г, то в этом случае масса дополнительного груза будет 1,3 кг.
Ответ: а) 2 кг; б)1,3 кг.
Задача 3. Два шарика подвешены на вертикальных тонких нитях так, что они находятся на одной высоте. Между ними находится сжатая и связанная нитью пружина. При пережигании связывающей нити пружина распрямляется, отклоняя шарики в разные стороны на одинаковые углы. Во сколько раз одна нить длиннее другой, если отношение масс ? Считать величину сжатия пружины во много раз меньше длин нитей.

К задаче 3
Когда пружина толкнет шарики, они начнут двигаться по окружностям радиусов и соответственно. Первый поднимется при этом на высоту , а второй – на высоту . Определим эти высоты:
По закону сохранения импульса
Возведем в квадрат:
Или
Из равенства кинетической и потенциальной энергий следует, что
И аналогично
Поэтому
Подставим выражения, полученные вначале:
Сократим:
Ответ: .
Задача 4. Брусок, покоящийся на горизонтальном столе, и пружинный маятник, состоящий из грузика и легкой пружины, связаны легкой нерастяжимой нитью через идеальный блок (см. рисунок). Коэффициент трения между основанием бруска и поверхностью стола равен 0,25. Груз маятника совершает колебания с периодом 0,5 с вдоль вертикали, совпадающей с вертикальным отрезком нити. Максимально возможная амплитуда этих колебаний, при которой они остаются гармоническими, равна 4 см. Чему равно отношение массы бруска к массе грузика?

К задаче 4
Координата грузика при колебаниях может быть записана как
Запишем второй закон Ньютона для грузика:
Запишем второй закон Ньютона для бруска:
Сила трения скольжения равна
Тогда, чтобы брусок не поехал под действием качаний грузика, нужно, чтобы соблюдалось условие:
Откуда отношение масс равно
Определить ускорение можно, взяв вторую производную по координате:
Максимальное ускорение равно
Подставим это ускорение в полученное отношение масс:
Ответ:
Задача 5. Пружинное ружьё наклонено под углом к горизонту. Энергия сжатой пружины равна 0,41 Дж. При выстреле шарик массой г проходит по стволу ружья расстояние , вылетает и падает на расстоянии м от дула ружья в точку , находящуюся с ним на одной высоте (см. рис.). Найдите расстояние . Трением в стволе и сопротивлением воздуха пренебречь.

К задаче 5
Определим скорость шарика при вылете из ружья .
По горизонтали шарик полетит равномерно со скоростью :
По вертикали шарик будет иметь начальную скорость , и она станет равной нулю в максимальной точке подъема:
Тогда время полета до максимальной точки подъема
Откуда скорость равна
Определим скорость шарика вначале. Вся энергия пружины переходит в кинетическую энергию шарика:
Таким образом, в начале трубы скорость была 4,05, а в конце – 3,4 м/с. Составим закон сохранения энергии. Учтем, что конец трубы приподнят относительно начала, следовательно, часть энергии шарика превратилась в потенциальную:
Откуда
Тогда длина ствола больше вдвое, так как катет, лежащий против угла в тридцать градусов, вдвое короче гипотенузы. .
Ответ: 48 см.
Источник
В 1635 году родился Роберт Гук, английский физик, член Лондонского
королевского общества, его секретарь. В 1660 году открыл закон упругости для
твердых тел (закон Гука).
В курсе 7 класса одной из сложных тем является условие равновесия груза на
пружине: kx=mg, но предварительно для более эффективного понимания этой темы
проводится эксперимент по закону Гука, а затем комментируются формулы: Fу=kx и
Fт=mg .
Задачи на данную тему
1) Какова жесткость пружины , если груз массой 10 кг растягивает пружину на
10 см.
Ответ
: 1000Н/м
2) Используя полученный Ответет из предыдущей задачи определите какой
груз нужно подвесить к пружине , чтобы растянуть ее на 20 см.
Ответ
: 20 кг.
3) Груз массой 3 кг растягивает пружину на 5 см . Каким должен быть груз ,
который растянет пружину на 8см.
Ответ
: 4,8 кг.
Фрагмент урока
Приложение 1
III. Изучение нового материала:
Вам уже известно, что на все тела, находящиеся на Земле, действует сила
тяжести. В результате действия силы тяжести на Землю падает подброшенный камень,
выпущенная из лука стрела, снежинки.
Почему же покоятся тела, подвешенные на нити или лежащие на опоре?
По-видимому, сила тяжести уравновешивается какой-то другой силой. Что это за
сила и как она возникает.
Проведем опыт: на упругий подвес поместим гирю. Под действием силы
тяжести гиря начнет двигаться вниз, и подвес деформируется – его длина
увеличится. При этом возникнет сила, с которой подвес действует на тело. Когда
эта сила уравновесит силу тяжести, тело остановится. Из этого опыта можно
сделать вывод, что на гирю, кроме силы тяжести, направленной вертикально вниз,
действует другая сила. Эта сила направлена вертикально вверх. Она и
уравновешивает силу тяжести. Эту силу называют силой упругости.
Аналогичные явления происходят с любым телом которое мы положили на опору.
Ребята, запишите, пожалуйста, в тетрадях определение силы упругости: Сила,
возникающая в теле в результате его деформации, и стремящаяся вернуть тело в
исходное положение называется силой упругости.
– Проведем эксперимент: линейка и пружина с указателем закреплены на
штативе. Будем поочередно подвешивать грузы на пружину и фиксировать ее
удлинение. Заносим данные в таблицу . Для расчета силы упругости используем
равенство сил, действующих на груз: Fупр = Fтяж = mg. По данным таблицы строим
график зависимости Fупр(∆l).
Вопросы учащимся:
– Какую линию получили на графике?
– Как называется такая зависимость в математике?
– Что происходит с силой упругости, если длина пружины увеличивается?
Уменьшается?
– Как изменится сила упругости, если длина пружины увеличится в 2 раза?
Посмотрим на график.
– Найдем отношение силы упругости к удлинению пружины (первый результат
считаю я, остальные вы – по вариантам):
∆F1/∆l1= ∆F2/∆l2=
∆F3/∆l3= ∆F4/∆l4=
– Какой вывод можно сделать об отношении силы упругости к удлинению пружины?
– Мы с вами получили закон, открытый английским физиком Робертом Гуком в
1660г.
– Закон Гука: Fупр = k∆l – сила упругости прямо пропорциональна
величине деформации. Обсудим формулу закона и попытаемся определить, какие
величины в нее входят (обсуждение формулы, записи величин и единиц их
измерения).
Теперь мы можем написать условие равновесия груза на пружине : mg = k∆l ,
используем это условие при решении задачи №1:
1) Какова жесткость пружины , если груз массой 10 кг растягивает пружину на
0,1 м.
Дано: М=10кг
L=0,1м
k-?Решение: mg = k∆l
mg : ∆l = k
После подстановки получаем ответ: 1000Н/м
Теперь зная жесткость пружины, разберем ситуацию каким образом мы можем
узнать массу тела, рассмотрим задачу №2:
2) Используя полученный ответ из предыдущей задачи определите какой груз
нужно подвесить к пружине, чтобы растянуть ее на 20 см.
Дано: k =1000Н/м
L=0,2м
М – ?Решение: mg = k ∆l
m = k ∆l:g
После подстановки получаем ответ: 20 кг
А теперь используем наши умения и навыки для решения более сложной задачи:
3) Груз массой 3 кг растягивает пружину на 5 см. Каким должен быть груз,
который растянет пружину на 8см.
Дано: М1=3кг
L1=0,05м
L2=0,08м
М2=?Решение: М1 g = k L1
М1 g : L1 = k =600 Н/м
Нашли жесткость, теперь можем написать условие равновесия груза на пружине и
найти массу груза:
М2 g = k∆l , М2=k L2: g=4,8 кг,
Ответ: 4,8 кг
Источник
